当前位置：文档之家 › 自动控制理论-控制系统的校正与设计

自动控制理论-控制系统的校正与设计

  • 格式：ppt
  • 大小：3.94 MB
  • 文档页数：67

下载文档原格式

  / 67

合集下载

自动控制理论课程设计——超前校正环节的设计

自动控制理论课程设计——超前校正环节的设计

超前校正环节的设计一， 设计课题已知单位反馈系统开环传递函数如下：()()()10.110.3O kG s s s s =++试设计超前校正环节，使其校正后系统的静态速度误差系数6v K ≤，相角裕度为45度，并绘制校正前后系统的单位阶跃响应曲线，开环Bode 图和闭环Nyquist 图。

二、课程设计目的1. 通过课程设计使学生更进一步掌握自动控制原理课程的有关知识，加深对内涵的理解，提高解决实际问题的能力。

2. 理解自动控制原理中的关于开环传递函数，闭环传递函数的概念以及二者之间的区别和联系。

3. 理解在自动控制系统中对不同的系统选用不同的校正方式，以保证得到最佳的系统。

4. 理解在校正过程中的静态速度误差系数，相角裕度，截止频率，超前(滞后)角频率，分度系数，时间常数等参数。

5. 学习MATLAB 在自动控制中的应用，会利用MA TLAB 提供的函数求出所需要得到的实验结果。

6. 从总体上把握对系统进行校正的思路，能够将理论操作联系实际、运用于实际。

三、课程设计思想我选择的题目是超前校正环节的设计，通过参考课本和课外书，我大体按以下思路进行设计。

首先通过编写程序显示校正前的开环Bode 图，单位阶跃响应曲线和闭环Nyquist 图。

在Bode 图上找出剪切频率，算出相角裕量。

然后根据设计要求求出使相角裕量等于45度的新的剪切频率和分度系数a 。

最后通过程序显示校正后的Bode 图，阶跃响应曲线和Nyquist 图，并验证其是否符合要求。

四、课程设计的步骤及结果 1、因为()()()10.110.3O k G s s s s =++是Ⅰ型系统，其静态速度误差系数Kv=K,因为题目要求校正后系统的静态速度误差系数6v K ≤，所以取K=6。

通过以下程序画出未校正系统的开环Bode 图，单位阶跃响应曲线和闭环Nyquist 图： k=6;n1=1;d1=conv(conv([1 0],[0.1 1]),[0.3 1]); [mag,phase,w]=bode(k*n1,d1); figure(1);margin(mag,phase,w); hold on;figure(2)s1=tf(k*n1,d1); sys=feedback(s1,1); step(sys); figure(3);sys1=s1/(1+s1) nyquist(sys1); grid on; 结果如下：M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/sec)图1--校正前开环BODE 图由校正前Bode 图可以得出其剪切频率为 3.74，可以求出其相角裕量0γ=1800-900-arctan 0c ω=21.20370。

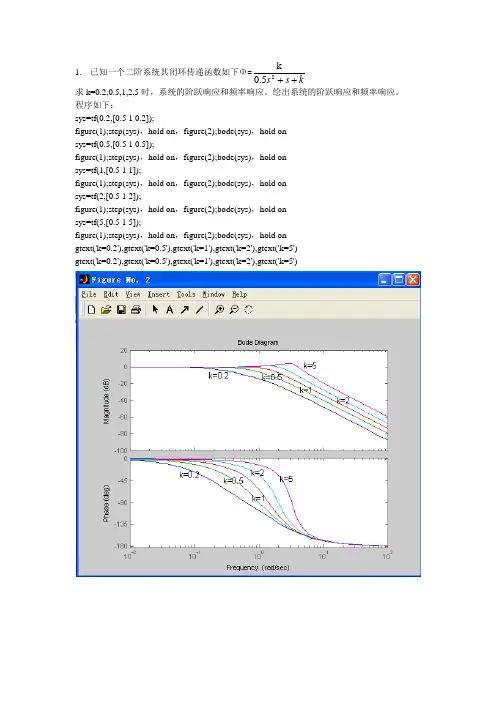
自动控制原理课程设计关于系统校正

自动控制原理课程设计关于系统校正

1. 已知一个二阶系统其闭环传递函数如下Φ=ks s ++25.0k求k=0.2,0.5,1,2,5时，系统的阶跃响应和频率响应。

绘出系统的阶跃响应和频率响应。

程序如下：sys=tf(0.2,[0.5 1 0.2]);figure(1);step(sys)，hold on ，figure(2);bode(sys)，hold on sys=tf(0.5,[0.5 1 0.5]);figure(1);step(sys)，hold on ，figure(2);bode(sys)，hold on sys=tf(1,[0.5 1 1]);figure(1);step(sys)，hold on ，figure(2);bode(sys)，hold on sys=tf(2,[0.5 1 2]);figure(1);step(sys)，hold on ，figure(2);bode(sys)，hold on sys=tf(5,[0.5 1 5]);figure(1);step(sys)，hold on ，figure(2);bode(sys)，hold on gtext('k=0.2'),gtext('k=0.5'),gtext('k=1'),gtext('k=2'),gtext('k=5') gtext('k=0.2'),gtext('k=0.5'),gtext('k=1'),gtext('k=2'),gtext('k=5')2.被控对象传递函数为)20030()(2++=s s s Ks G设计超前校正环节，使系统性能指标得到满足如下要求： 1） 速度误差常数=10 2） γ=45°由速度误差常数=10，k v =10=)20030(lim 2++→s s s ksx , 得k=2000程序如下：num=[2000];den=[1,30,200,0];g0=tf(num,den);figure(1);margin(g0);hold on figure(2);sys=feedback(g0,1);step(sys); w=0.1:0.1:2000;[gm,pm,wcg,wcp]=margin(g0);[mag,phase]=bode(g0,w);magdb=20*log10(mag);phim1=45;data=18;phim=phim1-pm+data;alpha=(1+sin(phim*pi/180))/(1-sin(phim*pi/180));n=find(magdb+10*log10(alpha)<=0.0001);wc=w(n(1));w1=wc/sqrt(alpha);w2=wc*sqrt(alpha);numc=[1/w1,1];denc=[1/w2,1];gc=tf(numc,denc);g=gc*g0;[gmc,pmc,wcgc,wcpc]=margin(g);gmcdb=20*log10(gmc);disp('校正装置传递函数和校正后系统开环传递函数'),gc,g, disp('校正系统的频域性能指标KG,V,WC'),[gmc,pmc,wcpc], disp('校正装置的参数T和a值:'),t=1/w1;[t,alpha],bode(g0,g);hold on,margin(g)>> 校正装置传递函数和校正后系统开环传递函数Transfer function:0.1647 s + 1-------------0.05404 s + 1Transfer function:329.4 s + 2000-------------------------------------------0.05404 s^4 + 2.621 s^3 + 40.81 s^2 + 200 s校正系统的频域性能指标KG,V,WCans =3.4126 45.8576 10.5873校正装置的参数T 和a 值:ans =0.1647 3.0472 >>3.被控对象传递函数为 )5()(+=s s K s G设计滞后校正环节，使系统性能指标满足如下要求： 1）单位斜坡稳态误差小于5% 2）闭环阻尼比ζ=0.707，ωn =1.5 rad/s 由单位斜坡稳态误差小于5%，ε=vk 1=5%，得v k =20，又由v k =)5(lim 0+→s s k sx ，得k=100.由闭环阻尼比ζ=0.707，ωn =1.5 rad/s ，可算出相角裕度ν=65.5°，穿越频率c w =0.965 程序如下：num=100;den=[1,5,0]; go=tf(num,den);margin(go);gammao=65.5;delta=6;gamma=gammao+delta; w=0.01:0.01:1000;[mag,phase]=bode(go,w); n=find(180+phase-gamma<=0.1);wgamma=w(n(1)); [mag,phase]=bode(go,wgamma); lhc=20*log10(mag);beta=10^(lhc/20); w2=wgamma/10; w1=w2/beta;numc=[1/w2,1];denc=[1/w1,1];gc=tf(numc,denc) g=go*gcbode(go,g),hold on,margin(g),betaTransfer function: 5.988 s + 1 ----------- 68.02 s + 1Transfer function: 598.8 s + 100 ---------------------------68.02 s^3 + 341.1 s^2 + 5 s beta =11.3592 >>4.设已知单位负反馈系统其开环传递函数为())1025.0)(11.0(s ++=s s s kG要求系统具有的性能指标是：1 ) 控制输入为单位速度信号（T RAD/S ）时，其稳态误差E<0.1RAD2 ） 控制输入为单位阶跃信号时，其超调量σ<35%,调整时间s t <10秒3 ） 控制输入为单位阶跃信号时，其超调量σ<25%,调整时间s t <4秒由1），可求出6.67<k<10，取k=10.2) 由题意σ=0.16+0.4（vsin 1-1）<0.35，ts=)1)sinv12.5(）1- sinv1（5.12(2-++cw pi =10,得相角裕度v=42.68°，穿越频率w c =1.027程序如下：num=10;den=[0.0625,0.625,1,0];go=tf(num,den);margin(go); gammao=42.68;delta=6;gamma=gammao+delta; w=0.01:0.01:1000;[mag,phase]=bode(go,w);n=find(180+phase-gamma<=0.1);wgamma=w(n(1)); [mag,phase]=bode(go,wgamma);lhc=20*log10(mag);beta=10^(lhc/20); w2=wgamma/10;w1=w2/beta;numc=[1/w2,1];denc=[1/w1,1];gc=tf(numc,denc) g=go*gcbode(go,g),hold on,margin(g),betaTransfer function: 7.874 s + 1 ----------- 51.69 s + 1Transfer function:78.74 s + 10 -------------------------------------3.231 s^4 + 32.37 s^3 + 52.32 s^2 + sbeta =6.5649>>未校正系统参数：20LGKG ,WC,ans =0.0000 4.0000 0.0000 3 )由题意σ=0.16+0.4（vsin 1-1）<0.25，ts=)1)sinv12.5(）1- sinv1（5.12(2-++cw pi =4,得相角裕度v=54.72°，穿越频率w c =1.935程序如下：num=10;den=[0.0625,0.625,1,0];go=tf(num,den); [kg,gamma,wg,wc]=margin(go);kgdb=20*log10(kg); w=0.001:0.001:100;[mag,phase]=bode(go,w);disp('未校正系统参数：20LGKG ,WC,');[kgdb,wc,gamma], gamma1=54.72;delta=10;phim=gamma1-gamma+delta; alpha=(1+sin(phim*pi/180))/(1-sin(phim*pi/180)); wcc=2;w3=wcc/sqrt(alpha);w4=sqrt(alpha)*wcc; numc1=[1/w3,1];denc1=[1/w4,1]; gc1=tf(numc1,denc1); go1=go*gc1;[mag1,phase1]=bode(go1,wc); lhc=20*log10(mag1); beta=10^(lhc/20);w2=wcc/10;w1=w2/beta;numc2=[1/w2,1];denc2=[1/w1,1]; gc2=tf(numc2,denc2);gc=gc1*gc2; g=gc*go;[gmc,pmc,wcgc,wcpc]=margin(g);gmcdb=20*log10(gmc);disp('超前校正部分的传递函数'),gc1,disp('滞后校正部分的传递函数'),gc2,disp('串联超前—滞后校正传递函数'),gc,disp('校正后整个系统的传递函数'),gdisp('校正后系统参数：20LGKG,WC,R及A值'),[gmcdb,wcgc,pmc,alpha], bode(go,g)超前校正部分的传递函数Transfer function:2.23 s + 1------------0.1121 s + 1滞后校正部分的传递函数Transfer function:5 s + 1-----------40.94 s + 1串联超前—滞后校正传递函数Transfer function:11.15 s^2 + 7.23 s + 1-----------------------4.591 s^2 + 41.05 s + 1校正后整个系统的传递函数Transfer function:111.5 s^2 + 72.3 s + 10--------------------------------------------------0.2869 s^5 + 5.435 s^4 + 30.31 s^3 + 41.68 s^2 + s校正后系统参数：20LGKG,WC,R及A值ans =12.5232 9.7114 56.8774 19.8837>>5.试验小结通过试验知道，模拟试验与数字试验的差距较大，在最后一个滞后—超前校正中，如果用find()函数找穿越频率则为4左右，而模拟试验时，我算出来的穿越频率为2，如果用find的函数找穿越频率则最后算出来的校正系统与模拟时的相差叫大，而直接通过计算带穿越频率为2进行试验，则与模拟试验的结果基本一致。

自动控制原理--常用校正方式及基本控制规律

自动控制原理--常用校正方式及基本控制规律

PID -- Proportional-Integral-Derivative 比例-积分-微分
P – 反映误差信号的瞬时值大小，改变快速性；
I – 反映误差信号的累计值，改变准确性；
D – 反映误差信号的变化趋势，改变平稳性。
(1) 比例(P)控制规律
R(s) E(s)
M(s)
Gc (s) K p m(t) K pe(t)
复合控制的基本原理：实质上，复合控制是一种按不 变性原理进行控制的方式。不变性原理是指在任何输入下， 均保证系统输出与作用在系统上的扰动完全无关，使系统 输出完全复现输入。
复合校正的基本思想：对提高稳态精度与改善动态性 能这两部分分别进行综合。根据动态性能要求综合反馈控 制部分，根据稳态精度要求综合顺控补偿部分，然后进行 校验和修改，直到获得满意的结果。这就是复合控制系统 综合校正的分离原则。
能。
13
(4) 比例-积分-微分(PID)控制规律
R(s)
E(s) B(s)
K
p
(1
Td
s
1 Ti s
)
M(s)
图 6-6 PID控制器
m(t)
K
pe(t)
Kp Ti
t
e( )d
0
K pTd
de(t) dt
Gc (s)
K p (1 Td s
1 Ti s
)
Kp Ti
(T1s
1)(T2s 1) s
图 6-34 按输入补偿的复合控制系统
实现输出完全复现输入(即Cr(s)=R(s))的全补偿条件
Gr
(s)
1 G0 (s)
➢按不变性原理求得的动态全补偿条件，往往难于实
现。通常，只能实现静态(稳态)全补偿或部分补偿。

自动控制原理-控制系统的校正

自动控制原理-控制系统的校正

自动控制原理
第6章 控制系统的校正
1. 基于根轨迹法的超前校正
当系统的性能指标为时域指标时，用根轨迹
法设计校正装置比较方便。
应用根轨迹法设计校正装置的基本思路是： 认为经校正后的闭环控制系统具有一对主导共轭 复数极点，系统的暂态响应主要由这一对主导极 点的位置所决定。
明，网络在正弦信号作用
下的稳态输出电压，在相 位上超前于输入。这也就
m
T
1
是所谓超前网络名称的由
来。
m
arcsin1 1
Lc
(m
)
10
lg
1
自动控制原理
在对数幅频特性中，截 止频率附近的斜率为– 40dB/dec，并且所占频率范 围较宽，此系统的动态响应 振荡强烈，平稳性很差。对 照相频曲线可明显看出，在 范围内，对–π线负穿越一次， 故系统不稳定。
一般来说，串联校正设计比反馈校正设计简 单，也比较容易对信号进行各种必要形式的变换。
反馈校正所需元件数目比串联校正少。反馈 校正可消除系统原来部分参数波动对系统性能的 影响。在性能指标要求较高的控制系统设计中， 常常兼用串联校正与反馈校正两种方式。
自动控制原理
6.1.5 基本控制规律
1. 比例控制规律(P)
虚线表示超前网络的对 数频率特性。加入超前网络 后会有增益损失，不利于稳 态精度，但可以通过提高开 环增益给予补偿。
第6章 控制系统的校正
自动控制原理
第6章 控制系统的校正
由于超前网络对数幅频特性在1/T至1/αT之间 具有正斜率，所以原系统中频段的斜率由– 40dB/dec变成了－20dB/dec，增加平稳性；还是由 于这个正斜率，使系统的截止频率增大到c2 ，系

自动控制原理课件：线性系统的校正

自动控制原理课件：线性系统的校正
1 s


U i (s) 1 ( R1 R2 )Cs 1 s
➢在整个频率范围内相位都
滞后，相位滞后校正。
滞后环节几乎不影响系统的高频相位；
但使系统的高频幅值衰减增大
19
01 滞后校正装置的频率特性：
20 lg Gc ( j )
1

m
j 1
Gc ( j )
线性系统的校正
CONTENTS
目
录
6.1
校正的基本概念
6.2
线性系统的基本控制规律
6.3
常用串联校正及特性
6.4
期望特性串联校正
6.5
MATLAB在线性控制系统校正
中的应用
6.1
校正的基本概念
为某种用途而设计的控制系统都必须满足一定的性能指标，如时域指标、
频域指标及广义的误差分析性能指标。
自动控制系统一般由控制器及被控对象组
m sin 1

1
1
1 sin m
1 sin m
11
03
小结
１．相位超前校正装置具有正的相角特性，利用这个特性，
可以使系统的相角裕量增大．
２．当 m 时，相角超前量最大．
３．最大超前角 m仅与 有关， 越小， m 越大．其关系可用
曲线表示．
13
02
3．选用相位超前校正装置．根据对相角裕量的要求，计算需
产生的最大相角超调量
0 40 15.52 5.52 30
4.
根据 m 确定 值
1 sin 30

0.333
1 sin 30
14

自动控制6第六章控制系统的综合与校正

自动控制6第六章控制系统的综合与校正

复合校正
同时采用串联校正和反馈校正的方法，对系 统进行综合校正，以获得更好的性能。
数字校正
利用数字技术对控制系统进行校正，具有灵 活性和高精度等优点。
02 控制系统性能指标及评价
控制系统性能指标概述
稳定性
准确性
系统受到扰动后，能否恢复到原来的 平衡状态或达到新的平衡状态的能力。
系统稳态误差的大小，反映了系统的 控制精度。
针对生产线上的各种工 艺要求，设计相应的控 制策略，如顺序控制、 过程控制等。
系统校正方法
根据生产效率和产品质 量要求，采用适当的校 正方法，如PID参数整定、 自适应控制等。
仿真与实验验证
通过仿真和实验手段， 验证综合与校正后的工 业自动化生产线控制系 统的稳定性和效率。
控制系统综合与校正的注
06 意事项与常见问题解决方 案
仿真与实验验证
通过仿真和实验手段，验证综合与校正后 的导弹制导控制系统的精确性和可靠性。
系统校正方法
针对导弹制导控制系统的性能要求，采用 适当的校正方法，如串联校正、反馈校正 等。
实例三
01
02
03
04
控制系统结构
分析工业自动化生产线 控制系统的组成结构， 包括传感器、执行机构、 PLC等部分。
控制策略设计
考虑多变量解耦控制
对于多变量控制系统，可以考虑采 用解耦控制策略，降低各变量之间 的相互影响，提高系统控制精度。
加强系统鲁棒性设计
考虑系统不确定性因素，加强 系统鲁棒性设计，提高系统对 各种干扰和变化的适应能力。
THANKS FOR WATCHING
感谢您的观看
控制系统综合与校正的注意事项
明确系统性能指标

自动控制原理_吴怀宇_第六章控制系统的校正与设计

自动控制原理_吴怀宇_第六章控制系统的校正与设计

扰动补偿 输入补偿
自动控制原理
按扰动补偿的复合控制系统如图6-3所示。
N(s)
+
Gn (s)
R(s) + E(s)
+
G1 (s)
G2 (s)
C(s)
-
图6-3 按扰动补偿的复合控制系统
自动控制原理
按给定补偿的复合控制系统如图6-4所示。
Gr ( s)
R( s) E( s)
+
G( s )
+
C( s)
自动控制原理
6.4.1 超前校正
基本原理：利用超前校正网络的相角超前特性去增大系 统的相角裕度，以改善系统的暂态响应。 用频率特性法设计串联超前校正装置的步骤：
（1）根据给定的系统稳态性能指标，确定系统的开环增益 ；
K）绘制在确定的 值下系统的伯德图，并计算其相角裕 （2 度 ； K 0
（3）根据给定的相角裕度 ，计算所需要的相角超前量 0
m
60º
40º
20º
1
0 4 8 12 14 20

图6-16 最大超前相角 m 与 的关系
自动控制原理
6.3.2 滞后校正装置 相位滞后校正装置可用图6-17所示的RC无源网络实现， 假设输入信号源的内阻为零，输出负载阻抗为无穷大，可 求得其传递函数为：
G c ( s) s zc s 1 1 s 1 ( ) s pc s 1 ( ) s 1
自动控制原理
与相位超前网络类似，相位滞后网络的最大滞后角位于
1 与 1 的几何中心处。
图6-21还表明相位滞后校正网络实际是一低通滤波器， 值 它对低频信号基本没有衰减作用，但能削弱高频噪声， 10 较为适宜。 愈大，抑制噪声的能力愈强。通常选择 一般可取

自动控制理论第版邹伯敏 共53页

自动控制理论第版邹伯敏 共53页
9
系统开环频率特性与系统性能指标密切相关，一般 可以将校正问题归纳为三类： 1、如果系统稳定且有较满意的暂态响应，但稳态
误差太大，这就必须增加低频段的增益来减小 稳态误差，同时保持中、高频特性不变； 2、如系统稳定且有较满意的误差，但其动态性能 较差，则应改变系统的中频段和高频段，以改 变系统的截止频率和相角裕度； 3、如果一个系统的稳态和动态性能均不能令人满 意，就必须增加低频增益，并改变中频段和高 频段。
自动控制理论
第六章
控制系统的校正
1
第一节 引 言
一、基本概念 1、系统校正
被控对象确定后，根据要求的控制目标，对
控制器的进行设计的过程叫作系统校正。
R

Gc
Y 对 象
2
2、控制目标——性能指标
时域调 超节 调时 量M间 pts% 性能指标 稳态误差 ess
频域谐 稳振 定峰 裕值 度 M，r,频 h，率幅带值宽 穿 b 越频率 c
40 30 20 10
m
m 增加不多。
m

tan1

2
1

0
10-2
10-1
ωm
100
101
14
三、超前校正环节的设计原理
频率法对系统进行校正的基本思路是：通过所 加校正装置，改变系统开环频率特性的形状，使校 正后系统的开环频率特性具有如下特点： 低频段：用以满足稳态精度的要求；
中频段：幅频特性的斜率为-20dB/dec,并具有较宽的 频带，这一要求是为了系统具有满意的动态性能；
0 10-2
10-1
ωm
1
G
c(s)
1 Ts 1 TsT s 1 1
s 2 1

自动控制系统课程设计---单位负反馈系统的校正设计

自动控制系统课程设计---单位负反馈系统的校正设计

自动控制系统课程设计---单位负反馈系统的校正设计
一、实验目的
本次实验的目的是利用单位负反馈设计实现系统输出相应的数值，以达到超调和补偿
的目的。

实验中参与的设备具体有：计算机、数据采集卡、DC机器电源、被测系统、LED
装置等。

二、实验原理
单位负反馈是控制系统中常用的方法，在实验中，单位负反馈会利用系统的输出信号
作为正反馈信号与理想信号做比较，当输出信号与理想信号不一致时，就会把误差反馈到
控制系统中，从而实现控制系统的超调和补偿。

三、实验方案
实验步骤
1、首先，将数据采集卡连接计算机，并使用VC语言编写实验程序，以设置系统的
控制级；
2、将DC机器电源连接被测系统，并利用数据采集卡采集被测系统的输出数据；
3、连接LED装置，它会根据控制系统的输出信号产生不同的颜色，从而实现系统的
颜色显示；
4、运行实验程序，观察被测系统的运行情况，检查输出的颜色，注意观察是否达到
理想超调和补偿的效果；
5、最后，记录实验结果并存档，进行实验的总结。

四、实验结果
实验运行后得到的颜色结果如下:
绿色：说明系统输出值处于可接受范围；
本次实验通过使用单位负反馈，使用数据采集卡以及VC语言编写实验程序来实现系
统的超调和补偿，并通过改变系统的控制参数来实现输出结果的调节。

通过本次实验，可
以使我们了解单位负反馈的工作原理，从而掌握使用单位负反馈在实际工程中的应用能力。

自动控制原理课程设计---单位负反馈系统设计校正

自动控制原理课程设计---单位负反馈系统设计校正

自动控制原理课程设计---单位负反馈系统设计校正
单位负反馈系统是自动控制原理课程设计中的重要内容，它是将输入信号与反馈信号进行比较、控制，从而达到调节系统性能的一种手段。

其目的是提高系统的稳定性和可靠性，缩小输入量的波动对输出量的影响，保持系统性能的稳定性和提高系统的控制性能，增强系统的鲁棒性。

系统的校正是保证其良好性能的前提，系统校正理论是所有反馈控制系统的基础之一，是实现系统自动控制的根本。

一、系统校正要点
1、调节器模式：调节器的类型是校正的核心，调节器的模式决定着反馈控制系统的性能。

常用的调节器有PI、PD、PID参数调节器，应根据实际情况灵活选择。

2、参数校正：选择调节器模式后，需要进行具体参数的校正，校正的过程一般有两种：经验法和数学模型法可以采用。

3、现场校正：现场校正过程主要是现场对参数进行实践调整，包括检查输入信号校正等，此类校正只能通过仪器进行，由于仪器的精度不同，校正效果也会有所不一样。

二、系统校正实施
1、系统检查：在校正实施前需要进行系统检查，检查项包括仪表精度以及反馈控制系统的结构与结构，检查后才能确定最佳的参数；
2、参数设置：在校正过程中，参数设置是提高反馈控制系统可用性的关键，特别是PID参数的调节，这要求改变参数时，要结合理论，灵活调整，以保证系统满足要求；
3、系统性能：在系统校正完成后，对系统性能进行检查，要求系统要满足设定的所有参数，结果必须与预期的结果保持一致，否则可以继续微调参数设置，以更好的满足需要。

总之，系统校正是自动控制原理中重要的一环，它既涉及到调整调节器参数，也涉及到系统调试等过程，必须根据实际情况，灵活选择，层层检查，从而实现反馈控制系统的良好性能。

控制系统的校正(PID).

控制系统的校正(PID).

E(s)
在前向通道上，相当于系统增加了一个位于原点的极点，和一 个s左半平面的零点，该零点可以抵消极点所产生的相位滞后， 以缓和积分环节带来的对稳定性不利的影响。
18
❖ 积分控制器的阶跃响应特性：
u(t)
比例积分作用
K ce
Ti
e(t)
比例作用
t
t
在单位阶跃偏差输入条
件下，每过一个积分时
间常数时间 T，积分项 i
静态误差系数K
p
,
K v
,K a
常常将时域指标转化为相应的频域指标进行校正装置的
设计
闭环频域指标
谐振峰值Mr ,谐振频率r
带宽频率b
开环频域指标
剪切频率c
幅值裕度Kg ,相角裕度
5
系统分析与校正的差别:
❖ 系统分析的任务是根据已知的系统，求出系统的性能指标 和分析这些性能指标与系统参数之间的关系，分析的结果 具有唯一性。
16
5.2.2 积分(I)控制
❖ 积分作用：
u(t ) 1
t
e( )d
Ti 0
传递函数为 U (s) 1 E(s) Tis
定义： T为i “积分时间常数”。
优缺点
前向通道上提高控制系统的型别，改善系统的稳态精度。
积分作用在控制中会造成过调现象，乃至引起被控参数 的振荡。因为u(t)的大小及方向，只决定于偏差e(t)的大 小及方向，而不考虑其变化速度的大小及方向。
❖ 将选定的控制对象和控制器组成控制系统，如果构成的系统不能 满足或不能全部满足设计要求的性能指标，还必须增加合适的元 件，按一定的方式连接到原系统中，使重新组合起来的系统全面 满足设计要求。
控制器
控制对象

自动控制系统的校正

自动控制系统的校正

自动控制系统的校正摘要:在工业上、农业、交通运输和国防各个方面，凡要求较高的场合，都离不开自动控制。

所谓自动控制，就是在没有人直接参与的情况下，利用控制装置，对生产过程、工艺参数、目标要求进行自动的调节与控制，使之按照预定的方案达到要求的指标。

自动控制系统性能的优劣，将直接影响到产品的产量、质量、成本、、劳动条件和预期目标的完成。

因此，自动控制越来越受人们的重视，使控制理论和技术应用方面因此也获得了飞速的发展。

关键词：自动控制校正1.自动控制系统的组成为了表明自动控制系统的组成以及信号的传递情况，通常把系统各个环节用框图表示，并用箭头标明各做用量的传递情况。

框图可以把系统的组成简单明了地表达出来，而不必画出具体线路自动控制的分类实际生产过程中采用的自动控制系统的类型是多种多样的，从不同的角度出发，可以进行不同的分类。

按输入量变化的规律分类有恒指控制系统、随动系统过程控制系统；按系统传输信号分类有连续控制系统、离散控制系统；按系统的输出量和输入量间的关系分类有线性系统、非线性系统；按系统中的参数对时间的变化情况分类有定常系统、时变系统。

对自动系统进行分析研究，首先是对系统进行定性分析。

所谓定性分析，主要是搞清各个单元及各个组件在系统中的地位和作用，以及它们之间的相互联系，并在此基础上搞清系统的工作原理。

然后，在定性分析的基础上，可以建立系统的数字模型；再应用自动控制理论对系统的稳定性、稳态性能和动态性能进行定量分析。

在系统分析的基础上就可以找到改善系统性能、提高系统技术指针的有效途径，这也就是系统的校正、设计和现场调试。

2.自动控制系统的校正当自动控制系统的稳态性能或动态性能满足所要求的性能指针时，首先可以考虑调整系统中的可以调整的参数；若通过调整参数仍是不能满足要求时，则可以在原有的系统中，有目的的添加一些装置和组件。

，认为的的改变系统的结构和性能，使之满足所要求的性能指针，我们把这种方法称为“系统校正”。

自动控制原理第四版习题答案

自动控制原理第四版习题答案
02
鲁棒控制系统的设计目标是使系统在不确定性和干扰作用下 仍能保持其稳定性和性能。
03
鲁棒控制理论中常用的方法有鲁棒性分析、鲁棒控制器设计 等。
06
习题答案解析
第1章习题答案解析
1.1
简述自动控制系统的基本组成。答案：一个典型的自动控制系统由控制器、受控对象、执行器、传感 器等部分组成。
1.2
简述开环控制系统和闭环控制系统的区别。答案：开环控制系统是指系统中没有反馈环节的系统，输 出只受输入的控制，结构相对简单；而闭环控制系统则有反馈环节，输出对输入有影响，结构相对复 杂。
20世纪60年代末至70年代，主要研究多变量线 性时不变系统的最优控制问题，如线性二次型最 优控制、极点配置等。
智能控制理论
20世纪80年代至今，主要研究具有人工智能的 控制系统，如模糊逻辑控制、神经网络控制等。
02
控制系统稳定性分析
稳定性定义
01
内部稳定性
系统在平衡状态下受到扰动后，能 够回到平衡状态的性能。
步骤
时域分析法包括对系统进行数学建模、 系统稳定性分析、系统性能分析和系 统误差分析等步骤。
缺点
时域分析法需要对系统的数学模型进 行详细的分析，对于复杂系统的分析 可能会比较困难。
频域分析法
步骤
频域分析法包括对系统进行数学建模、系 统稳定性分析和系统性能分析等步骤。
定义
频域分析法是在频率域中对控制系 统进行分析的方法。它通过对系统 的频率响应进行分析，来描述系统
它通过分析系统的频率响 应，并根据频率响应的性 质来判断系统的稳定性。
如果频率响应曲线超出奈 奎斯特圆，则系统是不稳 定的。
根轨迹法
根轨迹法是一种图解方法，用 于分析线性时不变系统的稳定

自动控制原理教案

自动控制原理教案

自动控制原理教案经典控制部分第一章控制理论一般概念3学时 (2)第二章控制系统的数学模型9学时 (6)第三章控制系统的时域分析10学时 (15)第五章频率特性12学时 (26)第六章控制系统的校正与设计8学时 (36)第七章非线性系统8学时 (40)第八章离散控制系统8学时 (45)第一章控制理论一般概念3学时1．本章的教学要求1）使学生了解控制工程研究的主要内容、控制理论的发展、控制理论在工程中的应用及控制理论的学习方法等内容，认识本学科在国民经济建设中的重要作用，从而明确学习本课程的目的。

2）使学生深入理解控制系统的基本工作原理、开环闭环和复合控制系统、闭环控制系统的基本组成等内容，学会利用所学控制原理分析控制系统。

3）使学生学会控制系统的基本分类方法，4）掌握对控制系统的基本要求。

2．本章讲授的重点本章讲授的重点是控制系统的基本概念、反馈控制原理、控制系统的的基本分类方法及对控制系统的基本要求。

3．本章的教学安排本课程讲授3个学时，复习学时3个。

演示《自动控制技术与人类进步》及《自动化的应用举例》幻灯片，加深同学对本课程研究对象和内容的了解，加深对反馈控制原理及系统参数对系统性能影响的理解。

[教案1-1]第一节概述1．教学主要内容：本讲主要介绍控制工程研究的主要内容、控制理论的发展、控制理论在工程中的应用及控制理论的学习方法等内容。

2．讲授方法及讲授重点：本讲首先介绍控制工程研究的主要内容，给出定义，并以瓦特发明的蒸汽机离心调速器为例，说明需要用控制理论解决控制系统的稳定、准确、快速等问题。

其次，在讲授控制理论的发展时，主要介绍控制理论的发展的三个主要阶段，重点说明经典控制理论、现代控制理论研究的范围、研究的手段，强调本课程重点介绍经典控制理论。

另外，在介绍控制理论在工程中的应用时，应举出控制理论在军事、数控机床、加工中心、机器人、机电一体化系统、动态测试、机械动力系统性能分析、液压系统的动态特性分析、生产过程控制等方面的应用及与后续课的关系，激发同学的学习兴趣。

自动控制理论第六章控制系统的校正与设计

自动控制理论第六章控制系统的校正与设计

第一节 系统校正的一般方法
幅相频率特性曲线：
Im
Gc(s)=
1+aTs 1+Ts
令
dφ(ω) dω
=0
得
ωm=
1 Ta
=
1 T
·aT1
0
φm 1ω=0 α+1
2
ω=∞
α Re
两个转折频率的几何中点。
最大超前相角：
sinφm=1+(a(a––11)/)2/2
=
a–1 a+1
φm=sin-1
a–1 a+1
滞后校正部分：
(1+ T1S) (1+αT1S)
超前校正部分：
(1+ T2S)
(1+
T2 α
S)
L(ω)/dB
1
1
0 α T1
T1
-20dB/dec
φ(ω)
0
1α
T2
T2
ω
+20dB/dec
ω
第一节 系统校正的一般方法
(2) 有源滞后—超前
R2
校正装置 传递函数为:
ur R1
GGcc(式(ss))中==K:(K1(cc1(+(1+1aK+T+TTcT01=S1S1S)SR)()()12(1R(+1+1+1+RT+TaT33T2S2S2S)S))) T1=
a=
1+sinφm 1–sinφm
第一节 系统校正的一般方法
(2) 有源超前校正装置
R2 C
R3
Gc(s)=
R3[1+(R1+R2)Cs] R1(1+R2Cs)

自动控制原理自动控制系统的校正

自动控制原理自动控制系统的校正

2021/8/5
3
举一个例子说明校正的作用。 上一章的例５-７：系统的开环传递函数为
G (s)H (s)
10
s(10.0s2 )1(0.2s)
首先分析一下，未校正系统的性能
稳态误差：有一个积分环节，是I型系统．
开环增益
，稳态速度误差系数
K10 而 Kp,Ka0
Kv10
2021/8/5
4
L()
40 20dB / dec
2021/8/5
1
概述
前面介绍了分析控制系统的三种基本方法： 时域分析法、根轨迹法和频域分析法。利用这些 方法能够在系统结构和参数已经确定的情况下， 计算或估算系统的性能指标：稳态性能指标和暂 态性能指标 。这类问题是系统的分析问题。
系统分析：已知结构、参数→数学模型→动、 静态性能分析→性能指标与参数的关系
1、稳态性能指标
系统的稳态性能与开环系统的型别v与开环传递系数K有关，常用静态误差系 数衡量，误差系数越大（等效于K越大），稳态误差ess就越小。
2021/8/5
8
2、动态性能指标
1）时域指标：最大超调量Mp（反映平稳性）、调节时间ts（反映快速性）。 2）频域指标：
（1）开环频域指标： 稳定性指标：相位裕量、幅值裕量GM、中频段宽度； 快速性指标：幅值穿越频率c。 （2）闭环频域指标：Mr、ωr、ωb 3）复域指标：
2021/8/5
10
二、校正的基本方式
1. 串联校正
R(s)
-
校正装置 Gc(s)
控制器
被控对象 C(s) Go(s)
校正装置和未校正系统的前向通道的环节相串联，这
种方式叫做串联校正。
优点：结构较简单，通常将串联校正装置安置在前向通

自动控制原理与系统__课件第五章自动控制系统的校正

自动控制原理与系统__课件第五章自动控制系统的校正

解：原系统的Bode图如图5-8中曲线I所示。特性曲线以-40dB/dec 的斜率穿越0dB线，穿越频率ωc=13.5dB，相位裕量γ=12.3o。 采用PD调节器校正，其传递函数Gc(s)=0.2s+1，Bode图为图58中的曲线II。
图5—7
11
图5—8
12
由图可见，增加比例微分校正装置后：
r
1 Gr (s)G1 (s)G 2 (s) E (s) R(s) C (s) 1 G1 (s)G 2 (s)
26
二、按扰动补偿的复合校正 如果满足 1+Gd(s)G1(s)=0 ，即 Gd(s)=-1/G1(s)时，则 系统因扰动而引起的误 差已全部被补偿（即 E(s)=0）。
综上所述，比例微分校正不影响系统的稳态精度, 将使系统的稳定性和快速性改善，但是抗高频干扰能 力下降。 串联比例微分校正一般用于系统稳态性能已满足 要求,但动态性能有待改善的系统。
13
2.比例积分校正（相位滞后校正）
C
C
图5-9
图5—9为一比例积分校正装置，也称为PI调节 器 K C (TC s 1) 传递函数 GC ( s )
第五章 控制系统的校正与设计
1
第一节 校正的基本概念
一、校正的概念
• 自动控制系统的主要任务就是实现对被 控对象的控制。
系统的执行元件、比较元件、放大元件和测量 元件等，除放大元件的放大系数可作适当调整 以外，其它元件的参数基本上是固定不变的， 称为系统的固有部分。 根据被控对象的工作条件、技术要求、工艺要 求、经济性要求以及可靠性要求等提出控制系 统的性能指标。
图5－15
不考虑输入控制，即R(s)=0时，扰动作用下的误差为
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一节 系统校正的一般方法
四、PID控制器
PI具D控有制PI是D控指制对系系统统结的构偏差信号e(t)
进行比例r(、t) 积e分(t) 、微分u(运t) 算后，c(t)通过线
性组合形成控_制量Guc(s()t)的一Go种(s)控制规律。
PID控制器 对象
比例系数 PID控制律的数学表达式: 微分时
3）而超动前态校性正能难有使待改原善系的统场的合低。频特性得到 改善。系统抗高频干扰的能力也变差。
第一节 系统校正的一般方法
二 、串联滞后校正
R1
+
+
1．滞后校正装置 (1) 无源超前校正装置
ur
-
R2
c
uc
-
Gc(s)=
1+βTs 1+Ts
T = (R1+R2)C
β= R1R+2R2< 1
同理：φωmm==sinT-β11 ββ+–11
a=
1+sinφm 1–sinφm
第一节 系统校正的一般方法
(2) 有源超前校正装置
R2 C
R3
Gc(s)=
R3[1+(R1+R2)Cs] R1(1+R2Cs)
ur
Δ
-∞
R1
+ +
uc
=Kc11++τTss
式中: 令:
Kc= aT=τ
R3 R1
τ=(R1+R2)C
Kc=1 则: a=
aT T
T=R2C
1 T
-ω
TG=c(RsR)1=1+为RaR12(了2+1Ca+补TTssa偿)=×开Ra1=环R+12R1放++2a大T>Tss1倍数α0φ>1(1ω/α) <1φω对(mφωm稳)>态0 精ω
度ω的>影ω响2 ，再=2增0l加g 一a 放大超倍前数的为相α的频放特大性环
L节(ω。)=20lgaωT-20lgωT ω=ωm处为最大超前角
=
R1+R2 R2
>1
Gc(s)=
1+aTs 1+Ts
第一节 系统校正的一般方法
2．超前校正装置的设计
超前校正是利用相位超前特性来增加系 统的相角稳定裕量，利用幅频特性曲线的正斜 率段增加系统的穿越频率。从而改善系统的平 稳性和快速性。为此，要求校正装置的最大超 前角出现在系统校正后的穿越频率处。
第一节 系统校正的一般方法
滞后校正有如下的特点：
1）滞后校正是利用其在中、高频段造成
的幅值衰减使系统的相位裕量增加，但同时 也会使系统的穿越频率减小。
2）一般的滞后校正不改变原系统最低
频段的特性，可用来改善系统的稳 态精度。
3）由于滞后校正使系统的高频幅值降 低，其抗高频干扰的能力得到加强。
第一节 系统校正的一般方法
穿6)越画频出率校正ω’后c 。系统的伯德图，并校核
相φ=位–裕18量0。o+γ'+Δ
Δ=5o~15o
第一节 系统校正的一般方法
例 系统结构如图,试设计滞后校正装置。
GφLG取要41对52Gc=003=0()=)=)().解)(ωsωωs求(ω5-应由-s确校)(s系1确-21ω)5=sK)c211=：==80'2+==于图定正c18统)Kβ=00定sβl8311G=g+0(.Kovo≈+)ωβ这5s可开装25T+o1≥0的(ω+1v+(=T0=γ5=Ts251个知s=4环’置ωd'.1伯=()c+5s5)B01Gγ4ω05(cγΔs=1角：o增0=参50d德'+.'c=ω+≥c10s(B-.≈11-5s+12：01益数4图2c')20)s2201=0(0+.so°s1)K1°0l+1+g05.1)11β0s--21+--R784229000000010(s0)LΦ).0((1Lωω()满φω)-/Ld0)Bc 足βγs(='=sL设+00401..φ101)计c(γ°K0ω.'要5s’c0+Φ.求511(ω)ω)2Cγc (s)ωω
L(ω ) dB
0
ω1=
1 T
ω2=
1
βT
20lgβ ω
φ (ω )
φm
0
ωm
ω
第一节 系统校正的一般方法
(2) 有源滞后校正装置
R2 C
Gc(s)=
R3(1+R2Cs) R1[1+(R2+R3)Cs]
=Kc11++τTss
ur R1 - ∞ R3 uc
+ +
式中:
Kc=
R3 R1
令: βT=τ Kc=1
第一节 系统校正的一般方法
例 设单位反馈系统的开环传递函数
G0 (s) =S(0.5S+K1)(S+1)
试设计一滞后-超前校正装置。
要求： Kv ≥ 10
γ ' ≥ 50°
解： 1）确定开环增益K
K = Kv = 10 2) 画出未校正系统的伯德图
第一节 系统校正的一般方法
GG则6451选3c取Gφ则c)l)/)选)2系L(T(开(择校T(确ωωγs(ω确α2ω确传0αω择)ω统ω=1=)环T=Tc传正)=1.定T)≈-1015定)==S定递=131α的==102.ω0ω=传=递后(=73超=..滞161ω111=ω函1c11–7c1o传1'+0.3.6++递+≈函系.50前6c5=31a51’后.6'0数1107递==66d08/..函1数统.部117T1.6BS04c部66.050函4.25°3数7.7的.+=分(361S分6SS数7S751.6)--217(--7998224000000G0000S.01ΦL0.+04(((1Lωω3s51()ω))S-)/2L)d(=0c1B+d(SωB.4)/(0φ1d.0φ30e1)(cc5ω.((SL5φωS)0S0)((+ωω+.7+))11γ111ω)0’1-))(.45’(00cω2Sd.B5c+-γ/6dS10e+dc7)B1/ωdω)ec
c1 R4 - ∞ c2
+ +
R2R3 R2+R3
C1
R3
uc
T0=R2C1 T2=(R2+R3)C2 T3=R4C2
令: Kc=1 T0>T1>T2>T3
T0 T1
=
T2 T3
=
R2+R3 R3
=
a>1
第一节 系统校正的一般方法
2．滞后-超前校正装置的设计
如果对校正后系统的动态和稳态性能均有 较高的要求，则采用滞后— 超前校正。利用校 正装置的超前部分来增大系统的相位裕量改善 动态性能；又利用校正装置的滞后部分来改善 系统的稳态性能。
一、串联超前校正 二、串联滞后校正 三、串联滞后—超前校正 四、PID控制器
第一节 系统校正的一般方法
一、串联超前校正
c
1．超前校正装置
对数频率特性曲线：
(1) 无源超前校正装置
+L(ω ) dBR1
+
Gc(s)=a1(+1+aTTss)
ur 10lgα
0
-
ω1=
1 aT
R2 20lugαc
ω2=
第一节 系统校正的一般方法
超前校正装置设计的一般步骤：
15））根找据到稳点态Lo指(ω标)=要-10求lg确α，定对开应环的增频益率K。为：
2）绘制原系统ω的m伯= 德ωc图' Lo(ω)和φ(ω) ， 36））大根并根超据确ω据2前要定=ωT相m求相1确=角的位ω定：γ裕m’校和α量正实γ装。际置的ω的γ1=，转α1确T折=定频ω最α率m 。 7）校φm验=γ系'–统γ+的Δ 相位裕Δ量=是5°~否2满0°足要求。 4）根如据果所不确满定足的要φ求m，,计则算重出新α选值择。△值。
第一节 系统校正的一般方法
幅相频率特性曲线：
Im
Gc(s)=
1+aTs 1+Ts
令
dφ(ω) dω
=0
得
ωm=
1 Ta
=
1 T
·aT1
0
φm 1ω=0 α+1
2
ω=∞
α Re
两个转折频率的几何中点。
最大超前相角：
sinφm=1+(a(a––11)/)2/2
=
a–1 a+1
φm=sin-1
a–1 a+1
第六章 控制系统的校正与设计
第六章 控制系统的校正与设计
校正：在系统中附加一些装置改变系统 的结构，从而改变系统的性能。
第一节 系统校正的一般方法 第二节 控制系统的工程设计方法 第三节 控制系统设计举例 第四节 MATLAB用于系统校正与设计
第六章 控制系统的校正与设计
第一节 系统校正的一般方法
三、串联滞后-超前校正
1．滞后-超前校正装置
(1)无源滞后-超前校正装置
c1
传递函数为：
+
Gc(s) =((11++αTT11SS))(1(+1+T2αTS2)S )
ur
-
+
R1 R2
c2
uc
-
其中： αT1 > T1 > T2 > T2 / α