控制系统的传递函数

《自动控制原理》MATLAB中的传递函数模型实验一、实验目的1、熟练运用matlab软件，求解控制系统数学模型2、掌握传递函数在matlab中的表达方法3、掌握matlab求解拉氏变换和反变换4、掌握matlab求系统极值点和零点判断系统稳定性二、实验仪器Matlab2014b版三、实验原理（一）MATLAB中的传递函数模型传递函数在matlab中的表达方法控制系统的传递函数模型为：在MATLAB中，分子/分母多项式通过其系数行向量表示，即：num = [b0 b1 … bm]den = [a0 a1 … an]此时，系统的传递函数模型用tf函数生成，句法为：sys=tf(num, den) 其中，sys为系统传递函数。

如：num = [1 5 0 2]; den = [2 3 15 8];则：sys=tf(num, den)输出为：Transfer function:若控制系统的模型形式为零极点增益形式：此时，系统的传递函数模型用zpk函数生成，句法为：sys=zpk(z, p, k)。

zpk函数也可用于将传递函数模型转换为零极点增益形式，句法为：zpksys=zpk(sys)如：z=[-0.5 -1 -3]; p=[1 -2 -1.5 -5]; k=10;sys=zpk(z, p, k)传递函数的转换[num,den]=zp2tf(z,p,k)[z,p,k]=tf2zp(num,den)实际系统往往由多个环节通过串联、并联及反馈方式互连构成。

MATLAB提供的三个用于计算串联、并联及反馈连接形成的新系统模型的函数。

series函数计算两子系统串联后的新系统模型。

句法：sys = series(sys1, sys2)sys1, sys2分别为两子系统模型parallel函数计算两子系统并联后的新系统模型。

句法： sys = parallel(sys1, sys2)feedback函数计算两子系统反馈互联后的新系统模型。

控制系统的传递函数定义
控制系统传递函数是描述控制系统输入与输出关系的数学模型，通常用于分析和设计控制系统。

它表示了输入信号经过控制系统后的输出信号，可以用数学公式表示为输出信号Y(s)与输入信号U(s)的关系：Y(s)=G(s)U(s)。

其中，G(s)为系统的传递函数，它是一个复数函数，描述了控制系统的动态特性和稳态特性。

传递函数的分母描述了系统的阻尼和自然频率，分子描述了系统的增益和相位，通过对传递函数进行分析可以得到系统的稳态误差、稳定性、响应速度等性能指标。

因此，传递函数是控制系统分析和设计的重要工具，对于掌握控制系统的动态特性和优化系统性能具有重要意义。

- 1 -。

自动控制原理传递函数自动控制原理中，传递函数是一个非常重要的概念。

传递函数可以描述控制系统的输入和输出之间的关系，通过传递函数，我们可以分析系统的动态特性，设计控制器，进行系统仿真和性能评估。

因此，了解和掌握传递函数的概念和应用是非常重要的。

首先，让我们来了解一下传递函数的定义。

传递函数是指控制系统的输出响应与输入信号之间的函数关系，通常用G(s)表示。

其中，s是复变量，表示系统的复频域变量。

传递函数可以是一个分式函数，也可以是一个多项式函数。

通过传递函数，我们可以方便地分析系统的频域特性和时域特性。

接下来，我们来看一下传递函数的应用。

在控制系统设计中，我们经常需要根据系统的要求设计控制器，使得系统的性能指标满足要求。

而传递函数可以帮助我们分析系统的稳定性、超调量、静态误差等性能指标，从而指导我们设计出合适的控制器。

此外，传递函数也可以用于系统的仿真和性能评估，通过对传递函数进行频域分析和时域分析，我们可以了解系统的动态特性，评估系统的性能，找出系统存在的问题并进行改进。

在实际工程中，我们经常会遇到各种各样的控制系统，比如电机控制系统、飞行器控制系统、机器人控制系统等。

而这些控制系统的动态特性往往是非常复杂的，需要通过传递函数进行分析和设计。

因此，掌握传递函数的应用是非常重要的。

最后，让我们来总结一下传递函数的重要性。

传递函数是描述控制系统输入和输出之间关系的重要工具，通过传递函数，我们可以分析系统的动态特性，设计控制器，进行系统仿真和性能评估。

在实际工程中，掌握传递函数的应用是非常重要的，可以帮助我们设计出性能优良的控制系统。

综上所述，传递函数在自动控制原理中具有非常重要的地位和作用。

通过对传递函数的理解和应用，我们可以更好地理解和设计控制系统，提高系统的性能和稳定性。

希望本文能够帮助读者更好地理解传递函数的概念和应用，提高对自动控制原理的理解和应用能力。

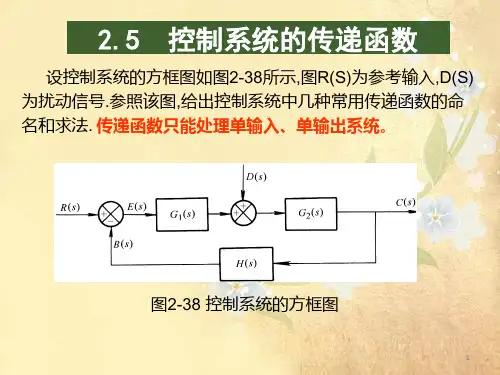
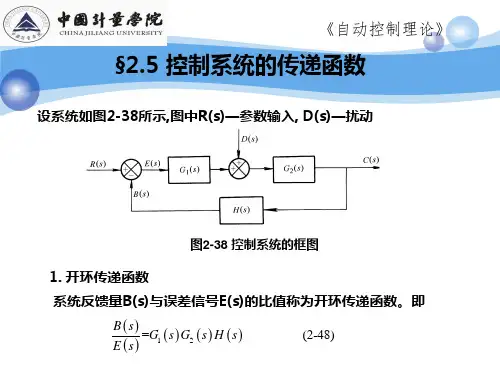
控制系统的传递函数考虑扰动的闭环控制系统X i (s )到X o (s )的信号传递通路称为前向通道；X o (s )到B (s )的信号传递通路称为反馈通道；1.闭环系统的开环传递函数将闭环控制系统主反馈通道的输出断开，即H (s )的输出通道断开，此时，前向通道传递函数与反馈通道传递函数的乘积G 1(s )G 2(s )H (s )称为该 闭环控制系统的开环传递函数。

记为G K (s )。

闭环系统的开环传递函数也可定义为反馈信号B (s )和偏差信号ε (s )之间的传递函数，即：2..x i (t )作用下系统的闭环传递函数令n (t )=0，此时在输入x i (t )作用下系统的闭环传递函数为：输入作用下系统的偏差传递函数 令n (t )=0，此时系统输入X i (s )与偏差ε (s )之间的传递函数称为输入作用下的偏差传递函数。

用)(s i εΦ表示。

3.n (t )作用下系统的闭环传递函数令x i (t )=0，此时在扰动n (t )作用下系统的闭环传递函数（干扰传递函数）为：扰动作用下系统的偏差传递函数，令x i (t )=0，此时系统在扰动作用下的偏差传递函数（称扰动偏差传递函数）。

)()()(1)()()()()(212101s H s G s G s G s G s X s X s i i +==Φ)()()(11)()()(21s H s G s G s X s s i i i +==Φεε)()()(1)()()()(21202s H s G s G s G s N s X s N +==Φ)()()(1)()()()()(212s H s G s G s H s G s N s s N N +-==Φεε。

控制系统传递函数优化控制系统传递函数优化是控制工程领域一个重要的问题，它涉及到提高控制系统的性能和稳定性，以及减少系统的成本和复杂性。

通过对传递函数进行优化，可以改善系统的响应速度、稳定性和鲁棒性，从而更好地满足实际控制需求。

本文将介绍控制系统传递函数优化的一些主要方法和思路。

一、传递函数的概念与作用在控制系统中，传递函数是描述输入和输出之间关系的数学模型。

它可以将输入信号转换为输出信号，并代表了系统对输入信号的响应。

传递函数是控制系统设计和优化的重要基础，通过对传递函数进行分析和调整，可以改变系统的特性，以满足实际的控制要求。

二、控制系统传递函数的优化方法1. 参数调整法控制系统的参数对系统的性能和稳定性有重要影响。

通过调整传递函数中的参数，可以改变系统的动态特性和频率响应，从而实现对系统性能的优化。

常用的参数调整方法包括试错法、频域法和优化算法等。

2. 标定法标定是通过实验测量和数据处理，确定系统传递函数中的参数值。

通过对系统进行标定，可以获取准确的传递函数模型，从而更好地进行优化设计。

标定方法包括试验法、辨识法、信号分析法等。

3. 系统结构优化法控制系统的结构对系统的性能和复杂度有重要影响。

通过调整传递函数的结构，可以优化系统的性能和复杂度。

常用的系统结构优化方法包括模型简化、参数化控制等。

4. 级联与并联级联与并联是对控制系统传递函数的一种特殊组合方式。

通过将多个传递函数进行级联或并联，可以改变系统的动态特性和频率响应，从而实现对系统性能的优化。

级联和并联方法可以用于系统的增益补偿、频率响应调整等。

5. 频率域设计法频率域设计法是一种基于频域特性的传递函数优化方法。

通过分析系统在不同频率下的响应特性，可以对传递函数进行频率响应设计，以满足实际需求。

常用的频率域设计法包括根轨迹法、频率响应法等。

三、案例分析以某工业过程的温度控制系统为例，通过对传递函数进行优化，实现对系统的性能提升和稳定性改善。