第四章控制系统的传递函数
- 格式:ppt
- 大小:1.17 MB
- 文档页数:38
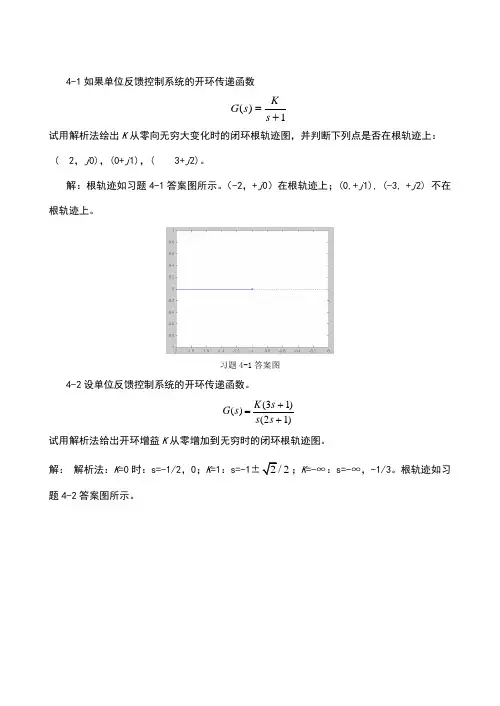
4-1如果单位反馈控制系统的开环传递函数1)(+=s K s G 试用解析法绘出K 从零向无穷大变化时的闭环根轨迹图,并判断下列点是否在根轨迹上: (2,j 0),(0+j 1),(3+j 2)。
解:根轨迹如习题4-1答案图所示。
(-2,+j 0)在根轨迹上;(0,+j 1), (-3, +j 2) 不在根轨迹上。
习题4-1答案图4-2设单位反馈控制系统的开环传递函数。
)12()13()(++=s s s K s G试用解析法给出开环增益K 从零增加到无穷时的闭环根轨迹图。
解: 解析法:K =0时:s=-1/2,0;K =1:s=-122;K =-∞:s=-∞,-1/3。
根轨迹如习题4-2答案图所示。
习题4-2答案图4-3 已知系统的开环传递函数)1()1()()(-+=s s s K s H s G ,试按根轨迹规则画出该系统的根轨迹图,并确定使系统处于稳定时的K 值范围。
解:分离点:;会合点: ;与虚轴交点:±j 。
稳定的K 值范围:K >1。
根轨迹如习题4-3答案图所示。
习题4-3答案图4-4已知一单位反馈系统的开环传递函数为2*)4)(1)(1()(+-+=s s s K s G (1)试粗略画出K *由0到∞的根轨迹图;(2)分析该系统的稳定性。
解:稳定性分析:系统不稳定。
根轨迹如习题4-4答案图所示。
-10-505-8-6-4-22468Root LocusReal AxisI m a g i n a r y A x i s习题4-4答案图4-5 设控制系统的开环传递函数为)164)(1()1()()(2*++-+=s s s s s K s H s G ,试绘制系统根轨迹图,并确定使系统稳定的开环增益范围。
解:渐近线:=60°,180°;=-2/3;复数极点出射角55°;分离会合点和;与虚轴交点和;使系统稳定的开环增益为 <K < (即 <K *<。



控制系统的传递函数定义
控制系统传递函数是描述控制系统输入与输出关系的数学模型,通常用于分析和设计控制系统。
它表示了输入信号经过控制系统后的输出信号,可以用数学公式表示为输出信号Y(s)与输入信号U(s)的关系:Y(s)=G(s)U(s)。
其中,G(s)为系统的传递函数,它是一个复数函数,描述了控制系统的动态特性和稳态特性。
传递函数的分母描述了系统的阻尼和自然频率,分子描述了系统的增益和相位,通过对传递函数进行分析可以得到系统的稳态误差、稳定性、响应速度等性能指标。
因此,传递函数是控制系统分析和设计的重要工具,对于掌握控制系统的动态特性和优化系统性能具有重要意义。
- 1 -。


目录第一章自动控制系统的基本原理第一节控制系统的工作原理和基本要求第二节控制系统的基本类型第三节典型控制信号第四节控制理论的内容和方法第二章控制系统的数学模型第一节机械系统的数学模型第二节液压系统的数学模型第三节电气系统的数学模型第四节线性控制系统的卷积关系式第三章拉氏变换第一节傅氏变换第二节拉普拉斯变换第三节拉普拉斯变换的基本定理第四节拉普拉斯逆变换第四章传递函数第一节传递函数的概念与性质第二节线性控制系统的典型环节第三节系统框图及其运算第四节多变量系统的传递函数第五章时间响应分析第一节概述第二节单位脉冲输入的时间响应第三节单位阶跃输入的时间响应第四节高阶系统时间响应第六章频率响应分析第一节谐和输入系统的定态响应第二节频率特性极坐标图第三节频率特性的对数坐标图第四节由频率特性的实验曲线求系统传递函数第七章控制系统的稳定性第一节稳定性概念第二节劳斯判据第三节乃奎斯特判据第四节对数坐标图的稳定性判据第八章控制系统的偏差第一节控制系统的偏差概念第二节输入引起的定态偏差第三节输入引起的动态偏差第九章控制系统的设计和校正第一节综述第二节希望对数幅频特性曲线的绘制第三节校正方法与校正环节第四节控制系统的增益调整第五节控制系统的串联校正第六节控制系统的局部反馈校正第七节控制系统的顺馈校正第一章自动控制系统的基本原理定义:在没有人的直接参与下,利用控制器使控制对象的某一物理量准确地按照预期的规律运行。
第一节控制系统的工作原理和基本要求一、控制系统举例与结构方框图例1.一个人工控制的恒温箱,希望的炉水温度为100C°,利用表示函数功能的方块、信号线,画出结构方块图。
图1人通过眼睛观察温度计来获得炉内实际温度,通过大脑分析、比较,利用手和锹上煤炭助燃。
比较图2例2.图示为液面高度控制系统原理图。
试画出控制系统方块图和相应的人工操纵的液面控制系统方块图。
解:浮子作为液面高度的反馈物,自动控制器通过比较实际的液面高度与希望的液面高度,调解气动阀门的开合度,对误差进行修正,可保持液面高度稳定。

《控制工程基础》第四章习题解题过程和参考答案4-1 设单位反馈系统的开环传递函数为:10()1G s s =+。
当系统作用有下列输入信号时:()sin(30)r t t =+︒,试求系统的稳态输出。
解:系统的闭环传递函数为:10()()11()()1()111C s G s s s R s G s Φ===++这是一个一阶系统。
系统增益为:1011K =,时间常数为:111T =其幅频特性为:()A ω=其相频特性为:()arctan T ϕωω=- 当输入为()sin(30)r t t =+︒,即信号幅值为:1A =,信号频率为:1ω=,初始相角为:030ϕ=︒。
代入幅频特性和相频特性,有:1(1)A ====11(1)arctan arctan5.1911T ωϕω==-=-=-︒所以,系统的稳态输出为:[]()(1)sin 30(1)24.81)c t A A t t ϕ=⋅⋅+︒+=+︒4-2 已知系统的单位阶跃响应为:49()1 1.80.8(0)ttc t e e t --=-+≥。
试求系统的幅频特性和相频特性。
解:对输出表达式两边拉氏变换:1 1.80.8361()49(4)(9)(1)(1)49C s s s s s s s s s s =-+==++++++由于()()()C s s R s =Φ,且有1()R s s =(单位阶跃)。
所以系统的闭环传递函数为:1()(1)(1)49s s sΦ=++ 可知,这是由两个一阶环节构成的系统,时间常数分别为:1211,49T T == 系统的幅频特性为二个一阶环节幅频特性之积,相频特性为二个一阶环节相频特性之和:12()()()A A A ωωω===1212()()()arctan arctan arctanarctan49T T ωωϕωϕωϕωωω=+=--=--4-3 已知系统开环传递函数如下,试概略绘出奈氏图。
(1)1()10.01G s s =+ (2)1()(10.1)G s s s =+(3))1008()1(1000)(2+++=s s s s s G (4)250(0.61)()(41)s G s s s +=+ 解:手工绘制奈氏图,只能做到概略绘制,很难做到精确。

自动控制原理第四章答案在自动控制原理的学习中,第四章是一个重要的环节,本章主要讲解了控制系统的稳定性。
在这一章节中,我们将学习如何分析控制系统的稳定性,并且掌握相应的解决方法。
接下来,我将为大家详细介绍第四章的内容及答案。
1. 什么是控制系统的稳定性?控制系统的稳定性是指当系统受到干扰时,系统能够保持平衡状态或者在一定的范围内回到平衡状态的能力。
在控制系统中,稳定性是一个非常重要的指标,它直接关系到系统的可靠性和性能。
2. 如何分析控制系统的稳定性?要分析控制系统的稳定性,我们通常采用的方法是利用系统的传递函数进行分析。
通过传递函数的极点和零点,我们可以判断系统的稳定性。
另外,我们还可以利用根轨迹法、Nyquist法、Bode图等方法进行分析。
3. 控制系统的稳定性解决方法有哪些?针对不同的稳定性问题,我们可以采取不同的解决方法。
比如,对于系统的根轨迹出现在右半平面的情况,我们可以采取根轨迹设计法进行修正;对于系统的相位裕度不足的情况,我们可以采取相位裕度补偿的方法进行调整。
4. 控制系统的稳定性分析在工程中的应用。
控制系统的稳定性分析在工程中有着广泛的应用,比如在飞行器、汽车、机器人等自动控制系统中,稳定性分析是至关重要的。
只有保证了系统的稳定性,才能确保系统的可靠性和安全性。
5. 总结。
通过本章的学习,我们对控制系统的稳定性有了更深入的了解。
掌握了稳定性分析的方法和解决方案,我们可以更好地应用于工程实践中,提高系统的性能和可靠性。
希望本文的内容能够帮助大家更好地理解自动控制原理第四章的内容,并且在学习和工程实践中取得更好的成绩。
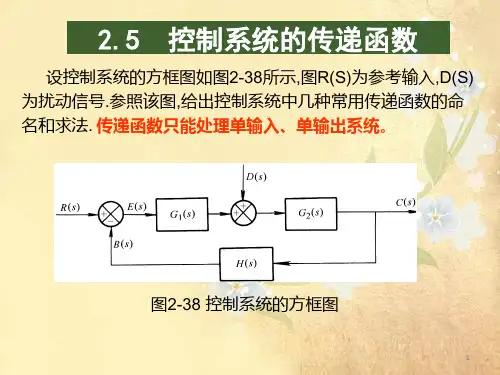
第二章 线性系统的状态空间分析法§1 线性系统的状态空间描述 §2 线性定常连续系统的分析 §3 线性定常离散系统的分析 §4 系统的传递函数矩阵一、定义及表达式零初始条件下,输出向量的拉氏变换式与输入向量 的拉氏变换式之间的传递关系——传递函数矩阵。
& ⎧ x(t ) = Ax(t ) + Bu(t ) ⇒ sX(s ) = AX(s ) + BU (s ) ⎨ ⎩y (t ) = Cx(t ) + Du(t ) ⇒ Y(s ) = CX(s ) + DU(s )∴ X(s ) = (sI − A ) BU (s )−1∴ Y(s ) = C(sI − A ) BU (s ) + DU(s ) = G (s )U(s )−1G (s ) = C(sI − A ) B + D−1q× p1⎡Y1 (s )⎤ ⎡G11 (s ) G12 (s ) L G1 p (s )⎤ ⎡U1 (s ) ⎤ ⎢Y (s )⎥ ⎢G (s ) G (s ) L G (s )⎥ ⎢U (s )⎥ 22 2p ⎢ 2 ⎥ = ⎢ 21 ⎥⎢ 2 ⎥ ⎢ M ⎥ ⎢ M M M ⎥⎢ M ⎥ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢Yq (s )⎥ ⎢Gq1 (s ) Gq 2 (s ) L Gqp (s )⎥ ⎢U p (s )⎥ ⎣ ⎦ ⎣ ⎦⎣ ⎦Y1 (s ) = G11 (s )U1 (s ) + G12 (s )U 2 (s ) + L + G1 j (s )U j (s ) + L + G1 p (s )U p (s )Yi (s ) = Gi1 (s )U1 (s ) + Gi 2 (s )U 2 (s ) + L + Gij (s )U j (s ) + L + Gip (s )U p (s )Yq (s ) = Gq1 (s )U1 (s ) + Gq 2 (s )U 2 (s ) + L + Gqj (s )U j (s ) + L + Gqp (s )U p (s )Gij (s ) =Yi (s ) , i = 1,2, L , q; j = 1,2 ,L ,p U j (s )第 j 个输入与第i 个输出之间的传递函数。