(完整版)点的运动学
- 格式:ppt
- 大小:1.49 MB
- 文档页数:1





第二部分 运动学第六章点的运动学一、基本要求1.掌握描述点的运动的矢量法、直角坐标法和自然法(弧坐标法)。
2.了解描述点的运动的极坐标法。
3.能求点的运动轨迹。
4.能熟练地应用直角坐标法和自然法求解与点的速度和加速度有关的问题。
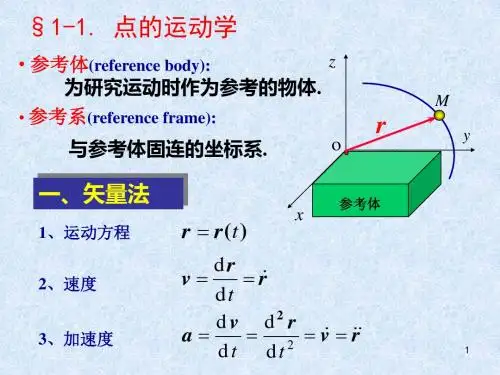
二、理论要点1.描述点的运动的三种基本方法(1)矢量法z 运动方程点的运动方程为动点在空间的几何位置随时间变化的规律。
以矢量形式表示的点的运动方程为)(t r r =z 轨迹轨迹为动点在空间运动时所经过的一条连续曲线。
在矢量法中,矢径r 的矢端曲线即为点的运动轨迹。
z 速度点的速度是个矢量,它等于矢径对时间的一阶导数,即dtd r v = z 加速度点的加速度也是个矢量,它等于速度矢对时间的一阶导数,或等于矢径对时间的二阶导数,即2dtd dt d 2r v a == (2)直角坐标法z 运动方程)()()(321t f z t f y t f x ===z 轨迹从上面点的运动方程中消去时间t 即可得轨迹方程。
如:),(0),(21==z y F y x Fz 速度 k j i v z y x v v v ++=dtdz v dt dy v dtdx v z y x ===即速度在各坐标轴上的投影等于动点的各对应坐标对时间的一阶导数。
由此可求得速度的大小和方向余弦。
z 加速度k j i a z y x a a a ++=222222dtz d dt dv a dty d dt dv a dtx d dt dv a z z y y x x ====== 即加速度在各坐标轴上的投影等于动点的各对应坐标对时间的二阶导数。
由此可求得加速度的大小和方向余弦。
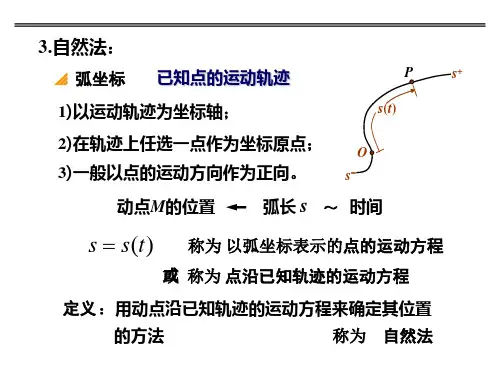
(3)自然法(弧坐标法)利用点的运动轨迹建立弧坐标及自然轴系,并用它们来描述和分析点的运动的方法称为自然法。
z 运动方程)(t f s =z 速度ττv dtds v == z 加速度 n τa a a n τn τa a +=+=22dt s d dt dv a τ== ρ2v a n =式中,ρ为曲率半径。



