(导学)6点的运动学

第六章 点的运动学6-1 从水面上方高20m 的岸上一点A ，用长为40m 的绳系住一船B 。

今在A 处以3m/s υ=的均速拉绳，使船靠岸，求5s 末船的速度是多少？在5s 内船移动了多少距离。

解：1）建立坐标系Ox 如图，则动点B的位置坐标为(t)B x =0t =时，(0)34.64m B x ==5s t =时，(5)15m B x ==5s 内船移动的距离(5)(0)34.641519.64m B B s x x ∆=-=-=2）船的速度(t)(t)(40B B x υ==5s t =时，75(5)5m /s 15B υ-===-（沿x 轴反方向） 6-2 已知点的运动方程为250,5005x t y t ==-（y 单位为m 、t 单位为s ）。

求当t=0时，点的切向加速度、法向加速度及轨迹的曲率半径。

解：1）由点的运动矢量法知： 运动方程为250(5005)r ti t j =+-；速度5010v r i tj ==-，速度大小v ==加速度10a v j ==-，加速度大小210/a m s ==；t=0时，050/v m s = 2）由点的运动自然法知： 切向加速度dva dtττ==；法向加速度2n v a n ρ==； t=0时，(0)0a τ=，2(0)10/n a a m s ==，220050250(0)10n v m a ρ===6-3 图示摇杆滑道机构中的滑块M 同时在固定的圆弧槽BC 和摇杆OA 的滑道中滑动。

如弧BC 的半径为R ，摇杆OA 的轴O 在弧BC 的圆周上。

摇杆绕O 轴以等角速度ω转动，当运动开始时，摇杆在水平位置。

试分别用直角坐标法和自然法给出点M 的运动方程，并求其速度和加速度。

解：直角坐标法：1） 建立直角坐标系1o xy 如图，则动点M 的 2） 运动方程cos 2sin 2r R ti R tj ωω=+3） 速度2sin 22cos 2v r R ti R tj ωωωω==-+；速度大小2v R ω==4） 加速度224cos 24sin 2a v R ti R tjωωωω==-- 加速度大小24a R ω== 自然法：1） 建立弧坐标系如图，M o 为原点，ω方向为正方向，则 2） 动点M 的运动方程2s R t ω= 3） 速度2v s R τωτ==4）加速度2204n n v a a a a n R n τωρ=+=+==第七章 刚体的基本运动7-1 图示为把工件送入干燥炉内的机构，叉杆OA=1.5m 在铅垂面内转动，杆AB=0.8m ，A 端为铰链，B 端有放置工件的框架。

第一篇静力学第1 章静力学公理与物体的受力分析1.1 静力学公理公理1 二力平衡公理：作用于刚体上的两个力，使刚体保持平衡的必要和充分条件是：这两个力大小相等、方向相反且作用于同一直线上。

F=-F’工程上常遇到只受两个力作用而平衡的构件，称为二力构件或二力杆。

公理2 加减平衡力系公理：在作用于刚体的任意力系上添加或取去任意平衡力系，不改变原力系对刚体的效应。

推论力的可传递性原理：作用于刚体上某点的力，可沿其作用线移至刚体内任意一点，而不改变该力对刚体的作用。

公理3 力的平行四边形法则：作用于物体上某点的两个力的合力，也作用于同一点上，其大小和方向可由这两个力所组成的平行四边形的对角线来表示。

推论三力平衡汇交定理：作用于刚体上三个相互平衡的力，若其中两个力的作用线汇交于一点，则此三个力必在同一平面内，且第三个力的作用线通过汇交点。

公理4 作用与反作用定律：两物体间相互作用的力总是同时存在，且其大小相等、方向相反，沿着同一直线，分别作用在两个物体上。

公理5 钢化原理：变形体在某一力系作用下平衡，若将它钢化成刚体，其平衡状态保持不变。

对处于平衡状态的变形体，总可以把它视为刚体来研究。

1.2 约束及其约束力１．柔性体约束２．光滑接触面约束３．光滑铰链约束第2章平面汇交力系与平面力偶系1.平面汇交力系合成的结果是一个合力,合力的作用线通过各力作用线的汇交点,其大小和方向可由失多边形的封闭边来表示,即等于个力失的矢量和,即F R=F1+F2+…..+Fn=∑F2.矢量投影定理：合矢量在某轴上的投影，等于其分矢量在同一轴上的投影的代数和。

3.力对刚体的作用效应分为移动和转动。

力对刚体的移动效应用力失来度量；力对刚体的转动效应用力矩来度量，即力矩是度量力使刚体绕某点或某轴转动的强弱程度的物理量。

（Mo（F）=±Fh）4.把作用在同一物体上大小相等、方向相反、作用线不重合的两个平行力所组成的力系称为力偶，记为（F,F’）。

第一章静力学公理和物体的受力分析一、是非判断题1.1 在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ) 1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( ) 1.3 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( ) 1.4 力的可传性只适用于刚体，不适用于变形体。

( ) 1.5两点受力的构件都是二力杆。

( )1.6只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( ) 1.7力的平行四边形法则只适用于刚体。

( ) 1.8 凡矢量都可以应用平行四边形法则合成。

( ) 1.9只要物体平衡，都能应用加减平衡力系公理。

( ) 1.10 凡是平衡力系，它的作用效果都等于零。

( ) 1.11合力总是比分力大。

( ) 1.12只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( ) 1.13若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ) 1.14当软绳受两个等值反向的压力时，可以平衡。

( ) 1.15静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ) 1.16静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

) 1.17 凡是两端用铰链连接的直杆都是二力杆。

（）1.18 如图所示三铰拱，受力F ，F1作用，其中F作用于铰C的销子上，则AC、BC构件都不是二力构件。

（）二、填空题1.1力对物体的作用效应一般分为效应和效应。

1.2 对非自由体的运动所预加的限制条件称为；约束力的方向总是与约束所能阻止的物体的运动趋势的方向；约束力由力引起，且随力的改变而改变。

1.3图示三铰拱架中，若将作用于构件AC上的力偶M处的约束力。

A. 都不变；B. 只有C处的不改变；C. 都改变；D. 只有C处的改变。

第二章一、是非判断题1.1当刚体受三个不平行的力作用时，只要这三个力的作用线汇交于同一点，则刚体一定处于平衡状态。

理论力学知识点总结理论力学是一门研究物体机械运动一般规律的学科，它是许多工程技术领域的基础。

以下是对理论力学一些重要知识点的总结。

一、静力学静力学主要研究物体在力系作用下的平衡问题。

1、力的基本概念力是物体之间的相互作用，具有大小、方向和作用点三个要素。

力的表示方法包括矢量表示和解析表示。

2、约束与约束力约束是限制物体运动的条件，约束力则是约束对物体的作用力。

常见的约束类型有柔索约束、光滑接触面约束、光滑圆柱铰链约束等，每种约束对应的约束力具有特定的方向和特点。

3、受力分析对物体进行受力分析是解决静力学问题的关键步骤。

要明确研究对象，画出其隔离体，逐个分析作用在物体上的力，包括主动力和约束力，并画出受力图。

4、力系的简化力系可以通过平移和合成等方法进行简化，得到一个合力或合力偶。

力的平移定理指出，力可以平移到另一点，但必须附加一个力偶。

5、平面力系的平衡方程平面任意力系的平衡方程有三个：∑Fx ＝ 0，∑Fy ＝ 0，∑Mo(F) ＝0。

对于平面汇交力系和平面力偶系，平衡方程分别有所简化。

6、空间力系的平衡方程空间力系的平衡方程数量增多，需要考虑三个方向的力平衡和三个方向的力矩平衡。

二、运动学运动学研究物体的运动而不考虑引起运动的力。

1、点的运动学描述点的运动可以使用矢量法、直角坐标法和自然法。

在自然法中，引入了弧坐标、切向加速度和法向加速度的概念。

2、刚体的基本运动刚体的基本运动包括平动和定轴转动。

平动时，刚体上各点的运动轨迹相同、速度和加速度相同；定轴转动时，刚体上各点的角速度和角加速度相同。

3、点的合成运动点的合成运动是指一个动点相对于两个不同参考系的运动。

通过选取合适的动点、动系和定系，运用速度合成定理和加速度合成定理来求解问题。

4、刚体的平面运动刚体平面运动可以分解为随基点的平动和绕基点的转动。

平面运动刚体上各点的速度可以用基点法、速度投影定理和瞬心法求解，加速度则可以用基点法求解。

三、动力学动力学研究物体的运动与作用力之间的关系。

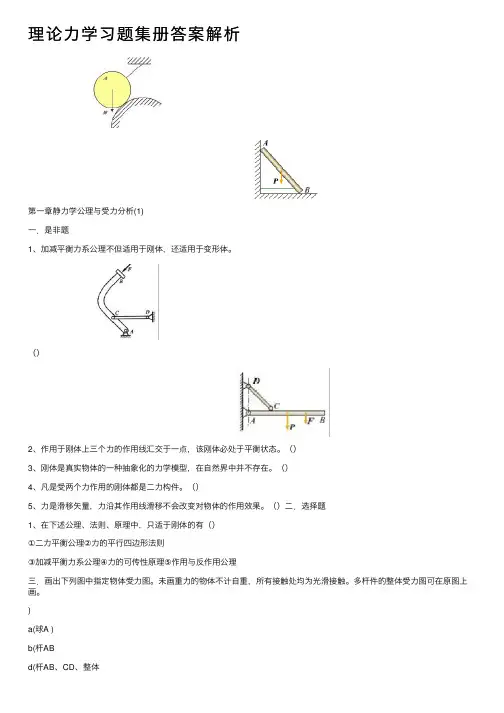
理论⼒学习题集册答案解析第⼀章静⼒学公理与受⼒分析(1)⼀．是⾮题1、加减平衡⼒系公理不但适⽤于刚体，还适⽤于变形体。

（）2、作⽤于刚体上三个⼒的作⽤线汇交于⼀点，该刚体必处于平衡状态。

（）3、刚体是真实物体的⼀种抽象化的⼒学模型，在⾃然界中并不存在。

（）4、凡是受两个⼒作⽤的刚体都是⼆⼒构件。

（）5、⼒是滑移⽮量，⼒沿其作⽤线滑移不会改变对物体的作⽤效果。

（）⼆．选择题1、在下述公理、法则、原理中，只适于刚体的有（）①⼆⼒平衡公理②⼒的平⾏四边形法则③加减平衡⼒系公理④⼒的可传性原理⑤作⽤与反作⽤公理三．画出下列图中指定物体受⼒图。

未画重⼒的物体不计⾃重，所有接触处均为光滑接触。

多杆件的整体受⼒图可在原图上画。

)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四．画出下列图中指定物体受⼒图。

未画重⼒的物体不计⾃重，所有接触处均为光滑接触。

多杆件的整体受⼒图可在原图上画。

)a(球A、球B、整体)b(杆BC、杆AC、整体- 2 -第⼀章静⼒学公理与受⼒分析（2）⼀．画出下列图中指定物体受⼒图。

未画重⼒的物体不计⾃重，所有接触处均为光滑接触。

多杆件的整体受⼒图可在原图上画。

WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体 )b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体- 4 -第⼆章平⾯汇交和⼒偶系⼀．是⾮题1、因为构成⼒偶的两个⼒满⾜F= - F’，所以⼒偶的合⼒等于零。

（）2、⽤解析法求平⾯汇交⼒系的合⼒时，若选⽤不同的直⾓坐标系，则所求得的合⼒不同。

第二篇运动学·第六章点的运动学·6.1 矢量法2. 6-6．下列说法正确的是。

（A）点的位移就是点走过的路程（B）点的矢端曲线，就是点运动的轨迹（C）如果在运动中点的矢径保持不变，点必作直线运动（D）如果在运动中点的矢径没有增量，点的速度一定为零参考答案：BD3. 6-7．下列说法正确的是。

（A）位移是矢量（B）当点作直线运动时，位移不是矢量（C）当点作曲线运动时，位移也可以是代数量（D）不论运动轨迹如何，位移一定是矢量参考答案：AD4. 6-1．运动学是研究物体运动的几何性质的科学。

（）.参考答案：√5. 6-2．运动学中通常采用两种参考系：定参考系和动参考系。

（）.参考答案：√6. 6-3．运动方程反映了物体运动的速度与时间的对应规律。

（）.参考答案：×7. 6-4．点的加速度等于矢径对时间的一阶导数。

（）.参考答案：×第二篇运动学·第六章点的运动学·6.2 直角坐标法3. 6-13．下列说法正确的是。

（A）在直角坐标法中，点的坐标和时间的对应关系，就是点的运动方程（B）当点作直线运动时，位移就等于路程（C）点作匀变速直线运动时，点的加速度和速度方向一定相同（D）点作匀速直线运动时，加速度一定为零参考答案：AD4. 6-8．动点的速度在直角坐标轴上的投影等于该点的对应坐标对时间的一阶导数。

（）.参考答案：√5. 6-9．动点的加速度在直角坐标轴上的投影等于该点速度的对应投影对时间的一阶导数。

（）.参考答案：√6. 6-10．点作直线运动时，若有加速度存在，则加速度必沿着直线方向。

（）.参考答案：√第二篇运动学·第六章点的运动学·6.3 自然法2. 6-20．点M 沿螺线自外向内运动，它走过的弧长与时间的一次方成正比，则该点（）。

（A）越跑越快（B）越跑越慢（C）加速度越来越大（D）加速度越来越小答题： A. B. C. D.参考答案：C6. 6-24．点作曲线运动，若其法向加速度越来越大，则该点的速度____________。

第一篇静力学第1 章静力学公理与物体的受力分析1.1 静力学公理公理 1 二力平衡公理：作用于刚体上的两个力，使刚体保持平衡的必要和充分条件是：这两个力大小相等、方向相反且作用于同一直线上。

F=-F’工程上常遇到只受两个力作用而平衡的构件，称为二力构件或二力杆。

公理 2 加减平衡力系公理：在作用于刚体的任意力系上添加或取去任意平衡力系，不改变原力系对刚体的效应。

推论力的可传递性原理：作用于刚体上某点的力，可沿其作用线移至刚体内任意一点，而不改变该力对刚体的作用。

公理 3 力的平行四边形法则：作用于物体上某点的两个力的合力，也作用于同一点上，其大小和方向可由这两个力所组成的平行四边形的对角线来表示。

推论三力平衡汇交定理：作用于刚体上三个相互平衡的力，若其中两个力的作用线汇交于一点，则此三个力必在同一平面内，且第三个力的作用线通过汇交点。

公理4作用与反作用定律：两物体间相互作用的力总是同时存在，且其大小相等、方向相反，沿着同一直线，分别作用在两个物体上。

公理5 钢化原理：变形体在某一力系作用下平衡，若将它钢化成刚体，其平衡状态保持不变。

对处于平衡状态的变形体，总可以把它视为刚体来研究。

1.2 约束及其约束力１．柔性体约束２．光滑接触面约束３．光滑铰链约束第2章平面汇交力系与平面力偶系1.平面汇交力系合成的结果是一个合力,合力的作用线通过各力作用线的汇交点,其大小和方向可由失多边形的封闭边来表示,即等于个力失的矢量和,即FR=F1+F2+…..+Fn=∑F2.矢量投影定理：合矢量在某轴上的投影，等于其分矢量在同一轴上的投影的代数和。

3.力对刚体的作用效应分为移动和转动。

力对刚体的移动效应用力失来度量；力对刚体的转动效应用力矩来度量，即力矩是度量力使刚体绕某点或某轴转动的强弱程度的物理量。

（Mo（F）=±Fh）4.把作用在同一物体上大小相等、方向相反、作用线不重合的两个平行力所组成的力系称为力偶，记为（F,F’）。

第五章点的运动学本章将研究点的运动，包括点的运动方程、运动轨迹、速度、加速度等。

点的运动学也是研究刚体运动的基础。

第一节点的运动方程点在取定的坐标系中位置坐标随时间连续变化的规律称为点的运动方程。

点在空间运动的路径称为轨迹。

在某一参考体上建立不同的参考系，点的运动方程有不同的形式。

一、矢量法设点作空间曲线运动，在某一瞬时t ，动点为M，如图5-1所示。

选取参考体上某固定点O为坐标原点，自点O向动点M作矢量r，称r为点M相对于原点O的矢径。

当动点M运动时，矢径r随时间而变化，并且是时间的单值连续函数，即(5-1)上式称为矢量形式表示的点的运动方程。

显然，矢径r的矢端曲线就是动点的运动轨迹。

图5-1二、直角坐标法过点O建立固定的直角坐标系Oxyz，则动点M在任意瞬时的空间位置也可以用它的三个直角坐标x , y , z表示，如图5-1所示。

由于矢径的原点和直角坐标系的原点重合，矢径r可表为(5-2)式中i , j , k 分别为沿三根坐标轴的单位矢量。

坐标x , y , z也是时间的单值连续函数，即(5-3)式(5-3)称为点的直角坐标形式的运动方程，也是点的轨迹的参数方程。

三、自然法当动点相对于所选的参考系的轨迹已知时，可以沿此轨迹确定动点的位置。

在轨迹上任取固定点O 作为原点，选定沿轨迹量取弧长的正负方向，则动点的位置可用弧坐标s 来确定。

如图5-2所示。

动点沿轨迹运动时，弧长s 是时间的单值连续函数(5-4)上式称为点用自然法描述的运动方程。

图5-2以上三种形式的运动方程在使用上各有所侧重。

矢量形式的运动方程常用于公式推导；直角坐标形式的运动方程常用于轨迹未知或轨迹较复杂的情况；当轨迹已知为圆或圆弧时，用自然法则较为方便。

第二节点的速度和加速度动点运动的快慢和方向用速度表示，速度的变化情况则用加速度表示。

下面给出在各坐标系下，速度、加速度的数学表达式。

一、用矢量法表示点的速度和加速度如动点矢量形式的运动方程为r=r(t) ，则动点的速度定义为（5-5）即动点的速度等于动点的矢径r对时间的一阶导数。

1第六章点的运动学1．点以匀速率沿阿基米德螺线由外向内运动，如图所示，则点的加速度（则点的加速度（）。

① 不能确定不能确定② 越来越小越来越小③ 越来越大越来越大④ 等于零等于零正确答案：③2．动点M 作曲线运动，某瞬时点的速度v = 4m/s ，点的切向加速度，点的切向加速度 τa = - 2m/s 2，一秒钟后点的速度大小用v 1表示，则（表示，则（）。

① v 1 = 4m/s ②v 1 = 2m/s ③ v 1 = 6m/s ④v 1 无法确定无法确定 正确答案：④3．动点M 沿其轨迹运动时，下列几种情况中，正确的应该是（沿其轨迹运动时，下列几种情况中，正确的应该是（）。

① 若始终有v ⊥ a ，则必有v 的大小等于常量的大小等于常量② 若始终有v ⊥ a ，则点M 必作匀速圆周运动必作匀速圆周运动③ 若某瞬时有v // a ，则点M 的轨迹必为直线的轨迹必为直线④ 若某瞬时有a 的大小等于零，且点M 作曲线运动，则此时速度必等于零作曲线运动，则此时速度必等于零 正确答案：①4．点的切向加速度与其速度（．点的切向加速度与其速度（ ）的变化率无关，而点的法向加速度与其速度（）的变化率无关，而点的法向加速度与其速度（ ）的变化率无关。

无关。

① 大小大小 ② 方向方向正确答案： ② ①5．点作曲线运动时，“匀变速运动”指的是（“匀变速运动”指的是（）。

① a τ= 常矢量常矢量 ② a τ= 常量常量③ a = 常矢量常矢量 ④ a = 常量常量正确答案： ②6．绳子的一端绕在滑轮上，另一端与置于水平面上的物块B 相连，若物块B 的运动方程为x = kt 2，其中k 为常数，轮子半径为R ，则轮缘上A 点的加速度的大小为（点的加速度的大小为（）。

① k 2② 21222)/4(R t k③ 212442)/164(R t k k +④ R t k k /4222+正确答案： ③27．点作曲线运动时，法向加速度等于零的情况，可能是（．点作曲线运动时，法向加速度等于零的情况，可能是（）或（）或（ ）。