江西财经大学数学社2015年下学期第一次讲义

━━━━━━━━江西财经大学试卷━━━━━━试卷代码:E2443A 课程学时:48课程名称:市场营销学适用对象:挂牌━━━━━━━━━━━━━━━━━━━━━━━━一、选择题（每小题1分，共10分）[1—5单项选择题，6—10多项选择题][在答题纸上写明各小题题号，并在其后写出答案]1、产品组合的关联性是指①部分产品项目之间的关联性程度②一个企业产品线的多少③各产品线在最终用途、生产条件、销售渠道等方面的相关程度④一个企业成套设备的先进程度2、在产品进入成熟期后，总的发展趋势是①销售增长率下降，利润率上升②销售额持平，利润额下降③销售额缓慢上升，利润额持平④销售增长率和利润率均趋于下降3、市场占有率是指①在特定的空间范围内，本企业的某种产品的产量在同类产品总产值中所占比例②在特定的空间、时间范围内，企业的某种产品销量在同类产品总销量中所占的比例。

③在特定的时、空范围内，企业所有的顾客数量。

④在特定的时、空范围内，企业某种产品与主要竞争对手同类产品之间的比例。

4、在特定市场区域内出现的所有市场机会，对某个（些）企业来说①都具有同等的吸引力②并非都具有同等吸引力③均可转化为该企业的营销机会④都能使企业获取差别利益5、对许多异质性产品而言，影响消费者购买行为的诸因素中①经济因素常起决定作用②社会文化因素和个人心理、个性等因素的作用比经济因素的作用更为重要③购买者的年龄、性别、职业等因素常起决定作用④政治因素与群体因素起决定作用6、需求价格弹性的大小，主要取决于①商品的需要程度②收入弹性③商品的替代性④商品供求状况⑤商品的销售数量7、属直接分销渠道的销售形式有①前店后厂②邮购③电话营销④展销会⑤零售商8、在下列备选答案中，属于广告媒体范畴的是①广告公司②报纸、杂志③霓虹灯④商品目录⑤路牌9、营业推广促销活动的主要方式包括①进行营销性宣传，并辅之以各种附和利益②利用大众传播媒介传递产品信息，制造舆论，创造适销环境③利用推销人员直接与顾客接触，排疑解难，说服购买④通过与社会大众建立相互信任的和睦关系，达到扩大产品销售的目的⑤通过举办或参加产品展销会、博览会等活动，吸引顾客，达到扩大销售的目的10、差异性市场营销策略是企业有意识地①、抓住各细分市场的需求个性，放弃共性的目标营销策略②、抓住各细分市场的需求共性，而放弃个性的目标营销策略③、以所有细分市场作为目标市场的营销策略④以部分细分市场作为目标市场的营销策略⑤为各细分市场分别制定营销方案的目标营销策略二、判断题（每小题1分，共10分）[在答题纸上写明各小题题号，并在其后写出答案]1、实行高价策略是企业获取最大利润的主要途径。

第三篇 概率统计第一讲 事件与概率考纲要求1.了解样本空间（基本事件空间）的概念，理解随机事件的概念，掌握事件的关系及运算.2.理解概率、条件概率的概念，掌握概率的基本性质，会计算古典型概率和几何型概率，掌握概率的加法公式、减法公式、乘法公式、全概率公式以及贝叶斯（Bayes ）公式.3.理解事件独立性的概念，掌握用事件独立性进行概率计算；理解独立重复试验的概念，掌握计算有关事件概率的方法.一、事件运算与关系问题1 何谓样本空间？何谓随机事件？答 随机试验的所有可能结果组成的集合称为该试验的样本空间，样本空间的元素称为样本点.样本空间的子集称为随机事件. 样本空间称为必然事件，空集称为不可能事件，只含一个样本点的子集称为基本事件.由于随机事件是样本空间的子集，因此可以用集合方法研究事件.问题2 叙述事件的关系与运算.答 事件的关系与运算有A B A B B A ⊂⑴包含：若发生必导致发生，则称包含于，记作；A B B A A B A B =⑵相等：若包含于且包含于，则称与相等，记作；⑶和事件：“A 与B 至少发生一个”称为A 与B 的和事件，记作；A B ∪A ⑷积事件：“与B 同时发生”称为A 与B 的积事件，记作或者A B ∩AB ；AB A B A B A B −⑸差事件：“发生，不发生”称为与的差事件，记作或者；A A A ⑹逆事件(对立事件)：“不发生”称为的逆事件或者对立事件，记作；⑺互不相容（互斥）：若A 与B 不能同时发生，则称A 与B 互不相容或者互斥，记作； AB =∅⑻完备事件组：若，12n A A A Ω=∪∪ ∪(1)i j A A i j n =∅≤<≤，则称为完备事件组；12,,,n A A A A B ⑼与相互独立：；()()()P AB P A P B =⑽个事件相互独立：其中任意n 12,,,n A A A (2)k k n ≤≤个事件的积的概率等于它们的概率之积.问题3 叙述事件的运算律.答 事件的运算律就是集合的运算律，主要有A B B A =∪∪AB BA =⑴交换律：，；⑵结合律：()A ()B C A B C =∪∪∪∪()()AB C A BC =；，⑶分配律：()()(A B C AB AC )=∪∪()()()A BC A B A C =∪∪∪； ，A B A B =∪∩A B A B =∩∪⑷对偶律：，.问题4 证明下列关于独立性的命题： A B A B A B B A 独立.与独立，则与，与，与⑴若A B A B ⑵当，时，若()0P A >()0P B >不独立.与互斥，则与A B ⊂A B ⑶当时，若()0,()1P A P B ><不独立.，则与⑷概率为（或者概率为1）的事件与任一事件0A 独立，特别，不可能事件与任一事件∅A 独立，必然事件与任一事件A Ω独立.⑸若个事件相互独立，则它们两两独立，其逆命题不成立.n 12,,,n A A A 例B A AB =1.设为随机事件，且满足B A ,，则（）.【B 】(A) (B)A B =∅∪=B A ∪A B A =∪B B A =∪Ω (C) (D)2.对于任意二事件A 和B ，与不等价的是（）.【D 】B B A =∪(A)B A ⊂ (B)A B ⊂AB =∅ (C) (D)AB =∅3.设为两事件，且B A ,0)(=AB P ，则（）.【C 】A B 互斥 (B)AB 是不可能事件(A)与AB (C)未必是不可能事件 (D)或0)(=A P 0)(=B P【注 概率为零的事件不一定是不可能事件】0()1,()(P B P A B P A B <<=)4.设为两事件,且B A ,，则（）.【C 】B A = (C)A 与(A) (B)AB =∅B 相互独立 (D)A B ⊂ .A B 5.对于任意二事件，有（）.【B 】和(A)若,则一定独立 (B)若AB ≠∅AB ≠∅B A ,,则有可能独立B A ,(C)若则一定独立 (D)若AB =∅AB =∅B A ,,则一定不独立B A ,=1A 6.将一枚硬币独立地掷两次，引进事件：{第一次出现正面}，{第二次出现正面}，{正、反各出现一次}，{正面出现两次}，则事件（）.【C 】=2A =3A =4A (A)相互独立 (B)相互独立321,,A A A 432,,A A A (C)两两独立 (D)两两独立321,,A A A 432,,A A A 二、古典概型与几何概型问题5 如何计算古典型概率？()A n P A n =A Ω答 若样本空间仅包含有限个等可能的样本点，则任一事件的概率，其中n 为包含的样本点数，为A n A Ω包含的样本点数.常用计数方法：分类用加法，分步用乘法，有序用排列，无序用组合，穷举法.常犯的错误是计算样本点数时漏算和多算.问题6 如何计算几何型概率？()A s P A s=答 若样本空间Ω包含无限个等可能的样本点，则任一事件A 的概率，其中为的度量（长度、面积、体积），为s A s A Ω的度量. 例1.袋中装有10个球，其中红球6个，白球4个，从中任取3个球，则至少取到两个红球的概率为 213646310C C C C +.【】 2. 袋中装有6个球，其中红球1个，白球2个，黒球3个，从中每次取一个，取后放回，共取两次，则取到1个白球、1个黒球的概率为 13.【】 3.袋中装有10个球，其中红球6个，白球4个，两人依次随机从中各取1个球，取后不放回，则第二个人取到红球的概率为 .【0.6，抽签原理】4.一间宿舍内住有6位同学，求他们之中恰有4个人生日在同一月份的概率.4266121112C ⋅⋅】 【235.将3封信随机装入3个写好地址的信封内，则至少有一封装对的概率为 .【】 5126.掷两枚骰子，则它们的点数之和小于7的概率为 .【】7.一个陀螺的半圆周上均匀刻有[0内的数字，另半圆周上均匀刻有[1内的数字，则当它停止旋转时，着地点落在[内的概率为 ,1],3]0.5,1.5].【38】 3t 8.两个信号在[0内随机到达某接收装置，若它们到达的时间间隔小于,]t ，则发生干扰，求它们发生干扰的概率.【会面问题，59】 三、概率计算公式问题7 何谓加法公式？答 .加法公式：.()()()()P A B P A P B P AB =+−∪由加法公式可得：A B 互不相容时，；()()()P A B P A P B =+∪与⑴当()1()P A P A =−； ⑵()()()()()()()()P A B C P A P B P C P AB P AC P BC P ABC =++−−−+∪∪⑶（公式特点：加奇减偶. 可以推广到有限个事件的情形）.()()(P A B P A P AB )−=−；⑷.减法公式：B A ⊂()()(P A B P A P B )−=−.⑸当时，问题8 何谓条件概率？如何计算条件概率？(P B A )A B 答 事件发生的条件下，事件发生的概率称为条件概率. 计算条件概率的方法有：()()()P AB P B A P A =，其中. ()0P A >⑴利用条件概率公式A 发生的条件下的样本空间）⑵缩小样本空间（考虑事件问题9 叙述乘法公式、全概率公式和贝叶斯公式.()()()()()P AB P A P B A P B P A B ==,A B 答 1.乘法公式：对于任意两个事件； ，有()()()()P ABC P A P B A P C AB =,,A B C 对于任意两个事件，有（可以推广到有限个事件的情形）.2.全概率公式：若是一个完备事件组，则对任一事件12,,,n A A A B ，有11()()()()n ni i i i P B P A B P A P B A ====∑∑i .3.贝叶斯公式：若是一个完备事件组，且，则有12,,,n A A A ()0P B >1()()()()(1,2,,()()()i i i i n i i i P A P B A P A B P A B i n P B P A P B A ====∑ ). 【注】 全概率公式在概率计算中是十分重要的，它利用完备事件组将事件12,,,n A A A B 分解为个互斥事件之和，然后利用加法公式和乘法公式计算其概率. 运用全概率公式计算事件的概率，关键是构造完备事件组，常用的完备事件组有：n 12,,,n A B A B A B A A ⑴与；取它的一切可能值{}(1,2,i X x i == )X ；⑵离散随机变量(1,2,)i A i = B .⑶伴随事件发生的一切可能的情形()0,()1P B P A B >例1. 设为两事件,且，=))))>B A ,则必有（）.【C 】(A) (B)()(P A B P A >∪()(P A B P B >∪(C) (D)()(P A B P A =∪()(P A B P B =∪2. 设为两事件,且，则必有（）.【B 】B A ,,()0A B P B ⊂()()P A P A B <()()P A P A B ≤()()P A P A B >()()P A P A B ≥ (B) (C) (D)(A)3.设5.0)(,9.0)()(==+B A P B P A P ∪，则=+)()(B A P B A P .【0.1】1114.100件产品中有10件次品，依次不放回地取出两件，则第二次才取得正品的概率为 .【】5.某厂生产的产品有70％可直接出厂，有30％需调试，其中调试后有80％可以出厂，20％定为不合格产品，现随机取一件，属于可出厂的产品，求该产品属于可直接出厂的概率.【0.74】6.每箱产品有10件，其次品数从0到2是等可能的，开箱检验时，从中任取一件，如果检验为次品，则认为该箱产品不合格而拒收，由于检验误差，一件正品被误判为次品的概率为2％，一件次品被误判为正品的概率为10％，求(1)检验的一箱能通过验收的概率；(2)检验10箱产品通过率不低于90％的概率.解 ⑴设表示“取到的一箱中有i 件次品”，i A B 表示“开箱检验时取到正品”，表示“检验的一箱能通过验收”.C 由全概率公式，00112()()()()()()()P B P A P B A P A P B A P A P B A =++211019180.9310310310=×+×+×=； ()()()()()0.90.980.10.10.892P C P B P C B P B P C B =+=×+×=X (10,)X B p ∼()0.892p P C ==⑵设表示“通过验收的箱数”，则，其中，{}{}{0.9991010X P P X P X P X ⎧⎫≥=≥==+=⎨⎬⎩⎭} 9910100.8920.1080.8920.705C =⋅+=.问题10 何谓二项概率公式？答 设事件A 在一次试验中出现的概率为，则次重复独立试验中，事件n p A 恰好出现次的概率，此公式称为二项概率公式.k ()(1)(0,1,,)k k n k n n P k C p p k n −=−= 例1. 设事件A 在一次试验中出现的概率为(01)p p <<，则次重复独立试验中，事件n A 至少出现一次的概率为 .2.甲乙两人进行乒乓球单打比赛，甲每局获胜的概率为，若采用五局三胜制，则甲获胜的概率为 0.6. 注意：第二讲 随机变量及其分布考纲要求{}()()F x P X x x =≤−∞<<∞1.理解随机变量的概念；理解分布函数的概念及性质；会计算与随机变量相联系的事件的概率.01−2.理解离散型随机变量及其概率分布的概念，掌握分布、二项分布、超几何分布、泊松（Poisson ）分布及其应用.3.了解泊松定理的结论和应用条件，会用泊松定理近似计算二项分布.2(,)N μσ4.理解连续型随机变量及其概率密度的概念，掌握均匀分布、正态分布、指数分布及其应用.5.会求随机变量函数的分布.一、随机变量与分布函数问题1 何谓随机变量？ωX Ω答 如果对于样本空间中的每一个样本点（试验结果），变量都有一个确定的实数值与之对应，则称X ()X X ω=.为随机变量，记作▲随机变量是一个定义在样本空间上的实值函数.Ω问题2 分布函数的概念与性质.{}()()F x P X x x =≤−∞<<∞X 答 函数的分布函数.称为随机变量X X (,]x −∞内的概率.的分布函数就是的取值落在区间▲随机变量分布函数具有如下性质：()F x ⑴0(；)F x ≤≤101⑵，()F −∞=()F +∞=；⑶单调不减； ()F x⑷右连续即()F x (,x )∀∈−∞+∞()(0)F x F x =+，；{}()()P a X b F b F a <≤=−；⑸{}()(0)P X a F a F a ==−−⑹.▲离散随机变量的分布函数为阶梯函数，每个可能值是它的跳跃间断点；连续随机变量的分布函数()i i x x F x p ≤=∑()()xF x f x d −∞=∫)x 为(,−∞+∞上的连续函数.例题1.下列各函数中，可以作随机变量分布函数的是（）.【C 】211)(xx F +=x x F arctan 2)(π= （B ） （A ）0,0,(),01x F x x x x≤⎧⎪=⎨>⎪+⎩π2arctan )(+=x x F （C ） （D ） 2.设与分别是随机变量与的分布函数.为使)(1x F )(2x F 1X 2X )()()(21x bF x aF x F −=是某一随机变量的分布函数，在下列给定的各组数中应取（）.【A 】52,53−==b a 32,32==b a 23,21=−=b a 23,21==b a （B ） （C ） （D ） （A ）0,1/8,(),1,F x ax b ⎧⎪⎪=⎨+⎪⎪⎩1,1,111.x x x x ,<−=−−<<≥41}1{==X P X 3.设随机变量， 的分布函数为又已知则（）.【A 】167,165==b a 169,167==b a 21,21==b a 83,83==b a （B ） （C ） （D ） （A ）X 注 本题中的随机变量既非离散、也非连续随机变量，因为其分布函数不是阶梯函数，又有两个间断点.问题3 叙述离散型随机变量及其概率分布的定义.X X 答 若随机变量是离散型随机变量.只取有限个或者可列无穷个值，则称{}(1,2,i i P X x p i === 若随机变量X 的取值为，则称12,,x x )X 的概率分布. 为求离散随机变量的概率分布，关键是确定它取哪些值，求出对应概率.X 的概率分布具有如下性质：随机变量⑴；0,1,2,i p i ≥= ⑵.1i i p=∑例1.设随机变量X 的分布律为，则常数⎟⎟⎠⎞⎜⎜⎝⎛−−c c c 839102=c X 的分布函数 ，=)(x F .0,0.4,()0.8,1,F x ⎧⎪⎪=⎨⎪⎪⎩,3,31,11,1≥<≤<≤−−<x x x x X X 2.设随机变量 则的概率分布为 的分布函数为.00,()2/301,1 1.x F x x x <⎧⎪=≤<⎨⎪≥⎩，，，13c =3X 1−1 答案 1. 2. ；0.40.40.2P问题3 何谓连续型随机变量？连续型随机变量的概率密度具有哪些性质？答 若存在非负函数()f x ，使得随机变量X 的分布函数，则称()()x F x f x dx −∞=∫X 为连续型随机变量，并称X ()f x 的概率密度或者密度函数.为概率密度具有如下性质性质：⑴；()0f x ≥()1f x dx +∞−∞=∫⑵；⑶连续；()()xF x f x dx −∞=∫x ⑷若()f x 在点连续，则；()()F x f x ′=⑸；{}()()()b a P a X b F b F a f x dx <≤=−=∫{}0P X a ==.⑹例 1.设和是任意两个相互独立的连续型随机变量，它们的概率密度分别为和1X 2X )(1x f)(2x f ，分布函数分别为和，则（）.【C 】)(1x F )(2x F （A ） +必为某一随机变量的概率密度)(1x f )(2x f （B ） +必为某一随机变量的分布函数)(1x F )(2x F （C ） 必为某一随机变量的分布函数)(1x F )(2x F （D ） 必为某一随机变量的概率密度)(1x f )(2x f X X 2.已知连续型随机变量的概率密度是偶函数,是)(x f )(x F 的分布函数，则对任意常数,有（）.【B 】c =−)(c F ∫−c dx x f 0)(21 (D) ∫−c dx x f 0)(1（A ） （B ）)(c F 1)(2−c F （C ）1/3,()2/9,0f x ⎧⎪=⎨⎪⎩else x x ],6,3[],1,0[∈∈32}{=≥c X P 若c 使得3.设随机变量X 的概率密度为，则的取值范围是 c .【13】c ≤≤2,()0,x f x ⎧=⎨⎩)1,0()1,0(∉∈x x X }{}{a X P a X P ≤=≥,则= a 4.随机变量的概率密度为若.【2a =】 X X X −5.设连续型随机变量的分布函数为，密度函数为，若)(x F )(x f 与有相同的分布函数，则（）.【C 】)()(x F x F −=)()(x F x F −−=)()(x f x f −=（A ） （B ） （C ） (D) )()(x f x f −−=问题4 如何求随机变量函数的概率分布？X X 答 设在随机变量()g x ()Y g X =的函数. 的一切可能值有定义，则称为随机变量()Y g X =取哪些值，并求出对应的概率； 求离散型随机变量函数的分布，关键是：弄清()Y g X =的取值范围，并求出分布函数.求连续型随机变量函数的分布，关键是：弄清121344⎛⎞⎜⎟⎜⎟⎝⎠101~111244X −⎛⎞⎜⎟⎜⎟⎝⎠12+=X Y 例1.设随机变量的概率分别为 ，则.【】 2.设随机变量X 服从参数为2的指数分布,求的概率密度.X e Y 21−−=解 X 的概率密度 22,0()0,0.x e x f x x −⎧>=⎨≤⎩,X 的取值范围(0,)+∞，的取值范围为(0.21X Y e −=−,1){}()Y F y P Y y =≤3X Y =，的分布函数{}()0Y F y P Y y =≤={}()1Y F y P Y y =≤=当时，0y ≤，当时，1y ≥， 当01时，y <<{}{}21()1ln(1)2X Y F y P Y y P e y P X y −⎧⎫=≤=−≤=≤−−⎨⎬⎩⎭11ln(1)ln(1)2220()2y y x f x dx e dx y −−−−−−∞==∫∫=，所以，的概率密度为1,(0,1),()()0,(0,1).Y Y y f y F y y ∈⎧′==⎨∉⎩21X Y e −=−1,()0,x f x ⎧−=⎨⎩.,11else x <<−12+=X Y X 求随机变量3.设随机变量的密度函数为的分布函数与密度函数.【1,0,−⎩12.y else <<,()Y f y =】问题5 有哪些常见分布？它们有哪些应用？ 答 常见分布有 1.分布01−{}1(1)(0,1)kkP X k p p k −==−=若X 的概率分布为，则称X 服从参数为的分布.01−p 2.二项分布{}(1)(0,1,,)kkn kn P X k C p p k n −==−= 若X 的概率分布为，则称X 服从参数为，p 的n~(,)X B n p .二项分布，记作最可能值，当0[(1)]k n p =+(1)n p +不是整数时；0(1),(1)k n p n p 1=++−，当是整数时.(1)n p +用于研究次重复独立试验中事件n A 出现的次数. 3.超几何分布{}(0,1,,m n m M N MnNC C P X m m n C −−=== )X X 若的概率分布为，则称服从参数为的超几何分布.,,n N M 用于研究不放回抽样. 4.几何分布{}1(1)(1,2,)k P X k p p k −==−= X X 服从参数为的几何分布.p 若的概率分布为，则称A 首次出现的试验次数. 用于研究重复独立试验中事件5.泊松（Poisson ）分布{}(0,1,2,!k P X k e k k λλ−=== λ)X X 若的概率分布为，则称服从参数为的泊松分布，记作~()X P λ.λλ0[]k λ=0,k 1λλ=−是整数时. ，当不是整数时；，当最可能值用于研究二项分布的极限.(1)!k k kn knC p p e k λλ−−−≈注 当n 很大，很小，p np λ=（泊松定理）； 时，(1)(m n m m m n mM N M n nN C C M C p p p C N−−−≈−=当很大，很小时，n N . 6.均匀分布1,[,]()0,[,],,x a b f x b ax a b ⎧∈⎪=−⎨⎪∉⎩若X 的概率密度为 则称X 服从区间[,上的均匀分布. ]a b 用于研究一维几何概率.7.指数分布若X 的概率密度为 则称,0()0,0,x e x f x x λλ−⎧>=⎨≤⎩,λX 的指数分布.服从参数为用于研究寿命、可靠性.8.正态分布22()2()x f x μσ−−=2σX X μ 则称的概率密度为服从参数为，的正态分布，记作若2~(,)X N μσ；当0μ=，1σ=X 时，则称服从标准正态分布，记作，其概率密度~(0,1)XN 22()x f x −=，分布函数记作()x Φ. 2~(,)X N μσ，则 设{}()(b a P a X b μμΦΦσσ−−<<=−；⑴⑵()1()x x ΦΦ−=−；⑶，(0)0.5Φ=(1.96)0.975Φ=； {}{}0.5P X P X μμ≤=≥=.⑷正常状态下，产品的产量指标、质量指标、测量误差服从正态分布.例1.一汽车沿一街道行驶，需要通过三个设有红绿灯的路口，各不同路口灯的显示情况相互独立，且每个路口上红、绿灯显示的时间比为1∶2，以X 表示该汽车驶过这条街道途中所遇到的红灯数，求1~(3,3X B X 的概率分布和分布函数.【】223e −X }2{}1{===X P X P ==}4{X P 2.设随机变量 服从泊松分布，且，则.【】 3.假设一大型设备在任何长为t 的时间内发生故障的次数服从参数为)(t N t λ的泊松分布. ⑴求相继两次故障之间时间间隔T 的概率分布；⑵求在设备已无故障工作8小时的情形下，再无故障运行8小时的概率. {}()F t P T t =≤解 ⑴T 的取值范围为，T 的分布函数(0,)+∞， {}()F t P T t =≤当时，0t ≤＝0；{}{}{}()11()01tF t P T t P T t P N t eλ−=≤=−>=−==−当时，0t >.{}{}{}{}{}168816,8161(1)168881(1)P T T P T e P T T e P T P T e λλλ−−−≥≥≥−−≥≥====≥≥−− ⑵.4.设随机变量，则2~(2,),{24}0.3X N P X σ<<==<}0{X P . 【0.2】211~(,)X N μσ222~(,)Y N μσ5.设随机变量，且，1{1}{P X P Y μ−≤>−≤21}μ2则必有（ ）. 【A 】（A ）1σσ<（B ）12σσ>（C ）12μμ<12μμ>（D ） 1001=λ6..已知某类电子元件使用寿命（小时）服从参数为的指数分布.现有10个此类元件独立工作，求这10个元件中，至少有一个元件的寿命小于50小时的概率.【】 51e −−第三讲 二维随机变量的概率分布考纲要求1.理解多维随机变量的概念，理解多维随机变量的分布的概念和性质，理解二维离散型随机变量的概率分布、边缘分布和条件分布，理解二维连续型随机变量的概率密度、边缘密度和条件密度，会求与二维随机变量相关事件的概率.2.理解随机变量的独立性及不相关的概念，掌握随机变量相互独立的条件.3.掌握二维均匀分布，了解二维正态分布的概率密度，理解其中参数的概率意义.4.会求两个随机变量简单函数的分布，会求多个相互独立随机变量简单函数的分布.一、二维随机变量的概率分布问题1 何谓二维随机变量的联合分布函数？何谓二维随机变量的边缘分布函数？{}(,),F x y P X x Y y =≤≤答 1.二维随机变量的联合分布函数),(Y X ，即的取值落在无穷矩形域),(Y X (,](,]x y −∞×−∞内的概率.二维随机变量的联合分布函数具有如下性质： ⑴0(；,)F x y ≤≤11⑵，(,)(,)(,)0F F y F x −∞−∞=−∞=−∞=(,)F +∞+∞=； x ⑶关于(,)F x y （关于）单调不减；yx ⑷关于(,)F x y y （关于）右连续. 2.二维随机变量关于),(Y X X 的边缘分布函数{}{}(),(,)lim (,)X y F x P X x P X x Y F x F x y →+∞=≤=≤<+∞=+∞=.二维随机变量关于Y 的边缘分布函数),(Y X {}{}(),(,)lim (,)Y x F y P Y y P X Y y F y F x y →+∞=≤=<+∞≤=+∞=.问题2 何谓二维离散型随机变量联合分布、边缘分布和条件分布？ 答 ⑴联合分布设二维离散随机变量(,)X Y 的所有可能值为(,),,1,2,i j x y i j = ，则称{},(,1,i j ij P X x Y y p i j ==== 2,)(,)X Y 的联合分布律，其中为二维离散随机变量01ij p ≤≤111ij i j p ∞∞===∑∑.，⑵边缘分布 称，{}1(1,2,)i iji j P X x pp i ∞⋅=====∑ {}1(1,2,j ij j i P Y y p p j ∞⋅=====∑ )X 和关于Y 的边缘分布律. (,)X Y 分别为关于利用联合概率分布表计算如下：⑶条件分布称{}(1,2,)iji j j p P X x Y y i p ⋅==== 为在j Y y =的条件下随机变量X 的条件分布；称{}(1,2,ijj i i p P Y y X x j p ⋅==== )为在i X x =的条件下随机变量Y 的条件分布.例λX 1.设某班车起点站上客人数服从参数为的泊松分布，每位乘客在中途下车的概率为且中途下车与否相互独立. 以Y 表示在中途下车的人数，求p ⑴在发车时有个乘客的条件下，中途有个人下车的概率；n m ⑵二维随机变量的概率分布(01-1).),(Y X {}(1)m mn m n P Y m X n C p p −===−解 ⑴；⑵二维随机变量的概率分布为),(Y X {}{}{},P X n Y m P X n P Y m X n ======(1)(0,1,2,0,1,,)!n m m n m n e C p p n m n n λλ−−=−== 2.设随机变量X 和Y 相互独立，下表列出了二维随机变量的联合概率分布及关于),(Y X X 和关于Y 的边缘概率分布的部分数值，将其余数值填入表中的空白处.解 由联合分布与边缘分布的关系，得111116824p =−=； 由独立性，得11112464p ⋅=÷=； 由概率分布的性质，得213144p ⋅=−=；其余数值可类似求出.故1x 1/24 1/8 1/12 1/4 2x1/8 3/8 1/4 3/4 }{j y Y P =1/6 1/2 1/313.设随机变量且满足101~(11/41/21/4i X i −⎛⎞=⎜⎟⎝⎠,2){}1201P X X ==，则{}12P X X == . 【0】问题3 何谓二维连续型随机变量的联合密度？它具有哪些性质？ (,)f x y ，使得随机变量(,)X Y 的分布函数答 若存在非负函数(,)(,)xyF x y f x y dxdy −∞−∞=∫∫(,)X Y (,)f x y (,)X Y ，则称为二维连续随机变量，并称为的联合概率密度或者联合密度函数.联合概率密度具有如下性质：⑴； (,)0f x y ≥(,)1f x y dxdy +∞+∞−∞−∞=∫∫⑵；⑶连续；(,)(,)x yF x y f x y dxdy −∞−∞=∫∫(,)(,)xyF x y f x y ′′=(,)f x y (,)x y 在点连续，则； ⑷若{}(,)(,)DP X Y D f x y dxdy ∈=∫∫.⑸2(),(,)0,x y ce f x y −+⎧=⎨⎩.,0,0else y x +∞<<+∞<<例1.设二维随机变量的概率密度),(Y X则常数 =c {(,)1}D x y x y =+≤；落在区域),(Y X 内的概率为 .2()0(,)41x y f x y dxdy dx e dy +∞+∞+∞+∞−+−∞−∞==∫∫∫∫=c 4；【提示：由推出{}112()20(,)413xx y P X Y D dx e dy e −−+−∈==−∫∫.】问题4 如何求二维随机变量的边缘密度？答 设(,)X Y (,)f x y ，则可按如下公式计算边缘密度： 的概率密度为()(,)X f x f x y +∞−∞=∫dy X ； 关于的边缘密度()(,)Y f y f x y +∞−∞=∫dx 关于Y 的边缘密度.26,,(,)0,x y x f x y else⎧≤≤=⎨⎩X 例 设二维随机变量的概率密度),(Y X 则关于),(Y X 的边缘概率密度 =)(x f X =)(y f Y ，关于Y 的边缘概率密度 .(,)f x y 解 画出概率密度的非零区域. X 的取值范围[0， ,1]由图看出，当0122()(,)66()xX xf x f x y dy dy x x +∞−∞===∫∫x ≤≤−，时，关于X 的边缘概率密度26(),01,()0,.X x x x f x else ⎧−≤≤=⎨⎩),01,()0,.Y y y f y else ⎧−≤≤⎪=⎨⎪⎩类似可求出关于Y 的边缘概率密度问题5 如何求二维随机变量的条件密度？(),()X Y f x f y 答 设(,)X Y (,)f x y ,X Y 的概率密度为，关于的边缘密度分别为，则可按如下公式计算条件概率密度：(,)()()X Y Y f x y f x y f y =X 在Y 的条件下，y =； 的条件概率密度(,)()()Y X X f x y f y x f x =在的条件下，Y 的条件概率密度X x =.问题6 如何判断随机变量的独立性？ 答 判断随机变量的独立性的方法有：⑴随机变量X 与Y 相互独立； (,)()()X Y F x y F x F y ⇔=X 与Y 相互独立,,ij i j i j p p p ⋅⋅⇔∀=； ⑵离散型随机变量(,)()()X Y f x y f x f y ⇔=X 与Y 相互独立. ⑶连续随机变量问题7 何谓二维均匀分布？1,(,),(,)0,(,),x y D f x y x y D σ⎧∈⎪=⎨⎪∉⎩答 若二维随机变量(,)X Y 的概率密度 其中σ为的面积，则称(,D )X Y 服从区域上的均匀分布.D 问题8 何谓二维正态分布？它具有哪些性质？ 答 若二维随机变量(,)X Y 的概率密度2(,)f x y ]⎧⎫=⎬⎭ 221212(,)~(,,,,)X Y N μμσσρ(,)X Y . 则称服从二维正态分布，记作221212(,,,,N )μμσσρ具有如下性质： 二维正态分布211(,)N μσ222(,)N μσX 和Y 的边缘分布分别为；⑴关于，⑵条件分布均为正态分布；aX bY +X 和Y 的非零线性组合服从正态分布； ⑶X 和Y 相互独立的充要条件是相关系数0ρ=.⑷例 设两个相互独立的随机变量X 和Y 分别服从正态分布和，则（ ）. )1,0(N )1,1(N 21}0{=≤+Y X P 21}1{=≤+Y X P (A) (B) 21}0{=≤−Y X P 21}0{=≤−Y X P (C) (D)【提示 独立的正态变量的线性函数仍为正态变量；B 】二、二维随机变量函数的分布问题9 如何求二维随机变量函数的概率分布？答 设在随机变量(,(,)g x y )X Y (,)Z g X Y =的一切可能值有定义，则称为随机变量(,)X Y 的函数.(,)Z g X Y =取哪些值，并求出对应的概率； 求离散型随机变量函数的分布，关键是：弄清(,)Z g X Y =的取值范围，并求出分布函数. 求连续型随机变量函数的分布，关键是：弄清X 与Y 的和Z X Y =+的概率密度，可用如下的卷积公式求两个独立随机变量()()()Z X Y f z f x f z x +∞−∞=−∫dx .例ηξ,ξ1.设是两个相互独立且服从同分布的随机变量，如果的分布律为3,2,1,31}{===i i P ξ),max(ηξ=X ),min(ηξ=Y 的分布律.，求与),max(ηξ=X 解 的取值为1，2，3{}{}{}{}111,1119P X P P P ξηξη========； {}{}{}{}321,11,22,29P X P P P ξηξηξη====+==+===； {}{}{}531129P X P X P X ==−=−==， ),max(ηξ=X 分布律为： 故X31 2P 1/93/95/9),min(ηξ=Y 分布律为：类似可求出 3Y 1 25/93/91/9P2.设和独立，1X 2X )2,1(1}2{,}1{=−====i p X P p X P i i ，令1,0,X ⎧=⎨⎩为偶数若为奇数若2121X X X X ++2X 的概率分布为 则. 02X1P2122p p −+222p p −}10,20),{(≤≤≤≤=y x y x D 3.设二维随机变量在矩形),(Y X 上服从均匀分布，试求边长为X 和Y 的矩形面积的概率密度.(99-1)S )(s f S 1,(,)(,)20,(,)x y Df x y x y D⎧∈⎪=⎨⎪∉⎩解 的概率密度),(Y X S XY =X 的取值范围为[0，Y 的取值范围为[0，,2],1]的取值范围为[0.,2]{}()S F s P S s =≤S XY =，的分布函数{}()0S F s P S s =≤={}()1S F s P S s =≤=当时，0s ≤，当时，2s ≥， 当02时，s <<{}{}{}()11S F s P S s P S s P XY s =≤=−>=−>211(,)1(1ln 2ln )22s s xxy ssf x y dxdy dx dy s >==−=+∫∫∫∫−， 1(ln 2ln ),02,()20,.S s s f s else ⎧−<<⎪=⎨⎪⎩故的概率密度S 2~(,)X N μσX 和Y 相互独立， Y X Z +=~(,)Y U ππ−， .试求4.设随机变量的密度函数（用表示）.(92-1))(x Φ2~(,)X N μσX 和Y 相互独立，~(,)Y U ππ−解 ，，1(),()()20,.X X Y f x y f x f y else πππ⎧−<<⎪=⎨⎪⎩，则的密度函数),(Y X =),(y x fY X Z +=的分布函数{}{}()(,)Z x y zF z P Z z P X Y z f x y dxd +≤=≤=+≤=∫∫y11()(22z y X z y dy f x dx dy ππππμΦππσ−−−∞−−−==∫∫∫z y t μσ−−=（令）1()()()22z z z z t dt t πμπμσσπμπμσσσΦσΦππ−−+−+−−−=−=∫∫dt ，Y X Z +=的密度函数1()()[]2Z Z z z f z F z πμππσσ+−−−⎛⎞⎛′==Φ−Φ⎜⎟⎜⎝⎠⎝μ⎞⎟⎠.第四讲 随机变量的数字特征考纲要求1.理解随机变量数字特征（数学期望、方差、标准差、矩、协方差、相关系数），会运用数字特征的基本性质，并掌握常用分布的数字特征.2.会求随机变量函数的数学期望.一、随机变量的数字特征问题1 叙述随机变量的数学期望的定义、性质及随机变量函数的数学期望公式. 答 随机变量的数学期望是随机变量的平均值，它反映随机变量取值的中心位置. 1.定义与公式{}(1,2,)i i P X x p i === i iiEX x p =∑X ,；⑴离散型随机变量的概率分布为{}(1,2,i i P X x p i === )X ，的概率分布为⑵离散型随机变量()()i i iEg X g x p =∑；{},(,1,i j ij P X x Y y p i j ==== ⑶二维离散型随机变量(,)X Y 2,)的概率分布为，(,)(,)i j ij ijEg X Y g x y p =∑∑；⑷连续型随机变量X 的概率密度为()f x ,；()EX xf x dx +∞−∞=∫⑸连续型随机变量X 的概率密度为()f x ,；()()()Eg X g x f x dx +∞−∞=∫(,)X Y (,)f x y ,⑹二维连续型随机变量的概率密度(,)(,)(,)Eg X Y g x y f x y dxdy +∞+∞−∞−∞=∫∫.2性质⑴；Ec c =⑵； EkX kEX =()E X c EX c +=+； ⑶()E X Y EX EY +=+⑷；()E XY EX EY =⋅X 与Y 相互独立，则⑸若； 问题2 叙述随机变量的方差的定义与性质.答 随机变量的方差反映随机变量取值的离散程度.1.定义 随机变量X 的方差2(DX E X EX =−). 2.性质 ⑴； ()0D c =⑵； 2()D kX k DX =⑶；()D X c DX +=()D X Y DX DY ±=+X 与Y 相互独立，则⑷若； ⑸.22()DX EX EX =−问题3 叙述随机变量的矩的定义.答 随机变量X 的阶原点矩，阶中心矩.k k k k a EX =()k k b E X EX =−显然，随机变量的数学期望是一阶原点矩，随机变量的方差是二阶中心矩. 问题4 如何求随机变量的数字特征？答 随机变量的数字特征是重点，也是常考点，读者务必在理解概念的基础上，熟练掌握计算数字特征的方法：⑴利用定义（6个公式）⑵用性质，计算时，要充分利用独立性条件.1,0,1,Y ⎧⎪=⎨⎪−⎩0,0,0,X X X >=<[]2,1−X 例 1.设随机变量则方差在上服从均匀分布，令随机变量98=DY ，提示：先求Y 的分布，再利用公式】22()DY EY EY =− .【2.已知甲、乙两箱中装有同种产品，其中甲箱中装有3件合格品和3件次品，乙箱中仅装有3件合格品.从甲箱中任取3件产品放入乙箱后，求：X 的数学期望；⑴乙箱中次品数23=EX 14⑵从乙箱中任取一件产品是次品的概率.【⑴p ⑵】 ,()0,ax b f x +⎧=⎨⎩]1,0[]1,0[∉∈x x 127=EX 3.设随机变量X ，则 =a 的概率密度为且已知，=b .1()()1f x dx ax b dx +∞−∞=+=∫∫17()()12xf x dx x ax b dx +∞−∞=+=∫∫】 ，【提示：X 4.设某种商品每周的需求量是服从区间上均匀分布的随机变量，而经销商店进货量为区间中的某一整数，商店每销售一单位商品可获利500元；若供大于求，则削价处理，每处理一单位商品亏损100元；若供不应求，则可以从外部调剂供应，此时每 ]30,10[]30,10[一单位商品仅获利300元,为使商店所获利润期望值不少于9280元，试确定最少进货量.1,1030,()200,.x f x else ⎧≤≤⎪=⎨⎪⎩X 解 服从区间上均匀分布，概率密度]30,10[ 设进货量为a ，则当10时，利润X a ≤≤500100()600100Y X a X X a =−−=− a 当时，利润30a X <≤500300()300200Y a X a X =+−=+ 600100,10,()300200,30,X a X Y g X X a a X a −≤≤⎧==⎨+<≤⎩故利润期望值301011()()(600100)(300200)2020aa EY g x f x dx x a dx x a +∞−∞==−++∫∫∫dx令，解得9280EY ≥21a =221()xx f x −+−=5.已知随机变量X 的概率密度函数，则EX = ，DX =.【1；12】 问题5 叙述协方差、相关系数的定义与性质 答1.协方差(,)()()Cov X Y E X EX Y EY =−−X 与Y 的协方差定义 随机变量. 协方差具有如下性质： ⑴； (,)(,)Cov X Y Cov Y X =(,)(,Cov aX bY abCov X Y )=⑵； ⑶；(,)(,Cov X k Y h Cov X Y ++=))⑷； (,)(,)(,)Cov X Y Z Cov X Y Cov X Z +=+⑸；(,)Cov X X DX =⑹； (,)Cov X Y EXY EX EY =−⋅⑺.()2(,D X Y DX DY Cov X Y ±=+±2.相关系数X 与Y 的线性相关程度.相关系数刻画两个随机变量XY ρ=0XY ρ=X 与Y 的相关系数. 若，则称随机变量定义 随机变量X 与Y 不相关.相关系数具有如下性质： 1XY ρ≤⑴；{}11XY P Y aX b ρ=⇔=+=，特别：若Y aX b =+⑵，则当时，0a >0a <1XY ρ=，当时，1XY ρ=−.问题6 设，证明下列命题等价： 0,0DX DY ≠≠X 与Y 不相关； ⑴⑵； (,)0Cov X Y =EXY EX EY =⋅⑶； ⑷. ()D X Y DX DY +=+XY ρ=证 由由知，命题⑵和⑶等价； (,)Cov X Y EXY EX EY =−⋅由知，命题⑵和⑷等价； ()2(,D X Y DX DY Cov X Y +=++)由等价关系的传递性知，这四个命题等价.问题7 随机变量的独立性与相关性有何关系？ X 与Y 独立，则X 与Y 一定不相关.答 若0XY ρ=⇒证明如下：X 与Y 独立EXY EX EY =⋅⇒(,)0Cov X Y =⇒X ，即与Y 一定不相关.若X 与不相关，则Y X 与不一定独立. 例如二维随机变量服从单位圆),(Y X Y }1),{(22≤+=y x y x G X 和Y 不相关，且X 与Y 不独立.上的均匀分布，则X 与Y 的联合分布为二维正态分布，则X 注意 若与独立的充要条件是Y X 与Y 不相关. 例{}213P X =={}123P X ==X 1.设随机变量与独立同分布，且Y X 的概率分布为，，，V 481max(,)U X Y =min(,)X Y ，求U 与V 的协方差.【(,)Cov U V =】 2π−)21(,0(2N Y X −2.设独立且都服从Y X ,的期望与方差.】，求3.对40个人的血液进行化验时，将每4个人并为一组化验一次，如果合格，则4个人只化验一次，若不合格，再对这组4个人逐个进行化验，共化验5次。

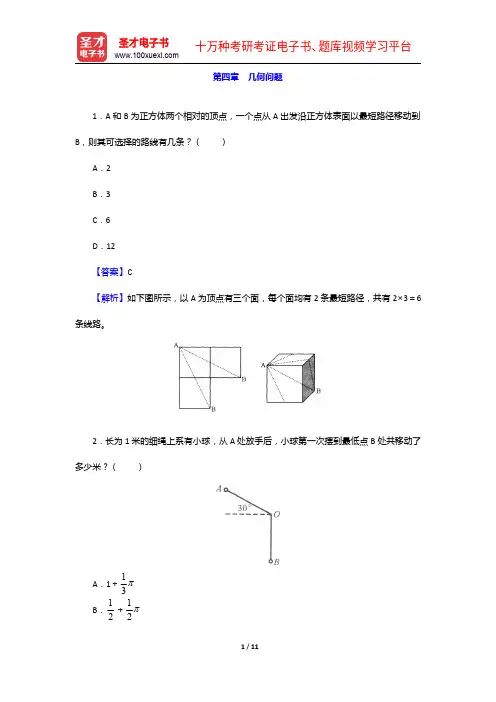
第四章几何问题1．A 和B 为正方体两个相对的顶点，一个点从A 出发沿正方体表面以最短路径移动到B ，则其可选择的路线有几条？（）A ．2B ．3C ．6D ．12【答案】C【解析】如下图所示，以A 为顶点有三个面，每个面均有2条最短路径，共有2×3＝6条线路。

2．长为1米的细绳上系有小球，从A 处放手后，小球第一次摆到最低点B 处共移动了多少米？（）A ．1＋13πB ．12＋12πC ．3πD ．1＋23π【答案】A【解析】如下图所示，C 点和A 点关于中间的虚线对称，小球从A 点到C 点做自由落体运动，从C 点到B 点做半径为1米的圆周运动。

故小球移动的距离为12×1×2＋16×2π＝1＋13π米。

3．一条路上依次有A 、B 、C 三个站点，加油站M 恰好位于AC 的中点，加油站N 恰好位于BC 的中点。

若想知道M 和N 两个加油站之间的距离，只需要知道哪两点之间的距离？（）A ．CNB ．BCC ．AMD ．AB【答案】D【解析】M 与N 点都涉及的顶点为C 点，则MN ＝MC －NC ＝2AC －2BC ＝2AC BC -＝2AB ，即只需要知道AB 两点之间的距离。

4．某公司要在长、宽、高分别为50米、40米、30米的长方体建筑物的表面架设专用电路管道连接建筑物内最远两点，预设的最短管道长度介于（）。

A ．70～80米之间B ．60～70米之间C ．90～100米之间D ．80～90米之间【答案】D 【解析】长方体的侧面的一半展开图如下：如图最远的端点是A 、D 点，架设的管道应相交在长方体的棱上，设交点为E ，所求应为AD ＝22AC CD +，AC 有可能是70，80，90，对应的CD 是50，40，30，且AD ＝()22AB BC CD ++2222AB BC CD AB BC +++⨯，AB ，BC ，CD 的平方和是确定的，若使长度最短则需让2AB ×BC 最小，在三个数字当中选较小的两个，30和40，则最短管道长度227050+＝74007480至90米之间。

§13.1算法与程序框图1．算法通常是指按照一定规则解决某一类问题的明确和有限的步骤．2．程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形．通常程序框图由程序框和流程线组成，一个或几个程序框的组合表示算法中的一个步骤；流程线带方向箭头，按照算法步骤的执行顺序将程序框连接起来．3．三种基本逻辑结构(1)顺序结构是由若干个依次执行的步骤组成的，这是任何一个算法都离不开的基本结构．其结构形式为(2)条件结构是指算法的流程根据给定的条件是否成立而选择执行不同的流向的结构形式．其结构形式为(3)循环结构是指从某处开始，按照一定的条件反复执行某些步骤的情况．反复执行的步骤称为循环体．循环结构又分为当型(WHILE型)和直到型(UNTIL型)．其结构形式为4．5.条件语句(1)程序框图中的条件结构与条件语句相对应．(2)条件语句的格式及框图①IF—THEN格式IF条件THEN语句体END IF②IF—THEN—ELSE格式IF条件THEN语句体1ELSE语句体2END IF6．循环语句(1)程序框图中的循环结构与循环语句相对应．(2)循环语句的格式及框图．①UNTIL语句②WHILE语句DO WHILE条件循环体循环体LOOP UNTIL条件WEND1．判断下面结论是否正确(请在括号中打“√”或“×”)(1)算法只能解决一个问题，不能重复使用．(×)(2)程序框图中的图形符号可以由个人来确定． ( × ) (3)输入框只能紧接开始框，输出框只能紧接结束框．( × ) (4)条件结构的出口有两个，但在执行时，只有一个出口是有效的． ( √ ) 2．下列关于“赋值语句”叙述正确的是( )A ．3.6＝x 是赋值语句B ．利用赋值语句可以进行代数式的化简C ．赋值语句中的等号与数学中的等号意义相同D ．赋值语句的作用是先计算出赋值号右边表达式的值，然后把该值赋给赋值号左边的变量，使该变量的值等于表达式的值 答案 D3．计算机执行下面的程序段后，输出的结果是( )a ＝1,b ＝3 a ＝a ＋b,b ＝a －b PRINT a ，b,ENDA ．1,3B ．4,1C ．0,0D ．6,0 答案 B4．如图，是求实数x 的绝对值的算法程序框图，则判断框①中可填________．答案 x >0？(或x ≥0？)解析 由于|x |＝⎩⎪⎨⎪⎧ x ， x ≥0，－x ，x <0或|x |＝⎩⎪⎨⎪⎧x ，x >0，－x ，x ≤0，故根据所给的程序框图，易知可填“x >0？”或“x ≥0？”．5．(2012·福建)阅读如图所示的程序框图，运行相应的程序，输出的s 值等于________．答案－3解析第一次循环：s＝1，k＝1<4，s＝2×1－1＝1，k＝1＋1＝2；第二次循环：k＝2<4，s＝2×1－2＝0，k＝2＋1＝3；第三次循环：k＝3<4，s＝2×0－3＝－3，k＝3＋1＝4；当k＝4时，k<4不成立，循环结束，此时s＝－3.题型一算法的顺序结构例1f(x)＝x2－2x－3.求f(3)、f(－5)、f(5)，并计算f(3)＋f(－5)＋f(5)的值．设计出解决该问题的一个算法，并画出程序框图．思维启迪算法的设计方案并不唯一，同一问题，可以有不同的算法．设计算法时要注意算法的“明确性”、“有限性”．解算法如下：第一步，令x＝3.第二步，把x＝3代入y1＝x2－2x－3.第三步，令x＝－5.第四步，把x＝－5代入y2＝x2－2x－3.第五步，令x＝5.第六步，把x＝5代入y3＝x2－2x－3.第七步，把y1，y2，y3的值代入y＝y1＋y2＋y3.第八步，输出y1，y2，y3，y的值．该算法对应的程序框图如图所示：思维升华给出一个问题，设计算法应注意：(1)认真分析问题，联系解决此问题的一般数学方法；(2)综合考虑此类问题中可能涉及的各种情况；(3)将解决问题的过程划分为若干个步骤；(4)用简练的语言将各个步骤表示出来．输出的a，b，c分别是()A．75,21,32B．21,32,75C．32,21,75D．75,32,21答案 A解析由程序框图中的各个赋值语句可得x＝21，a＝75，c＝32，b＝21，故a，b，c分别是75,21,32.题型二算法的条件结构例2下图中x1，x2，x3为某次考试三个评阅人对同一道题的独立评分，p为该题的最终得分．当x1＝6，x2＝9，p＝8.5时，x3等于()A ．11B ．10C ．8D ．7思维启迪 依据第二个判断框的条件关系，判断是利用x 2＝x 3还是利用x 1＝x 3从而验证p 是否为8.5. 答案 C解析 x 1＝6，x 2＝9，|x 1－x 2|＝3<2不成立，即为“否”，所以再输入x 3；由绝对值的意义(一个点到另一个点的距离)和不等式|x 3－x 1|<|x 3－x 2|知，点x 3到点x 1的距离小于点x 3到x 2的距离，所以当x 3<7.5时，|x 3－x 1|<|x 3－x 2|成立，即为“是”，此时x 2＝x 3，所以p ＝x 1＋x 32，即6＋x 32＝8.5，解得x 3＝11>7.5，不合题意；当x 3>7.5时，|x 3－x 1|<|x 3－x 2|不成立，即为“否”，此时x 1＝x 3，所以p ＝x 3＋x 22，即x 3＋92＝8.5，解得x 3＝8>7.5，符合题意，故选C.思维升华 (1)条件结构中条件的判断关键是明确条件结构的功能，然后根据“是”的分支成立的条件进行判断；(2)对条件结构，无论判断框中的条件是否成立，都只能执行两个分支中的一个，不能同时执行两个分支．如图，若依次输入的x 分别为5π6、π6，相应输出的y 分别为y 1、y 2，则y 1、y 2的大小关系是( )A ．y 1＝y 2B ．y 1>y 2C ．y 1<y 2D ．无法确定答案 C解析 由程序框图可知，当输入的x 为5π6时，sin 5π6>cos 5π6成立，所以输出的y 1＝sin 5π6＝12；当输入的x 为π6时，sin π6>cos π6不成立，所以输出的y 2＝cos π6＝32，所以y 1<y 2.题型三 算法的循环结构例3 (2013·天津)阅读如图所示的程序框图，运行相应的程序，则输出n 的值为( )A ．7B ．6C ．5D ．4思维启迪 观察程序框图，明确是何种循环结构，明确循环体与循环变量是解决问题的关键． 答案 D解析 第一次：S ＝0＋(－1)1×1＝－1<2，n ＝1＋1＝2， 第二次：S ＝－1＋(－1)2×2＝1<2，n ＝2＋1＝3， 第三次：S ＝1＋(－1)3×3＝－2<2，n ＝3＋1＝4，第四次：S ＝－2＋(－1)4×4＝2，满足S ≥2， 故输出的n 值为4，选D.思维升华 利用循环结构表示算法应注意的问题 第一：注意是利用当型循环结构，还是直到型循环结构．直到型循环结构：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环．当型循环结构：在每次执行循环体前，对条件进行判断，当条件满足时，执行循环体，否则终止循环．第二：注意选择准确的表示累计的变量．第三：注意在哪一步开始循环，满足什么条件不再执行循环体．(2013·辽宁)执行如图所示的程序框图，若输入n ＝8，则输出S 等于( )A.49B.67C.89D.1011答案 A解析 执行第一次循环后，S ＝13，i ＝4；执行第二次循环后，S ＝25，i ＝6；执行第三次循环后，S ＝37，i ＝8；执行第四次循环后，S ＝49，i ＝10；此时i ＝10＞8，输出S ＝49.题型四 基本算法语句例4 阅读下面两个算法语句：执行图1中语句的结果是输出________；执行图2中语句的结果是输出________．思维启迪理解算法语句中两种循环语句的结构和作用是解题的关键．答案i＝4i＝2解析执行语句1，得到(i，i·(i＋1))结果依次为(1,2)，(2,6)，(3,12)，(4,20)，故输出i＝4. 执行语句2的情况如下：i＝1，i＝i＋1＝2，i·(i＋1)＝6<20(是)，结束循环，输出i＝2.思维升华解决算法语句有三个步骤：首先通读全部语句，把它翻译成数学问题；其次领悟该语句的功能；最后根据语句的功能运行程序，解决问题．设计一个计算1×3×5×7×9×11×13的算法．图中给出了程序的一部分，则在横线上不能填入的数是()A．13 B．13.5 C．14 D．14.5答案 A解析当填i<13时，i值顺次执行的结果是5,7,9,11，当执行到i＝11时，下次就是i＝13，这时要结束循环，因此计算的结果是1×3×5×7×9×11，故不能填13，但填的数字只要超过13且不超过15均可保证最后一次循环时，得到的计算结果是1×3×5×7×9×11×13.循环规律与程序中的逻辑顺序不明确致误典例：(5分)为了求满足1＋2＋3＋…＋n<2 013的最大的自然数n，程序框图如图所示，则输出框中应填输出()A．i－2 B．i－1 C．i D．i＋1易错分析本题易出现的错误主要有两个方面：(1)循环规律不明确，导致S与i的关系错误．(2)程序框图中S＝S＋i与i＝i＋1的逻辑顺序不明确，导致错误．解析依次执行程序框图：S＝0＋1，i＝2；S＝0＋1＋2，i＝3；S＝0＋1＋2＋3，i＝4；……由此可得S＝1＋2＋3＋…＋n时，i＝n＋1；经检验知当S＝1＋2＋3＋…＋62＝1 953时，i＝63，满足条件进入循环；S＝1＋2＋3＋…＋62＋63＝2 016时，i＝64，不满足条件，退出循环．所以应该输出62，即i－2.故选A.答案 A温馨提醒(1)解决程序框图问题要注意的三个常用变量：①计数变量：用来记录某个事件发生的次数，如i＝i＋1.②累加变量：用来计算数据之和，如S＝S＋i.③累乘变量：用来计算数据之积，如p＝p×i.(2)循环体规律的探求通常由开始一步一步运行，根据判断条件，那么几步后就会输出结果或会呈现出规律，再根据规律计算出结果.方法与技巧1．在设计一个算法的过程中要牢记它的五个特征：概括性、逻辑性、有穷性、不唯一性、普遍性．2．在画程序框图时首先要进行结构的选择．若所要解决的问题不需要分情况讨论，只用顺序结构就能解决；若所要解决的问题要分若干种情况讨论时，就必须引入条件结构；若所要解决的问题要进行许多重复的步骤，且这些步骤之间又有相同的规律时，就必须引入变量，应用循环结构．3．程序框图的条件结构和循环结构分别对应算法语句的条件语句和循环语句，两种语句的阅读理解是复习重点．失误与防范1．注意起止框与处理框、判断框与循环框的不同．2．注意条件结构与循环结构的联系：对于循环结构有重复性，条件结构具有选择性没有重复性，并且循环结构中必定包含一个条件结构，用于确定何时终止循环体．3．循环语句有“直到型”与“当型”两种，要区别两者的异同，主要解决遇到需要反复执行的任务时，用循环语句来编写程序．4．关于赋值语句，有以下几点需要注意：(1)赋值号左边只能是变量名字，而不是表达式，例如3＝m是错误的．(2)赋值号左右不能对换，赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量，例如Y＝x，表示用x的值替代变量Y的原先的取值，不能改写为x＝Y.因为后者表示用Y 的值替代变量x的值．(3)在一个赋值语句中只能给一个变量赋值，不能出现多个“＝”.A组专项基础训练一、选择题1．已知一个算法：(1)m＝a.(2)如果b<m，则m＝b，输出m；否则执行第3步．(3)如果c<m，则m＝c，输出m.如果a＝3，b＝6，c＝2，那么执行这个算法的结果是()A．3 B．6 C．2 D．m答案 C解析 当a ＝3，b ＝6，c ＝2时，依据算法设计，执行后，m ＝a ＝3<b ＝6，c ＝2<a ＝3＝m ， ∴c ＝2＝m ，即输出m 的值为2，故选C.2．(2013·陕西)根据下列算法语句，当输入x 为60时，输出y 的值为 ( )输入xIf x ≤50 Then y ＝0.5]y ＝25＋0.6]A ．25B ．30C ．31D ．61答案 C解析 由题意，得y ＝⎩⎪⎨⎪⎧0.5x ，x ≤50，25＋0.6(x －50)，x >50.当x ＝60时，y ＝25＋0.6×(60－50)＝31. ∴输出y 的值为31.3．(2013·安徽)如图所示，程序框图(算法流程图)的输出结果为 ( )A.34B.16C.1112 D.2524答案 C解析 赋值S ＝0，n ＝2 进入循环体：检验n ＝2<8，S ＝0＋12＝12，n ＝2＋2＝4； 检验n <8， S ＝12＋14＝34， n ＝4＋2＝6； 检验n <8， S ＝34＋16＝1112， n ＝6＋2＝8，检验n ＝8，脱离循环体，输出S ＝1112.4．(2013·重庆)执行如图所示的程序框图，则输出的k 的值是( )A ．3B ．4C ．5D ．6答案 C解析 由题意，得k ＝1时，s ＝1；k ＝2时，s ＝1＋1＝2；k ＝3时，s ＝2＋4＝6；k ＝4时，s ＝6＋9＝15；k ＝5时，s ＝15＋16＝31>15，此时输出的k 值为5. 5．(2012·天津)阅读如图所示的程序框图，运行相应的程序，当输入x 的值为－25时，输出x 的值为( ) A ．－1 B ．1 C ．3D ．9答案 C解析 当x ＝－25时，|x |>1，所以x ＝25－1＝4>1， x ＝4－1＝1>1不成立，所以输出x ＝2×1＋1＝3. 二、填空题6．已知函数y ＝⎩⎪⎨⎪⎧log 2x ，x ≥2，2－x ，x <2.图中表示的是给定x 的值，求其对应的函数值y 的程序框图．①处应填写________；②处应填写________．答案 x <2？ y ＝log 2x解析 框图中的①就是分段函数解析式两种形式的判断条件，故填写x <2？，②就是函数的另一段表达式y ＝log 2x .7．运行如下所示的程序，当输入a ，b 分别为2,3时，最后输出的m 的值为________．答案 3解析 ∵a ＝2，b ＝3，∴a <b ，应把b 值赋给m ，∴m 的值为3.8．(2013·浙江)若某程序框图如图所示，则该程序运行后输出的值等于________．答案 95解析 当k ＝5时，输出S .此时，S ＝1＋11×2＋12×3＋13×4＋14×5＝1＋1－12＋12－13＋13－14＋14－15＝2－15＝95.9．给出一个如图所示的程序框图，若要使输入的x 值与输出的y 值相等，则这样的x 值是________．答案 0,1,3解析 根据题意，本程序框图表示分段函数：y ＝⎩⎪⎨⎪⎧x 2，x ≤2，2x －3，2<x ≤5，1x ，x >5，由于输入的x 值与输出的y 值相等， 由x 2＝x 解得x ＝0或x ＝1，都满足x ≤2； 由x ＝2x －3解得x ＝3，也满足2<x ≤5； 由1x ＝x 解得x ＝±1，不在x >5内，舍去． 可见满足条件的x 共三个：0,1,3.10．执行下边的程序框图，若p ＝0.8，则输出的n ＝________.答案 4解析 第一次，S ＝12，n ＝2；第二次，S ＝12＋14，n ＝3；第三次，S ＝12＋14＋18，n ＝4.因为S ＝12＋14＋18>0.8，所以输出的n ＝4.B 组 专项能力提升1．(2013·课标全国Ⅱ)执行右面的程序框图，如果输入的N ＝4，那么输出的 S 等于( )A ．1＋12＋13＋14B ．1＋12＋13×2＋14×3×2C ．1＋12＋13＋14＋15D ．1＋12＋13×2＋14×3×2＋15×4×3×2答案 B解析 第一次循环，T ＝1，S ＝1，k ＝2；第二次循环，T ＝12，S ＝1＋12，k ＝3；第三次循环，T ＝12×3，S ＝1＋12＋12×3，k ＝4，第四次循环，T ＝12×3×4，S ＝1＋12＋12×3＋12×3×4，k ＝5，此时满足条件输出S ＝1＋12＋12×3＋12×3×4，选B. 2．如图所示的程序框图中，令a ＝tan θ，b ＝sin θ，c ＝cos θ，若在集合{θ|－π4<θ<3π4，θ≠0，π4，π2}中，给θ取一个值，输出的结果是sin θ，则θ的值所在的范围是 ( )A ．(－π4，0)B ．(0，π4)C ．(π4，π2)D ．(π2，3π4)答案 D解析 依题意该程序为求解a ＝tan θ，b ＝sin θ，c ＝cos θ的最大值， ⎩⎪⎨⎪⎧sin θ>cos θ，sin θ>tan θ，所以θ的值所在范围是(π2，3π4)．3．如图是求12＋22＋32＋…＋1002的值的程序框图，则正整数n ＝________.答案 100解析 第一次判断执行后，i ＝2，s ＝12；第二次判断执行后，i ＝3，s ＝12＋22，而题目要求计算12＋22＋…＋1002，故n ＝100.4．执行如图所示的程序框图，则输出的S 的值是________．答案 300解析 k ＝1<20成立，执行第一次循环体，S ＝0＋3×1，k ＝1＋2＝3；k ＝3<20成立，执行第二次循环体，S ＝3×1＋3×3，k ＝3＋2＝5；k ＝5<20成立，执行第三次循环体，S ＝3×1＋3×3＋3×5，k ＝5＋2＝7；…；k ＝19<20成立，执行第十次循环体，S ＝3×1＋3×3＋…＋3×19，k ＝19＋2＝21；k ＝21<20不成立，跳出循环体，输出的S ＝3×1＋3×3＋…＋3×19＝10×(3＋3×19)2＝300.5. 如图所示，已知底角为45°的等腰梯形ABCD ，底边BC 长为7 cm ，腰长为22cm ，当一条垂直于底边BC (垂足为F )的直线l 从B 点 开始由左至右移动(与梯形ABCD 有公共点)时，直线l 把梯形分成 两部分，令BF ＝x (0≤x ≤7)，左边部分的面积为y ，求y 与x 之间 的函数关系式，画出程序框图，并写出程序．解 过点A ，D 分别作AG ⊥BC ，DH ⊥BC ，垂足分别是G ，H .∵四边形ABCD 是等腰梯形， 底角是45°，AB ＝2 2 cm ， ∴BG ＝AG ＝DH ＝HC ＝2 cm.又BC ＝7 cm ，∴AD ＝GH ＝3 cm ，所以y ＝⎩⎪⎨⎪⎧12x 2(0≤x ≤2)2x －2 (2<x ≤5)－12(x －7)2＋10 (5<x ≤7).程序框图如下：程序：INPUT “x ＝”；x IF x>＝0 AND x<＝2 THEN y ＝0.5 *x^2 ELSEIF x<＝5 THEN y ＝2]。

目录教学计划 (2)第1章金融体系 (3)1.1现代金融制度 (3)1.2西方国家金融体系 (3)1.3我国金融体系 (3)第2章货币与货币制度 (5)2.1货币的功能 (5)2.2支付制度的演进 (5)2.3货币制度的沿革 (6)第3章信用 (7)3.1信用的主要形式 (7)3.2金融工具的性质 (7)3.3金融工具的种类 (8)第4章利息与利率 (9)4.1利息与利率 (9)4.3利率决定理论 (10)第5章金融市场（一） (11)5.1市场参与者 (11)5.2市场组织与结构 (12)5.3货币市场 (12)第6章金融市场（二） (13)6.1股权市场 (13)6.2长期债券市场 (14)6.3金融衍生市场 (15)第7章................................................................................................. 商业银行（一） (15)7.1商业银行制度 (16)7.2商业银行资产负债业务 (16)7.3商业银行中间业务 (16)第8章商业银行（二） (17)8.1商业银行经营原则与管理方法 (18)8.2银行业监管制度 (18)8.3商业银行金融创新 (18)第9章中央银行 (19)9.1中央银行制度 (20)9.2中央银行职能 (20)9.3中央银行的独立性 (21)第10章货币需求 (22)10.1货币需求概述 (22)10.2宏观货币需求理论 (23)10.3微观货币需求理论 (23)第11章货币供给 (24)11.1货币的范围与层次 (25)11.2货币供给行为 (25)11.3货币供给理论 (25)第12章通货膨胀 (27)12.1货币供求的均衡与非均衡 (27)12.2通货膨胀的类型 (27)12.3通货膨胀的经济、社会效应 (28)第13章货币政策 (29)13.1货币政策目标 (29)13.2货币政策工具 (30)13.3货币政策中介目标与传导机制 (30)教学计划第1章金融体系【本章教学目的与要求】通过本章的学习，要求学生对现代金融制度有框架式的了解，熟悉和掌握西方国家和我国金融机构体系的构成和特点。

[经济与管理]理论经济文章编号:1003-6636(2010)01-0001-06;中图分类号:F014.3;文献标识码:A论市场失灵的判别标准伍世安,杨青龙(江西财经大学经济学院,江西南昌330013)摘要:判别市场失灵既有具体标准,也有抽象标准,从实质上说二者是统一的。

具体标准可分为绝对标准(帕累托效率)和相对标准(交易费用),而抽象标准则指个体理性与集体理性的相容。

关键词:市场失灵;帕累托效率;交易费用;个体理性;集体理性O n the C r iter i on ofM ar ket F a il ur eWU Sh i2an,YANG Q i ng2l ong(School of E cono m i cs,J i angxiUn i versity of F i nance and Eco no m ics,Nanchang,Jiangxi330013,China)A bstr ac t:There are both concrete cr iterio n and abstract criter i on of m arket fa ilure.In essence,t hey coi nc i de.Co ncrete criter i oncan be e ithe r absol ute(Pa re t o effi c i ency)or re lati ve(transacti on cost),and abstract cr iter i on refe rs to co mpati b ilit y bet ween i nd i vidual rati ona lity and collecti ve ratio na lity.K ey w ord s:ma rket f a il ure;P areto effi c iency;transactio n cost;ind i vi dua l rati onalit y;collecti ve ra ti ona li ty/市场失灵0(mar ket f a ilure)是经济学中的一个关键词,市场失灵理论是衔接新古典微观经济学与凯恩斯宏观经济学的一根纽带,市场失灵与政府干预之间的关系被经济学家曼昆(N.Gregory Mank i w, 2001)[1]喻为/经济学十大原理0之一。