五邑大学数学分析试题

五邑大学硕士试题及答案一、单项选择题（每题2分，共20分）1. 五邑大学位于哪个省份？A. 广东省B. 广西省C. 湖南省D. 湖北省答案：A2. 五邑大学的校训是什么？A. 厚德博学B. 求实创新C. 明德至善D. 笃学力行答案：B3. 五邑大学成立于哪一年？A. 1985年B. 1995年C. 2005年D. 2015年答案：A4. 五邑大学的主要学科领域包括以下哪项？A. 工程学B. 法学C. 医学D. 所有以上选项5. 五邑大学的学生总数大约是多少？A. 5000人B. 10000人C. 15000人D. 20000人答案：C6. 五邑大学的图书馆藏书量是多少？A. 50万册B. 100万册C. 150万册D. 200万册答案：B7. 五邑大学是否设有研究生院？A. 是B. 否答案：A8. 五邑大学的校徽颜色是什么？A. 蓝色和白色B. 红色和黄色C. 绿色和金色D. 黑色和银色答案：A9. 五邑大学是否提供海外交流项目？A. 是B. 否10. 五邑大学的学生社团数量大约是多少？A. 20个B. 50个C. 80个D. 100个答案：C二、多项选择题（每题3分，共15分）1. 五邑大学的以下哪些学科是优势学科？A. 工程学B. 经济学C. 管理学D. 法学答案：A, B, C2. 五邑大学提供的学位类型包括：A. 学士B. 硕士C. 博士D. 博士后答案：A, B, C3. 五邑大学的学生可以参加哪些类型的活动？A. 学术讲座B. 文化节C. 体育竞赛D. 社会实践答案：A, B, C, D4. 五邑大学的校园设施包括：A. 图书馆B. 实验室C. 体育馆D. 学生宿舍答案：A, B, C, D5. 五邑大学的学生可以获得哪些类型的奖学金？A. 学术奖学金B. 体育奖学金C. 艺术奖学金D. 社会服务奖学金答案：A, B, C, D三、简答题（每题5分，共20分）1. 请简述五邑大学的办学理念。

命题人：金旺春审批人: 试卷分类（A卷或B卷） A五邑大学试卷学期： 2012至 2013学年度第一学期课程：数据结构与算法专业：班级：姓名：学号：答案的序号填在题干的括号内。

每小题2分，共20分)1. 二叉树的先序序列和后序序列正好相同，则该二叉树一定是( )的二叉树。

A. 任一结点无右孩子B.高度等于其结点数C.任一结点无左孩子D.空或只有一个结点2.一个栈的输入序列为1 2 3 4 5，则下列序列中不可能是栈的输出序列的是( )A. 2 3 4 1 5B. 2 3 1 4 5C. 5 4 1 3 2D. 1 5 4 3 23.设循环队列中数组的下标范围是0～n-1，其头尾指针分别为f和r，则其元素个数为( )A. r-fB. r-f+1C. (r-f) mod n +1D. (r-f+n) mod n4.若某链表最常用的操作是在最后一个结点之后插入一个结点和删除第一个结点，则采用( )存储方式最节省时间。

A.单链表B.单循环链表C. 双链表D.带头结点的双循环链表5.在有n个结点的二叉链表中，非空的链域的个数为( )A. n-1B. 2n-1C. n+1D. 2n+16.对有18个元素的有序表作二分查找，则查找A［3］的比较序列的下标依次为( )A. 1，2，3B. 9，5，2，3C. 9，5，3D. 9，4，2，37. 基于邻接表的DFS算法的时间复杂度为( )A. O(n)B. O(n3)C. O(n2)D. O(n+e)8. 队列操作的原则是( )A.先进先出B.后进先出C.只能进行插入D.只能进行删除9.有64个结点的完全二叉树的深度为( )(根的层次为1)。

A. 8B. 7C. 6D. 5A ．栈 B. 队列 C. 完全二叉树 D. 堆判断题(判断下列各题，正确的在题后括号内打“√”，错的打“×”。

每小题1分，共10分)1.给出不同的输入序列建造二叉排序树，一定得到不同的二叉排序树。

五邑大学 试 卷学期： 2014 至 2015 学年度 第 1 学期 课程：高级运筹学 任课教师（命题人）： 使用班级： 经管研2014 姓名： 学号： 2111401002一、构建下述问题的线性规划数学模型并用系统软件求解（10分）生产需要2.9米、2.1米和1.5米的元钢各100根，已知原材料的长度是7.4米，问应如何下料，才能使所消耗的原材料最省。

说明利用的是什么软件，求解的结果和重要的截图。

解：分析可得，每一根原材料的下料方案有如下几种：87654321x x x x x x x x 、、、、、、、根，所需要的原材料的总根数为z 根.数学模型如下：目标函数为：87654321min x x x x x x x x Z +++++++=10024321≥+++x x x x10023276532≥++++x x x x x 1004323876431≥+++++x x x x x x087654321≥x x x x x x x x 、、、、、、、且为整数这是一个线性规划问题，我用的软件lingo 来解这道题，以下就是我用软件解这道题的重要步骤：1、打开lingo 软件2、输入上述线性规划模型3、运行软件，结果如下由软件的运行结果可知，最优解如下，耗费原材料90根，其中按方案一下料的原材料为40根，按方案二下料的原材料为20根，按方案六下料的原材料为30根。

二、用图解法求解下述线性规划问题（5分）2153max x x Z +=123221≤+x x204521≤+x x321≥+x x0,021≥≥x x解：由题意可得，以21x x 、为坐标轴建立直角坐标系（1）根据约束条件画出与约束条件相应方程的直线，由这些直线共同确定出一个 区域，即可行解的区域可行区域如下图所示：为纵轴为横轴，21x x其中，01232:121=-+x x Y Y2：0204521=-+x x Y3：0321=-+x x其中阴影部分的每一个点都是这个线性规划问题的解。

五邑大学考试试题一、选择题（每题2分，共20分）1. 五邑大学位于中国的哪个省份？A. 广东省B. 江苏省C. 浙江省D. 四川省2. 下列哪项不是五邑大学的校训？A. 求实B. 创新C. 团结D. 勤奋3. 五邑大学成立于哪一年？A. 1985年B. 1990年C. 1995年D. 2000年4. 五邑大学的主要教学语言是什么？A. 英语B. 普通话C. 粤语D. 闽南语5. 以下哪个学院不属于五邑大学？A. 经济管理学院B. 法学院C. 医学院D. 信息工程学院6. 五邑大学的校庆日是哪一天？A. 5月8日B. 10月1日C. 11月11日D. 12月20日7. 五邑大学的学生宿舍通常几人一间？A. 2人B. 4人C. 6人D. 8人8. 五邑大学图书馆的开放时间是？A. 8:00 - 22:00B. 9:00 - 21:00C. 8:30 - 21:30D. 9:30 - 20:309. 五邑大学的运动场馆包括以下哪些设施？A. 足球场B. 篮球场C. 游泳池D. 所有以上10. 下列哪项不是五邑大学提供的学生服务？A. 心理咨询B. 法律咨询C. 医疗服务D. 职业规划二、填空题（每题2分，共20分）11. 五邑大学的校徽由_______、_______和_______三部分组成。

12. 五邑大学的学生社团联合会简称为_______。

13. 五邑大学的教学理念是“以学生为中心，以_______为导向”。

14. 五邑大学每年的_______是学生展示自己科研成果的重要活动。

15. 五邑大学校园内的主要道路以_______命名，以纪念学校的创办者。

16. 五邑大学的学生食堂提供_______、_______和_______等多种餐饮服务。

17. 五邑大学的学生宿舍区被称为_______，是学生日常生活的主要区域。

18. 五邑大学的学生可以在_______和_______两个校区之间自由选择上课。

五邑大学 答卷纸学期： 2007 至 2008 学年度 第 1 学期 课程： 数据库原理 专业： 信息学院各专业 班级： 姓名： 学号：一、填空题（10分，每题1分）1． HA VING 2. DISTINCT 3. 需求分析 4. 操作类型5． 存取 6. REVOKE 7. 日志文件 8. 参照9． 共享锁 10. 删除异常二、 判断题 （在括号内正确的打√，错误的打╳，每题1分 共10分）。

选择题（30分，每题1分）四、关系代数及SQL语句（每小题2分，共24分）1答案及评分标准：1、（1）π书号,书名(σ作者=‘李东’(书))1分 1分 （2）π读者号,姓名(σ部门＝‘计算机系’∧性别=‘女’(读者))1分 1分（3）π书名,姓名(π读者号,书名(σ书号=‘J58’(借书) ∞书)∞ 读者)1分 （无π读者号,书名不扣分）1分（4）π读者号(读者)－π读者号(π书号(σ书名=‘计算机网络’(书)) ∞借书)1分 1分 （无π书号不扣分）2、（1）INSERT INTO 书(书号，书名，作者，出版社) (1分)V ALUES （‘J101’，‘数据库理论’，‘王铭’，‘科学出版社’）(1分)（2）SELECT 读者号，借出日期，应还日期 FROM 借书，书 (1分)WHERE 书. 书号=借书. 书号 AND 书.书名=‘数据库理论’(1分)（3）SELECT 借书.书号，书名，作者，COUNT （借书. 书号）(COUNT 部分 1分)FROM 借书，书WHERE 借书.书号=书.书号 GROUP BY 借书.书号 (GROUP BY 部分1分)（4）SELECT 书名，借书.读者号，姓名FROM 读者，书，借书 (1分)WHERE 书.书号=借书.书号 AND 读者.读者号=借书.读者号AND 书号=‘J18’ (1分)fppWHERE 部门=‘计算机系’ (1分)（6）GRANT SELECT, DELETE (1分)ON 借书 TO USER1 (1分，表前加TABLE 不扣分)（7） SELECT * FROM 书WHERE 书名 LIKE ‘数据库%’ (LIKE 1分，‘数据库%’1分)（8）CREATE VIEW RL （读者号，姓名，书号，书名，借出日期，应还日期）(1分)AS SELECT 借书.读者号，姓名，借书.书号，书名，借出日期，应还日期 FROM 读者，书，借书WHERE 书. 书号=借书. 书号 AND 读者.读者号=借书. 读者号 (1分)五、 规范化理论（10分）参考答案：（1）确定关系R 的码(1分)关系模式的码为：（任课教师，课程编号）……………………1分(2)写出关系R 的函数依赖(3分)（任课教师，课程编号） 学生人数 ………………………1分课程编号→课程名称 ，（任课教师，课程编号）→课程名称………………1分课程编号→教材作者，（任课教师，课程编号）→ 教材作者………………1分(3) 判断关系R 最高为第几范式？为什么？（2分）答：该关系模式的各属性都满足原子性要求，故满足1NF ，R 最高为第一范式……………1分；因为关系模式中存在非主属性对码的部分函数依赖关系，………………1分（4）将R 分解成3NF 的关系模式为：(4分) R1(任课教师，课程编号，学生人数)……………………………1分主码：（任课教师，课程编号），外码：课程编号………………1分 R2(课程编号，课程名称，教材作者) …………………………….…1分主码：课程编号 ………………………………………………1分六、数据库设计（共16’）答：1. 4个实体类型图4’2．E-R 图 5’2’3’3.如果仓库与商品之间是1：n 的联系，则按如下方式转换：◆ 商品(商品编号，商品名，类别，单价，仓库编号，库存量) 2’主码：商品编号 外码：仓库编号 { 或✧ 商品(商品编号，商品名，类别，单价) 1’ 主码：商品编号 外码：无 ✧ 存放(商品编号，仓库编号，库存量) 1’ 主码：商品编号 外码：仓库编号 }如果仓库与商品之间是m ：n 的联系，则按如下方式转换： ◆ 商品(商品编号，商品名，类别，单价) 1’ 主码：商品编号 外码：无 ◆ 存放(商品编号，仓库编号，库存量) 1’主码：商品编号+仓库编号 外码：商品编号，仓库编号◆仓库(仓库编号，地点，面积) 1’主码：仓库编号外码：无◆顾客(顾客编号，顾客名，地址，电话，账号) 1’主码：顾客编号外码：无◆营业员(营业员号，姓名，性别，销售额，销售指标) 1’主码：营业员号外码：无◆销售(商品编号，顾客编号，营业员号，销售日期，数量) 2’主码：商品编号+顾客编号+营业员号+日期外码：商品编号，顾客编号，营业员号。

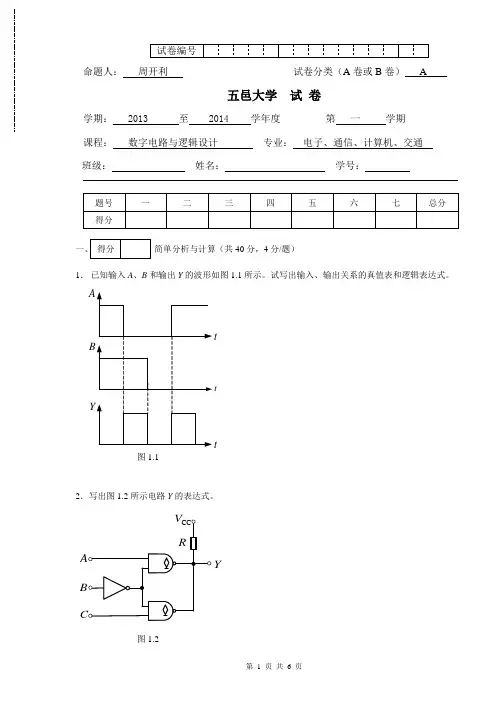
命题人：徐秀平 审批人： 试卷分类（A 卷或B 卷） A五邑大学 试 卷学期： 2008 至 2009 学年度 第 一 学期 课程： 数字电路与逻辑设计 专业： 电子、计算机、交通 班级：姓名： 学号：一、（包含8个小题，共38分）4分）CD D A BD B A Y +++=利用卡诺图化简下面逻辑函数，要求画出卡诺图，求得最简与或式。

（6分） ∑∑+=），），，，，，，，，，138(1514109763210(d m Y.3电路如图所示，①试写出输出端逻辑式；2，已知输入信号的波形，请对应画出输出端的波形。

（4分）A B Y BA Y电路如图所示，其中所有的门均为TTL 门。

若已知各门的参数为I OH =，I OL =14mA ，I IH =，I IL =，试求能带多少个同类门？（4分）电路如图所示，请写出输出Q 的特性方程，并画出对应时钟脉冲CLK 的输出Q 的波形（4分）1. 6电路如图所示，①说明它的容量是多少？②写出各片的地址范围（十六进制表示）。

（6分）A DR'TTL NtR 'ACB555定时器接成的电路如图所示，若V CC =12V ，①试问CB555接成的是什么电路？②若输入电压v I 波形如图所示，试画出输出电压v 0的波形。

（6分）如图所示电路为4位倒T 型电阻网络D/A 转换器。

已知R=10K Ω，V REF =12V 。

当某位数字量d i =1时，开关接S i 接运算放大器的反相输入端，；当d i =0时，开关接S i 接地。

试求：①输出模拟电压v o 的范围；②求d 3d 2d 1d 0=1011时，对应的输出的模拟电压v o 值。

（4分）二、分析题（包含三道题，共32分）由3线－8线译码器74HC138构成的逻辑电路如图所示，分析电路的逻辑功能，要求写出输出端逻辑式和真值表，说明电路有什么作用。

（10分）S 11X 10X 1174HC 的功能表32S S '+'i Y 'i m '组合的最小项为012A A A i mv分析如图所示时序逻辑电路的功能，要求写出电路的驱动方程、状态方程、输出方程，画出状态转换图，说明是什么电路，并检查电路能否自启动。

命题人： 审核人： 试卷分类（A 卷或B 卷） A五邑大学 试 卷学期： 2011 至 2012 学年度 第 1 学期 课程：离散数学课程代号：使用班级： 姓名： 学号：（每小题3分共12分）（1）将下面的命题翻译成命题公式。

1． 如果天不下雨，我就骑自行车上班。

2．不犯我，我不犯人；人若犯我，我必犯人。

（2）将下列命题翻译成谓词公式。

1． 所有的人都要呼吸。

2． 除非李联不怕吃苦，否则她不会取得这样好的成绩。

计算题（每题4分共12分）（1） 求公式)())()((a R x Q P x ∨→∀的真值，其中论域为{-2，3，6}，12:>P ；3:)(≤x x Q ；6:)(≥x x R ；5=a 。

（2） 设集合A ={a,b,c,d,e}上有一各划分S={{a,b},{c},{d,e}}，试由S 确定A 的一个等价关系R 。

三、 计算题（每题6分共30分）（1）给定集合X={0，1，2，3}，R 和S 是X 上的关系，R ={（x,y ）|y=x+1 或 y= x/2 }，S ={ (x,y)|x=y+2} 。

要求1）R,S 是否满足自反、对称、传递性；2）计算关系R S ，。

（2）求集合{1,2,3,…1000}中有多少元素至少能被4，5, 6这三个数中的一个整除。

（3）求公式 R Q P →→)(的主析取范式。

（4）在整数集合I 上，定义二元运算*如： x*y=x+y-5，则1）运算*在I 上可交换和可结合吗？ 2）运算*在I 上有单位元、零元和逆元吗？（5）设A ＝｛1, 2, 3, 4, 5, 8, 10, 20, 40｝，ρ是定义在集合A 上的整除关系， 1）请画出A 中整除关系的哈斯图；2）写出A 的子集B={4，5，8，20}的最大元，最小元，上界，下界。

四、证明题（每题7分共14分） （1）对任意命题公式,,,A B C D ，证明,(),()A B B C C A D D →⌝∨∧⌝⌝⌝∧⇒⌝ （8分） （2）设ρ是整数集合I 上的二元关系， ，试证ρ是I 上的等价关系，并求ρ对应的划分。

信号波形变换为信号分析中的一个难点，通常的方法是对给定的信号波形用反折、时移、尺度变换3种运算按不同的排列顺序依次进行变换。

如反折→时移→尺度变换，反折→尺度变换→时移等6种变换方法。

但不管哪一种变换方法都容易出现错误。

在这里介绍一种简单可靠的方法，很容易得到变换后的波形且准确无误。

具体步聚如下：（1）对给定信号的自变量用t 表示，变换后信号的自变量用x 表示，则本例中的对应自变量为()f t 、(12)f x -。

（2）令括号的变量相等，即12x t -=，解出1(1)2x t =-。

（3）给定不同的t 值，求出相应的x 值，当然最好用已知波形的特殊点所对应的t 值。

如果用拐点处的t 求x ，则x 对应于变换后波形的拐点。

即0t =，12x =；1t =，0x =；2t =，12x =-。

（4）找到各x 值处的信号值。

12x =处的值为对应于0t =处的值，即1()x f x ==0()0t f t ==；0x =处的值为01()()1x t f x f t ====。

同理，122()()1x t f x f t =-===。

各点值对应于图中的'a 、'b 、'c 、'd 各点。

（5）按给定的信号波形变化规律依次连接变换后的信号各x 值的信号值，即得到变换后的波形。

图1（a ）中a b c d →→→对应于图1（b ）中''''a b c d →→→。

（6）需特别注意冲激信号的尺度变换，因为冲激信号的尺度变换对应着冲激强度的变化，即1()()at t aδδ=。

（7）最后令x t =恢复原自变量，如图1（b ）所示。

(f()a图1 波形变换的过程1-2 解： （1）0(2)sin (3)d (2)sin (1)d sin t t t t t δωδωω∞∞--=--=-⎰⎰（2）22200(0)()d ()d 0(0)t e t e t t et t t ττδτδτ---∞∞--⎧ ≥-=-=⎨<⎩⎰⎰ （3）113(3)d (3)d 0j tj t et et t ωωδδ-=-=⎰⎰（4）（1）()()f t y t e =① 1()1()f t y t e =，2()2()f t y t e =，1212()()()()][12()()f t f t f t f t y t y t e e e ++=+≠，所以该系统是非线性系统。

五邑大学第一套线性代数模拟试题解答一、填空题(每小题4分，共24分)1、 若12335544i j a a a a a 是五阶行列式中带正号的一项，则,12i j ==。

令1,2i j ==，(12354)(13524)134τπ+=+=，取正号。

(知识点：行列式的逆序数)2、 若将n 阶行列式D 的每一个元素添上负号得到新行列式D ，则D =(1)n D- 。

即行列式D 的每一行都有一个(-1)的公因子，所以D =(1)n D-。

3、设1101A ⎛⎫=⎪⎝⎭, 则100A =110001⎛⎫ ⎪⎝⎭。

23111112121113,,010*********A A ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫====⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭可得4、设A 为5 阶方阵，5A =，则5A =15n +。

由矩阵的行列式运算法则可知：1555nn A A +==。

答案应该为5的n 次方5、A 为n 阶方阵,TAA E =且=+<E A A 则,0 0 。

由已知条件：211,1T T TAA E AA A A A E A A =⇒====⇒=±⇒=-，而 ：0T TA E A AA A E A A A E A E A E +=+=+=+=-+⇒+=。

6、设三阶方阵2000023A x y ⎛⎫ ⎪= ⎪ ⎪⎝⎭可逆，则,x y 应满足条件32x y ≠。

可逆，则行列式不等于零：2002(32)032023A x y x y x y ==⨯-≠⇒≠。

二、单项选择题(每小题4分，共24分)7、设0333231232221131211≠=M a a a a a aa a a ，则行列式=---------232221333231131211222222222a a a a a a a a a A 。

A ．M 8B ．M 2C ．M 2-D ．M 8-由于()()111213111213111213331323331323321222321222321222331323322222228(1)8222a a a a a a a a a a a a a a a a a a M a a a a a a a a a ------=-=--=---8、设n 阶行列式n D ，则0n D =的必要条件是 D 。

在决定考研的那一刻，我已预料到这一年将是怎样的一年，我做好了全身心地准备和精力来应对这一年枯燥、乏味、重复、单调的机械式生活。

可是虽然如此，我实在是一个有血有肉的人呐，面对诱惑和惰性，甚至几次妥协，妥协之后又陷入对自己深深的自责愧疚当中。

这种情绪反反复复，曾几度崩溃。

所以在此想要跟各位讲，心态方面要调整好，不要像我一样使自己陷入极端的情绪当中，这样无论是对自己正常生活还是考研复习都是非常不利的。

所以我想把这一年的经历写下来，用以告慰我在去年饱受折磨的心脏和躯体。

告诉它们今年我终于拿到了心仪学校的录取通知书，你们的付出和忍耐也终于可以扬眉了。

知道自己成功上岸的那一刻心情是极度开心的，所有心酸泪水，一扫而空，只剩下满心欢喜和对未来的向往。

首先非常想对大家讲的是，大家选择考研的这个决定实在是太正确了。

非常鼓励大家做这个决定，手握通知书，对未来充满着信念的现在的我尤其这样认为。

当然不是说除了考研就没有了别的出路。

只不过个人感觉考研这条路走的比较方便，流程也比较清晰。

没有太大的不稳定性，顶多是考上，考不上的问题。

而考得上考不上这个主观能动性太强了，就是说，自己决定自己的前途。

所以下面便是我这一年来积攒的所有干货，希望可以对大家有一点点小小的帮助。

由于想讲的实在比较多，所以篇幅较长，希望大家可以耐心看完。

文章结尾会附上我自己的学习资料，大家可以自取。

五邑大学数学的初试科目为：(101)思想政治理论(201)英语一(616)数学分析和(818)高等代数参考书目为：1.《数学分析》（上、下册）华东师范大学数学系编(高等教育出版社第四版)2. 《高等代数》北京大学数学力学系编, 高教出版社(第二版).3. 《复变函数论》钟玉泉主编（高等教育出版社第三版）4. 《常微分方程》王高雄等编(高等教育出版社第三版)5.《近世代数》韩士安，林磊著（科学出版社第二版）关于英语复习的建议考研英语复习建议:一定要多做真题，通过对真题的讲解和练习，在不断做题的过程中，对相关知识进行查漏补缺。

共 2 页 第 1 页 0, 0.五邑大学 2023 年攻读硕士学位研究生入学考试自命题科目试卷科目名称： 数学分析 科目代码： 616 提示：①请把答案写在答题纸上，写在试卷上不给分。

②答案应清楚标明题号，字迹应 清晰，卷面要整洁。

③试卷满分 150 分。

一、（每题 10 分，共 30 分）计算下列极限.1. lim tan xsin x x 0x 32. lim (11x )x e x 0 xn 1i 3. lim cos n i 1 n n二、（10 分）设f (x ) x 讨论函数f (x )在x x 处的连续性与可导性.三、（10 分）设 f (x ) 在[a ,b ] 上可导， 且 f (a )(a ,b )，使得 . 证明： 存在 x 2 sin 1 , 0,x 0 f (b ) 0共 2 页 第 2 页 xu yv 1,yu xv 2 sin x 2 y 2dxdy DD {(x ,y ) | 2 x 2 y 2 4 2} .(2x 3y 4z )ds ， L四、（每题 10 分，共 30 分）计算下列不定积分与定积分.1.2.3.x 2五、（10 分）设F (x ) s in (x t )d t ，求F (x ).2x 1六、（10 分）已知方程组 确定u ,v 是关于x ,y 的函数，试求.七 、 （ 10 分 ） 计 算 二 重 积 分 , 其 中八、（10 分）讨论函数列f n(x ) 在[0, )上的一致收敛性.九、（10 分）求曲线积分2f ( ) f ( ) 0. x 2 12x 3 dx0 2e 2x cos x dx1 2x2 dx3v , v x y1 2nxn 2x 2 ,n 1,2,其中L 取自螺旋线：x 2 cos t,y 2 sin t,z3t,(0 t 2 ).十、（10 分）计算三重积分Vx 2y2dxdydz,其中 V 是由曲面所围区域.x 2 y2 z 2和平面z十一、（10 分）设f (x)以2为周期，在[ , ]上有f (x) 里叶级数展开式.x 2，求f (x)的傅1共2 页第3 页。

命题人： 试卷分类（A 卷或B 卷） A五邑大学高等数学竞赛 试 卷专业：班级：姓名： 学号：一、选择题（40分）1. 设n n n y z x ≤≤，且0)(lim =-∞→n n n x y ，则n n z ∞→lim （ C ）(A) 存在且等于零; (B) 存在但不一定等于零； (C) 不一定存在； (D) 一定不存在.2. 设()f x 在x=a 的某个邻域内有定义，则()f x 在x=a 处可导的一个充分条件是 （ D ）（A ）1lim [()()]h h f a f a h →+∞+-存在 （B ）0limh →f(a+2h)-f(a+h)存在h（C ）0lim h →f(a+h)-f(a-h)存在2h （D ）0lim h →f(a)-f(a-h)存在h3. 设ξ为()arctan f x x =在[ 0, ]b上应用拉格朗日中值定理的“中值”，则 22limb b ξ→= （ C ）(A) 1 (B) 12(C)13(D)14.4. 若21(),(0)f x x x'=> ，且(1)2f =，则()f x = （ C ） (A) 2x (B)1ln 22x + (C) (D)5. 设222:D x y a +≤，则DI xy dxdy ==⎰⎰ （B ）(A) 0 (B) 42a (C) 4a(D) 4a π6. 若()f x 的二阶导数存在，且()0,(0)0f x f ''> =，则()()0f x F x x x=<<+∞在上（ A ） (A) 单调增加 (B) 单调减少 (C) 有极小值 (D) 有极大值7. 设L 是曲线2y x =与直线y x =所围成区域的整个边界曲线，(,)f x y 是连续函数，则曲线积分(,)Lf x y ds =⎰（ D ）(A) 11200(,)(,)f x x dx f x x dx +⎰⎰(B) 11200(,)(,f x x dx f x x +⎰⎰(C) 11200(,(,f x x f x x +⎰⎰(D)121[(,(,f x x f x x dx -⎰8.设直线L ：⎩⎨⎧-=---=++3102123z y x z y x ，平面π：224=+-z y x ，则它们的位置关系是 （ C ）.（A ）π//L （B ）L 在π上 （C ）π⊥L （D ）L 与π斜交9. 设函数()()f x g x 与在[0,1]上连续，且()()f x g x ≤，则对任何(0,1)c ∈，有 （ D ）(A) 1122()()ccf t dtg t dt ≥⎰⎰(B)1122()()ccf t dtg t dt ≤⎰⎰(C) 11()()ccf t dtg t dt ≥⎰⎰ (D)11()()ccf t dtg t dt ≤⎰⎰10. 设()f x 为不恒等于零的奇函数，且(0)f '存在，则函数()()f x g x x=（ D ） (A) 在0x =处左极限不存在 （B ）有跳跃间断点0x =(C) 在0x =处右极限不存在 （D ）有可去间断点0x =二、(10分）已知数列120,n n n n U U U U -->=+且，如果数列1nn n U X U +=，且lim n n X A →∞=存在，求A解：11111111n n n n n n n n nU U X U U U U X U -+--====+++， 两边取极限得11A A=+，即210A A +-=，解得A =，所以A =三、（10分）设)(1lim)(2212N n x bxax x x f n n n ∈+++=-∞→，试确定a 、b 的值，使与)(lim 1x f x →)(lim 1x f x -→都存在.解：当||1x <时，221limlim 0n n n n x x -→∞→∞==，故2()f x ax bx =+； 当||1x >时，1()f x x=112111,1,lim ()1,lim (),1(),11,1,1,lim (),lim ()1,1x x x x x f x f x a b a b x f x ax bx x x f x a b f x a b x -+-+→-→-→→⎧<-=-=--=⎪⎪⎪=+-<<⎨⎪⎪>=+=+=⎪⎩所以 0a =，1b =。