当前位置：文档之家 › 《运筹学》第十章 多目标决策模型 第五节 层次分析法与实例

《运筹学》第十章 多目标决策模型 第五节 层次分析法与实例

  • 格式：ppt
  • 大小：2.20 MB
  • 文档页数：48

下载文档原格式

  / 48

合集下载

第五章多目标决策-层次分析法

第五章多目标决策-层次分析法

第13章多目标决策单目标决策问题前三章已经进行了较为详细的探讨。

从合理行为假设引出的效用函数，提供了对这类问题进行合理分析的方法和程序。

但在实际工作中所遇到的的决策分析问题，却常常要考虑多个目标。

这些目标有的相互联系，有的相互制约，有的相互冲突，因而形成一种异常复杂的结构体系，使得决策问题变得非常复杂。

国外一般认为，多目标优化问题最早是在19世纪末由意大利经济学家帕累托（V.Pareto）从政治经济学的角度提出来的，他把许多本质上不可比较的目标，设法变换成一个单一的最优目标来进行求解。

到了20世纪40年代，冯诺曼等人由从对策论的角度提出在彼此有矛盾的多个决策人之间如何进行多目标决策问题。

1950年代初，考普曼（T.C.koopmans）从生产和分配的活动分析中提出多目标最优化问题，并引入了帕累托最优的概念。

1960年代初，菜恩思（F.Charnes）和考柏（J.Cooper）提出了目标规划方法来解决多目标决策问题。

目标规划是线性规划的修正和发展，这一方法不只是对一些目标求得最优，而是尽量使求得的最优解与原定的目标值之间的偏差为最小。

1970年代中期，甘尼（R.L.Keeney）和拉发用比较完整的描述多属性效用理论来求解多目标决策问题。

1970年代末，萨蒂（A.L.Saaty）提出了影响广泛的AHP(the analytical hierarchy process)法，并在1980年代初纂写了有关AHP 法的专著。

自1970年代以来，有关研究和讨论多目标决策的方法也随之出现。

总之，多目标决策问题正愈来愈多的受到人们的重视，尤其是在经济、管理、系统工程、控制论和运筹学等领域中得到了更多的研究和关注。

13.1 基本概念多目标决策和单目标决策的根本区别在于目标的数量。

单目标决策，只要比较各待选方案的期望效用值哪个最大即可，而多目标问题就不如此简单了。

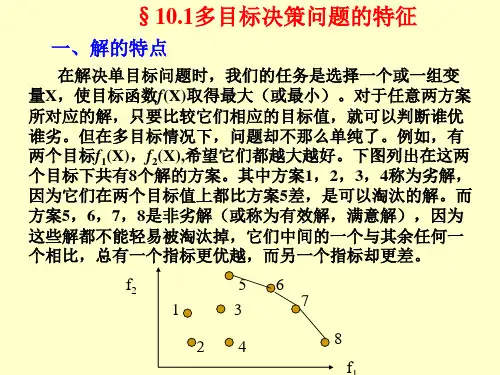
例13.1房屋设计某单位计划建造一栋家属楼，在已经确定地址及总建筑面积的前提下，作出了三个设计方案，现要求根据以下5个目标综合选出最佳的设计方案：1）低造价（每平方米造价不低于500元，不高于700元）；2）抗震性能（抗震能力不低于里氏5级不高于7级）；3）建造时间（越快越好）；4）结构合理（单元划分、生活设施及使用面积比例等）；5）造型美观（评价越高越好）这三个方案的具体评价表如下。

多目标规划模型概述

多目标规划模型概述
在进行下一次迭代时，对应于降低了要求的那些目标fj(j=1,2,…,k)的权系数πi应该设为0。这种迭代继续下去，直到决策者满意为止。
例题：某公司考虑生产两种光电太阳能电池：产品甲和产品乙。这种生产过程会在空气中引起放射性污染。因此，公司经理有两个目标：极大化利润与极小化总的放射性污染。已知在一个生产周期内，每单位甲产品的收益是1元，每单位乙产品的收益是3元。而放射性污染的数量，每单位甲产品是1.5个单位,每单位乙产品是1个单位.由于机器能力(小时)、装配能力（人时）和可用的原材料（单位）的限制，约束条件是
4、步骤法（STEM法） 这是一种交互方法，其求解过程通过分析者与决策者之间的对话逐步进行，故称步骤法。 步骤法的基本思想是，首先需要求出原多目标问题的一组理想解(f1*,f2*,…,fp*)。实际上，这些解fi*(i=1,2,…,p)无法同时达到，但可以当作一组理想的最优值。以理想解作为一个标准，可以估计有效解，然后通过对话，不断修改目标值，并把降低要求的目标作为新的约束条件加入原来的约束条件中去重新计算，直到决策者得到满意的解。 步骤法算法如下：第一步：分别求解以下p个单目标问题的最优解
1、多目标规划问题的模型结构
为决策变量
如对于求极大(max)型，其各种解定义如下：绝对最优解：若对于任意的X，都有F(X*)≥F(X)有效解：若不存在X，使得F(X*)≤ F(X)弱有效解：若不存在X，使得F(X*)<F(X)
2、多目标优选问题的模型结构 可用效用函数来表示。设方案的效用是目标属性的函数：
得到最优解 ，其相应的目标值 即为理想值，此最优解处别的目标所取的值用 表示，即 ，把上述计算结果列入下表
目标有两个:一是利润最大,二是污染最小.该问题的多目标规划模型如下:
解:首先,分别求解两个单目标问题的最优解,由它们得到的目标函数值组成理想解.

层次分析法(AHP)实例介绍 [

层次分析法(AHP)实例介绍 [

层次分析法(AHP)简介Analytical Hierarchy Process层次分析法(AHP)简介⏹美国运筹学家Thomas Saaty⏹70年代末提出⏹定性与定量相结合⏹多目标(Multi-attribute)决策方法AHP Analytical Hierarchy ProcessAHP=Analytical Hierarchy ProcessLean-Six SigmaAHP在我国80年代以后的应用概况•AHP的出现与应用为了测定对象系统的属性，并将这些属性变为客观的定量的计为了测定对象系统的属性并将这些属性变为客观的定量的计值或者主观效用的行为，即对目标系统进行评价，故先后出现了很多不同的评价分析方法，包括专家评价法、经济分析法以及运筹学和其他数学方法。

AHP法属于应用数学方法的一类在实践中筹学和其他数学方法法属于应用数学方法的类在实践中得到广泛应用。

•AHP在我国的研究与应用年代以来，我国的很多领域都先后使用了AHP进行评价与决80年代以来我国的很多领域都先后使用了策。

Lean-Six Sigma一、自然界油资1989石油资源1989环境污染治理方案二、科学技术1988军械系统软科学成果评定1989产业科技水平1989地区科技综合实力1989专科项目的邻选和评价1989科技规划决策1989中科院青年研究基金评审1989农业科技成果评定Lean-Six Sigma三、教育评估教学质1988评估教学质量1989后勤院校教学质量1989大学生综合素质1989毕业生质量1989高校基金分配四、人工制造系统1981987武器系统1987反坦克导弹武器系统方案1989柔性结构系统设计1989择优水利工程开发方案综合评价1989采矿方法可行方案综合评价Lean-Six Sigma五、人和社会系统1987领导能力考评1988专业技术人员评价1989人事管理制度制定1989开放实验室（中科院）1989科协和学会（中国科协）1989工业企业经济效益1989中小企业经济效益1989青海省南州畜牧业发展状况评价Lean-Six SigmaAHP分析基本过程⏹把复杂问题分解成各个组成元素⏹按支配关系将这些元素分组﹑分层（方案层，准则层）按支配关系将这些元素分组分层（方案层准则层）⏹通过两两比较方式判断各层次中诸元素的重要性⏹综合这些判断计算单准则排序和层次总排序⏹确定诸元素在决策中的权重Lean-Six SigmaAHP法(层次分析法)最优化设施布局目标层方案一1.空间利用率方案二方案层•确定各准则的权重2.物流强度3.搬运距离准则层4.扩充弹性1 1/5 1/7 1/3比较矩阵权重0.0571.空间利用率（1）物流强度（） 5 1 1/337 3 1 53 1/3 1/510.2630.55801222.物流强度（5）3.搬运距离（7）4Lean-Six Sigma0.1224.扩充弹性（3）•一致性检验算得CI= 0.04查表得RI=0.90 CR=0.04/0.90=0.044 < 0.1通过一致性检验•水平分值方案比较矩阵0857012501670250 1 61/6 11 1/77 11 1/55 11 1/33 1比较矩阵扩充弹性搬运距离物流强度空间利用率准则方案一水平分值0.8570.1430.1250.8750.1670.8330.2500.750水平分值方案方案二•综合分值0057综合分值扩充弹性搬运距离物流强度空间利用率准则01430875083307500.3610.8570.1250.1670.250方案一0.1220.5580.2630.057权重Lean-Six Sigma0.6390.1430.8750.8330.750方案二方案二最优解读案例目标寻求最佳的方案⏹目标:寻求最佳的方案⏹对象:方案一,方案二⏹主要考虑四个方面的问题✓空间利用率✓物流强度✓搬运距离✓扩充弹性Lean-Six Sigma解读案例布局优选方案目标层空间利物流搬运扩充准则层用率强度距离弹性方案一方案方案二方案层Lean-Six Sigma准则层元素重要性分析空间利物流搬运扩充用率强度距离弹性间利用率空间利用率物流强度搬运距离扩充弹性Lean-Six SigmaLean-Six Sigma判断矩阵构成空间利用率的重要性是物流强度的1/5空间利用率物流强度搬运距离扩充弹性空间利用率 1 1/5 1/7 1/3物流强度 5 1 1/3 37315搬运距离A 7 3 1 53 1/3 1/5 1扩充弹性Lean-Six SigmamLean-Six Sigmaj =1Lean-Six Sigmamw i =Lean-Six Sigma对于本例1 1/5 1/7 1/35 1 1/3 30.2630.057 1.0990.230TAW7 3 1 53 1/3 1/5 10.1220.558=0.4922.355Temp =¼(0.230/0.057+1.099/0.263+2.355/0.558+0.492/0.122)=4.1168=4.1168-4/(4-1)=0.0389CI 4.11684/(41)0.0389查表得RI=0.90 CR=0.04/0.90=0.044 < 0.1通过一致性检验Lean-Six Sigma通过致性检验方案层对于准则的重要性类似的得出•类似的得出2个方案对不同基准的比较矩阵1611/711/51 1/3空间利用率物流强度搬运距离扩充弹性重要方案一 1 61/6 11 1/77 11 1/55 13 1性矩阵方案二0.85701430.12508750.16708330.2500750权方案一0.1430.8750.8330.750重方案二Lean-Six Sigma结果计算•最后一步计算每个方案的优劣最后步计算每个方案的优劣方案一得分=0.057*0.25+0.263*0.167+0.558*0.125+0.122*0.857=0.361方案二得分=0.057*0.75+0.263*0.833+0.558*0.875+0.122*0.143=0.639Lean-Six Sigma案例：物流系统供货商选择的评价与决策⏹研究背景及目的⏹建模及分析过程⏹结论研究背景及目的•货物采购是物流系统一项独立并且重要的功能，供货商的工作情况对物流企业生产率、产品质量及竞争力有很大影工作情况对物流企业生产率产品质量及竞争力有很大影响，因此选择合适的供货商尤为重要。

层次分析法基本原理、实施步骤、应用实例

层次分析法基本原理、实施步骤、应用实例

二、层次分析法的基本原理
层次分析法根据问题的性质和要达到的总目标，将问题分 解为不同的组成因素，并按照因素间的相互关联影响以及 隶属关系将因素按不同层次聚集组合，形成一个多层次的 分析结构模型，从而最终使问题归结为最低层(供决策的 方案、措施等)相对于最高层(总目标)的相对重要权值的确 定或相对优劣次序的排定。
• 最高层：决策的目的、要解决的问题。 • 最低层：决策时的备选方案。 • 中间层：考虑的因素、决策的准则。 • 对于相邻的两层，称高层为目标层，低层为因
素层。 下面举例说明。
例1 大学毕业生就业选择问题 获得大学毕业学位的毕业生，在“双向选择”时，
用人单位与毕业生都有各自的选择标准和要求。就 毕业生来说选择单位的标准和要求是多方面的，例 如：
素相互比较的困难，以提高准确度。
判断矩阵是表示本层所有因素针对上一层某一个因素的 相对重要性的比较。判断矩阵的元素aij用Santy的1—9标 度方法给出。
心理学家认为成对比较的因素不宜超过9个，即每层 不要超过9个因素。
• 层次分析法是社会、经济系统决策中的有效工具。 其特征是合理地将定性与定量的决策结合起来， 按照思维、心理的规律把决策过程层次化、数量 化。是系统科学中常用的一种系统分析方法。
• 该方法自1982年被介绍到我国以来，以其定性与 定量相结合地处理各种决策因素的特点，以及其 系统灵活简洁的优点，迅速地在我国社会经济各 个领域内，如工程计划、资源分配、方案排序、 政策制定、冲突问题、性能评价、能源系统分析、 城市规划、经济管理、科研评价等，得到了广泛 的重视和应用。
是对难于完全定量的复杂系统作出决策的模型和方 法。
• 决策是指在面临多种方案时需要依据一定的标准选 择某一种方案。日常生活中有许多决策问题。举例

多目标决策模型：层次分析法(AHP)、代数模型、离散模型

多目标决策模型：层次分析法(AHP)、代数模型、离散模型
2
程中常是定性的。 例如：经济好，身体好的人：会将景色好作为第一选择； 中老年人：会将居住、饮食好作为第一选择； 经济不好的人：会把费用低作为第一选择。 而层次分析方法则应给出确定权重的定量分析方法。 （S3）将方案后对准则层的权重，及准则后对目标层的权重进行综合。 （S4）最终得出方案层对目标层的权重，从而作出决策。 以上步骤和方法即是 AHP 的决策分析方法。 三、确定各层次互相比较的方法——成对比较矩阵和权向量 在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因 而 Santy 等人提出：一致矩阵法 ．．．．． 即：1. 不把所有因素放在一起比较，而是两两相互比较 2. 对此时採用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，提高准确度。 因素比较方法 —— 成对比较矩阵法： 目的是，要比较某一层 n 个因素 C1 , C 2 , , C n 对上一层因素 O 的影响（例如：旅游决策解 中，比较景色等 5 个准则在选择旅游地这个目标中的重要性） 。 採用的方法是：每次取两个因素 C i 和 C j 比较其对目标因素 O 的影响，并用 aij 表示，全部 比较的结果用成对比较矩阵表示，即：
分析：
W1 W2 若重量向量 W 未知时， 则可由决策者对物体 M 1 , M 2 , , M n 之间两两相比关系， W n 主观作出比值的判断，或用Delphi（调查法）来确定这些比值，使 A 矩阵（不一定有一致性）
为已知的，并记此主观判断作出的矩阵为（主观）判断矩阵 A ，并且此 A （不一致）在不一致 的容许范围内，再依据： A 的特征根或和特征向量 W 连续地依赖于矩阵的元素 aij ，即当 aij 离 一致性的要求不太远时， A 的特征根 i 和特征值（向量）W 与一致矩阵 A 的特征根 和特征向 量 W 也相差不大的道理：由特征向量 W 求权向量 W 的方法即为特征向量法，并由此引出一致 性检查的方法。 问题：Remark 以上讨论的用求特征根来求权向量 W 的方法和思路，在理论上应解决以下问题： 1． 一致阵的性质 1 是说：一致阵的最大特征根为 n （即必要条件） ，但用特征根来求特征向量 时， 应回答充分条件： 即正互反矩阵是否存在正的最大特征根和正的特征向量？且如果正互 反矩阵 A 的最大特征根 max n 时， A 是否为一致阵？ 2． 用主观判断矩阵 A 的特征根 和特征向量 W 连续逼近一致阵 A 的特征根 和特征向量 W 时，即： 由 lim k

层次分析法分析(AHP)及实例教程

层次分析法分析(AHP)及实例教程
02
设定评价标准
根据问题背景和目标，设定合理的评价标准，如 成本、效益、风险等。
识别关键因素和指标
关键因素识别
分析影响决策目标的关键因素，如市 场需求、技术水平、资源条件等。
指标选取
针对每个关键因素，选取具体的评价 指标，如市场份额、创新能力、资源 利用率等。
构建递阶层次结构图
目标层
准则层
将决策目标作为最高层， 表示解决问题的总体目标。
层次分析法分析 (AHP)及实例教程
目录
• 层次分析法(AHP)概述 • 构建层次结构模型 • 构造判断矩阵与权重计算 • 实例教程：以某企业投资决策为例 • AHP优缺点及改进方向 • 总结与展望
01
层次分析法(AHP)概述
AHP定义与发展历程
定义
层次分析法（Analytic Hierarchy Process，简称AHP）是一种定性与定量相结合的、系统化、 层次化的分析方法。它通过将复杂问题分解为若干层次和因素，对各因素进行两两比较，构造 判断矩阵，进而计算各因素的权重，为决策问题提供定量依据。
对计算得到的权重进行一致性检 验，确保结果的合理性和准确性。
一致性检验与调整策略
一致性检验方法
通过计算一致性指标CI和随机一 致性指标RI，判断判断矩阵的一 致性。
调整策略
当判断矩阵不满足一致性要求时， 需要对判断矩阵进行调整，包括 调整元素值、重新构造判断矩阵 等方法，直至满足一致性要求。
注意事项
针对缺点提出改进措施
1 2
提高数据质量和数量
通过改进数据采集和处理方法，提高数据的质量 和数量，减少数据不准确和不完整对决策结果的 影响。
引入客观标准
在构建判断矩阵时，可以引入客观标准和量化指 标，减少主观判断对决策结果的影响。

多目标决策分析之层次分析法

必须将不同度量单位的准则，化为无量纲 统一的数量标度，并按特定的法则和逻辑 过程进行归纳与综合，才能建立各可行方 案之间具有可比性的数量关系。
效用函数正是一种统一的数量标度。
2.1.3 评价准则和效用函数
多目标决策中，任何一个方案的效果均可 以由目标准则体系的全部结果值所确定。 可行方案在每一个目标准则下，确定—个 结果值，对目标准则体系，就得到一组结 果值，并经过各目标准则的效用函数，得 出一组效用值。
方案层各方案关于目标准则体系整体的优 先权重，是通过递阶层次从下到上逐层计 算的。这一过程称为递阶层次权重解析过 程。
递阶层次权重解析过程
(1)测算每一层次关于上一层次某元素的优先 权重（相邻两层次间的权重解析）
方法： 构造判断矩阵； 计算判断矩阵的最大特征值和特征向量； 以特征向量各分量表示该层次元素的优先权 重（？），得到层次单排序。
是一种定性与定量相结合的多目标决策分析 方法。
AHP决策分析法，能有效地分析非序列型多 层次目标准则体系，是解决复杂的非结构化 的经济决策问题的重要方法，是计量经济学 的主要方法之一。
科研课题的综合评价
综合评价科研课题
成果贡献 人才培养
可行性
发展前景
实
科
优
难
研
财
用
技
势
易
究
政
价
水
发
程
周
支
值
平
挥
度
实际中，模型的层次不宜过多，每层元素一 般不宜超过9个。目的：避免模型中存在过 多元素而使主观判断比较有困难。
2. 层次元素排序的特征向量法
构建了层次结构模型，决策就转化为待评 方案（最低层）关于具有层次结构的目标 准则体系的排序问题。

运筹学多目标规划演示文稿


1， 投资第i个项目 0，不投资第i个项目
约束条件： n
i1
ai xi
A
xi 0或1（i 1,, n)
第十页，共57页。
§2 多目标规划模型及其解的概念
目标函数：何为最佳的经济效益？
（1）收益最大：
n
max f1 ( x1 ,, xn ) bi xi i 1
（2）投资最少：
n
min f2 ( x1 ,, xn ) ai xi i 1
运筹学多目标规划演示文稿
第一页，共57页。
运筹学多目标规划
第二页，共57页。
§1 多目标决策简介
一、多目标决策问题实例
• 干部评估－德、才兼备
• 教师晋升－教学、科研、论文等
• 购买冰箱－价格、质量、耗电、品牌等 • 球员选择－技术、体能、经验、心理
• 找对象－容貌、学历、气质、家庭状况
第三页，共57页。
三、多目标决策与单目标决策区别
• 点评价与向量评价
单目标： 方案dj ←评价值f(dj) 多目标：方案dj←评价向量(f1(dj)，f2(dj)…，fp(dj))
• 全序与半序: 方案di与dj之间
单目标问题: di<dj ; di=dj ; di>dj 多目标问题：除了这三种情况之外,还有一种情况
先引进一些记号，记
F1
(
f11，……，f
1 p
)
Ep
F2
(
f12，……，f
2 p
)
Ep
(1)" "：F 1 F 2意味着向量F 1的每个分量都要严格的小于向
量F
2对应的分量。即对于i
1，……，p，均有f
1 i

多目标决策层次分析法介绍ppt课件


3 简洁性 具有中等文化程度的人即可以了解层次分析法的基本原理并掌握该法的基本步骤，计算也非常简便，并且所得结果简单明确，容易被决策者了解和掌握。
以上三点体现了层次分析法的优点，该法的局限性主要表现在以下几个方面：
第一 只能从原有的方案中优选一个出来，没有办法得出更好的新方案。
第二 该法中的比较、判断以及结果的计算过程都是粗糙 的，不适用于精度较高的问题。第三 从建立层次结构模型到给出成对比较矩阵，人主观 因素对整个过程的影响很大，这就使得结果难以让 所有的决策者接受。当然采取专家群体判断的办法 是克服这个缺点的一种途径。
a) 将A的每一列向量归一化得
b) 对
c) 归一化
按行求和得
d) 计算
3 根法
步骤与和法基本相同，只是将步骤 b 改为对
按行求积并开n次方，即
三方法中，和法最为简便。看下列例子。
e) 计算
，最大特征值的近似值。
列向量归一化
求和
归一化
精确计算，得
谢谢大家！
即各方案的权重排序为
四 层次分析法的优点和局限性
1 系统性 层次分析法把研究对象作为一个系统，按照分解、比较判断、综合的思维方式进行决策 ，成为继机理分析、统计分析之后发展起来的系统分析的重要工具。
2 实用性 层次分析法把定性和定量方法结合起来，能处理许多用传统的最优化技术无法着手的实际问题，应用范围很广，同时，这种方法使得决策者与决策分析者能够相互沟通，决策者甚至可以直接应用它，这就增加了决策的有效性。
计算 可知 通过一致性检验。
对总目标的权值为：
（4）计算层次总排序权值和一致性检验
又
决策层对总目标的权向量为：
同理得， 对总目标的权值分别为：

运筹学第十章多目标决策 ppt课件


min
ck x
LP(xˆ) : s.t.
k 1
ck x ck xˆ
(k 1,L , p)
Ax b
x0
结论：
若 ˆx为 LP 的最优解，则必为有效解
若 ˆx不是 LP 的最优解，而是 y，则 y 即是有效解
例 已知一个多目标决策问题（Max问题）
max z 1=x 1 -x 2 +x 3
p
d1 =
k=1
1
fk
f
* k
r
)r
fk
f
* k
d2 =
p
(fk
f
* k
)2
k=1
d =
m ax{
1 k p
fk
f
* k
}
fk 关于
f
* k
的正偏差
dk
=fk 0,
fk*,
fk fk* >0 其余
fk 关于
f
* k
的负偏差
dk
=fk* 0,
fk,
fk fk* 0 其余
由定义知
i)
d
理 想 点 ： f* (0 , 4 2 1 0 , 2 4 0 )
( x 1 x 2 x 3 2 0 8 , 1 5 x 1 1 4 x 2 1 2 x 3 , 3 x 1 )
m in
s .t. 8 0 x1 0 125 x2 0 105 x3 0 x1 x2 x3 2 0 8 0 x1 x2 x3 2 0 8 0 1 5 x1 1 4 x2 1 2 x3 4 2 1 0 3 x1 2 4 0 x1, x2 , x3, 0
p
min wk fk (x) k 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。