2019-2020人大附中初三12月月考题(1)

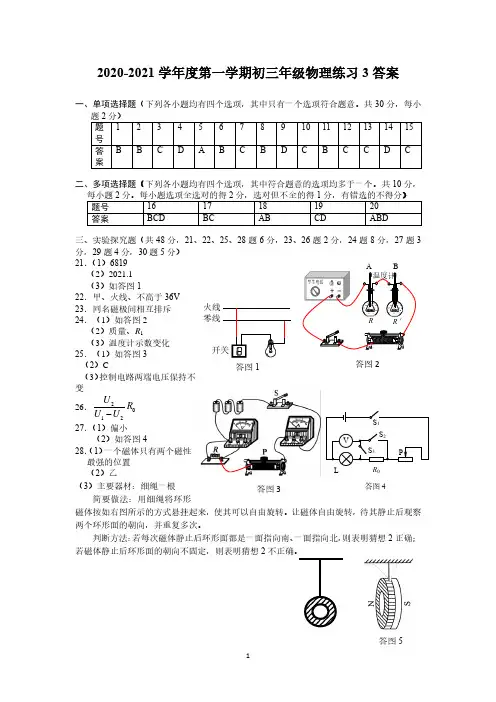
2020-2021学年度第一学期初三年级物理练习3答案一、单项选择题（下列各小题均有四个选项，其中只有一个选项符合题意。

共30分，每小题2分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 答案B BCD A B C B D C B C C D C二、多项选择题（下列各小题均有四个选项，其中符合题意的选项均多于一个。

共10分，每小题2分。

每小题选项全选对的得2分，选对但不全的得1分，有错选的不得分）题号16 17 18 19 20 答案BCD BC AB CD ABD三、实验探究题（共48分，21、22、25、28题6分，23、26题2分，24题8分，27题3分，29题4分，30题5分）21．（1）6819 （2）2021.1 （3）如答图122．甲、火线、不高于36V23．同名磁极间相互排斥 24．（1）如答图2 （2）质量、R 1（3）温度计示数变化 25．（1）如答图3（2）C （3）控制电路两端电压保持不变26．2012U R U U − 27．（1）偏小 （2）如答图4 28．（1）一个磁体只有两个磁性最强的位置 （2）乙（3）主要器材：细绳一根 简要做法：用细绳将环形磁体按如右图所示的方式悬挂起来，使其可以自由旋转。

让磁体自由旋转，待其静止后观察两个环形面的朝向，并重复多次。

判断方法：若每次磁体静止后环形面都是一面指向南、一面指向北，则表明猜想2正确；若磁体静止后环形面的朝向不固定，则表明猜想2不正确。

答图5 答图1火线 零线 开关 答图2温度计R R ′A B 答图3答图4 PVS 1R 0 S 3 L S 229．（1）C（2）0.75W30．（1）小灯泡两端的电压越大，小灯泡的电阻越大（2）小岩的结论正确。

依据：根据2=U P UI R=，而根据小灯泡的U-I 图像可知，当小灯泡两端的电压增大时，流过小灯泡的电流也随之增大，故小灯泡的实际功率一定增大，即小灯泡逐渐变亮。

北京市海淀区中国人民大学附属中学2019-2020学年九年级月考数学试题一.选择题1.我国传统文化中的“福禄寿喜”图（如图）由四个图案构成．这四个图案中既是轴对称图形，又是中心对称图形的是（）A. B. C. D.2.二次函数2y x =的图象向左平移2个单位，得到新的图象的函数表达式是（）A.22y x =+ B.22y x =-C.2(2)y x =+ D.2(2)y x =-3.在△ABC 中，∠C＝90°，以点B 为圆心，以BC 长为半径作圆，点A 与该圆的位置关系为（）A.点A 在圆外B.点A 在圆内C.点A 在圆上D.无法确定4.抛物线y ＝2x 2+4x ﹣4的对称轴是()A.直线x ＝﹣1B.直线x ＝1C.直线x ＝2D.直线x ＝﹣25.如图，在⊙O 中，点C 是»AB 上一点，若∠AOB ＝126°，则∠C 的度数为()A.127°B.117°C.63°D.54°6.二次函数y 1＝ax 2+bx +c 与一次函数y 2＝mx +n 的图象如图所示，则满足ax 2+bx +c ＞mx +n 的x 的取值范围是（）A.﹣3＜x ＜0B.x ＜﹣3或x ＞0C.x ＜﹣3D.0＜x ＜37.如图，以AB 为直径的⊙O 与弦CD 相交于点E ，且AC ＝2，AE 3CE ＝1，则弧BD 的长是()A.39π B.239π C.33π D.2338.已知一个二次函数图象经过P 1（﹣3，y 1），P 2（﹣1，y 2），P 3（1，y 3），P 4（3，y 4）四点，若y 3＜y 2＜y 4，则y 1，y 2，y 3，y 4的最值情况是（）A.y 3最小，y 1最大B.y 3最小，y 4最大C.y 1最小，y 4最大D.无法确定二.填空题9.点（2，－3）关于原点对称点P′的坐标为.10.请写出一个开口向下，且与y 轴的交点坐标为(0,2)的抛物线的表达式：_____________．11.如图，四边形ABCD 内接于⊙O ，E 为CD 延长线上一点．若∠B ＝110°，则∠ADE 的度数为_____．12.在平面直角坐标系xOy 中，函数y ＝x 2的图象经过点M(x 1，y 1)，N(x 2，y 2)两点，若﹣2＜x 1＜0，2＜x 2＜4，则y 1_____y 2.(用“＜”、“＝”或“＞”号连接)13.如图，PA ，PB 分别与⊙O 相切于A 、B 两点，点C 为劣弧AB 上任意一点，过点C 的切线分别交AP ，BP 于D ，E 两点．若AP =8，则△PDE 的周长为__________．14.如图，在平面直角坐标系xOy 中，△AOB 可以看作是△OCD 经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△OCD 得到△AOB 的过程：______．15.如图，在平面直角坐标系xOy 中，抛物线y ＝ax 2+bx +c 与x 轴交于（1，0），（3，0）两点，请写出一个满足y ＜0的x 的值_____．16.如图，⊙O 的动弦AB ，CD 相交于点E ，且AB CD =，BED α∠=(090)α︒<<︒．在①BOD α∠=，②90OAB α∠=︒-，③12ABC α∠=中，一定成立的是____________（填序号）．三.解答题17.如图，∠DAB＝∠EAC，AB＝AD，AC＝AE.求证：BC＝DE.18.已知一抛物线过点(﹣3，0)、(﹣2，﹣6)，且对称轴是x＝﹣1.求该抛物线的解析式.19.已知二次函数y＝ax2+bx+c(a≠0)中，函数y与自变量x的部分对应值如表：x…﹣2﹣102…y…﹣3﹣4﹣35…(1)求二次函数的表达式，并写出这个二次函数图象的顶点坐标；(2)求出该函数图象与x轴的交点坐标.20.下面是小东设计的“作圆的一个内接矩形，并使其对角线的夹角为60°”的尺规作图过程已知：⊙O求作：矩形ABCD，使得矩形ABCD内接于⊙O，且其对角线AC，BD的夹角为60°．作法：如图①作⊙O的直径AC；②以点A为圆心，AO长为半径画弧，交直线AC上方的圆弧于点B；③连接BO并延长交⊙O于点D；所以四边形ABCD就是所求作的矩形.根据小东设计的尺规作图过程，(1)使用直尺和圆规，补全图形(保留作图痕迹)；(2)完成下面的证明．证明：∵点A，C都在⊙O上，∴OA=OC同理OB=OD∴四边形ABCD是平行四边形∵AC是⊙O的直径，∴∠ABC=90°（）（填推理的依据）∴四边形ABCD是矩形∵AB==BO，∴四边形ABCD四所求作的矩形21.如图，AB是⊙O的直径，弦CD⊥AB于点E，AM是△ACD外角∠DAF的平分线.(1)求证：AM是⊙O的切线.(2)若C是优弧ABD的中点，AD＝4，射线CO与AM交于N点，求ON的长.22.生活中看似平常的隧道设计也很精巧．如图是一张盾构隧道断面结构图，隧道内部为以O为圆心AB为直径的圆．隧道内部共分为三层，上层为排烟道，中间为行车隧道，下层为服务层．点A到顶棚的距离为0.8a，顶棚到路面的距离是3.2a，点B到路面的距离为2a．请你求出路面的宽度l．（用含a的式子表示）23.有这样一个问题：探究函数y＝(x﹣1)(x﹣2)(x﹣3)的图象与性质.小东对函数y＝(x﹣1)(x﹣2)(x﹣3)的图象与性质进行了探究.下面是小东的探究过程，请补充完成：(1)函数y＝(x﹣1)(x﹣2)(x﹣3)的自变量x的取值范围是_______；(2)下表是y与x的几组对应值.x…﹣2﹣10123456…y…m﹣24﹣600062460…①m＝_____；②若M(﹣7，﹣720)，N(n，720)为该函数图象上的两点，则n＝_____；(3)在平面直角坐标系xOy中，A(x A，y A)，B(x B，﹣y A)为该函数图象上的两点，且A为2≤x≤3范围内的最低点，A点的位置如图所示.①标出点B的位置；②画出函数y＝(x﹣1)(x﹣2)(x﹣3)(0≤x≤4)的图象.③写出直线y＝12x﹣1与②中你画出图象的交点的横坐标之和为______.24.已知直线l：y=12x+1与抛物线y＝ax2﹣2x+c(a＞0)的一个公共点A恰好在x轴上，点B(4，m)在抛物线上.(Ⅰ)用含a的代数式表示c.(Ⅱ)抛物线在A，B之间的部分(不包含点A，B)记为图形G，请结合函数图象解答：若图形G在直线l下方，求a的取值范围.25.如图1，在等边三角形ABC中，CD为中线，点Q在线段CD上运动，将线段QA绕点Q顺时针旋转，使得点A的对应点E落在射线BC上，连接BQ，设∠DAQ=α（0°＜α＜60°且α≠30°）.（1）当0°＜α＜30°时，①在图1中依题意画出图形，并求∠BQE（用含α的式子表示）；②探究线段CE，AC，CQ 之间的数量关系，并加以证明；（2）当30°＜α＜60°时，直接写出线段CE，AC，CQ 之间的数量关系.26.在平面直角坐标系xOy 中，⊙C 的半径为r ，P 是与圆心C 不重合的点，点P 关于⊙C 的限距点的定义如下：若P′为直线PC 与⊙C 的一个交点，满足r≤PP′≤2r ，则称P′为点P 关于⊙C 的限距点，如图为点P 及其关于⊙C 的限距点P′的示意图.(1)当⊙O 的半径为1时.①分别判断点M(3，4)，N(52，0)，T(1)关于⊙O 的限距点是否存在？若存在，求其坐标；②点D 的坐标为(2，0)，DE ，DF 分别切⊙O 于点E ，点F ，点P 在△DEF 的边上.若点P 关于⊙O 的限距点P′存在，求点P′的横坐标的取值范围；(2)保持(1)中D ，E ，F 三点不变，点P 在△DEF 的边上沿E→F→D→E 的方向运动，⊙C 的圆心C 的坐标为(1，0)，半径为r ，请从下面两个问题中任选一个作答.问题1：若点P 关于⊙C 的限距点P′存在，且P′随点P 的运动所形成的路径长为πr ，则r 的最小值为__________.问题2：若点P 关于⊙C 的限距点P′不存在，则r 的取值范围为_________.。

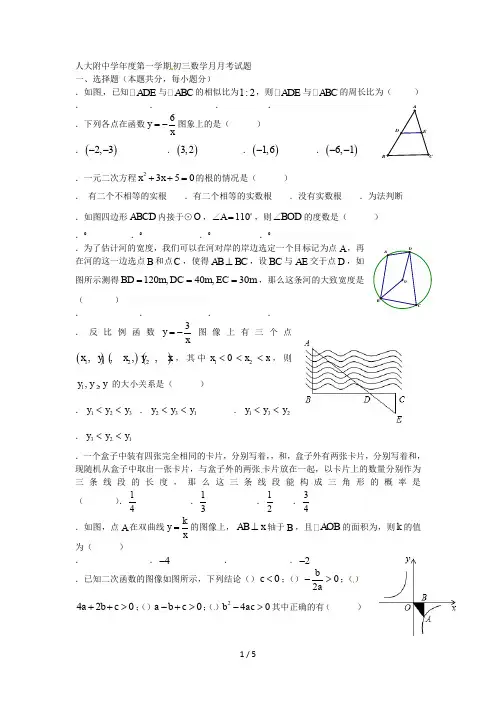
人大附中学年度第一学期初三数学月月考试题 一、选择题（本题共分，每小题分）．如图，已知ADE 与ABC 的相似比为1:2，则ADE 与ABC 的周长比为（ ）． ． ． ．．下列各点在函数6y x=-图象上的是（ ） ．()2,3-- ．()3,2 ．()1,6- ．()6,1-- ．一元二次方程2350x x ++=的根的情况是（ ）． 有二个不相等的实根 ．有二个相等的实数根 ．没有实数根 ．为法判断 ．如图四边形ABCD 内接于⊙O ，110A ∠=，则BOD ∠的度数是（ ） ．° ．° ．° ．°．为了估计河的宽度，我们可以在河对岸的岸边选定一个目标记为点A ，再在河的这一边选点B 和点C ，使得AB BC ⊥，设BC 与AE 交于点D ，如图所示测得120,40,30BD m DC m EC m ===，那么这条河的大致宽度是（ ）． ． ． ．．反比例函数3y x=-图像上有三个点()()()112233,,,,,x y x y x y ，其中1230x x x <<<，则123,,y y y 的大小关系是（ ）．123y y y << ．231y y y << ．132y y y <<．321y y y <<．一个盒子中装有四张完全相同的卡片，分别写着，，和，盒子外有两张卡片，分别写着和，现随机从盒子中取出一张卡片，与盒子外的两张卡片放在一起，以卡片上的数量分别作为三条线段的长度，那么这三条线段能构成三角形的概率是（ ）．41 ．31 ．21 ．43．如图，点A 在双曲线ky x=的图像上，AB x ⊥轴于B ，且AOB 的面积为，则k 的值为（ ）． ．4- ． ．2- ．已知二次函数的图像如图所示，下列结论（）0c <；（）02ba->；（）420a b c ++>；（）0a b c -+>；（）240b ac ->其中正确的有（ ）．个 ．个 ．个 ．个．如图，D 为腰长为的等腰直角形AOB 的腰AC 延长线上的动点，E 为底边BC 延长线上的动点，135AED ∠=，若,C E xC D y ==，则y 关于x 的图像大致是（ ）二、填空题（本题共分，每小题分）．方程2210x x -+=的解是 ．.将二次函数243y x x =-+化为()2y x h k =-+的形式，则h k +．．在平面直角坐标系xOy 中，()()1,2,4,2A B 连接AB ，写出一个函数，使它的图象与线段AB 有公共点,那么这个函数的表达式为 ．.已知抛物线254y x x =-+交x 轴于A B ，两点，交y 轴于C ，则ABC 的面积为． .如图，OA 是⊙O 的直径，6OA =，CD 是圆B 的切线，D 为切点30DOC ∠=，则点C 的坐标为．．如图，已知Rt ABC 中，90ACB ∠=，B A ∠>∠，在ABC 内找一点E ，使得EBC 和ABC 相似，小聪的做法是：取AB 边上的中线CD ，作BE CD ⊥，垂足为E ，则EBC 和ABC 相似。

2019-2020学年度第一学期初三年级数学练习1 2019.8一、选择题（本题共24分，每小题3分）第1-8题均有四个选项，符合题意的选项只有一个1、二次函数2(1)3y x =−− 的图象的顶点坐标是（ ） A 、（1,3） B 、（1，-3） C 、（-1,3） D 、（-1，-3） 2、一次函数53y x =−+的图象不经过的象限是（ ）A 、第一象限B 、第二象限C 、第三象限D 、（第四象限3、如图，正方形ABCD 的边长为2，E 是BC 的中点，DF ⊥AE,与AB 交于点F ，则DF 的长为（ ）A 、5B 、6C 、22D 、3 4、下列方程中，有两个不相等的实数根的是（ ）A 、220x += B 、21)0x −=（ C 、2+210x x −= D 、2++50x x =5、在十三届全国人大一次会议记者会上，中国科技部部长表示，2017年我国新能源汽车保有量已居于世界前列，2015年和2017年我国新能源汽车保有量如图所示，设我国2015至2017年新能源汽车保有量年平均增长率为x,依题意，可列方程为：（ ）A 、45.112)172.9x −=（ B 、45.11+2)172.9x =（ C 、245.11)172.9x −=（ D 、245.11+)172.9x =（6、要判断一个四边形是否为矩形，下面是4位同学拟定的方案，其中正确的是（ ） A 、测量两组对边是否分别相等 B 、测量两条对角线是否互相垂直平分 C 、测量其中三个内角是否都为直角D 、测量两条对角线是否相等7、已知二次函数2(0)y ax bx c a =++≠的图象如右图所示，以下结论正确的是（ ）A 、0a > ，函数值y 有最大值；B 、该函数的图象关于直线x=1对称；C 、当y=-2时，自变量x 的值等于0；D 、当x=-3和x=1时函数值y 都等于0.8、运算能力是一项重要的数学能力，王老师为帮助学生诊断和改进运算中的问题，对全班学生进行了三次运算测试，下面的气泡图中，描述了其中5位同学的测试成绩（气泡圆的圆心横、纵坐标分别表示第一次和第二次测试成绩，气泡的大小表示三次成绩的平均分的高低，气泡越大平均分越高。

2023-2024学年度第一学期初三年级练习3数学一、 单选题（每题2分，共16分）1．下列四个图形中，是中心对称图形的是（ ） A ．B ．C ．D ．2．将抛物线y =12(x +3)2−4先向右平移2个单位，再向上平移3个单位，那么平移后所得新抛物线的表达式是（ ）． 3．如图，圆心角∠AOB =100°，则∠ACB 的度数是（ ）A ．70°B ．55°C ．125°D ．130°4．利用图形的旋转可以设计出许多美丽的图案．右面图2中的图案可以由图1中的基本图案以点O 为旋转中心，顺时针（或逆时针）旋转角α，依次旋转若干次形成，则旋转角α的值不可能是（ ） A ．36°B ．72°C ．144°D ．216°5．已知点A (−3,y 1)，B (1,y 2)，C (4,y 3)在抛物线y =−(x −2)2+5上，则y 1，y 2，y 3的大小关系是（ ）A ．y 1<y 2<y 3B ．y 2<y 3<y 1C ．y 1<y 3<y 2D ．y 3<y 1<y 26．如图，AB 是⊙O 的一条弦，点C 是⊙O 上一动点，且∠ACB =30°，点E ，F 分别是AC,BC 的中点，直线EF 与⊙O 交于G ，H 两点，若⊙O 的半径是4，则GE +FH 的最大值是（ ） A ．5B ．6C ．7D ．8则下列结论正确的有（ ） ①a >0； ②c =−2；③抛物线的对称轴为直线x =1；④方程ax 2+bx +c =0的两个根满足−1<x 1<0，223x <<． A ．1个B ．2个C ．3个D ．4个8．下面三个问题中都有两个变量y 与x ：①小清去香山观赏红叶，他登顶所用的时间y min 与平均速度m/min x ； ②用绳子围成周长为10m 的矩形，矩形的一边长x m 与它的面积y m 2； ③正方形边框的边长cm x 与面积y cm 2；其中，变量y 与x 之间的函数关系（不考虑自变量取值范围）可用如图所示的函数图象表示的有（ ） A ．① B ．② C ．③ D ．②③二、填空题（每题2分，共16分）12．若关于x的一元二次方程ax2+x+2=0有两个不相等的实数根，则a的取值范围是．13．写出一个函数值有最大值，且最大值是2的二次函数解析式．14．如图，在平面直角坐标系xOy中，点A，B的坐标分别是(2,0)，(3,3)，⊙M是△OAB的外接圆，则点M的坐标为．15．《九章算术》是我国古代数学名著，也是古代东方数学的代表作之一．书中记载了一个问题：“今有勾五步，股十二步，问勾中容圆半径几何？”译文：“如图，今有直角三角形，勾（短直角边）长为5步，股（长直角边）长为12步，问该直角三角形能容纳的圆（内切圆）的半径是多少步？”根据题意，该直角三角形内切圆的半径为步．16．如图，在平面直角坐标系xOy中，直线AB过点A(−4,0)、B(0,4)，⊙O的半径为1（O 为坐标原点），点P在直线AB上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为．三、解答题(本题共68分.第17题-22题每小题5分，第23-26题每题6分，第27-28题每题7分.）17．解方程：x2−2x−8=0.18．求证：圆内接四边形的对角互补．己知：如图，四边形ABCD内接于⊙O．求证：∠B AD+∠B CD = 180°请根据上图中的辅助线，完成定理的证明过程.证明：19．如图，△ABC内接于⊙O，AE是⊙O的直径，AE⊥BC，垂足为D，求证：∠ABO=∠CAE．20．在平面直角坐标系xOy中，抛物线y=a(x−2)2−1经过点(4,3)．(1)求该抛物线的表达式；(2)在坐标系中画出该函数图象，并结合函数图象回答，当y>0时，x的取值范围是_____________________．21．已知关于x的一元二次方程x2−(m−4)x+3−m=0．(1)求证：该方程总有两个实数根；(2)若该方程恰有一个实数根为非负数，求m的取值范围．22．已知：⊙O和圆外一点P，求作：过点P的⊙O的切线．作法：①连接OP；OP长为半径画弧，两弧交于M，N两点，连接MN，交OP于②分别以O，P为圆心，大于12点C．③以C为圆心，OC长为半径作⊙C，交⊙O于点A，B；④作直线PA，PB．所以直线PA，PB为⊙O的切线．(1)使用直尺和圆规，依作法补全图形（保留作图痕迹）；(2)完成下面的证明．证明：连接MP，MO，NP，NO，OA，OB．∵MP=MO，NP=NO，∴MN是线段OP的垂直平分线（______）（填推理的依据）．=．∴CP CO∵OP为⊙O的直径，A，B在⊙C上∴∠OAP=∠OBP=90°（______）（填推理的依据）．∴半径OA⊥AP，半径OB⊥BP．∴直线PA，PB为⊙O的切线（______）（填推理的依据）．．实心球投掷后的运动轨迹可以看作是抛物线的一部分．甲、乙两人分别进行了一次投掷，从投掷到着陆的过程中，通过测量得到实心球的竖直高度y（单位：m）与水平距离x的几组数据如下：建立如图所示的平面直角坐标系，绘制图象如下：信息2：甲、乙两人投掷时，出手高度相同；信息3：乙投掷后，实心球的水平距离为3.5m时达到了竖直高度的最大值2.85m．根据以上信息，回答问题：(1)直接写出甲投掷的实心球竖直高度的最大值_________(2)求甲投掷的实心球运动轨迹所满足的函数关系；(3)记甲实心球成绩为d1，乙实心球成绩为d2，则d1_________d2（填“>”、“<”或“=”）．26．在平面直角坐标系xOy 中，P (x 1,y 1)，Q (x 2,y 2)是抛物线y =x 2−2mx +m 2−1上任意两点．(1)求抛物线的顶点坐标（用含m 的式子表示）；(2)若x 1=m −2，x 2=m +2，比较y 1与y 2的大小，并说明理由； (3)若对于−1≤x 1<4，x 2=4，都有y 1≤y 2，直接写出m 的取值范围．27．如图，在△ABC 中，90BAC ∠=︒，1AB AC ==，延长CB ，并将射线CB 绕点C 逆时针旋转90°得到射线l ，D 为射线l 上一动点，点E 在线段CB 的延长线上，且BE CD =，连接DE ，过点A 作AM DE ⊥于M ．（1）依题意补全图1，并用等式表示线段DM 与ME 之间的数量关系，并证明； （2）取BE 的中点N ，连接AN ，添加一个条件：CD 的长为_______，使得12AN DE =成立，并证明．图1 备用图lCD lC28．在平面直角坐标系xOy 中，⊙O 的半径为2．点P ，Q 为⊙O 外两点，给出如下定义：若⊙O 上存在点M ，N ，使得以P ，Q ，M ，N 为顶点的四边形为矩形，则称点P ，Q 是⊙O 的“成对关联点”．（1）如图，点A ，B ，C ，D 横、纵坐标都是整数．在点B ，C ，D 中，与点A 组成 ⊙O 的“成对关联点”的点是 ；（2）点(),E t t 在第一象限，点F 与点E 关于x 轴对称．若点E ，F 是⊙O 的“成对关联点”，直接写出t 的取值范围；（3）点G 在y 轴上．若直线y = 4上存在点H ，使得点G ，H 是⊙O 的“成对关联点”，直接写出点G 的纵坐标G y 的取值范围．2023-2024学年度第一学期初三年级数学练习3参考答案及评分标准一、选择题（每题2分，共16分）A二、填空题（每题2分，共16分）a<三、解答题17．解：方法一：x2−2x−8=0(x−4)(x+2)=0．…………………………3分40x−=或20x+=．∴x1=4，x2=−2；…………………………5分方法二：x2−2x−8=0移项，得x2−2x=8．配方，得x2−2x+1=9(x−1)2=9．…………………………3分直接开平方，得x−1=±3．∴x1=4，x2=−2；…………………………5分方法三：x2−2x−8=01,2,8a b c==−=−．Δ=b2−4ac=(−2)2−4×1×(−8)=36>0．…………………………1分∴x=2±√362×1=2±62…………………………3分∴x1=4，x2=−2．…………………………5分18． 证明：作直径AE ，连接BE,DE. ……………………1分 ∵AE 为☉O 直径∴∠ADE=∠ABE=90° ……………………2分 ∴∠DAE+∠DEA=90°，∠BAE+∠BEA=90° ∴∠DAE+∠DEA+∠BAE+∠BEA=180°即∠DAB ＋∠DEB=180° ……………………3分 ∵弧BD=弧BD∴∠DCB=∠DEB ……………………4分 ∴∠DAB+∠DCB=180° ……………………5分19．证明：∵△ABC 内接于⊙O ，AE 是⊙O 的直径，AE ⊥BC ，∴BE⏜=CE ⏜， ……………………2分 ∴∠BAE =∠CAE ， ……………………4分 ∵OB =OA ， ∴∠ABO =∠OAB ，∴∠ABO =∠CAE ． ……………………5分20．（1）∵ 抛物线y =a (x −2)2−1经过点(4,3)，∴ 4a −1=3， ………………………1分 解得：a =1∴ 该抛物线的表达式为y =(x −2)2−1． ……………………2分 （2）函数图象：略 ………………………3分 范围：x ＜1或x ＞3 ………………………5分21．（1）解：∵x 2−(m −4)x +3−m =0，∴Δ=[−(m −4)]2−4(3−m )=m 2−4m +4=(m −2)2≥0，………………2分 ∴该方程总有两个实数根； ………………3分 （2）解：∵x 2−(m −4)x +3−m =0， ∴(x +1)(x +3−m )=0，解得，x 1=−1，x 2=m −3， ………………4分∵该方程恰有一个实数根为非负数，∴m−3≥0，解得，m≥3，∴m的取值范围为m≥3．………………5分22、（1）解：如图，PA、PB即为所作，………………2分；（2）到线段两个端点的距离相等的点在这条线段的垂直平分线上………………3分直径所对的圆周角是直角………………4分经过半径的外端，且垂直于这条半径的直线是圆的切线………………5分23．解：设2021年技术改造后增长率为x，………………1分∴5000(1+x)2=11250，………………3分解得：x=0.5或x=−2.5（不合题意，舍去），∴2021年技术改造后每年的增长率为50%，………………4分∴2024年产品产量为11250×(1+50%)=16875>16500．………………5分答：保持这样的增长率，到2024年能完成公司的五年规划．………………6分24．（1）解：连接OE，…………………………1分∵AE平分∠BAC，∠=∠，∴BAE EAC∵AO=EO，∴∠OEA=∠OAE，∴∠OEA=∠EAC，∴OE∥AC，∴OE⊥PQ，…………………………2分且O E为☉O半径，∴直线PQ是⊙O的切线；…………………………3分（2）解：过点O作OF AD⊥，交AD与点F，∵AD=6，AD=3，…………………………4 分由垂径定理得到AF=FD=12∵OE∥AC，OE⊥PQ，OE=AC，∴四边形OECF是矩形，∵EC=2，∴EC=OF=2，∴AO=√AF2+OF2=√33+22=√13，…………………………5 分∴OE=FC=√13，∴AC=AF+FC=3+√13，∴CD=AC−AD=3+√13−6=√13−3．…………………………6 分25．（1）3.31m；…………………………1 分（2）解：设甲投掷的实心球运动轨迹所满足的函数关系式为：y=a(x−4)2+3.31，将(0，1.87)代入关系式得：16a+3.31=1.87，…………………………2 分解得：a=−0.09，…………………………3分∴甲投掷的实心球运动轨迹所满足的函数关系式为y=−0.09(x−4)2+3.31；…………………………4 分（3）>．…………………………6 分26．（1）解：∵y=x2−2mx+m2−1=(x−m)2−1∴抛物线顶点坐标为(m,−1)．…………………………2 分（2）将x1=m−2代入y=(x−m)2−1得y1=3将x2=m+2代入y=(x−m)2−1得y2=3…………………………3 分∴y1=y2…………………………4 分（3）m≤3．…………………………6 分227．（本题满分7分）（1）补全图形如下图，…………………………1分DM与ME之间的数量关系为DM=ME. …………………………2分证明：连接AE，AD，∵∠BAC=90°，AB=AC，∴∠ABC=∠ACB=45°．∴∠ABE=180°-∠ABC=135°．∵由旋转，∠BCD=90°，∴∠ACD=∠ACB+∠BCD=135°．∴∠ABE=∠ACD．∵AB=AC，BE=CD，∴△ABE≌△ACD．∴AE=AD．∵AM⊥DE于M，∴DM=EM．…………………………3分（2）CD=…………………………4分证明：连接AD，AE，BM.∵AB=AC=1，∠BAC=90°，∴BC=．∵BE CD==，∴BE BC=．∵由（1）得DM=EM，∴BM是△CDE的中位线．lCDE∴12BM CD=，BM∥CD.∴∠EBM=∠ECD=90°．∵∠ABE=135°，∴∠ABM=135°=∠ABE．∵N为BE中点，∴1122BN BE CD==．∴BM=BN．∵AB=AB，∴△ABN≌△ABM．…………………………6分∴AN=AM．∵由（1），△ABE≌△ACD，∴∠EAB=∠DAC，AD=AE．∵∠BAC=∠DAC+∠DAB=90°，∴∠EAD=90°．∵DM=EM，∴12AM DE=．∴12AN DE=．…………………………7分28.（本题满分7分）解：（1）B，C. ………………2分（2＜t≤2. ………………5分（3）4＜Gy≤2+2 3. ………………7分。

2023-2024学年北京市人大附中丰台校区九年级（上）月考数学试卷（12月份）一、选择题：本题共8小题，每小题2分，共16分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.下列四个图形中，是中心对称图形的是()A. B. C. D.2.将抛物线先向右平移2个单位，再向上平移3个单位，那么平移后所得新抛物线的表达式是()A. B.C.D.3.如图，圆心角，则的度数是()A. B. C. D.4.利用图形的旋转可以设计出许多美丽的图案.如图2中的图案是由图1所示的基本图案以点O 为旋转中心，顺时针或逆时针旋转角度，依次旋转五次而组成，则旋转角的值不可能是()A. B.C. D.5.已知点，，在抛物线上，则，，的大小关系是()A.B.C.D.6.如图，AB是的一条弦，点C是上一动点，且，点E，F分别是AC，BC的中点，直线EF与交于G，H两点，若的半径是4，则的最大值是()A.5B.6C.7D.87.抛物线上，部分点的横坐标x与纵坐标y的对应值如表：x……0123……y……11……则下列结论正确的有()①；②；③抛物线的对称轴为直线；④方程的两个根满足，A.1个B.2个C.3个D.4个8.下面三个问题中都有两个变量y与x：①小清去香山观赏红叶，他登顶所用的时间与平均速度；②用绳子围成周长为10m的矩形，矩形的一边长x m与它的面积；③正方形边框的边长x cm与面积；其中，变量y与x之间的函数关系不考虑自变量取值范围可用如图所示的函数图象表示的有()A.①B.②C.③D.②③二、填空题：本题共8小题，每小题2分，共16分。

9.方程的解是______.10.一个扇形的弧长为，半径为6，则此扇形的圆心角度数为______，此扇形的面积为______.11.如图，AB是半径为4的的弦，于点C，交于点D，若，则弦AB为______.12.若关于x的一元二次方程有两个不相等的实数根，则a的取值范围是______.13.写出一个函数值有最大值，且最大值是2的二次函数解析式______.14.如图，在平面直角坐标系xOy中，点A，B的坐标分别是，，是的外接圆，则点M的坐标为______.15.《九章算术》是我国古代数学名著，也是古代东方数学的代表作之一.书中记载了一个问题：“今有勾五步，股十二步，问勾中容圆半径几何？”译文：“如图，今有直角三角形，勾短直角边长为5步，股长直角边长为12步，问该直角三角形能容纳的圆内切圆的半径是多少步？”根据题意，该直角三角形内切圆的半径为______步.16.如图，在平面直角坐标系xOy中，直线AB经过点、，的半径为为坐标原点，点P在直线AB上，过点P作的一条切线PQ，Q为切点，则切线长PQ的最小值为______.三、计算题：本大题共1小题，共5分。

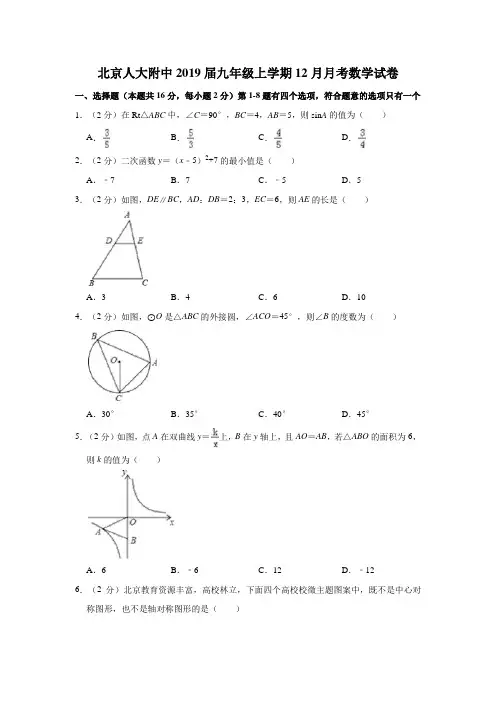
北京人大附中2019届九年级上学期12月月考数学试卷一、选择题（本题共16分，每小题2分）第1-8题有四个选项，符合题意的选项只有一个1．（2分）在Rt△ABC中，∠C＝90°，BC＝4，AB＝5，则sin A的值为（）A．B．C．D．2．（2分）二次函数y＝（x﹣5）2+7的最小值是（）A．﹣7B．7C．﹣5D．53．（2分）如图，DE∥BC，AD：DB＝2：3，EC＝6，则AE的长是（）A．3B．4C．6D．104．（2分）如图，⊙O是△ABC的外接圆，∠ACO＝45°，则∠B的度数为（）A．30°B．35°C．40°D．45°5．（2分）如图，点A在双曲线y＝上，B在y轴上，且AO＝AB，若△ABO的面积为6，则k的值为（）A．6B．﹣6C．12D．﹣126．（2分）北京教育资源丰富，高校林立，下面四个高校校徵主题图案中，既不是中心对称图形，也不是轴对称图形的是（）A．北京林业大学B．北京体育大学C．北京大学D．中国人民大学7．（2分）如图，小明在地面上放了一个平面镜，选择合适的位置，刚好在平面镜中看到旗杆的顶部，此时小明与平面镜的水平距离为2米，旗杆底部与平面镜的水平距离为12米，若小明的眼晴与地面的距离为1.5米，则旗杆的高度为（）A．9B．12C．14D．188．（2分）根据研究，人体内血乳酸浓度升高是运动后感觉疲劳的重要原因，运动员未运动时，体内血乳酸浓度水平通常在40mg/L以下；如果血乳酸浓度降到50mg/L以下，运动员就基本消除了疲劳，体育科研工作者根据实验数据，绘制了一副图象，它反映了运动员进行高强度运动后，体内血乳酸浓度随时间变化而变化的函数关系．下列叙述正确的是（）A．运动后40min时，采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同B．运动员高强度运动后，最高血乳酸浓度大约为250mg/LC．采用慢跑活动方式放松时，运动员必须慢跑70min后才能基本消除疲芳D．运动员进行完剧烈运动，为了更快达到消除疲劳的效果，应该采用跑活动方式来放松二、填空题（本题共16分，每小题2分）9．（2分）sin A＝，则锐角A＝度．10．（2分）如图，AB∥CD，AB＝CD，线段AD与BC交于点M，△AMB的周长为2，则△CMD的周长为．11．（2分）已知点P（﹣4，y1）和Q（﹣1，y2）在反比例函数y＝的图象上，则y1与y2的大小关系为y1y2（填“＞”，“＜”或“＝”）12．（2分）将抛物线y＝x2，沿x轴向左平移1个单位后，得到的物线的解析式是．13．（2分）如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P＝50°，则∠BAC＝．14．（2分）如图，边长为3的正方形OABC的顶点A，C分别在x轴y轴的正半轴上，若反比例数y＝的图象与正方形OABC的边有公共点，则k的取值范围是．15．（2分）如图1，在线段AB上找一点C，C把AB分为AC和CB两段，其中BC是较小的一段，如果，那么称线段AB被点C黄金分割．黄金分割经常被应用在建筑雪等艺术领域．如图2，在“附中学子故宫行”活动中，同学们沿着紫禁城的中轴线，从内金水桥走到了太和殿，领略了古代建筑的美轮美奂，太和门位于太和殿于内金水桥之间靠近内金水桥的一侧，三个建筑的位置关系满足黄金分割，已知太和殿到内金水桥的距离约为100丈，设太和门到太和殿之间的距离为x丈，要求x，则可列方程为．16．（2分）如图，点E在△DBC边DB上，点A在△DBC内部，∠DAE＝∠BAC＝90°，AD＝AE，AB＝AC．给出下列结论，其中正确的是（填序号）①BD⊥CE②∠DCB﹣∠ABD＝45°③CE﹣BE＝AD④BE2+CD2＝2（AD2+AB2）三、解答题（本题共6分，第17-22题，每小题5分，第236题，每小题5分，第27-题，每小题5分）17．（5分）计算：tan60°﹣4sin30°cos45°18．（5分）如图，在由边长为1个单位的长度的小正方形组成的网格图中，已知点O及△ABC的顶点均为网格线的交点（1）在给定网格中，以O为位似中心，将△ABC放大为原来的三倍，得到请△A'B'C'，请画出△A'B'C'；（2）B'C'的长度为单位长度，△A′B′C′的面积为平方单位．19．（5分）如图，△ABC中，点D在AB上，∠ACD＝∠ABC．（1）求证：△ACD∽△ABC；（2）若AD＝2，AB＝6，求AC的长．20．（5分）关于x的一元二次方程x2+（2m﹣1）x+m2﹣1＝0有两个不相等的实数根（1）求m的取值范围；（2）若m是满足条件的最大整数，求方程的根．21．（5分）在平面直角坐标系中，已知抛物线y＝x2+bx+c的对称轴为x＝2，且其顶点在直线y＝﹣2x+2上．（1）直接写出抛物线的顶点坐标；（2）求抛物线的解析式．22．（5分）工厂对某种新型材料进行加工，首先要将其加温，使这种材料保持在一定温度范围内方可加工，如图是在这种材料的加工过程中，该材料的温度y（℃）时间x（min）变化的数图象，已知该材料，初始温度为15℃，在温度上升阶段，y与x成一次函数关系，在第5分钟温度达到60℃后停止加温，在温度下降阶段，y与x成反比例关系．（1）写出该材料温度上升和下降阶段，y与x的函数关系式：①上升阶段：当0≤x≤5时，y＝；②下降阶段：当x＞5时，y．（2）根据工艺要求，当材料的温度不低于30℃，可以进行产品加工，请问在图中所示的温度变化过程中，可以进行加工多长时间？23．（6分）如图，AB是⊙O的直径，过点B做⊙O的切线BC，点D为⊙O上一点，且CD＝CB，连结DO并延长交CB的延长线于点E．（1）求证：CD是⊙O的切线；（2）连接AC，若BE＝4，DE＝8，求线段AC的长．24．（6分）在平面直角坐标系xOy中，反比例数y＝的图象过点A（6，1）．（1）求反比例数的表达式；（2）过点A的直线与反比例数y＝图象的另一个交点为B，与y轴交点交于点P．①若点P为原点，直接写出点B的坐标；②若PA＝2PB，求点P的坐标．25．（6分）如图1，Rt△ABC中，∠ACB＝90°，点D为AB边上的动点（点D不与点A，点B重合），过点D作ED⊥CD交直线AC于点E，已知∠A＝30°，AB＝4cm，在点D 由点A到点B运动的过程中，设AD＝xcm，AE＝ycm．小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小东的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x与y的几组值，如下表：（说明：补全表格时相关数值保留一位小数）（2）在如图2的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当AE＝AD时，AD的长度约为cm．26．（6分）在平面直角坐标系xOy中抛物线y＝ax2﹣2ax+3（a≠0）的顶点A在第一象限，它的对称轴与x轴交于点B，△AOB为等腰直角三角形（1）写出抛物线的对称轴为直线；（2）求出抛物线的解析式；（3）垂直于y轴的直线L与该抛物线交于点P（x1，y1），Q（x2，y2）其中x1＜x2，直线L与函数y＝（x＞0）的图象交于点R（x3，y3），若，求x1+x2+x3的取值范围．27．（7分）如图，∠MON＝α（0＜α＜90°），A为OM上一点（不与O重合），点A关于直线ON的对称点为B，AB与ON交于点C，P为直线ON上一点（不与O，C重合）将射线PB绕点P顺时针旋转β角，其中2α+β＝180°，所得到的射线与直线OM交于点Q这个问题中，点的位置和角的大小都不确定，在这里我们仅研究两种特殊情况，一般的情况留给同学们深入探索（1）如图1，当α＝45°时，此时β＝90°，若点P在线段OC的延长线上①依题意补全图形；②求∠PQA﹣∠PBA的值；（2）如图2，当α＝60°，点P在线段CO的延长线上时，用等式表示线段OC，OP，AQ之间的数量关系，并证明．28．（7分）对于平面直角坐标系xOy中的⊙C和点P，给出如下定义若在⊙C上存在一点Q，使得△PCQ是以CQ为底边的等腰三角形且底角∠PCQ≤60°，则称点P为⊙C的“邻零点”，（1）当⊙O的半径为2时，①在点P1（﹣2，0），P2（1，﹣1），P3（0，3）中，⊙O的“邻零点”是；②点P在直线y＝﹣x上，若P为⊙O的“邻零点”，求点P的横坐标x P的取值范围．（2）⊙C的圆心在x轴上，半径为4，直线y＝2x+2与x轴，y轴分别交于点A，B，若线段AB上的点都是⊙C的“邻零点”，直接写出圆心C的横坐标t的取值范围．。

2020-2021学年度第一学期初三年级数学练习32020.12考生须知1.本试卷共7页,共三道大题,25道小题,满分100分。

考试时间100分钟2.在试卷和答题卡上准确填写学校名称、姓名和准考证号3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答5.考试结束,将答题卡和草稿纸一并交回.一、选择题(本题共24分，每小题3分)第1-8题均有四个选项,符合题意的选项只有．．一个1.《北京市生活垃圾管理条例》对生活垃圾分类提出更高要求,于2020年5月1日起施行，施行的目的在于加强生活垃圾管理，改善坡乡环境，保障人体健康.下列垃圾分类标志中，既是轴对称图形，又是中心对称图形的是（）可回收垃圾其他垃圾有害垃圾厨余垃圾（A）（B）（C）（D）2.如图，已知D ，E 分别在直线AB ，AC 上，且DE ∥BC ，若21=AB AD ，则ACAE的值是（）A.21B.31 C.2D.913.已知蓄电池的电压为定值，使用蓄电池时，电流I (单位:A)与电阻R(单位:Ω)是反比例函数关系，它的图象如图所示.则用电阻R 表示电流I 的函数表达式为（）A.RI 3=B.RI 6－= C.RI 3－= D.RI 6=4.一元二次方程x x 22=的根是（）A.=x 2B.=x 0C.=1x 2，=2x 0D.221==x x 5.如图，⊙O 的半径为1，PA ，PB 是⊙O 的两条切线，切点分别为A ，B.连接OA ，OB ，AB ，PO ，若∠APB=60°，则△PAB 的周长为（）A.36 B.33 C.6D.36.如果A(2，1y )，B(3，2y )两点都在反比例函数xy 1=的图象上,那1y 与2y 的大小关系是（）A.1y ＜2y B.1y ＞2y C.1y =2y D.无法确定7.如图，以点O 为圆心，AB 为直径的半圆经过点C ，若C 为AB 的中点，若AB=4，则图中阴影部分的面积是（）A.ΠB.2+2πC.2πD.2+π8.小宇在利用描点法画二次函数c bx ax y ++=2（0≠a ）的图象时，先取自变量x 的一些值，计算出相应的函数值y ，如下表所示：x …01234…y…4－13…接着，他在描点时发现，表格中只有一组数据计算错误，他计算错误的一组数据是（）A.34==y x B.3==y x C.12－==y x D.40==y x 二、填空题(本题共24分，每小题3分)9已知34=y x ，则yyx +=.10.如图，点P 在反比例函数xky =（0＜x ）的图象上，过点P 作PM ⊥x 轴点M ，PN ⊥y 轴于点N ，若矩形PMON 的面积为2，则k 的值为.11.如图,在△ABC 中，M ，N 分别是AC ，BC 的中点，则ABNM CMNS S 四边形△=.12.在平面直角坐标系xOy 中，点A(a ，b )(a >0，b >0)在双曲线xk y 1=上.点A 关于x 轴的对称点B 在双曲线xk y 2=上，则21k k +的值为.13.如图，点A 、B 、C 、D 在⊙O 上，C 是弧BD 的中点，若∠ODC=50°，则∠BAC 的度数为.14.如图，在矩形ABCD 中，E 是边AB 的中点，连接DE 交，对角线AC 于点F ，若AB=4，AD=3，则CF 的长为.15.已知关于x 的二次函数242+=x mx y －与x 轴有公共点，则m 的取值范围是.16.如图，△ABC 是等边三角形，AB=3，点D 在AC 上，AD=2CD ，点E 在BC 的延长线上，将线段DE 绕点D 逆时针旋转90°得到线段DF ，连接AF ，若AF ∥BE,，则AF 的长为.三、解答题(本题共52分，第17-20题，每小题5分，第21-23题，每小题6分，第24-25题，每小题7分）解答应写出文字说明、演算步骤或证明过程.17.解方程：9242－－x x x =.18.如图，已知AE 平分∠BAC ，ACADAE AB =.(1)求证:∠E=∠C ；(2)若AB=9，AD=5，DC=3，求BE 的长.19.已知二次函数342+=x x y －.(1)直接写出这个函数的顶点坐标；(2)在平面直角坐标系xOy 中画出该函数的图象；(3)当0≤x ≤3时，y 的取值范围是.20.已知关于x 的方程()0222=+++m x m x .(1)求证:方程总有两个实数根；(2)若方程有一个根大于1，求m 的取值范围.21.如图，在平面直角坐标系xOy 中，已知直线l ：3－mx y =过点A(3，0)(1)求直线l 的表达式；(2)直线l 与y 轴交于点B ，点C 是双曲线xny =与直线l 的一个公共点，①若n =4，点C 在第一象限，求ACAB的值；②若1<ACAB<3，结合图象，直接写出n 的取值范围.22.如图，AB 为⊙O 的直径,点C 在OO 上，直线CP 是⊙O 的切线，过点A 作CP 的垂线，垂足为D ，交BC 的延长线于点E.(1)求证：AE=AB ；(2)若AB=10，BC=6，求线段CD 的长.23.在平面直角坐标系xOy 中，抛物线122－－mx mx y 与y 轴的交点为A.(1)求抛物线的对称轴和点A 坐标；(2)横、纵坐标都是整数的点叫做整点.已知点B(2，0)，记抛物线与直线AB 所围成的封闭区域为图形W(不含边界)①当m =1时，直接写出图形W 内的整点个数；②若图形W 内恰有1个整点，结合函数图象，求m 的取值范围.24.如图，在△ABC 中，∠ABC=45°，AD 为BC 边上的高线，E 为AD 上一点,满足DE=DC ，连接BE.（1）求证：BE=AC ；（2）取线段BC 的中点M ，连接并延长ME 到点F ，使得CF=CA ，①依题意补全图形；②证：∠CFE=∠BM ；③连接AF ，若AF ∥BC 成立，直接写出CDBD的值.25.在平面直角坐标系xOy中，对于已知的点P和图形W，若对图形以上任意两点MPM≤3PN成立，则称图形W为点P的“关联图形”.（1）已知点A(0，1)，B(1，0)①如图1，点C的坐标为(-2，0)，则点A到线段BC上的点的最短距离为，线段BC.(填“是”或“不是”)点A的“关联图形”；②点Q为x轴上一个动点，若线段BQ是点A的“关联图形”，求点Q的横坐标x的取值范围；Q（2）⊙T的圆心为(t，0)，半径为2，直线1y 与x轴，y轴分别交于G，H两点，x－若在线段GH上存在点P，使得⊙T是点P的“关联图形”，直接写出t的取值范围.图1图2备用图。

北京人大附中2019 届九年级上月考数学试卷(12 月)含答案解析一、选择题（本题共32 分，每小题 4 分）1．反比例函数y=的图象不一定经过点( )A ．（﹣ 3， 1） B．（﹣ 3，﹣ 1）C．（ 1，3）D．（，2）2．下列图形中，不是轴对称图形的是( )A ．B．C．D．3．随机抛掷一枚质地均匀的硬币两枚，两次都是正面朝上的概率是( )A ．B．C．D．4．如图，⊙ O 的直径 AB=8 ，弦 DE 经过 OB 的中点 C 且 DE ⊥ OB，则弦 DE 的长为 ( )A ． 3B． 2C． 4D． 65．如图，正△ ABC 的边长为3，以 A 为圆心， AB 为半径作弧，则图中阴影部分的面积是( )A ．B．C．﹣D． 36．如图，四边形ABCD 中， AB=AC=AD ，∠ CBD=23 °，则∠ CAD 为 ( )A ． 47°B ． 46°C． 45°D． 44°7．如图， AB 为⊙ O 的一条固定直径，自左半圆上一点C，作弦 CD⊥AB ，∠ OCD 的平分线交⊙ O 于点 E，当点 C 在左半圆（不包括 A ，B 两点）上移动时，关于点 E 的说法：①到 CD 的距离始终不变；② 位置始终不变；③ 始终平分；④位置随点 C 的移动而移动，正确的是 ( )A ．①②B．②③C．②D．④8．如图，正△ ABC 的边长为 3，点 N 在 AC 从点 A 出发，沿 A →B→C 的方向运动，到达点边上且 AN ： NC=1 ： 2，三角形边上的动点M C 时停止．设点 M 运动的路程为 x，y=MN 2，则 y 关于 x 的函数图象大致为( )A ．B．C．D．二、填空题（本题共16 分，每小题 4 分）9．如图， DE ∥BC ， AD ： DB=2 ： 3， EC=6，则 AE 的长是 __________．10．在 Rt△ABC 中，∠ C=90 °，AC=5 ， AB=13 ， tanA 的是 __________ ．11．如，用一个交叉卡（OA=OB ， OC=OD ）量零件的内孔直径AB ，若 OC：OA=1 ： 2，且量的CD=12mm ，零件的内孔直径AB 是 __________mm ．12．如，△ ABC 中， AB=AC=1 ，∠ ABC=72 °， BB 1平分∠ ABC 交 AC 于 B1， B1做 B1B 2∥BC 交 AB 于 B2，作 B2B 3平分∠ AB 2B 1交 AC 于 B3， B3作 B 3B4∥ BC 交 AB 于B4，⋯段 B1B 2的度 __________ ，段 B 2n﹣1B2n的度 __________ ．三、解答（本共30 分，每小 5 分）13．用配方法解方程：．14．算： 3sin30°2cos 45°+2tan60°cos30°．15．如，△ ABC 与△ADE 都是等腰直角三角形，且∠ BAC= ∠ DAE=90 °，找出一条与段 CE 相等的段（以中已知点的端点），画出条段并出明．16．已知 m 是方程 x 2﹣ x ﹣3=0 的根，求代数式（ 1+） ?（ m ﹣ 3）的值．17．如图，半径为 5 的⊙ O 中， AB 是直径，弦 BC=8 ，OD ⊥ AB 交 BC 于 D ，求 CD 的长及△ OCD 的面积．18．列方程或方程组解应用题：150 元，双人间每天每间 140 元，为了某酒店有三人间、双人间的客房，三人间每天每间吸引游客，实行团体入住五折优惠措施，一个50 人的旅游团优惠期间到该酒店入住，住了 一些三人间和双人间客房，若每间客房正好住满且一天共花去住宿费1510 元，则该旅行团 住了三人间和双人间客房各多少间？四、解答题（本题共20 分，每小题 5 分）19．如图，直线 y=﹣ 2x+1 分别交 x 轴， y 轴于点 A ， B ，交反比例函数 y= 的图象于点 C ， CB ： BA=2 ： 1．（1）求反比例函数 y= 的解析式；（2）若点 P 在 y 轴上且以点 B ， C ，P 为顶点的三角形与 △ AOB 相似，直接写出点 P 的坐标．20．如图，已知，在△ ABC 中，∠ ABC=90 °， BC 为⊙ O 的直径， AC 与⊙ O 交于点 D，点E 为 AB 的中点， PF⊥BC 交 BC 于点 G，交 AC 于点 F．（1）求证： ED 是⊙ O 的切线；（2）如果 CF=1， CP=2， sinA=，求⊙ O的直径BC．21 ．据报道，历经一年半的调查研究， PM 2.5 源解析已经通过专家论证．各种调查显示，机动车成为 PM 2.5 的最大来源，一辆车一天行驶 20 千米，那么这辆车每天至少就要向大气里排放 0035 千克污染物．以下是相关的统计图、表：年全年空气质量等级天数统计表空气质量等级优良轻度污中度污重度污严重污染染染染天数（天）41 135 84 47 45 13（1）请根据所给信息补全扇形统计图；（2）请你根据“年全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少？（精确到 0.01）（3）小明是社区环保志愿者，他和同学们调查了本社区的100 辆机动车，了解到其中每天出行超过 20 千米的有 40 辆．已知年机动车保有量已突破 520 万辆，请你通过计算，估计年一天中出行超过 20 千米的机动车至少要向大气里排放多少千克污染物？22．如图 1，给定锐角三角形ABC ，小明希望画正方形 DEFG ，使 D， E 位于边 BC 上，F， G 分别位于边 AC ， AB 上，他发现直接画图比较困难，于是他先画了一个正方形HIJK ，是的 H， I ，位于射线 BC 上， K 位于射线 BA 上，而不需要求 J 必须位于 AC上．这是他发现可以将正方形HIJK 通过放大或缩小得到满足要求的正方形DEFG ．阅读以上材料，回答小明接下来研究的以下问题：（1）如图 2，给定锐角三角形ABC ，画出所有长宽比为 2： 1 的长方形 DEFG ，使 D ， E 位于边 BC 上， F， G 分别位于边AC ， AB 上．（2）已知三角形 ABC 的面积为 36， BC=12 ，在第（ 1）问的条件下，求长方形 DEFG 的面积．五、解答题（本题共22 分，第 23 题 7 分，第 24 题 7 分，第 25 题 8 分）23．已知关于 x 的二次函数 y 1=x 2﹣（ m+3） x+m+2 ， y 2=﹣ x 2+bx+c ．（1）求证：方程 x 2﹣（ m+3 ） x+m+2=0 必有实根；（2）若 m 为整数， y 1 的图象与 x 轴有一个交点的横坐标 a 满足 5＜ a ＜ 7，求 m 的值；（3）在第（ 2）问的条件下，小明利用函数图象解关于x 的不等式 y 1 ＜y 2，正确解得该不等式的解 集为 3＜ x ＜4，求 y 2 的解析式．24．过正方形 ABCD 的顶点 A 任作一条直线 l （ l 不过点 B ，C ， D ） ，过点 B ，C ，D 作 l的垂线段 BF ，CG ，DH ．（ 1）如图 1，若直线 l 过线段（ 2）如图 2，若直线 l 与线段BC 的中点 E ，则 BF ： CG ： DH=__________ ．BC 相交于点 E ，则 BF ， CG ， DH 满足等量关系式 __________，请证明你的猜想；（3）如果直线 l 与线段 CB 的延长线相交，直接写出BF ， CG ， DH 满足的等量关系式__________，在直线 l 旋转一周的过程中（ l 不过点 B ， C ， D ），直接写出 y=的取值范围 __________．25．定义：在平面直角坐标系 xOy 中，给定两点 M （ x M ， y M ）， N （ x N ， y N ），对于给定的实数 a ， b ，作 a|x M ﹣x N |+b|y M ﹣ y N |为 M ， N 的权重为 a ， b 的直角距离，记为 d xy （ M ，N ），例如： d 2， 3（（ 1， 0），（ 4， 7）） =2|1﹣4|+3|0﹣ 7|=27． 特别地，权重为 1、1 的直角距离，又称为等权重距离，则记为 d （ M ，N ），例如： d（（ 1， 0），（ 4， 7）） =|1﹣4|+|0﹣ 7|=10． 根据以上定义，回答以下问题：（1） d （（ 0， 0），（﹣ 3，﹣ 2）） =__________， d 3， 2（（ 0， 0），（﹣ 1， 2）） =__________ ．（2） P 为直线 y=2x+4 上一动点，求 OP 的等权重距离的最小值及此时 P 点的坐标； （3） P 为直线 y=2x+4 上一动点， Q 为以 O 为圆心的单位圆上的动点，则 d （ P ， Q ）的最 小值是 __________ ，d 3，2（ P ， Q ）的最小值是 __________．-学年人大附中九年级（上）月考数学试卷（12 月份）一、选择题（本题共32 分，每小题 4 分）1．反比例函数 y= 的图象不一定经过点( )A ．（﹣ 3， 1） B．（﹣ 3，﹣ 1）C．（ 1，3）D．（， 2）【考点】反比例函数图象上点的坐标特征．【分析】根据反比例函数图象上点的坐标特点即可得出结论．【解答】解： A 、∵（﹣ 3）×1=﹣3≠3，∴函数图象不过此点，故本选项正确；B、∵（﹣ 3）×（﹣ 1） =3，∴函数图象过此点，故本选项错误；C、∵3×1=3 ，∴函数图象过此点，故本选项错误；D、∵×2=3，∴函数图象不过此点，故本选项错误．故选 A ．【点评】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．2．下列图形中，不是轴对称图形的是( )A ．B．C．D．【考点】轴对称图形．【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解．【解答】解： A 、不是轴对称图形，故本选项正确；B、是轴对称图形，故本选项错误；C、是轴对称图形，故本选项错误；D、是轴对称图形，故本选项错误．故选 A ．【点评】本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．3．随机抛掷一枚质地均匀的硬币两枚，两次都是正面朝上的概率是( )A ．B．C．D．【考点】列表法与树状图法．【分析】列举出所有情况，看正面都朝上的情况数占总情况数的多少即可．【解答】解：共 4 种情况，正面都朝上的情况数有 1 种，所以概率是．故选 B ．【点评】本题考查了概率的求法；用到的知识点为：概率=所求情况数与总情况数之比．得到所求的情况数是解决本题的关键．4．如图，⊙ O 的直径 AB=8 ，弦 DE 经过 OB 的中点 C 且 DE ⊥ OB，则弦 DE 的长为 ( )A ． 3B． 2C． 4D． 6【考点】垂径定理；勾股定理．【分析】连接 OD ，先求出OD 及 OC 的长，再由勾股定理求出DE 的长即可．【解答】解：连接 OD，∵⊙ O 的直径 AB=8 ，弦 DE 经过 OB 的中点 C 且 DE ⊥ OB，∴O D=4 ， OC=2， DE=2CD ．∵CD===2，∴DE=2CD=4．故选： C．【点评】本题考查的是垂径定理和勾股定理的应用，掌握垂直于弦的直径平分弦并且平分弦所对的弧是解题的关键．5．如图，正△ ABC 的边长为3，以 A 为圆心， AB 为半径作弧，则图中阴影部分的面积是( )A ．B．C．﹣D． 3【考点】扇形面积的计算．【分析】根据等边三角形的面积公式求出正△ ABC 的面积，根据扇形的面积公式S= 求出扇形的面积，求差得到答案．【解答】解：∵正△ABC 的边长为3，∴正△ ABC 的面积为×3×= ，扇形 ABC 的面积为= ，则图中阴影部分的面积是﹣．故选： C．【点评】本题考查的是等边三角形的性质和扇形的面积计算，掌握扇形的面积公式S=是解题的关键．6．如图，四边形ABCD 中， AB=AC=AD，∠ CBD=23°，则∠CAD为()A． 47°B ． 46°C． 45°D． 44°【考点】圆周角定理．【分析】先根据四边形 ABCD 中， AB=AC=AD 可知， B、 C、 D 三点在以 A 为圆心， AD 为半径的圆上，再由圆周角定理即可得出结论．【解答】解：∵四边形 ABCD 中， AB=AC=AD ，∴B 、 C、 D 三点在以 A 为圆心， AD 为半径的圆上．∵∠ CBD=23 °，∴∠ CAD=2 ∠CBD=46 °．故选 B ．【点评】本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．7．如图， AB 为⊙ O 的一条固定直径，自左半圆上一点C，作弦 CD⊥AB ，∠ OCD 的平分线交⊙ O 于点 E，当点 C 在左半圆（不包括 A ，B 两点）上移动时，关于点 E 的说法：①到 CD 的距离始终不变；② 位置始终不变；③ 始终平分；④位置随点 C 的移动而移动，正确的是 ( )A ．①②B．②③C．②D．④【考点】圆周角定理；垂径定理．【分析】连接 OE，由 CE 平分∠ OCD ，得到∠ 1=∠ 2，而∠ 1=∠ E，所以有 OE∥ CD，则OE⊥AB ，即可得到 OE 平分半圆 AEB ．【解答】解：连 OE，如图，∵CE 平分∠ OCD ，∴∠ 1=∠ 2，而OC=OE ，有∠ 1=∠ E，∴∠ 2=∠ E，∴OE∥ CD ，∵点 O 到 CD 的距离在变，∴点 E 到 CD 的距离发生变；故①错误；又∵弦 CD ⊥AB ，∴OE⊥ AB ，∴OE 平分半圆AEB ，即点 E 是半圆的中点，∴点 E 位置始终不变；故② 正确．故选 C．【点评】本题考查了圆周角定理．在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．也考查了垂径定理的推论．8．如图，正△ ABC 的边长为 3，点 N 在 AC 边上且 AN ： NC=1 ： 2，三角形边上的动点M 从点 A 出发，沿 A →B→C 的方向运动，到达点 C 时停止．设点M 运动的路程为x，y=MN 2，则 y 关于 x 的函数图象大致为 ( )A ．B．C．D．【考点】动点问题的函数图象．【分析】注意分析y 随 x 的变化而变化的趋势，而不一定要通过求解析式来解决．【解答】解：∵等边三角形ABC 的边长为3， N 为 AC 的三等分点，∴AN=1 ．∴当点 M 位于点 A 处时， x=0， y=1 ．①当动点 M 从 A 点出发到 AM=0.5 的过程中， y 随 x 的增大而减小，故排除 D ；②当动点 M 到达 C 点时， x=6 ， y=4，即此时 y 的值与点M 在点 A 处时的值不相等．故排除A 、C．故选： B．【点评】本题考查了动点问题的函数图象，解决本题应首先看清横轴和纵轴表示的量，然后根据动点的行程判断 y 的变化情况．二、填空题（本题共16 分，每小题 4 分）9．如图， DE ∥BC ， AD ： DB=2 ： 3， EC=6，则 AE 的长是 4．【考点】平行线分线段成比例．【专题】计算题．【分析】根据平行线分线段成比例定理得到=，即=，然后利用比例性质求AE ．【解答】解：∵ DE ∥ BC ，∴=，即=∴A E=4 ．故答案为 4．【点评】本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．10．在 Rt△ABC 中，∠ C=90 °，AC=5 ， AB=13 ，则 tanA 的值是．【考点】锐角三角函数的定义．【分析】根据勾股定理，可得BC 的长，根据正切函数的定义，可得答案．【解答】解：在 Rt△ABC 中，∠ C=90°，AC=5 ， AB=13 ，由勾股定理，得BC===12 ，tanA==，故答案为：．【点评】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．11．如图，用一个交叉卡钳（OA=OB ， OC=OD ）测量零件的内孔直径AB ，若 OC：OA=1 ： 2，且量的CD=12mm ，则零件的内孔直径AB 是 24mm．【考点】相似三角形的用．【】算．【分析】由于 OC： OA=OD ： OB=1 ：2，加上∠ COD= ∠ AOB ，可判断△COD ∽△ AOB ，然后利用相似比开始算出AB ．【解答】解：∵ OC：OA=OD ： OB=1 ： 2，而∠ COD= ∠ AOB ，∴△ COD ∽△ AOB ，∴= = ，∴A B=2CD=2 ×12mm=24mm ．故答案 24．【点】本考了相似三角形的用：利用点和盲区的知构建相似三角形，用相似三角形的比相等的性求物体的高度或度．12．如，△ ABC 中， AB=AC=1 ，∠ ABC=72 °， BB 1平分∠ ABC 交 AC 于 B1， B1做 B1B 2∥BC 交 AB 于 B2，作 B2B 3平分∠ AB 2B 1交 AC 于 B3， B3作 B 3B4∥ BC 交 AB 于B4，⋯段 B1B 2的度，段B2n﹣1B2n的度（）n﹣2．【考点】相似三角形的判定与性．【分析】因 B1作 B 1B2∥BC 交 AB 于 B2，于是得到△ AB 2B1∽△ ABC ，得到成比例，因AB=AC=m ，∠ ABC=72 °， BB 1平分∠ ABC 交 AC 于 B1，所以△ BCB 1和△B 2B1B 是等腰三角形，根据余弦定理，可求出BC 的，根据相似三角形段成比例，可求出 B 2B1的，同理，可求得段【解答】解：∵ AB=AC=1 ，∠ ABC=72 °， BB 1平分∠ ABC 交 AC 于 B 1，∴△ BCB 1和△B 2B1B 是等腰三角形，∵ B 1作 B1B 2∥BC 交 AB 于 B2，∴= ，2 2 22AB ?ACcos36 °，∵BC =AB +ACB2n﹣1B 2n的度．∴BC=，设 B 2B 1 是 x ，则 B 2B 是 x ．∴= ，∴x=即： B 1B 2=．同理可求出 B 2n ﹣ 1B 2n =（ n ﹣ 2） ．故答案为：，（）n ﹣ 2．【点评】 本题考查相似三角形的判定和性质，关键是知道相似三角形的对应线段成比例，以及余弦定理求出 BC 的长，找出规律求出值．三、解答题（本题共30 分，每小题 5 分）13．用配方法解方程：．【考点】 解一元二次方程 -配方法．【分析】 先把常数项﹣ 3 移项后；然后等上的两边同时乘以 2 把二次项的系数化为 1；最后左右两边同时加上一次项系数﹣ 4 的一半的平方． 【解答】 解：由原方程，得x 2﹣ 2x=3 ，等上的两边同时乘以 2，得2x ﹣4x=6 ，方程两边同时加上一次项系数一半的平方，得 x 2﹣4x+4=10 ，配方得（ x ﹣ 2） 2=10． ∴ ， ∴，．【点评】 本题考查了解一元二次方程﹣﹣配方法． 配方法的一般步骤：（ 1）把常数项移到等号的右边；（ 2）把二次项的系数化为 1；（ 3）等式两边同时加上一次项系数一半的平方．选择用配方法解一元二次方程时，最好使方程的二次项的系数为 1，一次项的系数是 2 的倍数．14．计算： 3sin30°﹣ 2cos 45°+2tan60°cos30°．【考点】 特殊角的三角函数值． 【分析】 将特殊角的三角函数值代入求解． 【解答】 解：原式 =3× ﹣ ×（ ）2+2× ×= ﹣．【点评】 本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．15．如图， △ ABC 与 △ADE 都是等腰直角三角形，且∠ BAC= ∠ DAE=90 °，请找出一条与线段 CE 相等的线段（以图中已知点的端点），画出这条线段并给出证明．【考点】 全等三角形的判定与性质；等腰直角三角形．【分析】 连接 BD ，则 BD=CE ，证明 △AEC ≌△ ADB 即可． 【解答】 解：连接 BD ，则 BD=CE ；理由：∵△ ABC 与 △ADE 都是等腰直角三角形，∴ A B=AC ， AE=AD ，∵∠ BAC= ∠DAE=90 °， ∴∠ BAD= ∠ CAE ，在△ AEC 和 △ADB 中，，∴△ AEC ≌△ ADB （ SAS ）， ∴BD=CE ．【点评】 本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解决问题的关键．16．已知 m 是方程 x 2﹣ x ﹣3=0 的根，求代数式（ 1+ ） ?（ m ﹣ 3）的值．【考点】 分式的化简求值；一元二次方程的解．m 是方程 x 2﹣ x ﹣ 3=0 的根【分析】 先根据分式混合运算的法则把原式进行化简，再根据【解答】解：原式 =?（m﹣ 3）=，2∵m 是方程 x ﹣ x﹣ 3=0 的根，∴原式 ==1．【点评】本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．17．如图，半径为 5 的⊙ O 中， AB 是直径，弦 BC=8 ，OD ⊥ AB 交 BC 于 D ，求 CD 的长及△ OCD 的面积．【考点】垂径定理；勾股定理．【分析】过点 O 作 OE⊥ CD 于点 E，根据相似三角形的判定定理可得出△ ODE∽△ BOE，再由相似三角形的对应边成比例可求出OD 的长，由勾股定理得出DE 的长，进而得出CD 的长，根据三角形的面积公式即可得出结论．【解答】解：过点 O 作 OE⊥CD 于点 E，∵B C=8 ，∴C E=BE=4 ，OE=3 ．∵OD ⊥AB ，∴∠ BEO= ∠OED=90 °，∵∠ ODE+ ∠ OBE=90 °，∠ ODE+ ∠DOE=90 °，∴∠ DOE= ∠ OBE ，∴△ ODE∽△ BDO ，∴=，即=，解得DE=，∴CD=CE ﹣ DE=4 ﹣=，∴S△OCD= CD ?OE=× ×3=．【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．18．列方程或方程组解应用题：某酒店有三人间、双人间的客房，三人间每天每间150 元，双人间每天每间 140 元，为了吸引游客，实行团体入住五折优惠措施，一个50 人的旅游团优惠期间到该酒店入住，住了一些三人间和双人间客房，若每间客房正好住满且一天共花去住宿费1510 元，则该旅行团住了三人间和双人间客房各多少间？【考点】二元一次方程组的应用．【分析】本题中的等量关系有两个：三人间所住人数+二人间所住人数 =50 人；三人间费用×0.5+二人间费用×0.5=1510 ，据此可列方程组求解．【解答】解：设三人间和双人间客房各x 间、 y 间，根据题意，得，解得．答：该旅行团住了三人间和双人间客房各8 间、 13 间．【点评】本题考查了二元一次方程组的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．利用二元一次方程组求解的应用题一般情况下题中要给出 2 个等量关系，准确的找到等量关系并用方程组表示出来是解题的关键．四、解答题（本题共 20 分，每小题 5 分）19．如图，直线 y=﹣ 2x+1 分别交 x 轴， y 轴于点 A ， B ，交反比例函数y= 的图象于点C， CB ： BA=2 ： 1．（1）求反比例函数 y= 的解析式；（2）若点 P 在 y 轴上且以点 B， C，P 为顶点的三角形与△ AOB 相似，直接写出点 P 的坐标．【考点】反比例函数与一次函数的交点问题．【分析】（1）由直线的解析式求得 A 、 B 的坐标，进而根据CB ：BA=2 ： 1 求得 C 的纵坐标，将 C 坐标代入直线y= ﹣ 2x+1 中求出横坐标，代入反比例函数y=，确定出反比例解析式；（2）分两种情况分别讨论即可求得．【解答】解：（ 1）∵直线y=﹣ 2x+1 分别交 x 轴， y 轴于点 A ， B ，∴A （，0），B（0，1），∵CB ： BA=2 ： 1，∴=，作CD⊥ x 轴于 D ，则 CD ∥OB ，∴△ ACD ∽△ ABO ，∴= ，∴= ，∴C D=3 ，把y=3 代入 y= ﹣ 2x+1，解得 x= ﹣1，∴C（﹣ 1， 3），代入 y=得，3=，∴k= ﹣ 3，∴反比例函数y=的解析式为y=﹣；（2）当△CPB ∽△ AOB 时，则= ，即 = ，∴B P=2 ，∴O P=OB+BP=1+2=3 ，∴P（ 0， 3）；当△ PCB∽△ AOB 时，则= ，∵OA=，OB=1，∴AB==，∵CB ： BA=2 ： 1，∴CB=，∴=，∴P B= ，∴O P=PB+0B= +1= ，∴P（ 0，）；故 P 的坐标为（ 0， 3）或（ 0，）．【点评】此题考查了一次函数与反比例函数的交点问题，涉及的知识有：坐标与图形性质，待定系数法确定函数解析式，一次函数与坐标轴的交点，三角形相似的性质，熟练掌握待定系数法是解本题的关键．20．如图，已知，在△ ABC 中，∠ ABC=90 °， BC 为⊙ O 的直径， AC 与⊙ O 交于点 D，点E 为 AB 的中点， PF⊥BC 交 BC 于点 G，交 AC 于点 F．（1）求证： ED 是⊙ O 的切线；（2）如果 CF=1， CP=2， sinA= ，求⊙ O 的直径 BC ．【考点】 切线的判定；相似三角形的判定与性质；解直角三角形． 【专题】 几何综合题．【分析】 （1）连接 OD ，证 OD ⊥ DE 即可．易证∠ ADB=90 °，又点 E 为 AB 的中点，得 DE=EB ．根据等腰三角形性质可证 ∠ODE= ∠ OBE=90 °，得证；（2）可证∠ A= ∠ DBC ，所以要求 BC 需先求 DC ．结合已知条件，证明 △ PDC 与 △FPC 相似可求 CD ，得解．【解答】 （1）证明：连接 OD ．∵BC 为直径，∴△ BDC 为直角三角形． 在 Rt △ ADB 中，E 为 AB 中点，∴ BE=DE ， ∴∠ EBD= ∠ EDB ．又∵ OB=OD ，∴∠ OBD= ∠ ODB ，∵∠ OBD+ ∠ ABD=90 °，∴∠ ODB+ ∠ EDB=90 °． ∴ED 是⊙ O 的切线．（2）解：∵ PF ⊥BC ，∴∠ FPC=90°﹣∠ BCP （直角三角形的两个锐角互余）．∵∠ PDC=90 °﹣∠ PDB （直径所对的圆周角是直角），∠ PDB= ∠ BCP （同弧所对的圆周角相等），∴∠ FPC=∠ PDC （等量代换）． 又∵∠ PCF 是公共角， ∴△ PCF ∽△ DCP ． ∴= ，则 PC 2=CF?CD （相似三角形的对应边成比例）． ∵CF=1 ， CP=2，∴CD=4 ．可知 sin ∠DBC=sinA=，∴= ，即 = ，∴直径 BC=5 ．【点评】此题考查了切线的判定、相似三角形的判定和性质、三角函数等知识点，综合性较强，难度偏上．21．据报道，历经一年半的调查研究，PM 2.5 源解析已经通过专家论证．各种调查显示，机动车成为 PM 2.5 的最大来源，一辆车一天行驶 20 千米，那么这辆车每天至少就要向大气里排放 0035 千克污染物．以下是相关的统计图、表：年全年空气质量等级天数统计表空气质量等级优良轻度污中度污重度污严重污染染染染天数（天）41 135 84 47 45 13（1）请根据所给信息补全扇形统计图；（2）请你根据“年全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少？（精确到 0.01）（3）小明是社区环保志愿者，他和同学们调查了本社区的100 辆机动车，了解到其中每天出行超过 20 千米的有 40 辆．已知年机动车保有量已突破 520 万辆，请你通过计算，估计年一天中出行超过 20 千米的机动车至少要向大气里排放多少千克污染物？【考点】扇形统计图；用样本估计总体；统计表；列表法与树状图法．【分析】（1）用单位 1 减去其他原因所占的百分比即可确定答案；（2）用重度污染和严重污染的天数除以所有的天数即可确定出现的频率；（3）用样本估计总体即可．【解答】解：（ 1） 31.1；（2）≈0.16．该年度重度污染和严重污染出现的频率共是0.16．（3）=7 280 0，20 千米的机动车至少要向大气里排放72800 千克污染物．估计年一天中出行超过【点评】本题考查了扇形统计图、用样本估计总体等知识，解题的关键是能够从统计图中整理出进一步解题的有关信息．22．如图 1，给定锐角三角形ABC ，小明希望画正方形 DEFG ，使 D， E 位于边 BC 上，F， G 分别位于边 AC ， AB 上，他发现直接画图比较困难，于是他先画了一个正方形HIJK ，是的 H， I ，位于射线 BC 上， K 位于射线 BA 上，而不需要求 J 必须位于 AC上．这是他发现可以将正方形HIJK 通过放大或缩小得到满足要求的正方形DEFG ．阅读以上材料，回答小明接下来研究的以下问题：（1）如图 2，给定锐角三角形ABC ，画出所有长宽比为2： 1 的长方形 DEFG ，使 D ， E 位于边 BC 上， F， G 分别位于边 AC ， AB 上．（2）已知三角形 ABC 的面积为 36， BC=12 ，在第（ 1）问的条件下，求长方形DEFG 的面积．【考点】位似变换．【分析】（1）如图 2，先画长方形 HIJK ，使得 HI=2HK ，并且 H ， I 位于射线 BC 上， K 位于射线 BA 上，连结 BJ 并延长交 AC 于点 F，再将长方形 HIJK 通过放大可得到满足要求的长方形DEFG ；如备用图，先画长方形HIJK ，使得 HK=2HI ，并且 H ， I 位于射线BC 上， K 位于射线BA 上，连结BJ 并延长交AC 于点 F，再将长方形HIJK 通过放大可得到满足要求的长方形DEFG ；（2）作△ABC 的高 AM ，交 GF 于 N ．由三角形ABC 的面积为36，求出 AM=6 ．再设AN=x ，由 GF∥BC ，得出△ AGF ∽△ ABC ，根据相似三角形对应高的比等于相似比列出比例式 = ，由此求出 x 的值，进而求解即可．【解答】解：（ 1）如图 2 与备用图1，长方形DEFG 即为所求作的图形；（2）在长方形 DEFG 中，如果 DE=2DG ，如备用图 2，作△ ABC 的高 AM ，交 GF 于 N ．∵三角形 ABC 的面积 = BC ?AM= ×12AM=36 ，∴A M=6 ．设AN=x ，则 MN=6 ﹣ x， DG=MN=6 ﹣x， DE=GF=2 （ 6﹣x） =12﹣2x．∵GF∥ BC ，∴△ AGF ∽△ ABC ，∴= ，∴= ，解得 x=3 ，∴D G=6 ﹣ x=3， DE=2DG=6 ，∴长方形 DEFG 的面积 =6×3=18；在长方形 DEFG 中，如果 DG=2DE ，同理求出 x= ，∴DG=6 ﹣ x=，DE= DG= ，∴长方形 DEFG 的面积 =× =．故长方形 DEFG 的面积为 18 或．【点评】 本题考查了位似变换，相似三角形的判定与性质，根据题意作出符合要求的长方形 DEFG 是解题的关键．五、解答题（本题共 22 分，第 23 题 7 分，第 24 题 7 分，第 25 题 8 分）23．已知关于 x 的二次函数 y 1=x 2﹣（ m+3） x+m+2 ， y 2=﹣ x 2 +bx+c ．（1）求证：方程 x 2﹣（ m+3 ） x+m+2=0 必有实根； （2）若 m 为整数， y 1 的图象与 x 轴有一个交点的横坐标a 满足 5＜ a ＜ 7，求 m 的值； （3）在第（ 2）问的条件下，小明利用函数图象解关于 x 的不等式 y 1 ＜y 2，正确解得该不等式的解集为 3＜ x ＜ 4，求 y 2 的解析式．【考点】 二次函数与不等式（组）；抛物线与 x 轴的交点．【分析】 （1）利用根的判别式即可得出结论；（2）根据 y 1 的图象与 x 轴有一个交点的横坐标 a 满足 5＜a ＜ 7 可知当 x=5 时， y 1＜ 0，当x=7 时， y 1 ＞0 求出 m 的取值范围，再由 m 为整数即可求出 m 的值； （3）先求出当 x=3 ，x=4 时 y 1 的值，再由 y 2 也经过此点即可得出结论． 【解答】 解：（221）∵△ =[ ﹣（ m+3）] ﹣ 4（ m+2） =（ m+1） ≥0，∴方程 x 2﹣（ m+3） x+m+2=0 必有实根； （2）∵ y 1 的图象与 x 轴有一个交点的横坐标 a 满足 5＜ a ＜ 7，且抛物线开口向上，∴f （5）＜ 0， f （7）＞ 0，∴，解得 3＜ m ＜ 5．∵m 为整数， ∴ m =4 ；（3）∵由（ 2）知， m=4，22∴关于 x 的二次函数 y 1=x ﹣（ m+3） x+m+2 可化为 y 1=x ﹣ 7x+6 ，2∵二次函数 y 2=﹣ x + bx+c 经过（ 3，﹣ 6），（ 4，﹣ 6）， ∴，解得，∴y 2 的解析式为 2﹣ 72．y 2=﹣ x +25x【点评】本题考查的是二次函数与不等式组，能根据题意画出图形，利用数形结合求解是解答此题的关键．24．过正方形 ABCD 的顶点 A 任作一条直线 l （ l 不过点 B，C， D），过点 B， C，D 作 l 的垂线段 BF ，CG，DH ．（1）如图 1，若直线 l 过线段 BC 的中点 E，则 BF ： CG： DH=1 ： 1： 2．（2）如图 2，若直线 l 与线段 BC 相交于点 E，则 BF ， CG， DH 满足等量关系式DH=BF+CG ，请证明你的猜想；（3）如果直线l 与线段 CB 的延长线相交，直接写出BF， CG， DH 满足的等量关系式BF=DH+CG ，在直线l 旋转一周的过程中（l 不过点 B ， C， D），直接写出y=的取值范围1＜ y≤2．【考点】四边形综合题．【分析】（1）如图 1 所示：设AB=2a ，根据题意得：BE=a ，由勾股定理可求得AE= a，由面积法可求得 BF 和 HD 的长度，然后再证明△ BFE≌△ CGE，得到BF=CG ，从而可求得答案；（2）如图 2 所示：先根据同角的余角相等，证明∠ADH= ∠ FBE= ∠ GCE，由锐角三角函数的定义可得到，然后利用比例的性质对比例式进行变形可证得：，由 AD=BC ，于是可得到DH=BF+CG ；（3）如图 3 所示：先证明∠ABF= ∠ HDE= ∠ GCE，由锐角三角函数的定义可得到，然后利用比例的性质对比例式进行变形可证得，由 AB=DC 于是得到 BF=DH+CG ；如图 4、 5 所示可求得 BF+CG+DH 的最大值为 2BD ，最小值为 BD ，从而可求得 y 的范围．【解答】解：（ 1）如图 1 所示：连接ED ．设AB=2a ，根据题意得： BE=a ．在 Rt△ ABE 中， AE=，∵，即：，∴BF=．在△ BFE 和△ CGE 中，，∴△ BFE ≌△ CGE．∴BF=CG ．∵，即，∴HD=．∴B F ： CG： DH=1 ：1：2．（2） DH=BF+CG ．理由：如图 2 所示：∵∠ ADH+ ∠ DAH=90 °，∠ BAH+ ∠DAH=90 °，∴∠ ADH= ∠ BAH ．同理∠ FBE= ∠BAH ．∴∠ ADH= ∠ FBE ．∵B F ⊥ AE ， GC⊥AE ，∴BF ∥ GC．∴∠ FBE= ∠ GCE．∴∠ ADH= ∠ FBE= ∠GCE．∴．由可知：，∴，即．∴．∴．∵AD=BC ，∴DH=BF+CG ．（3） BF=DH+CG ．理由：如图 3 所示：根据题意可知：∠ABF= ∠ HDE= ∠ GCE．∴．∴．∴，即．∴．∴．∵AB=DC ，∴BF=DH+CG ．如图 4 所示：当直线经过点 C 时， BF+DH+CG 有最小值，最小值=BD ，∴y=1 ．如图 5 所示：BF+DH+CG 有最大值，最小值=2AC=2BD ，∴y=2 ．∵直线 l 不经过点 B 、C、 D，∴y 的取值范围是：1＜y≤2．。

2019-2020学年北京人大附中九年级（上）月考数学试卷（12月份）副标题题号一二三四总分得分一、选择题（本大题共8小题，共24.0分）1.中国传统扇文化有着深厚的底蕴，下列扇面图形是中心对称图形的是()A. B.C. D.2.方程x2−x=0的解是()A. x=0B. x=1C. x1=0，x2=−1D. x1=0，x2=13.有一个可以自由转动且质地均匀的转盘，被分成6 个大小相同的扇形．在转盘的适当地方涂上灰色，未涂色部分为白色．为了使转动的转盘停止时，指针指向灰色的，则下列各图中涂色方案正确的是()概率为23A. B. C. D.4.下列关于二次函数y=2x2的说法正确的是()A. 它的图象经过点(−1,−2)B. 当x<0时，y随x的增大而减小C. 它的图象的对称轴是直线x=2D. 当x=0时，y有最大值为05.如图，△ABC∽△A′B′C′，AD和A′D′分别是△ABC和△A′B′C′的高，若AD=2，A′D′=3，则△ABC与△A′B′C′的面积的比为()A. 4：9B. 9：4C. 2：3D. 3：26.如图，在平面直角坐标系xOy中，以原点O为位似中心，把线段AB放大后得到线段CD.若点A(1,2)，B(2,0)，D(5,0)，则点A的对应点C的坐标是(),5) C. (3,5) D. (3,6)A. (2,5)B. (527.如图，数轴上有A、B、C三点，点A，C关于点B对称，以原点O为圆心作圆，若点A，B，C分别在⊙O外，⊙O内，⊙O上，则原点O的位置应该在()A. 点A与点B之间靠近A点B. 点A与点B之间靠近B点C. 点B与点C之间靠近B点D. 点B与点C之间靠近C点8.如图，AB是半圆O的直径，按以下步骤作图：(1)分别以A，B为圆心，大于AO长为半径作弧，两弧交于点P，连接OP与半圆交于点C；AC长为半径作弧，两(2)分别以A，C为圆心，大于12弧交于点Q，连接OQ与半圆交于点D；(3)连接AD，BD，BC，BD与OC交于点E．根据以上作图过程及所作图形，下列结论：①BD平分∠ABC；②BC//OD；③CE=OE；④AD2=OD⋅CE；所有正确结论的序号是()A. ①②B. ①④C. ②③D. ①②④二、填空题（本大题共8小题，共24.0分）9.如图，△ABC中，点D，E分别在AB，AC边上，DE//BC，若10.如图，点A、B、C、D、O都在方格纸上，若△COD是由△AOB绕点O按逆时针方向旋转而得，则旋转的角度为______．11.已知反比例函数y=m−2x，当x>0时，y随x增大而减小，则m的取值范围是______．12.若一个扇形的半径为3，圆心角是120°，则它的面积是______．13.小宇调查了初一年级三个班学生的身高，并进行了统计，列出如频数分布表：若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示，不考虑其他因素的影响，则______(填“1班”，“2班”或“3班”)的可供挑选的空间最大．身高/厘米频数班级150≤x<155155≤x<160160≤x<165165≤x<170170≤x<175合计1班181214540 2班1015103240 3班51010874014.如图，在平面直角坐标系xOy中，函数y=2x(x>0)的图象经过点A，B，AC⊥x轴于点C，BD⊥y轴于点D，连接OA，OB，则△OAC与△OBD的面积之和为______．15.为测量附中国旗杆的高度，小宇的测量方法如下：如图，将直角三角形硬纸板△DEF的斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上．测得DE=0.5米，EF=0.25米，目测点D到地面的距离DG=1.6米，到旗杆的水平距离DC=18米，按此方法，可计算出旗杆的高度为______米．16.如图，在Rt△ABC中，∠C=90°，记x=AC，y=BC−AC，在平面直角坐标系xOy中，定义(x,y)为这个直角三角形的坐标，Rt△ABC为点(x,y)对应的直角三角形．有下列结论：①在x轴正半轴上的任意点(x,y)对应的直角三角形均满足AB=√2BC；(x>0)的图象上存在两点边P，Q，使得它们对应的直角三角形②在函数y=2019x相似；③对于函y=(x−2020)2−1(x>0)的图象上的任意一点P，都存在该函数图象上的另一点Q，使得这两个点对应的直角三角形相似；④在函数y=−2x+2020(x>0)的图象上存在无数对点P，Q(P与Q不重合)，使得它们对应的直角三角形全等．所有正确结论的序号是______．三、计算题（本大题共1小题，共6.0分）17.如图，⊙O是△ABC的外接圆，直径BD与AC交于点E，过点D作⊙O的切线，与BC的延长线交于点F．(1)求证：∠F=∠BAC；(2)若DF//AC，若AB=8，CF=2，求AC的长．四、解答题（本大题共11小题，共88.0分）18.解方程：x2−2x=2(x+1)．19.如图，已知∠B=∠C=90°，点E在BC上，且满足AB=4，BE=2，CE=6，CD=3，求证：AE⊥DE．20.已知二次函数y=x2−4x+3．(1)用配方法将y=x2−4x+3化成y=a(x−ℎ)2+k的形式；(2)在平面直角坐标系xOy中画出该函数的图象；(3)当0≤x≤3时，y的取值范围是______．21.如图，四边形ABCD内接于⊙O，OC=2，AC=2√2(1)求点O到AC的距离；(2)求∠ADC的度数．22.某市计划建设一项水利工程，运输公司接到任务后，计划每天运输土方2000m3，共计50天运完，但由于受到各种因素的影响，实际平均每天运输土方vm3，共计t 天运输完成．(1)请直接写出v关于t的函数关系式；(2)为了给后续工程节省出时间，这批土方需要在40天内运输完成，求实际平均每天至少需要比原计划增加多少土方运输量？x2+bx+c=023.已知关于x的一元二次方程14(1)c=2b−1时，求证：方程一定有两个实数根．(2)有甲、乙两个不透明的布袋，甲袋中装有3个除数字外完全相同的小球，分别标有数字1，2，3，乙袋中装有4个除数字外完全相同的小球，分别标有数字1，2，3，4，从甲袋中随机抽取一个小球，记录标有的数字为b，从乙袋中随机抽取一个小球，记录标有的数字为c，利用列表法或者树状图，x2+bx+c=0两个相等的实数根的概率．求b、c的值使方程14(x>0)的24.如图，在平面直角坐标系xOy中，直线l：y=kx−1(k≠0)与函数y=mx 图象交于点A(3,2)．(1)求k，m的值；(2)将直线l沿y轴向上平移t(t>0)个单位后，所得直线与x轴，y轴分别交于点P，(x>0)的图象交于点C．Q，与函数y=mx①当t=2时，求线段QC的长．<3，结合函数图象，直接写出t的取值范围．②若2<QCPQ25.如图，在弧AB和弦AB所组成的图形中，P是弦AB上一动点，过点P作弦AB的垂线，交弧AB于点C，连接AC.已知AB=6cm，设A，P两点间的距离为xcm，P，C两点间的距离为y1cm，A，C两点间的距离为y2cm．小宇根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小宇的探究过程，请补充完整：(1)按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值：x/cmx/cm0123456y1/cm0 2.24 2.83 3.00 2.83 2.240y2/cm0 2.45 3.46 4.24______ 5.486(2)在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点(x,y1)，(x,y2)，并画出函数y1，y2的图象；(3)结合函数图象，解决问题：当△APC有一个角是60°时，AP的长度约为______26.在平面直角坐标系xOy中，抛物线y=x2−2ax+a2−a+4的顶点为A，点B，C为直线y=3上的两个动点(点B在点C的左侧)，且BC=3．(1)求点A的坐标(用含a的代数式表示)；(2)若△ABC是以BC为直角边的等腰直角三角形，求抛物线的解析式；(3)过点A作x轴的垂线，交直线y=3于点D，点D恰好是线段BC三等分点且满足BC=3BD，若抛物线与线段BC只有一个公共点，结合函数的图象，直接写出a 的取值范围．27.如图，在Rt△ABC中，∠ACB=90°，点C关于直线AB的对称点为D，连接BD，CD，过点B作BE//AC交直线AD于点E．(1)依题意补全图形；(2)找出一个图中与△CDB相似的三角形，并证明；(3)延长BD交直线AC于点F，过点F作FH//AE交直线BE于点H，请补全图形，猜想BC，CF，BH之间的数量关系并证明．28.新定义：在平面直角坐标系xOy中，若几何图形G与⊙A有公共点，则称几何图形G的叫⊙A的关联图形，特别地，若⊙A的关联图形G为直线，则称该直线为⊙A 的关联直线．如图，∠M为⊙A的关联图形，直线l为⊙A的关联直线．(1)已知⊙O是以原点为圆心，2为半径的圆，下列图形：①直线y=2x+2；②直线y=−x+3；③双曲线y=2，是⊙O的关联图形的是x______(请直接写出正确的序号)．(2)如图1，⊙T的圆心为T(1,0)，半径为1，直线l：y=−x+b与x轴交于点N，若直线l是⊙T的关联直线，求点N的横坐标的取值范围．(3)如图2，已知点B(0,2)，C(2,0)，D(0,−2)，⊙I经过点C，⊙I的关联直线HB经过点B，与⊙I的一个交点为P；⊙I的关联直线HD经过点D，与⊙I的一个交点为Q；直线HB，HD交于点H，若线段PQ在直线x=6上且恰为⊙I的直径，请直接写出点H横坐标h的取值范围．答案和解析1.【答案】C【解析】解：A、不是中心对称图形，故此选项错误；B、不是中心对称图形，故此选项错误；C、是中心对称图形，故此选项正确；D、不是中心对称图形，故此选项错误；故选：C．根据中心对称图形的概念求解．此题主要考查了中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180度后两部分重合．2.【答案】D【解析】解：x(x−1)=0，x=0或x−1=0，所以x1=0，x2=1．故选：D．先把方程左边分解，这样把原方程化为x=0或x−1=0，然后解一次方程即可．本题考查了解一元二次方程−因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了(数学转化思想)．3.【答案】C，故选项错误；【解析】解：A、指针指向灰色的概率为2÷6=13B、指针指向灰色的概率为3÷6=1，故选项错误；2C、指针指向灰色的概率为4÷6=2，故选项正确；3D、指针指向灰色的概率为5÷6=5，故选项错误．6故选：C．指针指向灰色区域的概率就是灰色区域的面积与总面积的比值，计算面积比即可．本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件(A)；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件(A)发生的概率．4.【答案】B【解析】解：二次函数y =2x 2，当x =−1时，y =2，故它的图象不经过点(−1,−2)，故A 选项不合题意；当x <0时，y 随x 的增大而减小，故选项B 正确； 它的图象的对称轴是直线 y 轴，故C 选项不合题意； 当x =0时，y 有最小值为0，故D 选项不合题意； 故选：B ．直接利用二次函数的性质分别判断得出答案．此题主要考查了二次函数的性质，正确掌握二次函数的增减性是解题关键．5.【答案】A【解析】解：∵△ABC∽△A′B′C′，AD 和A′D′分别是△ABC 和△A′B′C′的高，AD =2，A′D′=3，∴ABA′B′=ADA′D′=23，∴△ABC 与△A′B′C′的面积的比=(23)2=49， 故选：A ．根据相似三角形对应高的比等于相似比求出相似比，根据相似三角形面积的比等于相似比的平方解答．本题考查的是相似三角形的性质，相似三角形面积的比等于相似比的平方、相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．6.【答案】B【解析】 【分析】此题主要考查了位似变换，正确得出对应点的关系是解题关键．在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或−k.利用位似图形的性质得出位似比，进而得出对应点坐标的关系．【解答】解：∵以原点O为位似中心，把线段AB放大后得到线段CD，且B(2,0)，D(5,0)，∴OBOD =25，∵A(1,2)，∴C(52,5)．故选B．7.【答案】C【解析】解：如图，观察图象可知，原点O的位置应该在点B与点C之间靠近B点，故选：C．画出图象，利用图象法即可解决问题；本题考查点与圆的位置关系，解题的关键是理解题意，学会利用图象法解决问题．8.【答案】D【解析】解：由作图可知，OP垂直平分线段AB，OQ平分∠AOC，故①正确，∴OP⊥AB，∴∠AOC=∠BOC=90°，∴∠AOD=12∠AOC=45°，∵OB=OC，∴∠OBC=45°，∴∠AOD=∠OBC=45°，∴OD//BC，故②正确，∴ODBC =OEEC<1，∴OE<EC，故③错误，连接CD．∵∠DCE=∠DCO，∠CDE=∠COD=45°，∴△DCE∽△OCD，∴CDOC =CECD，∴CD2=OD⋅CE，∵∠AOD=∠DOC，∴AD⏜=CD⏜，∴AD=CD，∴AD2=OD⋅CE，故④正确，故选：D．由作图可知，OP垂直平分线段AB，OQ平分∠AOC，利用平行线的判定，相似三角形的性质一一判断即可．本题考查相似三角形的判定和性质，圆周角定理，平行线的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．9.【答案】2.5【解析】解：∵DE//BC，∴△ADE∽△ABC，∴DE：BC=AD：AB，∵AD=2，DB=3，∴AB=AD+BD=5，∴1：BC=2：5，∴BC=2.5，故答案为：2.5．首先由DE//BC，可证得△ADE∽△ABC，进而可根据相似三角形得到的比例线段求得BC的长．本题考查了相似三角形的性质和判定，关键是求出相似后得出比例式，题目比较典型，难度适中．10.【答案】135°【解析】解：∵△COD是由△AOB绕点O按逆时针方向旋转而得，∴∠AOC为旋转角，∵∠AOB=45°，∴∠AOC=135°，即旋转角为135°．故答案为：135°．利用旋转的性质得到∠AOC为旋转角，然后利用∠AOB=45°得到∠AOC的度数即可．本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．11.【答案】m>2【解析】【分析】本题考查了反比例函数的性质，根据反比例函数的性质找出m−2>0是解题的关键．，当x>0时，y随x增大而减小，可得出m−2>0，解之即可根据反比例函数y=m−2x得出m的取值范围．【解答】，当x>0时，y随x增大而减小，解：∵反比例函数y=m−2x∴m−2>0，解得：m>2．故答案为m>2．12.【答案】3π=3π，【解析】解：扇形的面积=120⋅⋅π⋅32360故答案为3π．利用扇形的面积公式计算即可．．本题考查扇形的面积，解题的关键是记住扇形的面积公式S=nπr236013.【答案】1班【解析】解：身高在160cm和170cm之间同学人数：一班26人，二班13人，三班18人，因此可挑选空间最大的是一班，故答案为：1班．根据各个班身高在160cm和170cm之间同学的人数，进行判断即可．考查频数分布表的表示方法，从表格中获取数据和数据之间的关系是正确判断的前提．14.【答案】2【解析】解：∵函数y=2x(x>0)的图象经过点A，B，AC⊥x轴于点C，BD⊥y轴于点D，∴S△OAC=S△OBD=12×2=1，∴S△OAC+S△OBD=1+1=2．故答案为2．根据反比例函数比例系数k的几何意义可得S△OAC=S△OBD=12×2=1，再相加即可．本题考查了反比例函数比例系数k的几何意义：过反比例函数图象上的点向x轴或y轴作垂线，这一点和垂足、原点组成的三角形的面积等于12|k|．15.【答案】10.6【解析】解：∵CD⊥AB，△DEF为直角三角形，∴∠DEF=∠ACD，∵∠ADC=∠FDE，∴△ACD∽△FED，∴DECD =EFAC，∵DE=0.5米，EF=0.25米，DC=18米，∴0.518=0.25AC，∴AC=9米，∵DG=1.6米，∴BC=1.6米，∴AB=10.6米，故答案为：10.6．根据题意证出△ACD∽△FED，进而利用相似三角形的性质得出AC的长，即可得出答案．此题主要考查了相似三角形的应用；由三角形相似得出对应边成比例是解题关键．16.【答案】①③④【解析】解：①∵在x轴正半轴上的任意点(x,y)，∴y=0，∴AC=BC，∴AB=√2BC；②设P({x1,2019 x1)，Q(x2,2019x2)，则对应的直角三角形的直角边分别为x1，x1+2019 x1；x2，x2+2019x2，若两个三角形相似，则有x1x1+2019x1=x2x2+2019x2，∴x22=x12，∵x>0，∴x1=x2，∴不存在两点边P，Q，使得它们对应的直角三角形相似；③设P(x1,(x1−2020)2−1)，Q(x2,(x2−2020)2−1)，则对应的直角三角形的直角边分别为x1+(x1−2020)2−1，x1；x2，x2+(x2−2020)2−1，若两个三角形相似，则有x1(x1−2020)2−1=x2(x2−2020)2−1，∴(x1−x2)(x1x2+1−20202)=0，∵x>0，∴x1x2+1=20202，∴图象上的任意一点P，都存在该函数图象上的另一点Q，使得这两个点对应的直角三角形相似；④设P(x1,−2x1+2020)，Q(x2,−2x2+2020)，则对应的直角三角形的直角边分别为x1，−x1+2020；x2，−x2+2020，若两个三角形全等，则有x1=−x2+2020，x2=−x1+2020，∴x2+x1=2020，∵x>0，∴图象上存在无数对点P，Q，使得它们对应的直角三角形全等；故答案为①③④．①在x轴正半轴上的任意点(x,y)，则y=0，所以AC=BC，由勾股定理可得AB=√2BC；②设P({x1,2019 x1)，Q(x2,2019x2)，则对应的直角三角形的直角边分别为x1，x1+2019 x1；x2，x2+2019x2，若两个三角形相似，则有x1x1+2019x1=x2x2+2019x2，可得x22=x12，当x>0时x1=x2；③设P(x1,(x1−2020)2−1)，Q(x2,(x2−2020)2−1)，则对应的直角三角形的直角边分别为x1+(x1−2020)2−1，x1；x2，x2+(x2−2020)2−1，若两个三角形相似，则有x1(x1−2020)2−1=x2(x2−2020)2−1，(x1−x2)(x1x2+1−20202)=0，由条件可得x1x2+1=20202；④设P(x1,−2x1+2020)，Q(x2,−2x2+2020)，则对应的直角三角形的直角边分别为x1，−x1+2020；x2，−x2+2020，若两个三角形全等，则有x1=−x2+2020，可得x2+x1=2020．本题考查函数的性质，新定义，三角形性质；能够理解题意，将问题转化为直角三角形相似与全等，利用相似与全等的关系结合直角三角形的性列出正确的等式，再能正确求解方程是解题的关键．17.【答案】(1)证明：∵DF是⊙O的切线，∴OD⊥DF，∴∠ODF=90°，∴∠F+∠DBC=90°，∵BD是⊙O的直径，∴∠BAD=90°，∴∠BAC+∠DAC=90°，∵∠DBC=∠DAC，∴∠BAC=∠F(2)解：连接CD，∵DF//AC，∠ODF=90°，∴∠BEC=∠ODF=90°，∴直径BD⊥AC于E，∴AE=CE=12AC，∴AB=BC，∵AB=8，∴BC=8，∵BD是⊙O的直径，∴∠BCD=90°，∴∠DBC+∠BDC=90°，∵∠DBC+∠F=90°，∴∠BDC=∠F，∵∠BCD=∠FCD=90°，∴△BCD∽△DCF，∴BCDC =DCCF，∵BC=8，CF=2，∴DC=4，∴BD=√BC2+CD2=4√5．∵在△BCD中，S△BCD=12BC⋅CD=12BD⋅CE，∴CE=85√5，∴AC=2CE=165√5．【解析】(1)证∠F+∠DBC=90°，可得∠BAC+∠DAC=90°，又∠DBC=∠DAC，则∠BAC=∠F，结论得证；(2)连接CD，证明△BCD∽△DCF，可得BCDC =DCCF，求出DC=4，BD=4√5，由三角形面积可得出CE，则AC可求出．本题考查了相似三角形的性质及判定，切线的性质，等腰三角形的判定与性质，勾股定理，三角形的面积等知识，解答时运用好切线的性质求解是解答本题的关键．18.【答案】解：整理得x2−4x=2，x2−4x+4=2+4，即(x−2)2=6，∴x−2=±√6，∴x1=2+√6，x2=2−√6．【解析】整理得x2−4x=2，然后利用配方法求解即可．本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．19.【答案】证明：∵AB=4，BE=2，CE=6，CD=3，∴ABCE =BECD，∵∠B=∠C=90°，∴△ABE∽△ECD，∴∠A=∠CED，∵∠B=90°，∴∠A+∠AEB=90°，∴∠CED+∠AEB=90°，∴∠AED=180°−∠AEB−∠CED=90°，∴AE⊥DE．【解析】证明△ABE∽△ECD，可得∠A=∠CED，则∠CED+∠AEB=90°，可得出∠AED= 180°−∠AEB−∠CED=90°，则结论得证．本题考查的是相似三角形的判定与性质，熟知相似三角形的性质是解答此题的关键．20.【答案】(1)y=x2−4x+3=(x−2)2−1；(2)这个二次函数的图象如图：(3)−1≤y≤3【解析】解：(1)见答案；(2)见答案；(3)当0≤x≤3时，−1≤y≤3．故答案为−1≤y≤3．【分析】(1)运用配方法把一般式化为顶点式；(2)根据函数图象的画法画出二次函数图象即可；(3)运用数形结合思想解答即可．本题考查的是二次函数的三种形式、二次函数的性质，掌握配方法把一般式化为顶点式是解题的关键．21.【答案】解：(1)连接OA，作OH⊥AC于H，OA2+OC2=8，AC2=8，∴OA2+OC2=AC2，∴△AOC为等腰直角三角形，∴OH=12AC=√2，即点O到AC的距离为√2；(2)由圆周角定理得，∠B=12∠AOC=45°，∵四边形ABCD内接于⊙O，∴∠ADC=180°−45°=135°．【解析】(1)连接OA，作OH⊥AC于H，根据勾股定理的逆定理得到∠AOC=90°，根据等腰直角三角形的性质解答；(2)根据圆周角定理求出∠B，根据圆内接四边形的性质计算，得到答案．本题考查度数圆内接四边形的性质、圆周角定理、勾股定理的逆定理，掌握圆内接四边形对角互补是解题的关键．22.【答案】解：(1)由题意得：v=2000×50t =100000t；(2)当t=40时，v=10000040=2500，2500−2000=500(m3)，答：实际平均每天至少需要比原计划增加500m3土方运输量．【解析】(1)根据题意得等量关系：平均每天运输土方=土方总量÷时间，然后可得v关于t的函数关系式；(2)求出当t=40时v的值，然后其计算与2000的差即可．此题主要考查了反比例函数的应用，关键是正确理解题意，找出题目中的等量关系．23.【答案】(1)证明：∵△=b2−4⋅14c=b2−c=0，∴将c=2b−1代入得：△=b2−(2b−1)=b2−2b+1=(b−1)2≥0，∴方程一定有两个实数根；(2)解：画树状图得：∵共有12种等可能的结果，若方程有两个相等的实数根，△=b2−4⋅14c=b2−c=0，∴b2=c，满足条件的结果有(1,1)和(2,4)，共2种，∴P(b、c的值使方程14x2+bx+c=0两个相等的实数根的概率)=16．【解析】(1)直接利用根的判别式以及完全平方公式进而分析得出答案；(2)首先根据题意画出树状图，然后由树状图求得所有等可能的结果；可得2x+y=6的情况，再利用概率公式求解即可求得答案．此题考查的是用列表法或树状图法求概率．注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．24.【答案】解：(1)将点A(3,2)的坐标分别代入y=kx−1(k≠0)与y=mx(x>0)中，得2=3k−1，2=m3，∴k=1，m=6；(2)①∵直线y=kx−1与y轴交于点(0,−1)，∴当t=2时，Q(0,1)．此时直线解析式为y=x+1，代入函数y=6x中，整理得，x(x+1)=6，解得x1=−3(舍去)，x2=2，∴C(2,3)，∴QC=√(2−0)2+(3−1)2=2√2．②如图，作CD⊥x轴于D，若QCPQ =2时，则ODOP=2，CDOQ=3，∵直线解析式系数k=1，∴OP=OQ，设OP=OQ=a，∴OD=2a，CD=3a，∴CD=62a =3a，∴3a=3a，解得a=1，∴此时t=1+1=2，若QCPQ =3时，则ODOP=3，CDOQ=4，∵直线解析式系数k=1，∴OP=OQ，设OP=OQ=a，∴OD=3a，CD=4a，∴CD=63a =2a，∴4a=2a，解得a=√22，∴此时t=1+√22，∴若2<QCPQ <3，结合函数图象，得出t的取值范围是1+√22<t<2．【解析】(1)将点A分别代入y=kx−1(k≠0)与y=mx(x>0)，即可求出k、m的值；(2)①求出当t=2时直线解析式，代入函数y=6x中，整理得，x(x+1)=6，解方程求出点C的坐标，即可求出QC的长；②观察图象解答即可．本题考查了一次函数与反比例函数的交点问题，待定系数法求解析式，利用函数图象性质解决问题是本题的关键．25.【答案】4.90 1.50或4.50【解析】解：(1)利用测量法可知：当x=4时，y2=4.90．故答案为4.90．(2)函数图象如图所示：(3)函数y1与直线y=√3x的交点的横坐标为1.50，x的交点的横坐标为4.50，函数y1与直线y=√33故当△APC有一个角是60°时，AP的长度约为1.50或4.50．故答案为1.50或4.50．(1)利用测量法解决问题即可．(2)利用描点画出函数图象即可．(3)利用图象法求出函数y1与直线y=√3x，直线y=√3x的交点的横坐标即可解决问题．3本题属于圆综合题，考查了解直角三角形，勾股定理，一次函数的性质，函数的图象与性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．26.【答案】解：(1)y=x2−2ax+a2−a+4=(x−a)2+4−a，故点A(a,4−a)；(2)点A所在的直线为：y=4−x，联立y=4−x与y=−x并解得：x=1，故两个直线的交点为(1,3)；①当点C的坐标为：(1,3)时，则点B(−2,3)，点A(−2,6)，a=−2，故抛物线的表达式为：y=(x+2)2+6；②当点B的坐标为：(1,3)时，则点A(4,0)，则a=4，故抛物线的表达式为：y=(x−4)2；综上，抛物线的表达式为：y=(x+2)2+6或y=(x−4)2；(3)点A(a,4−a)，则点D(a,3)，BC=3BD，则点B、C的坐标分别为：(a−1,3)、(a+2,3)，将抛物线y=x2−2ax+a2−a+4与直线y=3联立并解得：x=a±√a−1，故点E、F的坐标分别为：(a−√a−1,3)、(a+√a−1,3)，①当a=1时，点E、B、C、F的坐标分别为：(1,3)、(0,3)、(2,3)、(1,3)，而点A(1,3)，此时，抛物线于BC只有一个公共点；②当a>1时，当点C、F重合时，则a+√a−1=a+2，解得：a=5；当点B、E重合时，a−√a−1=a−1，解得：a=2，故2<a≤5；综上，a=1或2<a≤5．【解析】(1)y=x2−2ax+a2−a+4=(x−a)2+4−a，即可求解；(2)分当点C的坐标为：(1,3)时、点B的坐标为：(1,3)时，两种情况分别求解；(3)分a=1、a>1两种情况，分别求解即可．本题考查的是二次函数综合运用，涉及到一次函数的性质、等腰直角三角形的性质等，其中(2)、(3)，都要注意分类求解，避免遗漏．27.【答案】解：(1)如图1所示：(2)与△CDB相似的三角形是△ABE，理由如下：∵点C关于直线AB的对称点为D，∴CH=DH，AB⊥CD，∴AB是CD的垂直平分线，∴AD=AC，BC=BD，且AB⊥CD，∴∠ACD=∠ADC，∠CAB=∠DAB，∠BCD=∠BDC，∠DBA=∠CBA，∵∠ACB=90°，∴∠ABC+∠CAB=90°，且∠ABC+∠BCH=90°，∠BAC+∠ACD=90°，∴∠BCD=∠BAC，∠ACD=∠ABC，∴∠DAB=∠BCD=∠BAC=∠BDC，∵AC//BE，∴∠CAB=∠ABE，∴∠CDB=∠ABE，且∠DAB=∠BCD，∴△BCD∽△EAB；(3)BH⋅FC=BC2+CF2，理由如下：如图2，∵∠ACB=90°，∴BC2+CF2=BF2，∵△BCD∽△EAB，∴∠AEB=∠CBD，∵AE//FH，∴∠H=∠AEB=∠CBD，∵AC//BE，∴∠CFB=∠FBH，∴△FCB∽△BFH，∴BHBF =BFFC，∴BF2=BH⋅FC，∴BH⋅FC=BC2+CF2．【解析】(1)由题意补全图形；(2)由轴对称的性质可得AB是CD的垂直平分线，可得AD=AC，BC=BD，由等腰三角形的性质和余角的性质，可得∠DAB=∠BCD=∠BAC=∠BDC，由平行线的性质可得∠CAB=∠ABE=∠CDB，可证△BCD∽△BAE；(3)由勾股定理可得BC2+CF2=BF2，通过证明△FCB∽△BFH，可得BHBF =BFFC，可得结论．本题是几何变换综合题，考查了轴对称的性质，线段垂直平分线的性质，等腰三角形的性质，相似三角形的判定和性质，找到正确的相似三角形是本题的关键．28.【答案】①③【解析】解：(1)由题意①③是⊙O的关联图形，故答案为①③．(2)如图1中，∵直线l1y=−x+b是⊙T的关联直线，∴直线l的临界状态是和⊙T相切的两条直线l1和l2，当临界状态为l1时，连接TM(M为切点)，∴TM=1，TM⊥MB，且∠MNO=45°，∴△TMN是等腰直角三角形，∴TN=√2，OT=1，∴N(1+√2,0)，把N(1+√2,0)代入y=−x+b中，得到b=1+√2，同法可得当直线l2是临界状态时，b=−√2+1，∴点N的横坐标的取值范围为−√2+1≤≤√2+1．(3)如图3−1中，当点Q在点P是上方时，连接BQ，PD交于点H，当圆心I在x轴上时，点H与点C重合，此时H(2,0)，得到h的最大值为2，如图3−2中，当点P在点Q是上方时，连接BQ，PD交于点H，当圆心I在x轴上时，点H(−6,0)得到h的最小值为−6，综上所述，−6≤ℎ<0，0<ℎ≤2．(1)根据⊙A的关联图形的定义判断即可．(2)直线l的临界状态是和⊙T相切的两条直线l1和l2，求出两种特殊情形的点N的横坐标即可解决问题．(3)分两种情形：如图3−1中，当点Q在点P是上方时，连接BQ，PD交于点H，当圆心I在x轴上时，点H与点C重合，此时H(2,0)，得到h的最大值为2.如图3−2中，当点P在点Q是上方时，连接BQ，PD交于点H，当圆心I在x轴上时，点H(−6,0)得到h的最小值为−6，由此即可解决问题．本题属于圆综合题，考查了⊙A的关联图形的定义，直线与圆的位置关系等知识，解题的关键是理解题意，学会寻找特殊点，特殊位置解决问题，属于中考压轴题．。