2019届人大附中12月月考试题理科试题(答案)
- 格式:docx
- 大小:574.37 KB
- 文档页数:9

2019届高三12月月考理综物理试题二、选择题1. 一平行板电容器两极板之何充满云母介质,接在恒压直流电源上,若将云母介质移出,则电容器A. 极板上的电荷量变大,极板间的电场强度变大B. 极板上的电荷量变小,极板间的电场强度变大C. 极板上的电荷量变大,极板间的电场强度不变D. 极板上的电荷量变小,极板间的电场强度不变【答案】D【解析】试题分析:电容器接在恒压直流电源上,则电容器两端的电势差不变,将云母介质移出后,介电常数减小,根据电容的决定式知,介电常数减小,电容减小,由于电压不变,根据可知,电荷量Q减小,由于电容器的电压不变,板间的距离d不变,根据可知,极板间的电场强度不变,所以ABC错误,D正确。
考点:电容器的动态分析【名师点睛】本题是电容器的动态分析问题,关键抓住不变量,当电容器与电源始终相连,则电势差不变;当电容器与电源断开,则电荷量不变.要掌握、、三个公式。
视频2. 铁路在弯道处的内外轨道高度不同,已知内外轨道平面与水平的夹角为,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于,则()A. 内轨对内侧车轮轮缘有挤压B. 外轨对外侧车轮轮缘有挤压C. 这时铁轨对火车的支持力等于D. 这时铁轨对火车的支持力等于【答案】C【解析】火车的重力和轨道对火车的支持力的合力恰好等于需要的向心力时有:,解得:,此时车轮轮缘对内、外均无压力,故A B错误;当内外轨没有挤压力时,受重力和支持力,可得支持力,故C正确,D错误。
所以C正确,ABD错误。
3. 如图所示,空间有两个等量的异种点电荷M、N固定在水平面上,虚线POQ为MN连线的中垂线,一负的试探电荷在电场力的作用下从P点运动到Q点,其轨迹为图中的实线,轨迹与MN连线的交点为A。
则下列叙述正确的是A. 电势B. 电势C. 电场强度D. 电场强度【答案】A【解析】N点的点电荷对负试探电荷是排斥的,所以N点放的是负点电荷,M点放置的是正点电荷,等量异种点电荷电场线如图所示,根据沿电场线方向电势降低以及电场线越密电场强度越大可知,,A正确.4. 如图所示,在圆形区域内,存在垂直纸面向外的匀强磁场,ab是圆的一条直径,一带电粒子从a点射入磁场,速度大小为,方向与ab成时恰好从b点飞出磁场,粒子在磁场中运动的时间为t;若仅将速度大小改为v,则粒子在磁场中运动的时间为(不计带电粒子所受重力)()A. 3tB. tC. tD. 2t【答案】D【解析】试题分析:当粒子的速度为2v时,半径为r1,由题意知,轨迹对应的圆心角为60o,所以运动的时间,当速度为v时,根据得:,故半径,由几何关系知,轨迹的圆心角为120o,故时间,所以ABC错误;D正确。

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……2019高三理综12月月考试题第Ⅰ卷(选择题共126分)本卷共21小题,每小题6分,共126分。
可能用到的相对原子质量:H 1 C 12 N 14、O 16、Mg 24 、Al 27 、Na 23Fe 56 Cu 64 Si28 S32 Cr52一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.当人所处环境温度从25℃降至5℃,耗氧量、尿量、抗利尿激素及体内酶活性的变化依次为A .减少、减少、增加、不变B .增加、增加、减少、不变 ( )C .增加、减少、增加、不变D .增加、增加、减少、降低2.下面的①、②、③分别表示生物体内的三个生理过程,其中Q 分别代表三种物质,下列有关Q 的叙述错误的是A .Q 可能位于细胞膜上B .Q 中可能含有硫元素C .①不一定发生在细胞内D .②必须依赖三磷酸腺苷3.关于下列四图的叙述中,正确的是 ()A .甲图中共有5种核苷酸B .在小鼠的体细胞内检测到的化合物丁很可能是蔗糖C .组成丙物质的单糖是脱氧核糖或核糖D .乙图所示的化合物中不含糖类物质 4.下图所示为来自同一人体的4 种细胞,下列叙述正确的是DNA …—A —T —G —C —… RNA …—U —A —C —G —…甲A —P~P~P乙丙C 12H 22O 11丁A .因为来自同一人体,所以各细胞中的 DNA 含量相同B .因为各细胞中携带的基因不同,所以形态、功能不同C .虽然各细胞大小不同,但细胞中含量最多的化合物相同D .虽然各细胞的生理功能不同,但吸收葡萄糖的方式相同5.下图所示实验能够说明A .效应T 细胞的作用B .浆细胞产生抗体的作用C .病毒刺激淋巴细胞增殖的作用D .病毒抗原诱导B 细胞分化的作用6.下图是人体缩手反射的反射弧结构,方框甲代表大脑皮层、乙代表脊髓神经中枢。

人大附中2019 届高三12 月月考理科综合能力测试试卷物理部分1.如图所示,为某点电荷电场中的一条电场线,其上两点、相距为,电势差为,点的场强大小为,把电荷量为的试探电荷从点移到点,电场力做功为,该试探电荷在点所受的电场力大小为.下列关系正确的是()A. B. C. D.【答案】B【解析】试题分析:a点的场强大小为E,电荷量为q的试探电荷在b点所受的电场力大小为F,因为不一定是匀强电场,故不一定满足,选项A错误;由电场力做功的公式可知W=qU,选项B正确;根据点电荷的场强公式,但是公式中的q应该是场源电荷的电量,d是该点到场源电荷的距离,选项C错误;由于不一定是匀强电场,故不一定满足U=Ed,选项D错误。
考点:电场强度2.如图所示,闭合开关S 后,A 灯与B 灯均发光,当滑动变阻看的滑片P 向左滑动时,以下说法中正确的是()A. A 灯变暗B. B 灯变亮C. 电源的输出功率可能减小D. 电源的总功率可能增大【答案】C【解析】【分析】当P向左端移动时,滑动变阻器连入电路的电阻变大,所以电路的总电阻增大,故电路路端电压增大,电路的总电流减小,根据欧姆定律和有关知识对电路进行动态分析。
【详解】A、当P向左端移动时,滑动变阻器连入电路的电阻变大,所以电路的总电阻增大,故电路路端电压增大,电路的总电流减小,即通过B灯的电流减小,所以B灯两端的电压减小,B等变暗,故B错误;电路路端电压增大,而B两端的电压减小,所以并联电路两端电压增大,所以A灯电流增大,A灯变亮,故A错误。
C、根据电源输出功率公式P=EI-r可得,当外电路中的电阻等于电源内阻时,电源的输出功率最大,因为题中不知道,外电路电阻和电源内阻的关系,所以电源的输出功率可能减小,可能增大,故C正确.D、电源的总功率为P=EI,电流减小,所以电源的总功率减小,故D错误故选:C3.小芳家正在使用的电器有电灯、洗衣机、电冰箱,小芳从家里的总电能表中测得在时间t 内消耗的电能为W。

北京市中国人民大学附属中学 2019届高三下学期理科数学练习卷(一)本试卷共4页,满分150分.考试用时120分钟.注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮搽干净后,再选涂其他答案标号,写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,答在本试题上无效.4.考试结束,将本试题和答题卡一并交回.一、选择题(共8小题,每小题5分,共40分。
)1.设集合{}2|230A x Z x x =∈--<,{}1,0,1,2B =-,则A B =A.{}0,1 B.{}0,1,2 C.{}1,0,1-D.{}1,0-2.已知i 为虚数单位,复数212iz i+=-,则3z = A.iB.i -C.1D.1-3.命题“[]20,2,20x x x ∀∈-≤”的否定是A.[]20,2,20x x x ∀∈-> B.[]20000,2,20x x x ∃∈-≤ C.[]20,2,20x x x ∀∉->D.[]20000,2,20x x x ∃∈->4.()f x 是R 上的奇函数,且2(1),1()log ,01f x x f x x x ->⎧=⎨<≤⎩则3()2f -=A.12 B.12-C.1D.1- 5.已知焦点在x 轴上的双曲线的一条渐近线的倾斜角为6p,且其焦点到渐近线的距离为2,则该双曲线的标准方程为A.22132x y -=B.2213x y -= c.22164x y -= D.221124x y -= 6.两名同学分3本不同的书,其中一人没有分到书,另一人分得3本书的概率为A.12 B.14 C.13 D.167.中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等。

北京人大附中2019届九年级上学期12月月考数学试卷一、选择题(本题共16分,每小题2分)第1-8题有四个选项,符合题意的选项只有一个1.(2分)在Rt△ABC中,∠C=90°,BC=4,AB=5,则sin A的值为()A.B.C.D.2.(2分)二次函数y=(x﹣5)2+7的最小值是()A.﹣7B.7C.﹣5D.53.(2分)如图,DE∥BC,AD:DB=2:3,EC=6,则AE的长是()A.3B.4C.6D.104.(2分)如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°5.(2分)如图,点A在双曲线y=上,B在y轴上,且AO=AB,若△ABO的面积为6,则k的值为()A.6B.﹣6C.12D.﹣126.(2分)北京教育资源丰富,高校林立,下面四个高校校徵主题图案中,既不是中心对称图形,也不是轴对称图形的是()A.北京林业大学B.北京体育大学C.北京大学D.中国人民大学7.(2分)如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为12米,若小明的眼晴与地面的距离为1.5米,则旗杆的高度为()A.9B.12C.14D.188.(2分)根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.下列叙述正确的是()A.运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同B.运动员高强度运动后,最高血乳酸浓度大约为250mg/LC.采用慢跑活动方式放松时,运动员必须慢跑70min后才能基本消除疲芳D.运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用跑活动方式来放松二、填空题(本题共16分,每小题2分)9.(2分)sin A=,则锐角A=度.10.(2分)如图,AB∥CD,AB=CD,线段AD与BC交于点M,△AMB的周长为2,则△CMD的周长为.11.(2分)已知点P(﹣4,y1)和Q(﹣1,y2)在反比例函数y=的图象上,则y1与y2的大小关系为y1 y2(填“>”,“<”或“=”)12.(2分)将抛物线y=x2,沿x轴向左平移1个单位后,得到的物线的解析式是.13.(2分)如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=50°,则∠BAC=.14.(2分)如图,边长为3的正方形OABC的顶点A,C分别在x轴y轴的正半轴上,若反比例数y=的图象与正方形OABC的边有公共点,则k的取值范围是.15.(2分)如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果,那么称线段AB被点C黄金分割.黄金分割经常被应用在建筑雪等艺术领域.如图2,在“附中学子故宫行”活动中,同学们沿着紫禁城的中轴线,从内金水桥走到了太和殿,领略了古代建筑的美轮美奂,太和门位于太和殿于内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割,已知太和殿到内金水桥的距离约为100丈,设太和门到太和殿之间的距离为x丈,要求x,则可列方程为.16.(2分)如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=AD④BE2+CD2=2(AD2+AB2)三、解答题(本题共6分,第17-22题,每小题5分,第236题,每小题5分,第27-题,每小题5分)17.(5分)计算:tan60°﹣4sin30°cos45°18.(5分)如图,在由边长为1个单位的长度的小正方形组成的网格图中,已知点O及△ABC的顶点均为网格线的交点(1)在给定网格中,以O为位似中心,将△ABC放大为原来的三倍,得到请△A'B'C',请画出△A'B'C';(2)B'C'的长度为单位长度,△A′B′C′的面积为平方单位.19.(5分)如图,△ABC中,点D在AB上,∠ACD=∠ABC.(1)求证:△ACD∽△ABC;(2)若AD=2,AB=6,求AC的长.20.(5分)关于x的一元二次方程x2+(2m﹣1)x+m2﹣1=0有两个不相等的实数根(1)求m的取值范围;(2)若m是满足条件的最大整数,求方程的根.21.(5分)在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=2,且其顶点在直线y=﹣2x+2上.(1)直接写出抛物线的顶点坐标;(2)求抛物线的解析式.22.(5分)工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.(1)写出该材料温度上升和下降阶段,y与x的函数关系式:①上升阶段:当0≤x≤5时,y=;②下降阶段:当x>5时,y.(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?23.(6分)如图,AB是⊙O的直径,过点B做⊙O的切线BC,点D为⊙O上一点,且CD=CB,连结DO 并延长交CB的延长线于点E.(1)求证:CD是⊙O的切线;(2)连接AC,若BE=4,DE=8,求线段AC的长.24.(6分)在平面直角坐标系xOy中,反比例数y=的图象过点A(6,1).(1)求反比例数的表达式;(2)过点A的直线与反比例数y=图象的另一个交点为B,与y轴交点交于点P.①若点P为原点,直接写出点B的坐标;②若PA=2PB,求点P的坐标.25.(6分)如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D由点A到点B运动的过程中,设AD=xcm,AE=ycm.小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为cm.26.(6分)在平面直角坐标系xOy中抛物线y=ax2﹣2ax+3(a≠0)的顶点A在第一象限,它的对称轴与x 轴交于点B,△AOB为等腰直角三角形(1)写出抛物线的对称轴为直线;(2)求出抛物线的解析式;(3)垂直于y轴的直线L与该抛物线交于点P(x1,y1),Q(x2,y2)其中x1<x2,直线L与函数y=(x>0)的图象交于点R(x3,y3),若,求x1+x2+x3的取值范围.27.(7分)如图,∠MON=α(0<α<90°),A为OM上一点(不与O重合),点A关于直线ON的对称点为B,AB与ON交于点C,P为直线ON上一点(不与O,C重合)将射线PB绕点P顺时针旋转β角,其中2α+β=180°,所得到的射线与直线OM交于点Q这个问题中,点的位置和角的大小都不确定,在这里我们仅研究两种特殊情况,一般的情况留给同学们深入探索(1)如图1,当α=45°时,此时β=90°,若点P在线段OC的延长线上①依题意补全图形;②求∠PQA﹣∠PBA的值;(2)如图2,当α=60°,点P在线段CO的延长线上时,用等式表示线段OC,OP,AQ之间的数量关系,并证明.28.(7分)对于平面直角坐标系xOy中的⊙C和点P,给出如下定义若在⊙C上存在一点Q,使得△PCQ是以CQ为底边的等腰三角形且底角∠PCQ≤60°,则称点P为⊙C的“邻零点”,(1)当⊙O的半径为2时,①在点P1(﹣2,0),P2(1,﹣1),P3(0,3)中,⊙O的“邻零点”是;②点P在直线y=﹣x上,若P为⊙O的“邻零点”,求点P的横坐标x P的取值范围.(2)⊙C的圆心在x轴上,半径为4,直线y=2x+2与x轴,y轴分别交于点A,B,若线段AB上的点都是⊙C的“邻零点”,直接写出圆心C的横坐标t的取值范围.2018-2019学年北京人大附中九年级(上)月考数学试卷(12月份)参考答案与试题解析一、选择题(本题共16分,每小题2分)第1-8题有四个选项,符合题意的选项只有一个1.(2分)在Rt△ABC中,∠C=90°,BC=4,AB=5,则sin A的值为()A.B.C.D.【分析】直接利用已知画出图形,进而利用锐角三角函数关系得出答案.【解答】解:如图所示:∵∠C=90°,BC=4,AB=5,∴sin A==,故选:C.【点评】此题主要考查了锐角三角函数关系,正确记忆边角关系是解题关键.2.(2分)二次函数y=(x﹣5)2+7的最小值是()A.﹣7B.7C.﹣5D.5【分析】根据二次函数的性质求解.【解答】解:∵y=(x﹣5)2+7∴当x=5时,y有最小值7.故选:B.【点评】本题考查了二次函数的最值:当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=﹣,函数最小值y=;当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=﹣,函数最大值y=.3.(2分)如图,DE∥BC,AD:DB=2:3,EC=6,则AE的长是()A.3B.4C.6D.10【分析】利用平行线分线段成比例定理得到=,然后利用比例的性质可计算出AE的长.【解答】解:∵DE∥BC,∴=,即=,∴AE=4.故选:B.【点评】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了平行线分线段成比例定理.4.(2分)如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°【分析】先根据OA=OC,∠ACO=45°可得出∠OAC=45°,故可得出∠AOC的度数,再由圆周角定理即可得出结论.【解答】解:∵OA=OC,∠ACO=45°,∴∠OAC=45°,∴∠AOC=180°﹣45°﹣45°=90°,∴∠B=∠AOC=45°.故选:D.【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.5.(2分)如图,点A在双曲线y=上,B在y轴上,且AO=AB,若△ABO的面积为6,则k的值为()A.6B.﹣6C.12D.﹣12【分析】过点A作AD⊥y轴于点D,结合等腰三角形的性质得到△ADO的面积为3,所以根据反比例函数系数k的几何意义求得k的值.【解答】解:如图,过点A作AD⊥y轴于点D,∵AB=AO,△ABO的面积为6,=|k|=3,∴S△ADO又反比例函数的图象位于第一、三象限,k>0,则k=6.故选:A.【点评】本题考查反比例函数系数k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.也考查了等腰三角形的性质以及反比例函数图象上点的坐标特征.6.(2分)北京教育资源丰富,高校林立,下面四个高校校徵主题图案中,既不是中心对称图形,也不是轴对称图形的是()A.北京林业大学B.北京体育大学C.北京大学D.中国人民大学【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、是轴对称图形,不是中心对称图形,故本选项错误;B、不是轴对称图形,是中心对称图形,故本选项错误;C、是轴对称图形,不是中心对称图形,故本选项错误;D、既不是中心对称图形,也不是轴对称图形,故本选项正确.故选:D.【点评】本题考查了中心对称及轴对称的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.7.(2分)如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为12米,若小明的眼晴与地面的距离为1.5米,则旗杆的高度为()A.9B.12C.14D.18【分析】如图,BC=2m,CE=12m,AB=1.5m,利用题意得∠ACB=∠DCE,则可判断△ACB∽△DCE,然后利用相似比计算出DE的长.【解答】解:如图,BC=2m,CE=12m,AB=1.5m,由题意得∠ACB=∠DCE,∵∠ABC=∠DEC,∴△ACB∽△DCE,∴,即,∴DE=9.即旗杆的高度为9m.故选:A.【点评】本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,用相似三角形对应边的比相等的性质求物体的高度.8.(2分)根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.下列叙述正确的是()A.运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同B.运动员高强度运动后,最高血乳酸浓度大约为250mg/LC.采用慢跑活动方式放松时,运动员必须慢跑70min后才能基本消除疲芳D.运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用跑活动方式来放松【分析】根据函数图象横纵坐标表示的意义判断即可.【解答】解:A、运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度不同,错误;B、运动员高强度运动后最高血乳酸浓度大约为200mg/L,错误;C、采用慢跑活动方式放松时,运动员必须慢跑40min后才能基本消除疲劳,错误;D、运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用慢跑活动方式来放松,正确;故选:D.【点评】本题考查了函数的图象,解答本题的关键是正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.二、填空题(本题共16分,每小题2分)9.(2分)sin A=,则锐角A=45度.【分析】根据sin45°=解答即可.【解答】解:∵sin45°=,∴锐角A=45°.【点评】此题比较简单,只要熟记特殊角的三角函数值即可.10.(2分)如图,AB∥CD,AB=CD,线段AD与BC交于点M,△AMB的周长为2,则△CMD的周长为6.【分析】根据相似三角形的判定和性质解答即可.【解答】解:∵AB∥CD,∴△ABM∽△DCM,∵AB=CD,△AMB的周长为2∴,∴△CMD的周长为6,故答案为:6【点评】此题考查相似三角形的判定和性质,关键是根据相似三角形的周长之比等于相似比解答.11.(2分)已知点P(﹣4,y1)和Q(﹣1,y2)在反比例函数y=的图象上,则y1与y2的大小关系为y1>y2(填“>”,“<”或“=”)【分析】直接把点P(﹣4,y1)和Q(﹣1,y2)代入反比例函数y=,求出y1,y2的值,并比较大小即可.【解答】解:∵P(﹣4,y1)和Q(﹣1,y2)在反比例函数y=的图象上,∴y1==﹣,y2==﹣2.∵﹣>﹣2,∴y1>y2.故答案为>.【点评】本题考查的是反比例函数图象上点的坐标特征,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.12.(2分)将抛物线y=x2,沿x轴向左平移1个单位后,得到的物线的解析式是y=(x+1)2.【分析】直接利用平移规律“左加右减,上加下减”解题即可.【解答】解:∵将抛物线y=x2,沿x轴向左平移1个单位,∴y=(x+1)2.故得到的抛物线的函数关系式为:y=(x+1)2.故答案为:y=(x+1)2.【点评】主要考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.13.(2分)如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=50°,则∠BAC=25°.【分析】连接OB,根据切线的性质定理以及四边形的内角和定理得到∠AOB=180°﹣∠P=130°,再根据等边对等角以及三角形的内角和定理求得∠BAC的度数.【解答】解:连接OB,∵PA、PB是⊙O的切线,A、B为切点,∴∠PAO=∠PBO=90°,∴∠AOB=360°﹣∠P﹣∠PAO﹣∠PBO=130°,∵OA=OB,∴∠BAC=25°.【点评】此题综合运用了切线的性质定理、四边形的内角和定理、等边对等角以及三角形的内角和定理的应用,主要考查学生的推理和计算能力,注意:圆的切线垂直于过切点的半径.14.(2分)如图,边长为3的正方形OABC的顶点A,C分别在x轴y轴的正半轴上,若反比例数y=的图象与正方形OABC的边有公共点,则k的取值范围是0<k≤9.【分析】由图象可知,当反比例数y=的图象经过B点时,k取最大值,又图象位于第一象限才可能与正方形OABC的边有公共点,进而求出k的取值范围.【解答】解:由题意,可得B(3,3),当反比例数y=的图象经过B点时,k取最大值,此时k=3×3=9,又k>0,所以k的取值范围是0<k≤9.故答案为0<k≤9.【点评】本题考查了反比例函数图象上点的坐标特征,反比例函数的图象与性质,正方形的性质.理解反比例数y=的图象经过B点时,k取最大值是解题的关键.15.(2分)如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果,那么称线段AB被点C黄金分割.黄金分割经常被应用在建筑雪等艺术领域.如图2,在“附中学子故宫行”活动中,同学们沿着紫禁城的中轴线,从内金水桥走到了太和殿,领略了古代建筑的美轮美奂,太和门位于太和殿于内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割,已知太和殿到内金水桥的距离约为100丈,设太和门到太和殿之间的距离为x丈,要求x,则可列方程为x2=100(100﹣x).【分析】根据黄金分割的概念列出比例式,计算即可.【解答】解:设太和门到太和殿的距离为x丈,由题意可得,x2=100(100﹣x),故答案为:x2=100(100﹣x).【点评】本题考查了黄金分割的概念和性质,把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项,叫做把线段AB黄金分割.16.(2分)如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是①③④(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=AD④BE2+CD2=2(AD2+AB2)【分析】只要证明△DAB≌△EAC,利用全等三角形的性质即可一一判断;【解答】解:∵∠DAE=∠BAC=90°,∴∠DAB=∠EAC∵AD=AE,AB=AC,∴△DAB≌△EAC(SAS),∴BD=CE,∠ABD=∠ECA,∵∠DCB﹣∠DCA=∠ACB=45°,显然∠ABD≠∠ACD,故②错误,∵CE﹣BE=BD=BE=DE=AD,故③正确,∵∠ECB+∠EBC=∠ABD+∠ECB+∠ABC=45°+45°=90°,∴∠CEB=90°,即CE⊥BD,故①正确,∴BE2=BC2﹣EC2=2AB2﹣(CD2﹣DE2)=2AB2﹣CD2+2AD2=2(AD2+AB2)﹣CD2.∴BE2+CD2=2(AD2+AB2),故④正确,故答案为①③④【点评】本题考查全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考选择题中的压轴题.三、解答题(本题共6分,第17-22题,每小题5分,第236题,每小题5分,第27-题,每小题5分)17.(5分)计算:tan60°﹣4sin30°cos45°【分析】直接利用二次根式的性质以及特殊角的三角函数值分别化简得出答案.【解答】解:原式=×﹣4××=3﹣2.【点评】此题主要考查了实数运算,正确化简各数是解题关键.18.(5分)如图,在由边长为1个单位的长度的小正方形组成的网格图中,已知点O及△ABC的顶点均为网格线的交点(1)在给定网格中,以O为位似中心,将△ABC放大为原来的三倍,得到请△A'B'C',请画出△A'B'C';(2)B'C'的长度为3单位长度,△A′B′C′的面积为9平方单位.【分析】(1)利用位似图形的性质得出对应点坐标进而得出答案;(2)根据勾股定理和三角形的面积公式即可得到结论.【解答】解:(1)如图所示:△A'B'C'即为所求:(2)如图所示:B'C'的长度==3;∵A′C′=3,∴△A′B′C′的面积为=×3×6=9平方单位,故答案为:3,9.【点评】此题主要考查了位似变换与轴对称变换,得出对应点位置是解题关键.19.(5分)如图,△ABC中,点D在AB上,∠ACD=∠ABC.(1)求证:△ACD∽△ABC;(2)若AD=2,AB=6,求AC的长.【分析】(1)根据两角对应相等的两个三角形相似证明;(2)根据相似三角形的性质列出比例式,计算即可.【解答】(1)证明:∵∠ACD=∠ABC,∠A=∠A,∴ACD∽△ABC;(2)解:∵ACD∽△ABC,∴=,∴AC2=AD•AB=12,解得,AAC=2.【点评】本题考查的是相似三角形的判定和性质,掌握两角对应相等的两个三角形相似是解题的关键.20.(5分)关于x的一元二次方程x2+(2m﹣1)x+m2﹣1=0有两个不相等的实数根(1)求m的取值范围;(2)若m是满足条件的最大整数,求方程的根.【分析】(1)根据判别式的意义得到(2m﹣1)2﹣4(m2﹣1)>0,然后解不等式得到m的范围;(2)取满足条件的最大整数代入方程,再解方程即可.【解答】解:(1)根据题意知,△=(2m﹣1)2﹣4(m2﹣1)>0,解得m<;(2)当m=1时,方程为x2+x=0,解得x1=﹣1,x2=0.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.21.(5分)在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=2,且其顶点在直线y=﹣2x+2上.(1)直接写出抛物线的顶点坐标;(2)求抛物线的解析式.【分析】(1)把x=2代入y=﹣2x+2即可得到结论;(2)把抛物线的顶点坐标为(2,﹣2)代入抛物线的解析式即可得到结论.【解答】解:(1)把x=2代入y=﹣2x+2得,y=﹣2,∴抛物线的顶点坐标为(2,﹣2);(2)∵抛物线的顶点坐标为(2,﹣2);∴抛物线的解析式为:y=(x﹣2)2﹣2,即抛物线的解析式为:y=x2﹣4x+2.【点评】本题考查了待定系数法求二次函数的解析式,二次函数的性质,正确的理解题意是解题的关键.22.(5分)工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.(1)写出该材料温度上升和下降阶段,y与x的函数关系式:①上升阶段:当0≤x≤5时,y=9x+15;②下降阶段:当x>5时,y=.(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?【分析】(1)直接利用待定系数法求出一次函数以及反比例函数的解析式;(2)利用y=30代入结合函数增减性得出答案.【解答】解:(1)①上升阶段:当0≤x<5时,为一次函数,设一次函数表达式为y=kx+b,由于一次函数图象过点(0,15),(5,60),所以,解得:,所以y=9x+15,②下降阶段:当x≥5时,为反比例函数,设函数关系式为:y=,由于图象过点(5,60),所以m=300.则y=;故答案为:9x+15;=(2)当0≤x<5时,y=9x+15=30,得x=,因为y随x的增大而增大,所以x>,当x≥5时,y==30,得x=10,因为y随x的增大而减小,所以x<10,10﹣=,答:可加工min.【点评】此题主要考查了反比例函数的应用,正确得出函数解析式是解题关键.23.(6分)如图,AB是⊙O的直径,过点B做⊙O的切线BC,点D为⊙O上一点,且CD=CB,连结DO 并延长交CB的延长线于点E.(1)求证:CD是⊙O的切线;(2)连接AC,若BE=4,DE=8,求线段AC的长.【分析】(1)证明△COB≌△COD,得到∠ODC=∠OBC=90°,根据切线的判定定理证明;(2)根据切割线定理求出DF,根据勾股定理求出CB,根据勾股定理计算即可.【解答】(1)证明:在△COB和△COD中,,∴△COB≌△COD(SSS),∴∠ODC=∠OBC=90°,∴CD是⊙O的切线;(2)由切割线定理得,BE2=EF•ED,即42=8EF,解得,EF=2,∴FD=DE﹣EF=6,∴AB=DF=6,在Rt△EDC中,DE2+DC2=EC2,即82+BC2=(4+BC)2,解得,BC=6,∴AC==6.【点评】本题考查的是切线的判定定理,切割线定理,全等三角形的判定和性质,掌握切线的判定定理是解题的关键.24.(6分)在平面直角坐标系xOy中,反比例数y=的图象过点A(6,1).(1)求反比例数的表达式;(2)过点A的直线与反比例数y=图象的另一个交点为B,与y轴交点交于点P.①若点P为原点,直接写出点B的坐标;②若PA=2PB,求点P的坐标.【分析】(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出m值,从而得出反比例函数表达式;(2)①根据中心对称的性质即可求得;②作AC⊥y轴于C,BD⊥y轴于D,通过证得△APC∽△BPD,得出==2,求得B的横坐标坐标,代入解析式求得坐标,然后根据待定系数法求得直线AB的解析式,令x=0,即可求得P的坐标.【解答】解:(1)把(6,1)代入反比例函数解析式,得1=,∴m=6;(2)①由于直线过原点,该函数为正比例函数,∵正比例函数和反比例函数图象都是关于原点中心对称的,∴两图象的交点关于原点成中心对称.∴点B、点A关于原点成中心对称.∵A点的坐标为(6,1),∴B点的坐标为(﹣6,﹣1).②作AC⊥y轴于C,BD⊥y轴于D,∵AC∥BD,∴△APC∽△BPD,∴=,∵AP=2PB,∴AC=2BD,∵AC=6,∴BD=3,∴B的横坐标为﹣3,把x=﹣3代入y=得y=﹣2,∴B(﹣3,﹣2),设直线AB的解析式为y=kx+b,把A(6,1),B(﹣3,﹣2)代入得,解得,∴直线AB的解析式为y=x﹣1,令x=0,则y=﹣1,∴P的坐标为(0,﹣1).【点评】本题考查了反比例函数与一次函数的交点及待定系数法求函数解析式,待定系数法求函数解析式是本题的关键.25.(6分)如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D由点A到点B运动的过程中,设AD=xcm,AE=ycm.小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为 2.4或3.3cm.【分析】(1)(2)根据题意测量、作图即可;(3)满足AE=AD条件,实际上可以转化为正比例函数y=【解答】解:(1)根据题意,测量得1.2∴故答案为:1.2(2)根据已知数据,作图得:(3)当AE=AD时,y=,在(2)中图象作图,并测量两个函数图象交点得:AD=2.4或3.3故答案为:2.4或3.3【点评】本题以几何动点问题为背景,考查了函数思想和数形结合思想.在(3)中将线段的数量转化为函数问题,设计到了转化的数学思想.26.(6分)在平面直角坐标系xOy中抛物线y=ax2﹣2ax+3(a≠0)的顶点A在第一象限,它的对称轴与x 轴交于点B,△AOB为等腰直角三角形(1)写出抛物线的对称轴为直线x=1;(2)求出抛物线的解析式;(3)垂直于y轴的直线L与该抛物线交于点P(x1,y1),Q(x2,y2)其中x1<x2,直线L与函数y=(x>0)的图象交于点R(x3,y3),若,求x1+x2+x3的取值范围.【分析】(1)直接根据对称轴公式x=﹣求解可得;(2)将解析式配方成顶点式得其顶点A坐标(1,3﹣a)及对称轴与x轴交点B坐标(1,0),由△AOB 为等腰直角三角形即OB=AB可得1=3﹣a,求得a=2,据此可得答案;(3)先根据抛物线对称性知x1+x2=2且y1=y2>1,由直线L与双曲线交于点R知y3>1,即>1,据此得x3<6;依据知点R一定位于对称轴x=1上或右侧,即x3≥1,从而得出答案.【解答】解:(1)抛物线的对称轴为直线x=﹣=1,故答案为:x=1;(2)∵y=ax2﹣2ax+3=a(x﹣1)2+3﹣a,∴顶点A坐标为(1,3﹣a),。

2019-2020学年北京市海淀区人大附中高三(上)月考物理试卷(12月份)试题数:20.满分:1001.(单选题.3分)用比值法定义物理量是物理学中一种很重要的思想方法.以下属于用比值法定义的物理量是()A.电场强度E= FqB.电场强度E= kQr2C.电容C= ɛS4πkdD.电阻R=ρ lS2.(单选题.3分)下列说法中正确的是()A.磁感应强度B的方向就是小磁针N极所指的方向B.磁感应强度的方向跟产生磁场的电流方向垂直C.磁场中某点磁感应强度的方向.由放在该点的一小段检验电流元所受磁场力方向决定D.在空间某位置放入一小段检验电流元.若这一小段检验电流元不受磁场力作用.则该位置的磁感应强度大小一定为零3.(单选题.3分)如图是“探究影响通电导体在磁场中受力因素”的演示实验示意图局部.三块相同马蹄形磁铁并列放置在水平桌面上.导体棒用图中1、2、3、4柔软细导线悬挂起来.电流可以通过它们之中的任意两根提供.可以认为导体棒所在位置附近为匀强磁场.电流没有在图中画出.关于接通电源时可能出现的实验现象.下列叙述正确的是()A.同时改变电流方向与磁场方向.导体棒摆动方向将会改变B.仅改变电流方向或者仅改变磁场方向.导体棒摆动方向一定改变C.磁铁不变.将电流增强同时改变接线端.导体棒最大摆动角度一定变化D.电流不变.接线端接在1、4之间.去掉中间的磁铁.导体棒最大摆动角度不变4.(单选题.3分)用绝缘柱支撑着贴有小金属箔的导体A和B.使它们彼此接触.起初它们不带电.贴在它们下部的并列平行双金属箔是闭合的.现将带正电荷的物体C移近导体A.发现A和B下部的金属箔都张开一定的角度.如图所示.则()A.导体A和B内部的电场强度不为0B.导体A和B下部的金属箔都感应出负电荷C.如果用一根导线将导体A和B相连.则两金属箔都将闭合D.导体A和B上的感应电荷在A和B内部产生的电场度不为05.(单选题.3分)如图所示.电源电动势为4V.内阻为1Ω.电阻R1=3Ω.R2=R3=4Ω.电流表的内阻不计.闭合S电路达稳定状态后.电容器两极间电压为()A.0B.2.3VC.3VD.3.2V6.(单选题.3分)小芳家正在使用的电器有电灯、洗衣机、电冰箱.小芳从家里的总电能表中测得在时间t内消耗的电能为W.设小芳家的供电电压为U.总电流为I.上述电器的总电阻为R.总功率为P.下列关系式正确的是()A. P=U2RB.W=I2RtC. P=WtD. I=UR7.(单选题.3分)空间某一静电场的电场线与x轴平行.其电场强度E随x变化情况如图所示.图中坐标x1和x2、x2和x3曲线下方的面积相等.设x1、x2、x3三点的电势分别为φ1、φ2、φ3;把一个正电荷从x1移动到x2.电场力做功为W1.从x2移动到x3.电场力做功为W2.下列说法正确的是()A.φ2= φ1+φ32B.φ2<φ1+φ32C.W1>W2D.W1<W28.(单选题.3分)两个相距很近的等量异种点电荷组成的系统称为电偶极子。
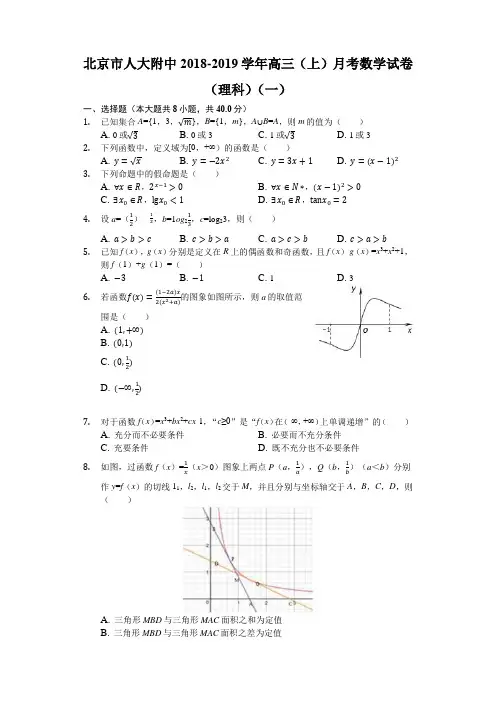
北京市人大附中2018-2019学年高三(上)月考数学试卷(理科)(一)一、选择题(本大题共8小题,共40.0分)1. 已知集合A ={1,3,√m },B ={1,m },A ∪B =A ,则m 的值为( )A. 0或√3B. 0或3C. 1或√3D. 1或3 2. 下列函数中,定义域为[0,+∞)的函数是( )A. y =√xB. y =−2x 2C. y =3x +1D. y =(x −1)2 3. 下列命题中的假命题是( )A. ∀x ∈R ,2x−1>0B. ∀x ∈N ∗,(x −1)2>0C. ∃x 0∈R ,lgx 0<1D. ∃x 0∈R ,tanx 0=2 4. 设a =(12)12,b =1og 213,c =log 23,则( )A. a >b >cB. c >b >aC. a >c >bD. c >a >b5. 已知f (x ),g (x )分别是定义在R 上的偶函数和奇函数,且f (x )-g (x )=x 3+x 2+1,则f (1)+g (1)=( ) A. −3 B. −1 C. 1 D. 3 6. 若函数f(x)=(1−2a)x2(x 2+a)的图象如图所示,则a 的取值范围是( ) A. (1,+∞) B. (0,1)C. (0,12) D. (−∞,12)7. 对于函数f (x )=x 3+bx 2+cx -1,“c ≥0”是“f (x )在(-∞,+∞)上单调递增”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件8. 如图,过函数f (x )=1x (x >0)图象上两点P (a ,1a ),Q (b ,1b )(a <b )分别作y =f (x )的切线11,l 2,l 1,l 2交于M ,并且分别与坐标轴交于A ,B ,C ,D ,则( )A. 三角形MBD 与三角形MAC 面积之和为定值B. 三角形MBD 与三角形MAC 面积之差为定值C. 三角形MBD 的面积一定大于三角形MAC 面积D. 三角形MBD 的面积一定小于三角形MAC 面积二、填空题(本大题共6小题,共30.0分)9. 已知幂函数y =f (x )的图象过(-8,-2),则f (x )=______.10. 当函数f (x )=x 2与函数g (x )=x 2+ax +b 图象关于直线x =1对称时,则a =______,b =______. 11. 若存在x ∈R ,使得不等式12x +1≥a 成立,则实数a 的取值范围是______.12. 为净化水质,向一个游泳池加入某种化学药品,加药后池水中该药品的浓度C (单位:mg /L )随时间t (单位:h )的变化关系为C =20tt 2+4,则经过______h 后池水中药品的浓度达到最大.13. “定义在R 上的函数f (x ),若对任意的x 1,x 2,当x 1≠x 2都有f (x 1)≠f (x 2),则f (x )为单调函数”.能够说明上述命题是错误的一个函数是______. 14. 为了得到函数f (x )=log 2(2x−14)的图象,只需将函数f (x )=log 2x 的图象①先将每一点的横坐标扩大为原来的2倍,再向右移动12个单位即可 ②先右移14个单位,再将每一点的横坐标扩大为原来的2倍即可.③先将每一点横坐标缩为原来的12,再向右移动12个单位,再向下移动2个单位即可 ④先向右移12个单位,再向下移1个单位即可正确的说法有______三、解答题(本大题共3小题,共30.0分)15. 已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=log 2(x +1)(Ⅰ)求函数f (x )的解析式;(Ⅱ)若f (m )<-2,求实数m 的取值范围. 16. 设函数f(x)=(x −1)e x −k2x 2(其中k ∈R ).(1)求函数f (x )的单调区间;(2)当k ≤0时,讨论函数f (x )的零点个数.17.对于任意的n∈N*,记集合E n={1,2,3,…,n},P n={x|x=a∈E n,b∈E n}.若b集合A满足下列条件:①A⊆P n;②∀x1,x2∈A,且x1≠x2,不存在k∈N*,使x1+x2=k2,则称A具有性质Ω.}.∀x1,x2∈P2,且x1≠x2,不存在k∈N*,如当n=2时,E2={1,2},P2={1,222使x1+x2=k2,所以P2具有性质Ω.(Ⅰ)写出集合P3,P5中的元素个数,并判断P3是否具有性质Ω.(Ⅱ)证明:不存在A,B具有性质Ω,且A∩B=∅,使E15=A∪B.(Ⅲ)若存在A,B具有性质Ω,且A∩B=∅,使P n=A∪B,求n的最大值.答案和解析1.【答案】B【解析】解:由题意A∪B=A,即B⊆A,又,B={1,m},∴m=3或m=,解得m=3或m=0及m=1,验证知,m=1不满足集合的互异性,故m=0或m=3即为所求,故选:B.由题设条件中本题可先由条件A∪B=A得出B⊆A,由此判断出参数m可能的取值,再进行验证即可得出答案选出正确选项.本题考查集合中参数取值问题,解题的关键是将条件A∪B=A转化为B⊆A,再由集合的包含关系得出参数所可能的取值.2.【答案】A【解析】解:选项A,y=的定义域为[0,+∞)选项B,y=-2x2定义域为R选项C,y=3x+1定义域为R选项D,y=(x-1)2定义域为R故选:A.选项根据偶次根式下大于等于0可得定义域,选项B、D都是二次函数,定义域为R,选项C是一次函数,定义域为R,可得正确选项.本题主要考查了幂函数、二次函数和一次函数的定义域,属于容易题.3.【答案】B【解析】解:对于A,∀x∈R,2x-1>0,正确,对于B,当x=1时,(x-1)2=0,此时∀x∈N+,(x-1)2>0错误,对于C,当0<x<10时,lgx<1,则∃x0∈R,lgx0<1正确,对于D,tanx的值域为R,∴∃x0∈R,tanx0=2正确,故选:B.根据含有量词的命题的真假判断方法进行判断即可.本题主要考查含有量词的命题的真假判断,比较基础.4.【答案】D【解析】解:∵0<a=()<()0=1,b=1og2<log21=0,c=log23>log22=1,∴c>a>b.故选:D.利用指数函数、对数函数的单调性直接求解.本题考查三个数的大小的比较,考查指数函数、对数函数的单调性等基础知识,考查运算求解能力,是基础题.5.【答案】C【解析】解:由f(x)-g(x)=x3+x2+1,将所有x替换成-x,得f(-x)-g(-x)=-x3+x2+1,根据f(x)=f(-x),g(-x)=-g(x),得f(x)+g(x)=-x3+x2+1,再令x=1,计算得,f(1)+g(1)=1.故选:C.将原代数式中的x替换成-x,再结合着f(x)和g(x)的奇偶性可得f(x)+g(x),再令x=1即可.本题属于容易题,是对函数奇偶性的考查,在高考中,函数奇偶性的考查一般相对比较基础,学生在掌握好基础知识的前提下,做题应该没有什么障碍.本题中也可以将原代数式中的x直接令其等于-1也可以得到计算结果.6.【答案】C【解析】解:∵函数,∴f′(x)=,令f′(x)=0得:x2=a由图可知,函数f(x)有两个极值点,故方程:x2=a有实数解,∴a>0.又从图象中得出,当x>0时,y>0,∴1-2a>0,∴a<故a∈(0,).故选:C.结合函数的图象并利用导函数的性质得a>0,再结合图象在第一象限内的性质得出1-2a>0,即可解答.本题考查了函数的图象、函数的极值与导数的联系,函数值与对应自变量取值范围的关系,解答关键是需要形数结合解题.7.【答案】B【解析】解:函数的导数为f′(x)=3x2+2bx+c,若f(x)在(-∞,+∞)上单调递增,则f′(x)=3x2+2bx+c≥0恒成立,即判别式△=4b2-12c≤0,即c≥b2≥0,即必要性成立,当c≥0时,△=4b2-12c≤0不一定成立,即f′(x)≥0不一定成立,即充分性不成立,则“c≥0”是“f(x)在(-∞,+∞)上单调递增”的必要不充分条件,故选:B.求函数的导数,结合函数单调性与导数之间的关系,以及充分条件和必要条件的定义进行判断即可.本题主要考查充分条件和必要条件的判断,结合函数单调性与导数之间的关系求出c的范围是解:8.【答案】B【解析】解:函数的导数f′(x)=-,则f′(a)=-,f′(b)=-,则11:y-=-(x-a),即y=-x+,①l2:y-=-(x-b)=x+,②由①②得x=,y=,即M(,),分别令x=0,y=0得坐标轴上点的坐标为B(0,),D(0,),C(2b,0),A(2a,0),∵a<b,∴BD=-=,AC=2b-2a,则三角形MBD的面积S△MBD=BDx M=××=,三角形MAC的面积S△MAC=ACy M=×(2b-2a)×=,则S△MBD=S△MAC,即S△MBD-S△MAC=0,即三角形MBD与三角形MAC面积之差为定值,故选:B.求函数的导数,结合导数的几何意义求出切线斜率和方程,求出交点坐标,结合三角形的面积公式进行计算,进行判断即可.本题主要考查三角形面积的计算,结合导数的几何意义求出切线斜率和方程,求出交点坐标,结合三角形的面积公式进行判断是解决本题的关键.9.【答案】x13【解析】解:设幂函数y=f(x)=xα,α∈R,其图象过(-8,-2),∴(-8)α=-2,解得α=,∴f(x)=.故答案为:.利用待定系数法求出幂函数y=f(x)的解析式.本题考查了幂函数的定义与应用问题,是基础题.10.【答案】-4 4【解析】解:根据题意,函数f(x)=x2与函数g(x)=x2+ax+b图象关于直线x=1对称,则g(x)=f(2-x)=(2-x)2=x2-4x+4,则a=-4,b=4;故答案为:-4,4根据题意,分析可得g(x)=f(2-x)=(2-x)2=x2-4x+4,分析可得答案.本题考查函数解析式的求法,关键是掌握函数关于直线对称的性质.11.【答案】a<1【解析】解:存在x∈R,使得不等式≥a成立,即a<,f(x)=,x∈R,f(x)<=1,∴实数a的取值范围是a<1.故答案为:a<1.由题意问题转化为a<,构造函数求出最值即可得出结论.本题考查了不等式恒成立问题,也考查了转化思想,是基础题.12.【答案】2【解析】解:C===5,当且仅当t=2时取等号.因此经过2h后池水中药品的浓度达到最大.故答案为:2.利用基本不等式的性质即可得出.本题考查了基本不等式的性质,属于基础题.13.【答案】f(x)={0,x=0 1x,x≠0【解析】解:根据题意,定义在R上的函数f(x),若对任意的x1,x2,当x1≠x2都有f(x1)≠f(x2),即函数值与自变量是一一对应的关系,且表示单调函数,可以考虑分段函数,则f(x)=,故答案为:f(x)=,(答案不唯一)根据题意,由函数单调性的定义,结合分段函数的性质分析可得答案.本题考查函数的单调性的判定以及性质,注意掌握函数的单调性的定义,属于基础题.14.【答案】①②③④【解析】解:将函数f(x)=log2x的图象对于①,先将每一点的横坐标扩大为原来的2倍,可得y=log2(x)的图象,再向右移动个单位可得y=log2(x-)的图象,故①正确;对于②,先右移个单位,可得y=log2(x-)的图象,再将每一点的横坐标扩大为原来的2倍,可得y=log2(x-)的图象,故②正确;对于③,先将每一点横坐标缩为原来的,可得y=log2(2x)的图象,再向右移动个单位,可得y=log2(2x-1)的图象,再向下移动2个单位,可得y=log2(2x-1)-2=log2的图象,故③正确;对于④,先向右移个单位,可得y=log2(x-)的图象,再向下移1个单位可得y=log 2(x-)-1=log 2(x-)的图象,故④正确. 故答案为:①②③④.运用对数函数的图象变换,主要是伸缩变换和平移变换,即可判断正确结论. 本题考查对数函数的图象变换,考查伸缩变换和平移变换规律,考查转换能力,属于中档题.15.【答案】解:(Ⅰ)∵x >0时,f (x )=log 2(x +1),∴当x <0时,-x >0, ∴f (-x )=log 2(-x +1),∵函数f (x )是定义在R 上的奇函数, ∴f (-x )=-f (x ),∴-f (x )=log 2(-x +1),即f (x )=-log 2(1-x ),又f (0)=0,∴f (x )={log 2(x +1)(x >0)0(x =0)−log 2(1−x)(x <0)…6分(Ⅱ)∵x >0时,f (x )=log 2(x +1)>0,f (0)=0, ∴f (m )<-2⇔到-log 2(1-m )<-2, ∴log 2(1-m )>2, ∴1-m >4, ∴m <-3…12分 【解析】(Ⅰ)根据题意可求得当x <0时的解析式,结合f (0)=0即可得到函数f (x )定义在R 上的解析式;(Ⅱ)由函数f (x )的解析式即可得到log 2(1-m )>2,从而可求得实数m 的取值范围.本题考查对数函数图象与性质的综合应用,考查函数的奇偶性,求得x <0时的解析式是关键,属于中档题.16.【答案】解:(1)函数f (x )的定义域为(-∞,+∞),f '(x )=e x +(x -1)e x -kx =xe x -kx =x (e x -k ),①当k ≤0时,令f '(x )>0,解得x >0,所以f (x )的单调递减区间是(-∞,0),单调递增区间是[0,+∞),②当0<k <1时,令f '(x )>0,解得x <ln k 或x >0,所以f (x )在(-∞,ln k )和(0,+∞)上单调递增,在[ln k ,0]上单调递减, ③当k =1时,f '(x )≥0,f (x )在(-∞,∞)上单调递增,④当k >1时,令f '(x )>0,解得x <0或x >ln k ,所以f (x )在(-∞,0)和(ln k ,+∞)上单调递增,在[0,ln k ]上单调递减;(2)f(0)=-1,①当k<0时,f(1)=−k2>0,又f(x)在[0,+∞)上单调递增,所以函数f(x)在[0,+∞)上只有一个零点,在区间(-∞,0)中,因为f(x)=(x−1)e x−k2x2>x−1−k2x2,取x=2k −1,于是f(2k−1)>(2k−1)−1−k2(2k−1)2=−k2>0,又f(x)在(-∞,0)上单调递减,故f(x)在(-∞,0)上也只有一个零点,所以,函数f(x)在定义域(-∞,+∞)上有两个零点;②当k=0时,f(x)=(x-1)e x在单调递增区间[0,+∞)内,只有f(1)=0.而在区间(-∞,0)内f(x)<0,即f(x)在此区间内无零点.所以,函数f(x)在定义域(-∞,+∞)上只有唯一的零点.【解析】(1)求出函数f(x)的定义域为(-∞,+∞),导函数f'(x),通过①当k≤0时,②当0<k<1时,③当k=1时,④当k>1时,判断导函数的符号,然后判断函数的单调性.(2)f(0)=-1,①当k<0时,判断f(x)在[0,+∞)上单调递增,说明零点个数,f (x)在(-∞,0)上也只有一个零点,推出函数f(x)在定义域(-∞,+∞)上有两个零点;②当k=0时,判断零点个数即可.本题考查函数的单调性的判断与应用,导函数的符号,以及函数的最值,考查转化思想以及分类讨论思想的应用.17.【答案】解:(Ⅰ)∵对于任意的n∈N*,记集合E n={1,2,3,…,n},P n={x|x=√ba∈E n,b∈E n}.∴集合P3,P5中的元素个数分别为9,23,∵集合A满足下列条件:①A⊆P n;②∀x1,x2∈A,且x1≠x2,不存在k∈N*,使x1+x2=k2,则称A具有性质Ω,∴P3不具有性质Ω.…..(6分)证明:(Ⅱ)假设存在A,B具有性质Ω,且A∩B=∅,使E15=A∪B.其中E15={1,2,3,…,15}.因为1∈E15,所以1∈A∪B,不妨设1∈A.因为1+3=22,所以3∉A,3∈B.同理6∈A,10∈B,15∈A.因为1+15=42,这与A具有性质Ω矛盾.所以假设不成立,即不存在A,B具有性质Ω,且A∩B=∅,使E15=A∪B.…..(10分)解:(Ⅲ)因为当n≥15时,E15⊆P n,由(Ⅱ)知,不存在A,B具有性质Ω,且A∩B=∅,使P n=A∪B.若n=14,当b=1时,{x|x=√1a∈E14}=E14,取A1={1,2,4,6,9,11,13},B1={3,5,7,8,10,12,14},则A1,B1具有性质Ω,且A1∩B1=∅,使E14=A1∪B1.当b=4时,集合{x|x=√4a∈E14}中除整数外,其余的数组成集合为{12,32,52,…,132 },令A2={12,52,92,112},B2={32,72,132},则A2,B2具有性质Ω,且A2∩B2=∅,使{12,32,52,…,132}=A2∪B2.当b=9时,集{x|x=9a∈E14}中除整数外,其余的数组成集合{13,23,43,53,73,8 3,103,113,133,143},令A3={13,43,53,103,133},B3={23,73,83,113,143}.则A3,B3具有性质Ω,且A3∩B3=∅,使{13,23,43,53,73,83,103,113,133,143}=A3∪B3.集合C={x|x=√ba∈E14,b∈E14,b≠1,4,9}中的数均为无理数,它与P14中的任何其他数之和都不是整数,因此,令A=A1∪A2∪A3∪C,B=B1∪B2∪B3,则A∩B=∅,且P14=A∪B.综上,所求n的最大值为14.…..(14分)【解析】(Ⅰ)由已知条件能求出集合P3,P5中的元素个数,并判断出P3不具有性质Ω.(Ⅱ)假设存在A,B具有性质Ω,且A∩B=∅,使E15=A∪B.其中E15={1,2,3,…,15},从而1∈A∪B,由此推导出与A具有性质Ω矛盾.从而假设不成立,即不存在A,B具有性质Ω,且A∩B=∅,使E15=A∪B.(Ⅲ)当n≥15时,不存在A,B具有性质Ω,且A∩B=∅,使P n=A∪B.n=14,根据b=1、b=4、b=9分类讨论,能求出n的最大值为14.本题考查集合性质的应用,考查实数值最大值的求法,综合性强,难度大,对数学思维要求高,解题时要认真审题,注意分类讨论思想的合理运用.。


2019年高三12月月考物理含答案一、本题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确,全部选对的得5分,选对但不全的得3分,选错或不答的不得分。
1.物理学在研究实际问题时,常常进行科学抽象,即抓住研究问题的主要特征,不考虑与当前研究问题无关或影响较小的因素,建立理想化模型.以下属于物理学中的理想化模型的是()A. 加速度B. 点电荷C. 质点D.力的合成2.如图所示,两相同轻质硬杆、可绕其两端垂直纸面的水平轴、、转动,在点悬挂一重物M,将两相同木块m紧压在竖直挡板上,此时整个系统保持静止。
表示木块与挡板间摩擦力的大小,表示木块与挡板间正压力的大小。
若挡板间的距离稍许增大后,系统仍静止且、始终等高,则A.变小 B.不变C.变小 D.变大3.质量为m的物体在竖直向上的恒力F作用下减速上升了H,在这个过程中,下列说法中正确的有()A.物体的重力势能增加了mgH B.物体的动能减少了FHC.物体的机械能增加了FH D.物体重力势能的增加小于动能的减少4.2011年8月26日消息,英国曼彻斯特大学的天文学家认为,他们已经在银河系里发现一颗由曾经的庞大恒星转变而成的体积较小的行星,这颗行星完全由钻石构成。
若已知万有引力常量,还需知道哪些信息可以计算该行星的质量()A.该行星表面的重力加速度及绕行星运行的卫星的轨道半径B.该行星的自转周期与星体的半径C.围绕该行星做圆周运动的卫星的公转周期及运行半径D.围绕该行星做圆周运动的卫星的公转周期及公转线速度5.带电粒子射入一个固定的点电荷Q的电场中,沿图中虚线由a点运动到b点,a、b两点到点电荷Q 的距离分别为r a和r b(r a>r b)9若不计重力,则在这一运动过程中()A.电场力对粒子做负功B.粒子在b点的电势能小于在a点的电势能C.粒子在b点的动能大于在a点的动能D.粒子在b点的加速度大于在a点的加速度6. 酒精测试仪用于对机动车驾驶人员是否酒后驾车及其他严禁酒后作业人员的现场检测,它利用的是一种二氧化锡半导体型酒精气体传感器.。

北京市中国人民大学附属中学2019届高三上学期理科月考(二)数学试题(解析版)一、选择题(本大题共8小题)1.函数的值域为A. B.RC. D.【答案】B【解析】【分析】根据函数在定义域上是单调增函数,且满足,判断的值域为R.【详解】解:函数在定义域上是单调增函数,且满足,的值域为R.故选:B.【点睛】本题考查了基本初等函数的单调性与值域应用问题,是基础题.2.若集合,,则是A. B.C. 或D.【答案】C【解析】【分析】化简A,B再根据并集的定义即可求出.【详解】解:由于,即,解得,,由,即,解得或,或,,或,故选:C.【点睛】本题考查集合的并集的运算,解题时要认真审题,熟练掌握并集的概念和运算法则.3.已知是定义在R上的偶函数且以2为周期,则“为上的增函数”是“为上的减函数”的A. 充分而不必要的条件B. 必要而不充分的条件C. 充要条件D. 既不充分也不必要的条件【答案】C【解析】【分析】由题意,可由函数的性质得出在上是减函数,再由函数的周期性即可得出为上的减函数,由此证明充分性,再由为上的减函数结合周期性即可得出为上是减函数,再由函数是偶函数即可得出为上的增函数,由此证明必要性,即可得出正确选项【详解】解:是定义在R上的偶函数,若为上的增函数,则为上是减函数,又是定义在R上的以2为周期的函数,且与相差两个周期,两区间上的单调性一致,所以可以得出为上的减函数,故充分性成立.若为上的减函数,同样由函数周期性可得出为上是减函数,再由函数是偶函数可得出为上的增函数,故必要性成立.综上,“为上的增函数”是“为上的减函数”的充要条件.故选:C.【点睛】本题考查充分性与必要性的判断,解题的关键是理解充分性与必要性证明的方向,即由哪个条件到哪个条件的证明是充分性,那个方向是必要性,初学者易搞不清证明的方向导致表述上出现逻辑错误.4.设函数一定正确的是()A. B.C. D.【答案】D【解析】对于A选项函数的极大值不一定是函数的最大值,所以错;对于B中的是将的图像关于Y轴对称,所以是其极大值点;对于C中的是将的图像关X轴对称,所以才是其极小值点;而对于D中的是将的图像关原点对称,故是其极小值点,故正确.【考点定位】本题主要考查学生对于函数极值与最值关系及函数图像的变换,牢记几种常见变换.属于难度较大的题目.5.设集合,或. 若,则正实数的取值范围是A. B. C. D.【答案】B【解析】作出不等式或表示的区域,可知要想满足,须满足x<0时,,所以6.设,,均为实数,且,,,则()A. B. C. D.【答案】A【解析】【分析】由题意将,,分别看做是两个函数图象交点的横坐标,故画出函数的图象,利用数形结合进行判断即可.【详解】由题意得,,,分别是函数与图象的交点横坐标.在同一坐标系内作出函数的图象,如图所示,由图可得.故选A.【点睛】本题考查函数图象的应用,即结合函数的图象比较大小,解题的关键是根据题意得到,,的几何意义,然后利用数形结合求解,体现了函数图象在解题中的应用.7.若是的最小值,则的取值范围为().A. [-1,2]B. [-1,0]C. [1,2]D.【答案】D【解析】由于当时,在时取得最小值,由题意当时,应该是递减的,则,此时最小值为,因此,解得,选D.8.据统计某超市两种蔬菜连续天价格分别为和,令,若中元素个数大于,则称蔬菜在这天的价格低于蔬菜的价格,记作:,现有三种蔬菜,下列说法正确的是A. 若,,则B. 若,同时不成立,则不成立C. ,可同时不成立D. ,可同时成立【答案】C【解析】特例法:例如蔬菜连续天价格为,蔬菜连续天价格分别为时,,同时不成立,故选C.点睛:本题主要考查了“新定义”问题,属于中档题.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.在该题中,可以采取特例法,直接根据定义得到结果.二、填空题(本大题共6小题)9.定积分______.【答案】【解析】【分析】直接利用牛顿莱布尼兹公式计算定积分即可.【详解】解:由定积分公式可得,故答案为:.【点睛】本题考查定积分的计算,解决本题的关键在于寻找被积函数的原函数,属于基础题.10.若,,,则a,b,c按从大到小的顺序排列依次为______.【答案】【解析】【分析】可看出,从而比较出a,b,c的大小.【详解】解:,,;.故答案为:.【点睛】本题考查指数函数和对数函数的单调性,根据单调性比较数的大小的方法.11.在平面直角坐标系中,若曲线(为常数)过点,且该曲线在点处的切线与直线平行,则.【答案】【解析】曲线过点,则①,又,所以②,由①②解得所以.【考点】导数与切线斜率.【此处有视频,请去附件查看】12.某食品的保鲜时间(单位:时间)与储存温度(单位:℃)满足函数关系,(为自然对数的底数,,为常数).若食品在℃的保险时间设计小时,在℃的保险时间是小时,该食品在℃的保鲜时间是__________小时.【答案】【解析】分析:利用该食品在℃的保险时间设计小时,在℃的保险时间是小时,可得,解得,进而可得结果.详解:∵某食品的保鲜时间(单位:时间)与储存温度(单位:℃)满足函数关系(,是常数).该食品在℃的保险时间设计小时,在℃的保险时间是小时,∴,解得,∴,∴该食品在℃的保鲜时间.故答案为.点睛:本题主要考查指数函数模型解决实际问题,属于中档题.解答本题的关键是利用待定系数法求得,从而使问题得以解决.13.若不等式对于一切恒成立,则实数a的取值范围为______.【答案】【解析】【分析】分离参数a,得,只需求在的最小值【详解】解:,,在的最小值为,实数a的取值范围为.故答案为.【点睛】此题考查求参数范围,一般用分离参数法,进而求函数的值域.14.已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=,n=,现有如下命题:①对于任意不相等的实数x,x2,都有m>0;1②对于任意的a及任意不相等的实数x,x2,都有n>0;1③对于任意的a,存在不相等的实数x,x2,使得m=n;1④对于任意的a,存在不相等的实数x,x2,使得m=-n.1其中真命题有___________________(写出所有真命题的序号).【答案】①④【解析】对于①,因为f '(x)=2x ln2>0恒成立,故①正确对于②,取a=-8,即g'(x)=2x-8,当x1,x2<4时n<0,②错误对于③,令f '(x)=g'(x),即2x ln2=2x+a记h(x)=2x ln2-2x,则h'(x)=2x(ln2)2-2存在x0∈(0,1),使得h(x0)=0,可知函数h(x)先减后增,有最小值.因此,对任意的a,m=n不一定成立.③错误对于④,由f '(x)=-g'(x),即2x ln2=-2x-a令h(x)=2x ln2+2x,则h'(x)=2x(ln2)2+2>0恒成立,即h(x)是单调递增函数,当x→+∞时,h(x)→+∞当x→-∞时,h(x)→-∞因此对任意的a,存在y=a与函数h(x)有交点.④正确考点:本题主要考查函数的性质、函数的单调性、导数的运算等基础知识,考查函数与方程的思想和数形结合的思想,考查分析问题和解决能提的能力.【此处有视频,请去附件查看】三、解答题(本大题共2小题,共30.0分)15.已知函数.当时,求曲线在处的切线方程;讨论函数的单调性;当时,求函数在区间的最小值.【答案】(1);(2)详见解析;(3)详见解析.【解析】【分析】当时,,求其导函数,得到,又,可得曲线在处的切线方程为;求出原函数的导函数,分,,三类求函数的单调区间;由知,当时,的减区间为,增区间为,然后分,,三类求函数的最小值.【详解】解:当时,,.,又,曲线在处的切线方程为;.当时,,在上为增函数;当时,在上有,当上,有,的减区间为,增区间为;当时,在上有,当上,有,的减区间为,增区间为;由知,当时,的减区间为,增区间为,若,即时,在单调递增,;若,即,在上单调递减,在上单调递增,;若,即时,在单调递减,.综上,.【点睛】本题考查利用导数求过曲线上某点处的切线方程,考查利用导数研究函数的单调性及最值,体现了分类讨论的数学思想方法,是中档题.16.若函数在定义域内存在实数x,满足,则称为“局部奇函数”.已知函数,试判断是否为“局部奇函数”?并说明理由;设是定义在上的“局部奇函数”,求实数m的取值范围;若为定义域R上的“局部奇函数”,求实数m的取值范围.【答案】(1)是“局部奇函数”;(2);(3).【解析】【分析】运用两角和与差的正弦公式,化简,再由由局部奇函数的定义,即可判断;根据局部奇函数的定义,可得方程在上有解,运用换元法,令,则,求出右边的值域即可;根据“局部奇函数”的定义可知,有解即可设,则,即有方程等价为在时有解,设,由对称轴和区间的关系,列出不等式,解出即可.【详解】解:由于,,则,由于,则,当时,成立,由局部奇函数的定义,可知该函数为“局部奇函数”;根据局部奇函数的定义,时,可化为,因为的定义域为,所以方程在上有解,令,则,设,则,当时,,故在上为减函数,当时,,故在上为增函数,所以时,所以,即.根据“局部奇函数”的定义可知,函数有解即可,即,,即有解即可.设,则,方程等价为在时有解,设,对称轴,若,则,即,,此时,若,要使在时有解,则,即,解得,综上得,【点睛】本题考查新定义的理解和运用,考查方程有解的条件及二次函数的图象和性质的运用,以及指数函数的图象和性质的运用,考查运算能力,属于中档题和易错题.。
北京人大附中2019届九年级上学期12月月考数学试卷一、选择题(本题共16分,每小题2分)第1-8题有四个选项,符合题意的选项只有一个1.(2分)在Rt△ABC中,∠C=90°,BC=4,AB=5,则sin A的值为()A.B.C.D.2.(2分)二次函数y=(x﹣5)2+7的最小值是()A.﹣7B.7C.﹣5D.53.(2分)如图,DE∥BC,AD:DB=2:3,EC=6,则AE的长是()A.3B.4C.6D.104.(2分)如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°5.(2分)如图,点A在双曲线y=上,B在y轴上,且AO=AB,若△ABO的面积为6,则k的值为()A.6B.﹣6C.12D.﹣126.(2分)北京教育资源丰富,高校林立,下面四个高校校徵主题图案中,既不是中心对称图形,也不是轴对称图形的是()A.北京林业大学B.北京体育大学C.北京大学D.中国人民大学7.(2分)如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为12米,若小明的眼晴与地面的距离为1.5米,则旗杆的高度为()A.9B.12C.14D.188.(2分)根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.下列叙述正确的是()A.运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同B.运动员高强度运动后,最高血乳酸浓度大约为250mg/LC.采用慢跑活动方式放松时,运动员必须慢跑70min后才能基本消除疲芳D.运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用跑活动方式来放松二、填空题(本题共16分,每小题2分)9.(2分)sin A=,则锐角A=度.10.(2分)如图,AB∥CD,AB=CD,线段AD与BC交于点M,△AMB的周长为2,则△CMD的周长为.11.(2分)已知点P(﹣4,y1)和Q(﹣1,y2)在反比例函数y=的图象上,则y1与y2的大小关系为y1y2(填“>”,“<”或“=”)12.(2分)将抛物线y=x2,沿x轴向左平移1个单位后,得到的物线的解析式是.13.(2分)如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=50°,则∠BAC=.14.(2分)如图,边长为3的正方形OABC的顶点A,C分别在x轴y轴的正半轴上,若反比例数y=的图象与正方形OABC的边有公共点,则k的取值范围是.15.(2分)如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果,那么称线段AB被点C黄金分割.黄金分割经常被应用在建筑雪等艺术领域.如图2,在“附中学子故宫行”活动中,同学们沿着紫禁城的中轴线,从内金水桥走到了太和殿,领略了古代建筑的美轮美奂,太和门位于太和殿于内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割,已知太和殿到内金水桥的距离约为100丈,设太和门到太和殿之间的距离为x丈,要求x,则可列方程为.16.(2分)如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=AD④BE2+CD2=2(AD2+AB2)三、解答题(本题共6分,第17-22题,每小题5分,第236题,每小题5分,第27-题,每小题5分)17.(5分)计算:tan60°﹣4sin30°cos45°18.(5分)如图,在由边长为1个单位的长度的小正方形组成的网格图中,已知点O及△ABC的顶点均为网格线的交点(1)在给定网格中,以O为位似中心,将△ABC放大为原来的三倍,得到请△A'B'C',请画出△A'B'C';(2)B'C'的长度为单位长度,△A′B′C′的面积为平方单位.19.(5分)如图,△ABC中,点D在AB上,∠ACD=∠ABC.(1)求证:△ACD∽△ABC;(2)若AD=2,AB=6,求AC的长.20.(5分)关于x的一元二次方程x2+(2m﹣1)x+m2﹣1=0有两个不相等的实数根(1)求m的取值范围;(2)若m是满足条件的最大整数,求方程的根.21.(5分)在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=2,且其顶点在直线y=﹣2x+2上.(1)直接写出抛物线的顶点坐标;(2)求抛物线的解析式.22.(5分)工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.(1)写出该材料温度上升和下降阶段,y与x的函数关系式:①上升阶段:当0≤x≤5时,y=;②下降阶段:当x>5时,y.(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?23.(6分)如图,AB是⊙O的直径,过点B做⊙O的切线BC,点D为⊙O上一点,且CD=CB,连结DO并延长交CB的延长线于点E.(1)求证:CD是⊙O的切线;(2)连接AC,若BE=4,DE=8,求线段AC的长.24.(6分)在平面直角坐标系xOy中,反比例数y=的图象过点A(6,1).(1)求反比例数的表达式;(2)过点A的直线与反比例数y=图象的另一个交点为B,与y轴交点交于点P.①若点P为原点,直接写出点B的坐标;②若PA=2PB,求点P的坐标.25.(6分)如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D 由点A到点B运动的过程中,设AD=xcm,AE=ycm.小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为cm.26.(6分)在平面直角坐标系xOy中抛物线y=ax2﹣2ax+3(a≠0)的顶点A在第一象限,它的对称轴与x轴交于点B,△AOB为等腰直角三角形(1)写出抛物线的对称轴为直线;(2)求出抛物线的解析式;(3)垂直于y轴的直线L与该抛物线交于点P(x1,y1),Q(x2,y2)其中x1<x2,直线L与函数y=(x>0)的图象交于点R(x3,y3),若,求x1+x2+x3的取值范围.27.(7分)如图,∠MON=α(0<α<90°),A为OM上一点(不与O重合),点A关于直线ON的对称点为B,AB与ON交于点C,P为直线ON上一点(不与O,C重合)将射线PB绕点P顺时针旋转β角,其中2α+β=180°,所得到的射线与直线OM交于点Q这个问题中,点的位置和角的大小都不确定,在这里我们仅研究两种特殊情况,一般的情况留给同学们深入探索(1)如图1,当α=45°时,此时β=90°,若点P在线段OC的延长线上①依题意补全图形;②求∠PQA﹣∠PBA的值;(2)如图2,当α=60°,点P在线段CO的延长线上时,用等式表示线段OC,OP,AQ之间的数量关系,并证明.28.(7分)对于平面直角坐标系xOy中的⊙C和点P,给出如下定义若在⊙C上存在一点Q,使得△PCQ是以CQ为底边的等腰三角形且底角∠PCQ≤60°,则称点P为⊙C的“邻零点”,(1)当⊙O的半径为2时,①在点P1(﹣2,0),P2(1,﹣1),P3(0,3)中,⊙O的“邻零点”是;②点P在直线y=﹣x上,若P为⊙O的“邻零点”,求点P的横坐标x P的取值范围.(2)⊙C的圆心在x轴上,半径为4,直线y=2x+2与x轴,y轴分别交于点A,B,若线段AB上的点都是⊙C的“邻零点”,直接写出圆心C的横坐标t的取值范围.。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面上满足条件的复数z所对应的点的轨迹是( )A. 椭圆B. 直线C. 线段D. 圆【答案】C【解析】设(),由,得,所以,即点到两点和的距离和为,所以复数在复平面上对应点的轨迹为线段,故选C.2.若集合( )A. B. C. D.【答案】C【解析】应选C分析:由集合A和B的取值范围,找出它们的公共部分,就得到集合A∩B.解答:解:∵A={x|-1≤x≤1},B=∴A∩B═{x|-1≤x≤1}∩="{x|0≤x≤1" }.故答案为:C点评:本题考查交集的运算,解题时要认真审题,注意公式的合理运用.3.某同学用收集到的6组数据对(其中)制作成如图所示的散点图(点旁的数据为该点坐标),并由最小二乘法计算得到回归直线l的方程为,相关系数为r.现给出以下3个结论:( )①r>0;②直线l恰好过点D.③>1;其中正确结论是A. ①②B. ①③C. ②③D. ①②③【答案】A【解析】由图可知这些点分布在一条斜率大于零的直线附近,所以为正相关,即相关系数因为所以回归直线的方程必过点,即直线恰好过点;因为直线斜率接近于AD斜率,而,所以③错误,综上正确结论是①②,选A.4.数列的前n项之和为( )A. B. C. D.【答案】C【解析】【分析】通过题干条件得到数列是由一个等差和一个等比数列构成的,故按照各自的求和公式进行分组求和即可.【详解】数列的通项为:,求和可以分为一个等差数列,首项为2,公差为1,和一个等比数列,首项为,公比为,将两个数列分别求和,=化简得到.故答案为:C.【点睛】这个题目考查了等差数列和等比数列的求和公式的应用,也考查了分组求和的方法,较基础. 数列求和常用法有:错位相减,裂项求和,分组求和等。
5.曲线在点(0,1)处的切线方程是( )A. B. C. D.【答案】A【解析】【分析】求出函数的导数,求出切线方程的斜率,即可得到切线方程.【详解】曲线,解得y′=e x+xe x,所以在点(0,1)处切线的斜率为1.曲线在点(0,1)处的切线方程是:y﹣1=x.即x﹣y+1=0.故选:A.【点睛】本题考查曲线的切线方程的求法,考查计算能力6.在△中,为的中点,点满足,则A. B.C. D.【答案】A【解析】【分析】利用向量共线的性质得,,再利用向量的三角形法则、即可得出结果. 【详解】为的中点,点满足,,故选A.【点睛】本题考查了向量三角形法则、向量共线性质,属于基础题.向量的运算有两种方法,一是几何运算往往结合平面几何知识和三角函数知识解答,运算法则是:(1)平行四边形法则(平行四边形的对角线分别是两向量的和与差);(2)三角形法则(两箭头间向量是差,箭头与箭尾间向量是和);二是坐标运算:建立坐标系转化为解析几何问题解答(求最值与范围问题,往往利用坐标运算比较简单).7.将半径为,圆心角为的扇形围成一个圆锥,则该圆锥的内切球的体积为A. B.C. D.【答案】A【解析】【分析】先求圆锥的底面半径以及高,再根据相似得内切球的半径,最后根据球的体积公式求结果. 【详解】设圆锥的底面半径为r,高为h,则,设内切球的半径为R,则选A.【点睛】本题考查圆锥展开图相关知识,考查基本求解能力.8.曲线与曲线的()A. 长轴长相等B. 短轴长相等C. 离心率相等D. 焦距相等【答案】C【解析】曲线可得:,曲线可得:由此可得只有其离心率时相等的9.设,其中,则函数内的零点个数是( )A. 0B. 1C. 2D. 与n有关【答案】B【解析】【分析】先利用导数判断在上单调递增,再利用零点存在定理可得结果.【详解】由,知在上单调递增,,,根据零点存在定理可得在零点的个数只有个,故选B.【点睛】判断函数零点个数的常用方法:(1) 直接法:令则方程实根的个数就是函数零点的个;(2) 零点存在性定理法:判断函数在区间上是连续不断的曲线,且再结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数;(3) 数形结合法:转化为两个函数的图象的交点个数问题.10.右图是一个算法流程图,若输入的值是,输出的值是,则的取值范围是( )A. B.C. D.【答案】D【解析】执行程序框图,输入,第一次循环;第二次循环;第三次循环;第四次循环;第五次循环,此时结束输出,所以的取值范围是,故选D.11.直线与椭圆交于A、B两点,以线段AB为直径的圆恰好经过椭圆的右焦点,则椭圆C的离心率为( )A. B.C. D.【答案】D【解析】依题意,以为直径的圆过椭圆的右焦点,也过左焦点,以这两个焦点和两点得到一矩形,直线的倾斜角为,所以矩形的宽为,长为.根据椭圆的定义有,故.点睛:本题主要考查直线与圆锥曲线的位置关系,考查椭圆的几何性质和圆的几何性质,还考查了椭圆的对称性.解题的关键是判断两个焦点与两点所组成的四边形为矩形,再结合直线的倾斜角,和椭圆的定义,可求得关于的一个方程,将方程化为离心率即可求得离心率.12.在空间直角坐标系中,O为原点,平面内有一平面图形由曲线轴围成,将该图形按空间向量进行平移,平移过程中平面图形所划过的空间构成一个三维空间几何体,该几何体的体积为( )A. B. C. D.【答案】A【解析】【分析】根据题意得到所划过的空间构成的是以半径为2的半圆为上下底面,高为2的斜圆柱,再由祖暅定理得到结果.【详解】平面图形是以O为圆心,2为半径的半圆,将该圆按照空间向量进行平移,所划过的空间构成的是以半径为2的半圆为上下底面,高为2的斜圆柱,由祖暅原理,斜圆柱体积计算方法和直圆柱的计算方法相同,故答案为:A.【点睛】这个题目考查了立体图形的体积的计算,以及学生的空间想像能力,也涉及祖暅原理的应用,题目中等难度.第Ⅱ卷(90分)二、填空题:本大题共4小题,每小题5分,共20分.13.若满足约束条件目标函数的最小值为2,则a= ________.【答案】【解析】【分析】结合前两个不等式可知,作出可行域的大致形状,化目标函数为斜截式直线方程,数形结合可知当过区域内的点A时,直线在轴上的截距最小,联立方程组求出点坐标和的值.【详解】作出约束条件的可行域,如图所示,结合前两个不等式可知;目标函数,转化成直线,当截距取最小值目标函数对应最小值.由图可知,当直线过点A时取得最小截距.联立方程组,解得故答案为1.【点睛】本题主要考查线性规划的含参问题,数形结合是解决问题的关键.目标函数型线性规划问题解题步骤(含参问题求参数也适用):(1)确定可行区域(2)将转化为,求z的值,可看做求直线,在y轴上截距的最值。
北京人大附中2019 届九年级上月考数学试卷(12 月)含答案解析一、选择题(本题共32 分,每小题 4 分)1.反比例函数y=的图象不一定经过点( )A .(﹣ 3, 1) B.(﹣ 3,﹣ 1)C.( 1,3)D.(,2)2.下列图形中,不是轴对称图形的是( )A .B.C.D.3.随机抛掷一枚质地均匀的硬币两枚,两次都是正面朝上的概率是( )A .B.C.D.4.如图,⊙ O 的直径 AB=8 ,弦 DE 经过 OB 的中点 C 且 DE ⊥ OB,则弦 DE 的长为 ( )A . 3B. 2C. 4D. 65.如图,正△ ABC 的边长为3,以 A 为圆心, AB 为半径作弧,则图中阴影部分的面积是( )A .B.C.﹣D. 36.如图,四边形ABCD 中, AB=AC=AD ,∠ CBD=23 °,则∠ CAD 为 ( )A . 47°B . 46°C. 45°D. 44°7.如图, AB 为⊙ O 的一条固定直径,自左半圆上一点C,作弦 CD⊥AB ,∠ OCD 的平分线交⊙ O 于点 E,当点 C 在左半圆(不包括 A ,B 两点)上移动时,关于点 E 的说法:①到 CD 的距离始终不变;② 位置始终不变;③ 始终平分;④位置随点 C 的移动而移动,正确的是 ( )A .①②B.②③C.②D.④8.如图,正△ ABC 的边长为 3,点 N 在 AC 从点 A 出发,沿 A →B→C 的方向运动,到达点边上且 AN : NC=1 : 2,三角形边上的动点M C 时停止.设点 M 运动的路程为 x,y=MN 2,则 y 关于 x 的函数图象大致为( )A .B.C.D.二、填空题(本题共16 分,每小题 4 分)9.如图, DE ∥BC , AD : DB=2 : 3, EC=6,则 AE 的长是 __________.10.在 Rt△ABC 中,∠ C=90 °,AC=5 , AB=13 , tanA 的是 __________ .11.如,用一个交叉卡(OA=OB , OC=OD )量零件的内孔直径AB ,若 OC:OA=1 : 2,且量的CD=12mm ,零件的内孔直径AB 是 __________mm .12.如,△ ABC 中, AB=AC=1 ,∠ ABC=72 °, BB 1平分∠ ABC 交 AC 于 B1, B1做 B1B 2∥BC 交 AB 于 B2,作 B2B 3平分∠ AB 2B 1交 AC 于 B3, B3作 B 3B4∥ BC 交 AB 于B4,⋯段 B1B 2的度 __________ ,段 B 2n﹣1B2n的度 __________ .三、解答(本共30 分,每小 5 分)13.用配方法解方程:.14.算: 3sin30°2cos 45°+2tan60°cos30°.15.如,△ ABC 与△ADE 都是等腰直角三角形,且∠ BAC= ∠ DAE=90 °,找出一条与段 CE 相等的段(以中已知点的端点),画出条段并出明.16.已知 m 是方程 x 2﹣ x ﹣3=0 的根,求代数式( 1+) ?( m ﹣ 3)的值.17.如图,半径为 5 的⊙ O 中, AB 是直径,弦 BC=8 ,OD ⊥ AB 交 BC 于 D ,求 CD 的长及△ OCD 的面积.18.列方程或方程组解应用题:150 元,双人间每天每间 140 元,为了某酒店有三人间、双人间的客房,三人间每天每间吸引游客,实行团体入住五折优惠措施,一个50 人的旅游团优惠期间到该酒店入住,住了 一些三人间和双人间客房,若每间客房正好住满且一天共花去住宿费1510 元,则该旅行团 住了三人间和双人间客房各多少间?四、解答题(本题共20 分,每小题 5 分)19.如图,直线 y=﹣ 2x+1 分别交 x 轴, y 轴于点 A , B ,交反比例函数 y= 的图象于点 C , CB : BA=2 : 1.(1)求反比例函数 y= 的解析式;(2)若点 P 在 y 轴上且以点 B , C ,P 为顶点的三角形与 △ AOB 相似,直接写出点 P 的坐标.20.如图,已知,在△ ABC 中,∠ ABC=90 °, BC 为⊙ O 的直径, AC 与⊙ O 交于点 D,点E 为 AB 的中点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.(1)求证: ED 是⊙ O 的切线;(2)如果 CF=1, CP=2, sinA=,求⊙ O的直径BC.21 .据报道,历经一年半的调查研究, PM 2.5 源解析已经通过专家论证.各种调查显示,机动车成为 PM 2.5 的最大来源,一辆车一天行驶 20 千米,那么这辆车每天至少就要向大气里排放 0035 千克污染物.以下是相关的统计图、表:年全年空气质量等级天数统计表空气质量等级优良轻度污中度污重度污严重污染染染染天数(天)41 135 84 47 45 13(1)请根据所给信息补全扇形统计图;(2)请你根据“年全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到 0.01)(3)小明是社区环保志愿者,他和同学们调查了本社区的100 辆机动车,了解到其中每天出行超过 20 千米的有 40 辆.已知年机动车保有量已突破 520 万辆,请你通过计算,估计年一天中出行超过 20 千米的机动车至少要向大气里排放多少千克污染物?22.如图 1,给定锐角三角形ABC ,小明希望画正方形 DEFG ,使 D, E 位于边 BC 上,F, G 分别位于边 AC , AB 上,他发现直接画图比较困难,于是他先画了一个正方形HIJK ,是的 H, I ,位于射线 BC 上, K 位于射线 BA 上,而不需要求 J 必须位于 AC上.这是他发现可以将正方形HIJK 通过放大或缩小得到满足要求的正方形DEFG .阅读以上材料,回答小明接下来研究的以下问题:(1)如图 2,给定锐角三角形ABC ,画出所有长宽比为 2: 1 的长方形 DEFG ,使 D , E 位于边 BC 上, F, G 分别位于边AC , AB 上.(2)已知三角形 ABC 的面积为 36, BC=12 ,在第( 1)问的条件下,求长方形 DEFG 的面积.五、解答题(本题共22 分,第 23 题 7 分,第 24 题 7 分,第 25 题 8 分)23.已知关于 x 的二次函数 y 1=x 2﹣( m+3) x+m+2 , y 2=﹣ x 2+bx+c .(1)求证:方程 x 2﹣( m+3 ) x+m+2=0 必有实根;(2)若 m 为整数, y 1 的图象与 x 轴有一个交点的横坐标 a 满足 5< a < 7,求 m 的值;(3)在第( 2)问的条件下,小明利用函数图象解关于x 的不等式 y 1 <y 2,正确解得该不等式的解 集为 3< x <4,求 y 2 的解析式.24.过正方形 ABCD 的顶点 A 任作一条直线 l ( l 不过点 B ,C , D ) ,过点 B ,C ,D 作 l的垂线段 BF ,CG ,DH .( 1)如图 1,若直线 l 过线段( 2)如图 2,若直线 l 与线段BC 的中点 E ,则 BF : CG : DH=__________ .BC 相交于点 E ,则 BF , CG , DH 满足等量关系式 __________,请证明你的猜想;(3)如果直线 l 与线段 CB 的延长线相交,直接写出BF , CG , DH 满足的等量关系式__________,在直线 l 旋转一周的过程中( l 不过点 B , C , D ),直接写出 y=的取值范围 __________.25.定义:在平面直角坐标系 xOy 中,给定两点 M ( x M , y M ), N ( x N , y N ),对于给定的实数 a , b ,作 a|x M ﹣x N |+b|y M ﹣ y N |为 M , N 的权重为 a , b 的直角距离,记为 d xy ( M ,N ),例如: d 2, 3(( 1, 0),( 4, 7)) =2|1﹣4|+3|0﹣ 7|=27. 特别地,权重为 1、1 的直角距离,又称为等权重距离,则记为 d ( M ,N ),例如: d(( 1, 0),( 4, 7)) =|1﹣4|+|0﹣ 7|=10. 根据以上定义,回答以下问题:(1) d (( 0, 0),(﹣ 3,﹣ 2)) =__________, d 3, 2(( 0, 0),(﹣ 1, 2)) =__________ .(2) P 为直线 y=2x+4 上一动点,求 OP 的等权重距离的最小值及此时 P 点的坐标; (3) P 为直线 y=2x+4 上一动点, Q 为以 O 为圆心的单位圆上的动点,则 d ( P , Q )的最 小值是 __________ ,d 3,2( P , Q )的最小值是 __________.-学年人大附中九年级(上)月考数学试卷(12 月份)一、选择题(本题共32 分,每小题 4 分)1.反比例函数 y= 的图象不一定经过点( )A .(﹣ 3, 1) B.(﹣ 3,﹣ 1)C.( 1,3)D.(, 2)【考点】反比例函数图象上点的坐标特征.【分析】根据反比例函数图象上点的坐标特点即可得出结论.【解答】解: A 、∵(﹣ 3)×1=﹣3≠3,∴函数图象不过此点,故本选项正确;B、∵(﹣ 3)×(﹣ 1) =3,∴函数图象过此点,故本选项错误;C、∵3×1=3 ,∴函数图象过此点,故本选项错误;D、∵×2=3,∴函数图象不过此点,故本选项错误.故选 A .【点评】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.2.下列图形中,不是轴对称图形的是( )A .B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解.【解答】解: A 、不是轴对称图形,故本选项正确;B、是轴对称图形,故本选项错误;C、是轴对称图形,故本选项错误;D、是轴对称图形,故本选项错误.故选 A .【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.3.随机抛掷一枚质地均匀的硬币两枚,两次都是正面朝上的概率是( )A .B.C.D.【考点】列表法与树状图法.【分析】列举出所有情况,看正面都朝上的情况数占总情况数的多少即可.【解答】解:共 4 种情况,正面都朝上的情况数有 1 种,所以概率是.故选 B .【点评】本题考查了概率的求法;用到的知识点为:概率=所求情况数与总情况数之比.得到所求的情况数是解决本题的关键.4.如图,⊙ O 的直径 AB=8 ,弦 DE 经过 OB 的中点 C 且 DE ⊥ OB,则弦 DE 的长为 ( )A . 3B. 2C. 4D. 6【考点】垂径定理;勾股定理.【分析】连接 OD ,先求出OD 及 OC 的长,再由勾股定理求出DE 的长即可.【解答】解:连接 OD,∵⊙ O 的直径 AB=8 ,弦 DE 经过 OB 的中点 C 且 DE ⊥ OB,∴O D=4 , OC=2, DE=2CD .∵CD===2,∴DE=2CD=4.故选: C.【点评】本题考查的是垂径定理和勾股定理的应用,掌握垂直于弦的直径平分弦并且平分弦所对的弧是解题的关键.5.如图,正△ ABC 的边长为3,以 A 为圆心, AB 为半径作弧,则图中阴影部分的面积是( )A .B.C.﹣D. 3【考点】扇形面积的计算.【分析】根据等边三角形的面积公式求出正△ ABC 的面积,根据扇形的面积公式S= 求出扇形的面积,求差得到答案.【解答】解:∵正△ABC 的边长为3,∴正△ ABC 的面积为×3×= ,扇形 ABC 的面积为= ,则图中阴影部分的面积是﹣.故选: C.【点评】本题考查的是等边三角形的性质和扇形的面积计算,掌握扇形的面积公式S=是解题的关键.6.如图,四边形ABCD 中, AB=AC=AD,∠ CBD=23°,则∠CAD为()A. 47°B . 46°C. 45°D. 44°【考点】圆周角定理.【分析】先根据四边形 ABCD 中, AB=AC=AD 可知, B、 C、 D 三点在以 A 为圆心, AD 为半径的圆上,再由圆周角定理即可得出结论.【解答】解:∵四边形 ABCD 中, AB=AC=AD ,∴B 、 C、 D 三点在以 A 为圆心, AD 为半径的圆上.∵∠ CBD=23 °,∴∠ CAD=2 ∠CBD=46 °.故选 B .【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.7.如图, AB 为⊙ O 的一条固定直径,自左半圆上一点C,作弦 CD⊥AB ,∠ OCD 的平分线交⊙ O 于点 E,当点 C 在左半圆(不包括 A ,B 两点)上移动时,关于点 E 的说法:①到 CD 的距离始终不变;② 位置始终不变;③ 始终平分;④位置随点 C 的移动而移动,正确的是 ( )A .①②B.②③C.②D.④【考点】圆周角定理;垂径定理.【分析】连接 OE,由 CE 平分∠ OCD ,得到∠ 1=∠ 2,而∠ 1=∠ E,所以有 OE∥ CD,则OE⊥AB ,即可得到 OE 平分半圆 AEB .【解答】解:连 OE,如图,∵CE 平分∠ OCD ,∴∠ 1=∠ 2,而OC=OE ,有∠ 1=∠ E,∴∠ 2=∠ E,∴OE∥ CD ,∵点 O 到 CD 的距离在变,∴点 E 到 CD 的距离发生变;故①错误;又∵弦 CD ⊥AB ,∴OE⊥ AB ,∴OE 平分半圆AEB ,即点 E 是半圆的中点,∴点 E 位置始终不变;故② 正确.故选 C.【点评】本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了垂径定理的推论.8.如图,正△ ABC 的边长为 3,点 N 在 AC 边上且 AN : NC=1 : 2,三角形边上的动点M 从点 A 出发,沿 A →B→C 的方向运动,到达点 C 时停止.设点M 运动的路程为x,y=MN 2,则 y 关于 x 的函数图象大致为 ( )A .B.C.D.【考点】动点问题的函数图象.【分析】注意分析y 随 x 的变化而变化的趋势,而不一定要通过求解析式来解决.【解答】解:∵等边三角形ABC 的边长为3, N 为 AC 的三等分点,∴AN=1 .∴当点 M 位于点 A 处时, x=0, y=1 .①当动点 M 从 A 点出发到 AM=0.5 的过程中, y 随 x 的增大而减小,故排除 D ;②当动点 M 到达 C 点时, x=6 , y=4,即此时 y 的值与点M 在点 A 处时的值不相等.故排除A 、C.故选: B.【点评】本题考查了动点问题的函数图象,解决本题应首先看清横轴和纵轴表示的量,然后根据动点的行程判断 y 的变化情况.二、填空题(本题共16 分,每小题 4 分)9.如图, DE ∥BC , AD : DB=2 : 3, EC=6,则 AE 的长是 4.【考点】平行线分线段成比例.【专题】计算题.【分析】根据平行线分线段成比例定理得到=,即=,然后利用比例性质求AE .【解答】解:∵ DE ∥ BC ,∴=,即=∴A E=4 .故答案为 4.【点评】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.10.在 Rt△ABC 中,∠ C=90 °,AC=5 , AB=13 ,则 tanA 的值是.【考点】锐角三角函数的定义.【分析】根据勾股定理,可得BC 的长,根据正切函数的定义,可得答案.【解答】解:在 Rt△ABC 中,∠ C=90°,AC=5 , AB=13 ,由勾股定理,得BC===12 ,tanA==,故答案为:.【点评】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.11.如图,用一个交叉卡钳(OA=OB , OC=OD )测量零件的内孔直径AB ,若 OC:OA=1 : 2,且量的CD=12mm ,则零件的内孔直径AB 是 24mm.【考点】相似三角形的用.【】算.【分析】由于 OC: OA=OD : OB=1 :2,加上∠ COD= ∠ AOB ,可判断△COD ∽△ AOB ,然后利用相似比开始算出AB .【解答】解:∵ OC:OA=OD : OB=1 : 2,而∠ COD= ∠ AOB ,∴△ COD ∽△ AOB ,∴= = ,∴A B=2CD=2 ×12mm=24mm .故答案 24.【点】本考了相似三角形的用:利用点和盲区的知构建相似三角形,用相似三角形的比相等的性求物体的高度或度.12.如,△ ABC 中, AB=AC=1 ,∠ ABC=72 °, BB 1平分∠ ABC 交 AC 于 B1, B1做 B1B 2∥BC 交 AB 于 B2,作 B2B 3平分∠ AB 2B 1交 AC 于 B3, B3作 B 3B4∥ BC 交 AB 于B4,⋯段 B1B 2的度,段B2n﹣1B2n的度()n﹣2.【考点】相似三角形的判定与性.【分析】因 B1作 B 1B2∥BC 交 AB 于 B2,于是得到△ AB 2B1∽△ ABC ,得到成比例,因AB=AC=m ,∠ ABC=72 °, BB 1平分∠ ABC 交 AC 于 B1,所以△ BCB 1和△B 2B1B 是等腰三角形,根据余弦定理,可求出BC 的,根据相似三角形段成比例,可求出 B 2B1的,同理,可求得段【解答】解:∵ AB=AC=1 ,∠ ABC=72 °, BB 1平分∠ ABC 交 AC 于 B 1,∴△ BCB 1和△B 2B1B 是等腰三角形,∵ B 1作 B1B 2∥BC 交 AB 于 B2,∴= ,2 2 22AB ?ACcos36 °,∵BC =AB +ACB2n﹣1B 2n的度.∴BC=,设 B 2B 1 是 x ,则 B 2B 是 x .∴= ,∴x=即: B 1B 2=.同理可求出 B 2n ﹣ 1B 2n =( n ﹣ 2) .故答案为:,()n ﹣ 2.【点评】 本题考查相似三角形的判定和性质,关键是知道相似三角形的对应线段成比例,以及余弦定理求出 BC 的长,找出规律求出值.三、解答题(本题共30 分,每小题 5 分)13.用配方法解方程:.【考点】 解一元二次方程 -配方法.【分析】 先把常数项﹣ 3 移项后;然后等上的两边同时乘以 2 把二次项的系数化为 1;最后左右两边同时加上一次项系数﹣ 4 的一半的平方. 【解答】 解:由原方程,得x 2﹣ 2x=3 ,等上的两边同时乘以 2,得2x ﹣4x=6 ,方程两边同时加上一次项系数一半的平方,得 x 2﹣4x+4=10 ,配方得( x ﹣ 2) 2=10. ∴ , ∴,.【点评】 本题考查了解一元二次方程﹣﹣配方法. 配方法的一般步骤:( 1)把常数项移到等号的右边;( 2)把二次项的系数化为 1;( 3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为 1,一次项的系数是 2 的倍数.14.计算: 3sin30°﹣ 2cos 45°+2tan60°cos30°.【考点】 特殊角的三角函数值. 【分析】 将特殊角的三角函数值代入求解. 【解答】 解:原式 =3× ﹣ ×( )2+2× ×= ﹣.【点评】 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.15.如图, △ ABC 与 △ADE 都是等腰直角三角形,且∠ BAC= ∠ DAE=90 °,请找出一条与线段 CE 相等的线段(以图中已知点的端点),画出这条线段并给出证明.【考点】 全等三角形的判定与性质;等腰直角三角形.【分析】 连接 BD ,则 BD=CE ,证明 △AEC ≌△ ADB 即可. 【解答】 解:连接 BD ,则 BD=CE ;理由:∵△ ABC 与 △ADE 都是等腰直角三角形,∴ A B=AC , AE=AD ,∵∠ BAC= ∠DAE=90 °, ∴∠ BAD= ∠ CAE ,在△ AEC 和 △ADB 中,,∴△ AEC ≌△ ADB ( SAS ), ∴BD=CE .【点评】 本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解决问题的关键.16.已知 m 是方程 x 2﹣ x ﹣3=0 的根,求代数式( 1+ ) ?( m ﹣ 3)的值.【考点】 分式的化简求值;一元二次方程的解.m 是方程 x 2﹣ x ﹣ 3=0 的根【分析】 先根据分式混合运算的法则把原式进行化简,再根据【解答】解:原式 =?(m﹣ 3)=,2∵m 是方程 x ﹣ x﹣ 3=0 的根,∴原式 ==1.【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.17.如图,半径为 5 的⊙ O 中, AB 是直径,弦 BC=8 ,OD ⊥ AB 交 BC 于 D ,求 CD 的长及△ OCD 的面积.【考点】垂径定理;勾股定理.【分析】过点 O 作 OE⊥ CD 于点 E,根据相似三角形的判定定理可得出△ ODE∽△ BOE,再由相似三角形的对应边成比例可求出OD 的长,由勾股定理得出DE 的长,进而得出CD 的长,根据三角形的面积公式即可得出结论.【解答】解:过点 O 作 OE⊥CD 于点 E,∵B C=8 ,∴C E=BE=4 ,OE=3 .∵OD ⊥AB ,∴∠ BEO= ∠OED=90 °,∵∠ ODE+ ∠ OBE=90 °,∠ ODE+ ∠DOE=90 °,∴∠ DOE= ∠ OBE ,∴△ ODE∽△ BDO ,∴=,即=,解得DE=,∴CD=CE ﹣ DE=4 ﹣=,∴S△OCD= CD ?OE=× ×3=.【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.18.列方程或方程组解应用题:某酒店有三人间、双人间的客房,三人间每天每间150 元,双人间每天每间 140 元,为了吸引游客,实行团体入住五折优惠措施,一个50 人的旅游团优惠期间到该酒店入住,住了一些三人间和双人间客房,若每间客房正好住满且一天共花去住宿费1510 元,则该旅行团住了三人间和双人间客房各多少间?【考点】二元一次方程组的应用.【分析】本题中的等量关系有两个:三人间所住人数+二人间所住人数 =50 人;三人间费用×0.5+二人间费用×0.5=1510 ,据此可列方程组求解.【解答】解:设三人间和双人间客房各x 间、 y 间,根据题意,得,解得.答:该旅行团住了三人间和双人间客房各8 间、 13 间.【点评】本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出 2 个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.四、解答题(本题共 20 分,每小题 5 分)19.如图,直线 y=﹣ 2x+1 分别交 x 轴, y 轴于点 A , B ,交反比例函数y= 的图象于点C, CB : BA=2 : 1.(1)求反比例函数 y= 的解析式;(2)若点 P 在 y 轴上且以点 B, C,P 为顶点的三角形与△ AOB 相似,直接写出点 P 的坐标.【考点】反比例函数与一次函数的交点问题.【分析】(1)由直线的解析式求得 A 、 B 的坐标,进而根据CB :BA=2 : 1 求得 C 的纵坐标,将 C 坐标代入直线y= ﹣ 2x+1 中求出横坐标,代入反比例函数y=,确定出反比例解析式;(2)分两种情况分别讨论即可求得.【解答】解:( 1)∵直线y=﹣ 2x+1 分别交 x 轴, y 轴于点 A , B ,∴A (,0),B(0,1),∵CB : BA=2 : 1,∴=,作CD⊥ x 轴于 D ,则 CD ∥OB ,∴△ ACD ∽△ ABO ,∴= ,∴= ,∴C D=3 ,把y=3 代入 y= ﹣ 2x+1,解得 x= ﹣1,∴C(﹣ 1, 3),代入 y=得,3=,∴k= ﹣ 3,∴反比例函数y=的解析式为y=﹣;(2)当△CPB ∽△ AOB 时,则= ,即 = ,∴B P=2 ,∴O P=OB+BP=1+2=3 ,∴P( 0, 3);当△ PCB∽△ AOB 时,则= ,∵OA=,OB=1,∴AB==,∵CB : BA=2 : 1,∴CB=,∴=,∴P B= ,∴O P=PB+0B= +1= ,∴P( 0,);故 P 的坐标为( 0, 3)或( 0,).【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,一次函数与坐标轴的交点,三角形相似的性质,熟练掌握待定系数法是解本题的关键.20.如图,已知,在△ ABC 中,∠ ABC=90 °, BC 为⊙ O 的直径, AC 与⊙ O 交于点 D,点E 为 AB 的中点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.(1)求证: ED 是⊙ O 的切线;(2)如果 CF=1, CP=2, sinA= ,求⊙ O 的直径 BC .【考点】 切线的判定;相似三角形的判定与性质;解直角三角形. 【专题】 几何综合题.【分析】 (1)连接 OD ,证 OD ⊥ DE 即可.易证∠ ADB=90 °,又点 E 为 AB 的中点,得 DE=EB .根据等腰三角形性质可证 ∠ODE= ∠ OBE=90 °,得证;(2)可证∠ A= ∠ DBC ,所以要求 BC 需先求 DC .结合已知条件,证明 △ PDC 与 △FPC 相似可求 CD ,得解.【解答】 (1)证明:连接 OD .∵BC 为直径,∴△ BDC 为直角三角形. 在 Rt △ ADB 中,E 为 AB 中点,∴ BE=DE , ∴∠ EBD= ∠ EDB .又∵ OB=OD ,∴∠ OBD= ∠ ODB ,∵∠ OBD+ ∠ ABD=90 °,∴∠ ODB+ ∠ EDB=90 °. ∴ED 是⊙ O 的切线.(2)解:∵ PF ⊥BC ,∴∠ FPC=90°﹣∠ BCP (直角三角形的两个锐角互余).∵∠ PDC=90 °﹣∠ PDB (直径所对的圆周角是直角),∠ PDB= ∠ BCP (同弧所对的圆周角相等),∴∠ FPC=∠ PDC (等量代换). 又∵∠ PCF 是公共角, ∴△ PCF ∽△ DCP . ∴= ,则 PC 2=CF?CD (相似三角形的对应边成比例). ∵CF=1 , CP=2,∴CD=4 .可知 sin ∠DBC=sinA=,∴= ,即 = ,∴直径 BC=5 .【点评】此题考查了切线的判定、相似三角形的判定和性质、三角函数等知识点,综合性较强,难度偏上.21.据报道,历经一年半的调查研究,PM 2.5 源解析已经通过专家论证.各种调查显示,机动车成为 PM 2.5 的最大来源,一辆车一天行驶 20 千米,那么这辆车每天至少就要向大气里排放 0035 千克污染物.以下是相关的统计图、表:年全年空气质量等级天数统计表空气质量等级优良轻度污中度污重度污严重污染染染染天数(天)41 135 84 47 45 13(1)请根据所给信息补全扇形统计图;(2)请你根据“年全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到 0.01)(3)小明是社区环保志愿者,他和同学们调查了本社区的100 辆机动车,了解到其中每天出行超过 20 千米的有 40 辆.已知年机动车保有量已突破 520 万辆,请你通过计算,估计年一天中出行超过 20 千米的机动车至少要向大气里排放多少千克污染物?【考点】扇形统计图;用样本估计总体;统计表;列表法与树状图法.【分析】(1)用单位 1 减去其他原因所占的百分比即可确定答案;(2)用重度污染和严重污染的天数除以所有的天数即可确定出现的频率;(3)用样本估计总体即可.【解答】解:( 1) 31.1;(2)≈0.16.该年度重度污染和严重污染出现的频率共是0.16.(3)=7 280 0,20 千米的机动车至少要向大气里排放72800 千克污染物.估计年一天中出行超过【点评】本题考查了扇形统计图、用样本估计总体等知识,解题的关键是能够从统计图中整理出进一步解题的有关信息.22.如图 1,给定锐角三角形ABC ,小明希望画正方形 DEFG ,使 D, E 位于边 BC 上,F, G 分别位于边 AC , AB 上,他发现直接画图比较困难,于是他先画了一个正方形HIJK ,是的 H, I ,位于射线 BC 上, K 位于射线 BA 上,而不需要求 J 必须位于 AC上.这是他发现可以将正方形HIJK 通过放大或缩小得到满足要求的正方形DEFG .阅读以上材料,回答小明接下来研究的以下问题:(1)如图 2,给定锐角三角形ABC ,画出所有长宽比为2: 1 的长方形 DEFG ,使 D , E 位于边 BC 上, F, G 分别位于边 AC , AB 上.(2)已知三角形 ABC 的面积为 36, BC=12 ,在第( 1)问的条件下,求长方形DEFG 的面积.【考点】位似变换.【分析】(1)如图 2,先画长方形 HIJK ,使得 HI=2HK ,并且 H , I 位于射线 BC 上, K 位于射线 BA 上,连结 BJ 并延长交 AC 于点 F,再将长方形 HIJK 通过放大可得到满足要求的长方形DEFG ;如备用图,先画长方形HIJK ,使得 HK=2HI ,并且 H , I 位于射线BC 上, K 位于射线BA 上,连结BJ 并延长交AC 于点 F,再将长方形HIJK 通过放大可得到满足要求的长方形DEFG ;(2)作△ABC 的高 AM ,交 GF 于 N .由三角形ABC 的面积为36,求出 AM=6 .再设AN=x ,由 GF∥BC ,得出△ AGF ∽△ ABC ,根据相似三角形对应高的比等于相似比列出比例式 = ,由此求出 x 的值,进而求解即可.【解答】解:( 1)如图 2 与备用图1,长方形DEFG 即为所求作的图形;(2)在长方形 DEFG 中,如果 DE=2DG ,如备用图 2,作△ ABC 的高 AM ,交 GF 于 N .∵三角形 ABC 的面积 = BC ?AM= ×12AM=36 ,∴A M=6 .设AN=x ,则 MN=6 ﹣ x, DG=MN=6 ﹣x, DE=GF=2 ( 6﹣x) =12﹣2x.∵GF∥ BC ,∴△ AGF ∽△ ABC ,∴= ,∴= ,解得 x=3 ,∴D G=6 ﹣ x=3, DE=2DG=6 ,∴长方形 DEFG 的面积 =6×3=18;在长方形 DEFG 中,如果 DG=2DE ,同理求出 x= ,∴DG=6 ﹣ x=,DE= DG= ,∴长方形 DEFG 的面积 =× =.故长方形 DEFG 的面积为 18 或.【点评】 本题考查了位似变换,相似三角形的判定与性质,根据题意作出符合要求的长方形 DEFG 是解题的关键.五、解答题(本题共 22 分,第 23 题 7 分,第 24 题 7 分,第 25 题 8 分)23.已知关于 x 的二次函数 y 1=x 2﹣( m+3) x+m+2 , y 2=﹣ x 2 +bx+c .(1)求证:方程 x 2﹣( m+3 ) x+m+2=0 必有实根; (2)若 m 为整数, y 1 的图象与 x 轴有一个交点的横坐标a 满足 5< a < 7,求 m 的值; (3)在第( 2)问的条件下,小明利用函数图象解关于 x 的不等式 y 1 <y 2,正确解得该不等式的解集为 3< x < 4,求 y 2 的解析式.【考点】 二次函数与不等式(组);抛物线与 x 轴的交点.【分析】 (1)利用根的判别式即可得出结论;(2)根据 y 1 的图象与 x 轴有一个交点的横坐标 a 满足 5<a < 7 可知当 x=5 时, y 1< 0,当x=7 时, y 1 >0 求出 m 的取值范围,再由 m 为整数即可求出 m 的值; (3)先求出当 x=3 ,x=4 时 y 1 的值,再由 y 2 也经过此点即可得出结论. 【解答】 解:(221)∵△ =[ ﹣( m+3)] ﹣ 4( m+2) =( m+1) ≥0,∴方程 x 2﹣( m+3) x+m+2=0 必有实根; (2)∵ y 1 的图象与 x 轴有一个交点的横坐标 a 满足 5< a < 7,且抛物线开口向上,∴f (5)< 0, f (7)> 0,∴,解得 3< m < 5.∵m 为整数, ∴ m =4 ;(3)∵由( 2)知, m=4,22∴关于 x 的二次函数 y 1=x ﹣( m+3) x+m+2 可化为 y 1=x ﹣ 7x+6 ,2∵二次函数 y 2=﹣ x + bx+c 经过( 3,﹣ 6),( 4,﹣ 6), ∴,解得,∴y 2 的解析式为 2﹣ 72.y 2=﹣ x +25x【点评】本题考查的是二次函数与不等式组,能根据题意画出图形,利用数形结合求解是解答此题的关键.24.过正方形 ABCD 的顶点 A 任作一条直线 l ( l 不过点 B,C, D),过点 B, C,D 作 l 的垂线段 BF ,CG,DH .(1)如图 1,若直线 l 过线段 BC 的中点 E,则 BF : CG: DH=1 : 1: 2.(2)如图 2,若直线 l 与线段 BC 相交于点 E,则 BF , CG, DH 满足等量关系式DH=BF+CG ,请证明你的猜想;(3)如果直线l 与线段 CB 的延长线相交,直接写出BF, CG, DH 满足的等量关系式BF=DH+CG ,在直线l 旋转一周的过程中(l 不过点 B , C, D),直接写出y=的取值范围1< y≤2.【考点】四边形综合题.【分析】(1)如图 1 所示:设AB=2a ,根据题意得:BE=a ,由勾股定理可求得AE= a,由面积法可求得 BF 和 HD 的长度,然后再证明△ BFE≌△ CGE,得到BF=CG ,从而可求得答案;(2)如图 2 所示:先根据同角的余角相等,证明∠ADH= ∠ FBE= ∠ GCE,由锐角三角函数的定义可得到,然后利用比例的性质对比例式进行变形可证得:,由 AD=BC ,于是可得到DH=BF+CG ;(3)如图 3 所示:先证明∠ABF= ∠ HDE= ∠ GCE,由锐角三角函数的定义可得到,然后利用比例的性质对比例式进行变形可证得,由 AB=DC 于是得到 BF=DH+CG ;如图 4、 5 所示可求得 BF+CG+DH 的最大值为 2BD ,最小值为 BD ,从而可求得 y 的范围.【解答】解:( 1)如图 1 所示:连接ED .设AB=2a ,根据题意得: BE=a .在 Rt△ ABE 中, AE=,∵,即:,∴BF=.在△ BFE 和△ CGE 中,,∴△ BFE ≌△ CGE.∴BF=CG .∵,即,∴HD=.∴B F : CG: DH=1 :1:2.(2) DH=BF+CG .理由:如图 2 所示:∵∠ ADH+ ∠ DAH=90 °,∠ BAH+ ∠DAH=90 °,∴∠ ADH= ∠ BAH .同理∠ FBE= ∠BAH .∴∠ ADH= ∠ FBE .∵B F ⊥ AE , GC⊥AE ,∴BF ∥ GC.∴∠ FBE= ∠ GCE.∴∠ ADH= ∠ FBE= ∠GCE.∴.由可知:,∴,即.∴.∴.∵AD=BC ,∴DH=BF+CG .(3) BF=DH+CG .理由:如图 3 所示:根据题意可知:∠ABF= ∠ HDE= ∠ GCE.∴.∴.∴,即.∴.∴.∵AB=DC ,∴BF=DH+CG .如图 4 所示:当直线经过点 C 时, BF+DH+CG 有最小值,最小值=BD ,∴y=1 .如图 5 所示:BF+DH+CG 有最大值,最小值=2AC=2BD ,∴y=2 .∵直线 l 不经过点 B 、C、 D,∴y 的取值范围是:1<y≤2.。
2019-2020学年北京人大附中九年级(上)月考数学试卷(12月份)副标题题号一二三四总分得分一、选择题(本大题共8小题,共24.0分)1.中国传统扇文化有着深厚的底蕴,下列扇面图形是中心对称图形的是()A. B.C. D.2.方程x2−x=0的解是()A. x=0B. x=1C. x1=0,x2=−1D. x1=0,x2=13.有一个可以自由转动且质地均匀的转盘,被分成6 个大小相同的扇形.在转盘的适当地方涂上灰色,未涂色部分为白色.为了使转动的转盘停止时,指针指向灰色的,则下列各图中涂色方案正确的是()概率为23A. B. C. D.4.下列关于二次函数y=2x2的说法正确的是()A. 它的图象经过点(−1,−2)B. 当x<0时,y随x的增大而减小C. 它的图象的对称轴是直线x=2D. 当x=0时,y有最大值为05.如图,△ABC∽△A′B′C′,AD和A′D′分别是△ABC和△A′B′C′的高,若AD=2,A′D′=3,则△ABC与△A′B′C′的面积的比为()A. 4:9B. 9:4C. 2:3D. 3:26.如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段AB放大后得到线段CD.若点A(1,2),B(2,0),D(5,0),则点A的对应点C的坐标是(),5) C. (3,5) D. (3,6)A. (2,5)B. (527.如图,数轴上有A、B、C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外,⊙O内,⊙O上,则原点O的位置应该在()A. 点A与点B之间靠近A点B. 点A与点B之间靠近B点C. 点B与点C之间靠近B点D. 点B与点C之间靠近C点8.如图,AB是半圆O的直径,按以下步骤作图:(1)分别以A,B为圆心,大于AO长为半径作弧,两弧交于点P,连接OP与半圆交于点C;AC长为半径作弧,两(2)分别以A,C为圆心,大于12弧交于点Q,连接OQ与半圆交于点D;(3)连接AD,BD,BC,BD与OC交于点E.根据以上作图过程及所作图形,下列结论:①BD平分∠ABC;②BC//OD;③CE=OE;④AD2=OD⋅CE;所有正确结论的序号是()A. ①②B. ①④C. ②③D. ①②④二、填空题(本大题共8小题,共24.0分)9.如图,△ABC中,点D,E分别在AB,AC边上,DE//BC,若10.如图,点A、B、C、D、O都在方格纸上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为______.11.已知反比例函数y=m−2x,当x>0时,y随x增大而减小,则m的取值范围是______.12.若一个扇形的半径为3,圆心角是120°,则它的面积是______.13.小宇调查了初一年级三个班学生的身高,并进行了统计,列出如频数分布表:若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示,不考虑其他因素的影响,则______(填“1班”,“2班”或“3班”)的可供挑选的空间最大.身高/厘米频数班级150≤x<155155≤x<160160≤x<165165≤x<170170≤x<175合计1班181214540 2班1015103240 3班51010874014.如图,在平面直角坐标系xOy中,函数y=2x(x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,连接OA,OB,则△OAC与△OBD的面积之和为______.15.为测量附中国旗杆的高度,小宇的测量方法如下:如图,将直角三角形硬纸板△DEF的斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上.测得DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.6米,到旗杆的水平距离DC=18米,按此方法,可计算出旗杆的高度为______米.16.如图,在Rt△ABC中,∠C=90°,记x=AC,y=BC−AC,在平面直角坐标系xOy中,定义(x,y)为这个直角三角形的坐标,Rt△ABC为点(x,y)对应的直角三角形.有下列结论:①在x轴正半轴上的任意点(x,y)对应的直角三角形均满足AB=√2BC;(x>0)的图象上存在两点边P,Q,使得它们对应的直角三角形②在函数y=2019x相似;③对于函y=(x−2020)2−1(x>0)的图象上的任意一点P,都存在该函数图象上的另一点Q,使得这两个点对应的直角三角形相似;④在函数y=−2x+2020(x>0)的图象上存在无数对点P,Q(P与Q不重合),使得它们对应的直角三角形全等.所有正确结论的序号是______.三、计算题(本大题共1小题,共6.0分)17.如图,⊙O是△ABC的外接圆,直径BD与AC交于点E,过点D作⊙O的切线,与BC的延长线交于点F.(1)求证:∠F=∠BAC;(2)若DF//AC,若AB=8,CF=2,求AC的长.四、解答题(本大题共11小题,共88.0分)18.解方程:x2−2x=2(x+1).19.如图,已知∠B=∠C=90°,点E在BC上,且满足AB=4,BE=2,CE=6,CD=3,求证:AE⊥DE.20.已知二次函数y=x2−4x+3.(1)用配方法将y=x2−4x+3化成y=a(x−ℎ)2+k的形式;(2)在平面直角坐标系xOy中画出该函数的图象;(3)当0≤x≤3时,y的取值范围是______.21.如图,四边形ABCD内接于⊙O,OC=2,AC=2√2(1)求点O到AC的距离;(2)求∠ADC的度数.22.某市计划建设一项水利工程,运输公司接到任务后,计划每天运输土方2000m3,共计50天运完,但由于受到各种因素的影响,实际平均每天运输土方vm3,共计t 天运输完成.(1)请直接写出v关于t的函数关系式;(2)为了给后续工程节省出时间,这批土方需要在40天内运输完成,求实际平均每天至少需要比原计划增加多少土方运输量?x2+bx+c=023.已知关于x的一元二次方程14(1)c=2b−1时,求证:方程一定有两个实数根.(2)有甲、乙两个不透明的布袋,甲袋中装有3个除数字外完全相同的小球,分别标有数字1,2,3,乙袋中装有4个除数字外完全相同的小球,分别标有数字1,2,3,4,从甲袋中随机抽取一个小球,记录标有的数字为b,从乙袋中随机抽取一个小球,记录标有的数字为c,利用列表法或者树状图,x2+bx+c=0两个相等的实数根的概率.求b、c的值使方程14(x>0)的24.如图,在平面直角坐标系xOy中,直线l:y=kx−1(k≠0)与函数y=mx 图象交于点A(3,2).(1)求k,m的值;(2)将直线l沿y轴向上平移t(t>0)个单位后,所得直线与x轴,y轴分别交于点P,(x>0)的图象交于点C.Q,与函数y=mx①当t=2时,求线段QC的长.<3,结合函数图象,直接写出t的取值范围.②若2<QCPQ25.如图,在弧AB和弦AB所组成的图形中,P是弦AB上一动点,过点P作弦AB的垂线,交弧AB于点C,连接AC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,A,C两点间的距离为y2cm.小宇根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小宇的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:x/cmx/cm0123456y1/cm0 2.24 2.83 3.00 2.83 2.240y2/cm0 2.45 3.46 4.24______ 5.486(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;(3)结合函数图象,解决问题:当△APC有一个角是60°时,AP的长度约为______26.在平面直角坐标系xOy中,抛物线y=x2−2ax+a2−a+4的顶点为A,点B,C为直线y=3上的两个动点(点B在点C的左侧),且BC=3.(1)求点A的坐标(用含a的代数式表示);(2)若△ABC是以BC为直角边的等腰直角三角形,求抛物线的解析式;(3)过点A作x轴的垂线,交直线y=3于点D,点D恰好是线段BC三等分点且满足BC=3BD,若抛物线与线段BC只有一个公共点,结合函数的图象,直接写出a 的取值范围.27.如图,在Rt△ABC中,∠ACB=90°,点C关于直线AB的对称点为D,连接BD,CD,过点B作BE//AC交直线AD于点E.(1)依题意补全图形;(2)找出一个图中与△CDB相似的三角形,并证明;(3)延长BD交直线AC于点F,过点F作FH//AE交直线BE于点H,请补全图形,猜想BC,CF,BH之间的数量关系并证明.28.新定义:在平面直角坐标系xOy中,若几何图形G与⊙A有公共点,则称几何图形G的叫⊙A的关联图形,特别地,若⊙A的关联图形G为直线,则称该直线为⊙A 的关联直线.如图,∠M为⊙A的关联图形,直线l为⊙A的关联直线.(1)已知⊙O是以原点为圆心,2为半径的圆,下列图形:①直线y=2x+2;②直线y=−x+3;③双曲线y=2,是⊙O的关联图形的是x______(请直接写出正确的序号).(2)如图1,⊙T的圆心为T(1,0),半径为1,直线l:y=−x+b与x轴交于点N,若直线l是⊙T的关联直线,求点N的横坐标的取值范围.(3)如图2,已知点B(0,2),C(2,0),D(0,−2),⊙I经过点C,⊙I的关联直线HB经过点B,与⊙I的一个交点为P;⊙I的关联直线HD经过点D,与⊙I的一个交点为Q;直线HB,HD交于点H,若线段PQ在直线x=6上且恰为⊙I的直径,请直接写出点H横坐标h的取值范围.答案和解析1.【答案】C【解析】解:A、不是中心对称图形,故此选项错误;B、不是中心对称图形,故此选项错误;C、是中心对称图形,故此选项正确;D、不是中心对称图形,故此选项错误;故选:C.根据中心对称图形的概念求解.此题主要考查了中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180度后两部分重合.2.【答案】D【解析】解:x(x−1)=0,x=0或x−1=0,所以x1=0,x2=1.故选:D.先把方程左边分解,这样把原方程化为x=0或x−1=0,然后解一次方程即可.本题考查了解一元二次方程−因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).3.【答案】C,故选项错误;【解析】解:A、指针指向灰色的概率为2÷6=13B、指针指向灰色的概率为3÷6=1,故选项错误;2C、指针指向灰色的概率为4÷6=2,故选项正确;3D、指针指向灰色的概率为5÷6=5,故选项错误.6故选:C.指针指向灰色区域的概率就是灰色区域的面积与总面积的比值,计算面积比即可.本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.4.【答案】B【解析】解:二次函数y =2x 2,当x =−1时,y =2,故它的图象不经过点(−1,−2),故A 选项不合题意;当x <0时,y 随x 的增大而减小,故选项B 正确; 它的图象的对称轴是直线 y 轴,故C 选项不合题意; 当x =0时,y 有最小值为0,故D 选项不合题意; 故选:B .直接利用二次函数的性质分别判断得出答案.此题主要考查了二次函数的性质,正确掌握二次函数的增减性是解题关键.5.【答案】A【解析】解:∵△ABC∽△A′B′C′,AD 和A′D′分别是△ABC 和△A′B′C′的高,AD =2,A′D′=3,∴ABA′B′=ADA′D′=23,∴△ABC 与△A′B′C′的面积的比=(23)2=49, 故选:A .根据相似三角形对应高的比等于相似比求出相似比,根据相似三角形面积的比等于相似比的平方解答.本题考查的是相似三角形的性质,相似三角形面积的比等于相似比的平方、相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.6.【答案】B【解析】 【分析】此题主要考查了位似变换,正确得出对应点的关系是解题关键.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或−k.利用位似图形的性质得出位似比,进而得出对应点坐标的关系.【解答】解:∵以原点O为位似中心,把线段AB放大后得到线段CD,且B(2,0),D(5,0),∴OBOD =25,∵A(1,2),∴C(52,5).故选B.7.【答案】C【解析】解:如图,观察图象可知,原点O的位置应该在点B与点C之间靠近B点,故选:C.画出图象,利用图象法即可解决问题;本题考查点与圆的位置关系,解题的关键是理解题意,学会利用图象法解决问题.8.【答案】D【解析】解:由作图可知,OP垂直平分线段AB,OQ平分∠AOC,故①正确,∴OP⊥AB,∴∠AOC=∠BOC=90°,∴∠AOD=12∠AOC=45°,∵OB=OC,∴∠OBC=45°,∴∠AOD=∠OBC=45°,∴OD//BC,故②正确,∴ODBC =OEEC<1,∴OE<EC,故③错误,连接CD.∵∠DCE=∠DCO,∠CDE=∠COD=45°,∴△DCE∽△OCD,∴CDOC =CECD,∴CD2=OD⋅CE,∵∠AOD=∠DOC,∴AD⏜=CD⏜,∴AD=CD,∴AD2=OD⋅CE,故④正确,故选:D.由作图可知,OP垂直平分线段AB,OQ平分∠AOC,利用平行线的判定,相似三角形的性质一一判断即可.本题考查相似三角形的判定和性质,圆周角定理,平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.9.【答案】2.5【解析】解:∵DE//BC,∴△ADE∽△ABC,∴DE:BC=AD:AB,∵AD=2,DB=3,∴AB=AD+BD=5,∴1:BC=2:5,∴BC=2.5,故答案为:2.5.首先由DE//BC,可证得△ADE∽△ABC,进而可根据相似三角形得到的比例线段求得BC的长.本题考查了相似三角形的性质和判定,关键是求出相似后得出比例式,题目比较典型,难度适中.10.【答案】135°【解析】解:∵△COD是由△AOB绕点O按逆时针方向旋转而得,∴∠AOC为旋转角,∵∠AOB=45°,∴∠AOC=135°,即旋转角为135°.故答案为:135°.利用旋转的性质得到∠AOC为旋转角,然后利用∠AOB=45°得到∠AOC的度数即可.本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.11.【答案】m>2【解析】【分析】本题考查了反比例函数的性质,根据反比例函数的性质找出m−2>0是解题的关键.,当x>0时,y随x增大而减小,可得出m−2>0,解之即可根据反比例函数y=m−2x得出m的取值范围.【解答】,当x>0时,y随x增大而减小,解:∵反比例函数y=m−2x∴m−2>0,解得:m>2.故答案为m>2.12.【答案】3π=3π,【解析】解:扇形的面积=120⋅⋅π⋅32360故答案为3π.利用扇形的面积公式计算即可..本题考查扇形的面积,解题的关键是记住扇形的面积公式S=nπr236013.【答案】1班【解析】解:身高在160cm和170cm之间同学人数:一班26人,二班13人,三班18人,因此可挑选空间最大的是一班,故答案为:1班.根据各个班身高在160cm和170cm之间同学的人数,进行判断即可.考查频数分布表的表示方法,从表格中获取数据和数据之间的关系是正确判断的前提.14.【答案】2【解析】解:∵函数y=2x(x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,∴S△OAC=S△OBD=12×2=1,∴S△OAC+S△OBD=1+1=2.故答案为2.根据反比例函数比例系数k的几何意义可得S△OAC=S△OBD=12×2=1,再相加即可.本题考查了反比例函数比例系数k的几何意义:过反比例函数图象上的点向x轴或y轴作垂线,这一点和垂足、原点组成的三角形的面积等于12|k|.15.【答案】10.6【解析】解:∵CD⊥AB,△DEF为直角三角形,∴∠DEF=∠ACD,∵∠ADC=∠FDE,∴△ACD∽△FED,∴DECD =EFAC,∵DE=0.5米,EF=0.25米,DC=18米,∴0.518=0.25AC,∴AC=9米,∵DG=1.6米,∴BC=1.6米,∴AB=10.6米,故答案为:10.6.根据题意证出△ACD∽△FED,进而利用相似三角形的性质得出AC的长,即可得出答案.此题主要考查了相似三角形的应用;由三角形相似得出对应边成比例是解题关键.16.【答案】①③④【解析】解:①∵在x轴正半轴上的任意点(x,y),∴y=0,∴AC=BC,∴AB=√2BC;②设P({x1,2019 x1),Q(x2,2019x2),则对应的直角三角形的直角边分别为x1,x1+2019 x1;x2,x2+2019x2,若两个三角形相似,则有x1x1+2019x1=x2x2+2019x2,∴x22=x12,∵x>0,∴x1=x2,∴不存在两点边P,Q,使得它们对应的直角三角形相似;③设P(x1,(x1−2020)2−1),Q(x2,(x2−2020)2−1),则对应的直角三角形的直角边分别为x1+(x1−2020)2−1,x1;x2,x2+(x2−2020)2−1,若两个三角形相似,则有x1(x1−2020)2−1=x2(x2−2020)2−1,∴(x1−x2)(x1x2+1−20202)=0,∵x>0,∴x1x2+1=20202,∴图象上的任意一点P,都存在该函数图象上的另一点Q,使得这两个点对应的直角三角形相似;④设P(x1,−2x1+2020),Q(x2,−2x2+2020),则对应的直角三角形的直角边分别为x1,−x1+2020;x2,−x2+2020,若两个三角形全等,则有x1=−x2+2020,x2=−x1+2020,∴x2+x1=2020,∵x>0,∴图象上存在无数对点P,Q,使得它们对应的直角三角形全等;故答案为①③④.①在x轴正半轴上的任意点(x,y),则y=0,所以AC=BC,由勾股定理可得AB=√2BC;②设P({x1,2019 x1),Q(x2,2019x2),则对应的直角三角形的直角边分别为x1,x1+2019 x1;x2,x2+2019x2,若两个三角形相似,则有x1x1+2019x1=x2x2+2019x2,可得x22=x12,当x>0时x1=x2;③设P(x1,(x1−2020)2−1),Q(x2,(x2−2020)2−1),则对应的直角三角形的直角边分别为x1+(x1−2020)2−1,x1;x2,x2+(x2−2020)2−1,若两个三角形相似,则有x1(x1−2020)2−1=x2(x2−2020)2−1,(x1−x2)(x1x2+1−20202)=0,由条件可得x1x2+1=20202;④设P(x1,−2x1+2020),Q(x2,−2x2+2020),则对应的直角三角形的直角边分别为x1,−x1+2020;x2,−x2+2020,若两个三角形全等,则有x1=−x2+2020,可得x2+x1=2020.本题考查函数的性质,新定义,三角形性质;能够理解题意,将问题转化为直角三角形相似与全等,利用相似与全等的关系结合直角三角形的性列出正确的等式,再能正确求解方程是解题的关键.17.【答案】(1)证明:∵DF是⊙O的切线,∴OD⊥DF,∴∠ODF=90°,∴∠F+∠DBC=90°,∵BD是⊙O的直径,∴∠BAD=90°,∴∠BAC+∠DAC=90°,∵∠DBC=∠DAC,∴∠BAC=∠F(2)解:连接CD,∵DF//AC,∠ODF=90°,∴∠BEC=∠ODF=90°,∴直径BD⊥AC于E,∴AE=CE=12AC,∴AB=BC,∵AB=8,∴BC=8,∵BD是⊙O的直径,∴∠BCD=90°,∴∠DBC+∠BDC=90°,∵∠DBC+∠F=90°,∴∠BDC=∠F,∵∠BCD=∠FCD=90°,∴△BCD∽△DCF,∴BCDC =DCCF,∵BC=8,CF=2,∴DC=4,∴BD=√BC2+CD2=4√5.∵在△BCD中,S△BCD=12BC⋅CD=12BD⋅CE,∴CE=85√5,∴AC=2CE=165√5.【解析】(1)证∠F+∠DBC=90°,可得∠BAC+∠DAC=90°,又∠DBC=∠DAC,则∠BAC=∠F,结论得证;(2)连接CD,证明△BCD∽△DCF,可得BCDC =DCCF,求出DC=4,BD=4√5,由三角形面积可得出CE,则AC可求出.本题考查了相似三角形的性质及判定,切线的性质,等腰三角形的判定与性质,勾股定理,三角形的面积等知识,解答时运用好切线的性质求解是解答本题的关键.18.【答案】解:整理得x2−4x=2,x2−4x+4=2+4,即(x−2)2=6,∴x−2=±√6,∴x1=2+√6,x2=2−√6.【解析】整理得x2−4x=2,然后利用配方法求解即可.本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.19.【答案】证明:∵AB=4,BE=2,CE=6,CD=3,∴ABCE =BECD,∵∠B=∠C=90°,∴△ABE∽△ECD,∴∠A=∠CED,∵∠B=90°,∴∠A+∠AEB=90°,∴∠CED+∠AEB=90°,∴∠AED=180°−∠AEB−∠CED=90°,∴AE⊥DE.【解析】证明△ABE∽△ECD,可得∠A=∠CED,则∠CED+∠AEB=90°,可得出∠AED= 180°−∠AEB−∠CED=90°,则结论得证.本题考查的是相似三角形的判定与性质,熟知相似三角形的性质是解答此题的关键.20.【答案】(1)y=x2−4x+3=(x−2)2−1;(2)这个二次函数的图象如图:(3)−1≤y≤3【解析】解:(1)见答案;(2)见答案;(3)当0≤x≤3时,−1≤y≤3.故答案为−1≤y≤3.【分析】(1)运用配方法把一般式化为顶点式;(2)根据函数图象的画法画出二次函数图象即可;(3)运用数形结合思想解答即可.本题考查的是二次函数的三种形式、二次函数的性质,掌握配方法把一般式化为顶点式是解题的关键.21.【答案】解:(1)连接OA,作OH⊥AC于H,OA2+OC2=8,AC2=8,∴OA2+OC2=AC2,∴△AOC为等腰直角三角形,∴OH=12AC=√2,即点O到AC的距离为√2;(2)由圆周角定理得,∠B=12∠AOC=45°,∵四边形ABCD内接于⊙O,∴∠ADC=180°−45°=135°.【解析】(1)连接OA,作OH⊥AC于H,根据勾股定理的逆定理得到∠AOC=90°,根据等腰直角三角形的性质解答;(2)根据圆周角定理求出∠B,根据圆内接四边形的性质计算,得到答案.本题考查度数圆内接四边形的性质、圆周角定理、勾股定理的逆定理,掌握圆内接四边形对角互补是解题的关键.22.【答案】解:(1)由题意得:v=2000×50t =100000t;(2)当t=40时,v=10000040=2500,2500−2000=500(m3),答:实际平均每天至少需要比原计划增加500m3土方运输量.【解析】(1)根据题意得等量关系:平均每天运输土方=土方总量÷时间,然后可得v关于t的函数关系式;(2)求出当t=40时v的值,然后其计算与2000的差即可.此题主要考查了反比例函数的应用,关键是正确理解题意,找出题目中的等量关系.23.【答案】(1)证明:∵△=b2−4⋅14c=b2−c=0,∴将c=2b−1代入得:△=b2−(2b−1)=b2−2b+1=(b−1)2≥0,∴方程一定有两个实数根;(2)解:画树状图得:∵共有12种等可能的结果,若方程有两个相等的实数根,△=b2−4⋅14c=b2−c=0,∴b2=c,满足条件的结果有(1,1)和(2,4),共2种,∴P(b、c的值使方程14x2+bx+c=0两个相等的实数根的概率)=16.【解析】(1)直接利用根的判别式以及完全平方公式进而分析得出答案;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;可得2x+y=6的情况,再利用概率公式求解即可求得答案.此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.24.【答案】解:(1)将点A(3,2)的坐标分别代入y=kx−1(k≠0)与y=mx(x>0)中,得2=3k−1,2=m3,∴k=1,m=6;(2)①∵直线y=kx−1与y轴交于点(0,−1),∴当t=2时,Q(0,1).此时直线解析式为y=x+1,代入函数y=6x中,整理得,x(x+1)=6,解得x1=−3(舍去),x2=2,∴C(2,3),∴QC=√(2−0)2+(3−1)2=2√2.②如图,作CD⊥x轴于D,若QCPQ =2时,则ODOP=2,CDOQ=3,∵直线解析式系数k=1,∴OP=OQ,设OP=OQ=a,∴OD=2a,CD=3a,∴CD=62a =3a,∴3a=3a,解得a=1,∴此时t=1+1=2,若QCPQ =3时,则ODOP=3,CDOQ=4,∵直线解析式系数k=1,∴OP=OQ,设OP=OQ=a,∴OD=3a,CD=4a,∴CD=63a =2a,∴4a=2a,解得a=√22,∴此时t=1+√22,∴若2<QCPQ <3,结合函数图象,得出t的取值范围是1+√22<t<2.【解析】(1)将点A分别代入y=kx−1(k≠0)与y=mx(x>0),即可求出k、m的值;(2)①求出当t=2时直线解析式,代入函数y=6x中,整理得,x(x+1)=6,解方程求出点C的坐标,即可求出QC的长;②观察图象解答即可.本题考查了一次函数与反比例函数的交点问题,待定系数法求解析式,利用函数图象性质解决问题是本题的关键.25.【答案】4.90 1.50或4.50【解析】解:(1)利用测量法可知:当x=4时,y2=4.90.故答案为4.90.(2)函数图象如图所示:(3)函数y1与直线y=√3x的交点的横坐标为1.50,x的交点的横坐标为4.50,函数y1与直线y=√33故当△APC有一个角是60°时,AP的长度约为1.50或4.50.故答案为1.50或4.50.(1)利用测量法解决问题即可.(2)利用描点画出函数图象即可.(3)利用图象法求出函数y1与直线y=√3x,直线y=√3x的交点的横坐标即可解决问题.3本题属于圆综合题,考查了解直角三角形,勾股定理,一次函数的性质,函数的图象与性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.26.【答案】解:(1)y=x2−2ax+a2−a+4=(x−a)2+4−a,故点A(a,4−a);(2)点A所在的直线为:y=4−x,联立y=4−x与y=−x并解得:x=1,故两个直线的交点为(1,3);①当点C的坐标为:(1,3)时,则点B(−2,3),点A(−2,6),a=−2,故抛物线的表达式为:y=(x+2)2+6;②当点B的坐标为:(1,3)时,则点A(4,0),则a=4,故抛物线的表达式为:y=(x−4)2;综上,抛物线的表达式为:y=(x+2)2+6或y=(x−4)2;(3)点A(a,4−a),则点D(a,3),BC=3BD,则点B、C的坐标分别为:(a−1,3)、(a+2,3),将抛物线y=x2−2ax+a2−a+4与直线y=3联立并解得:x=a±√a−1,故点E、F的坐标分别为:(a−√a−1,3)、(a+√a−1,3),①当a=1时,点E、B、C、F的坐标分别为:(1,3)、(0,3)、(2,3)、(1,3),而点A(1,3),此时,抛物线于BC只有一个公共点;②当a>1时,当点C、F重合时,则a+√a−1=a+2,解得:a=5;当点B、E重合时,a−√a−1=a−1,解得:a=2,故2<a≤5;综上,a=1或2<a≤5.【解析】(1)y=x2−2ax+a2−a+4=(x−a)2+4−a,即可求解;(2)分当点C的坐标为:(1,3)时、点B的坐标为:(1,3)时,两种情况分别求解;(3)分a=1、a>1两种情况,分别求解即可.本题考查的是二次函数综合运用,涉及到一次函数的性质、等腰直角三角形的性质等,其中(2)、(3),都要注意分类求解,避免遗漏.27.【答案】解:(1)如图1所示:(2)与△CDB相似的三角形是△ABE,理由如下:∵点C关于直线AB的对称点为D,∴CH=DH,AB⊥CD,∴AB是CD的垂直平分线,∴AD=AC,BC=BD,且AB⊥CD,∴∠ACD=∠ADC,∠CAB=∠DAB,∠BCD=∠BDC,∠DBA=∠CBA,∵∠ACB=90°,∴∠ABC+∠CAB=90°,且∠ABC+∠BCH=90°,∠BAC+∠ACD=90°,∴∠BCD=∠BAC,∠ACD=∠ABC,∴∠DAB=∠BCD=∠BAC=∠BDC,∵AC//BE,∴∠CAB=∠ABE,∴∠CDB=∠ABE,且∠DAB=∠BCD,∴△BCD∽△EAB;(3)BH⋅FC=BC2+CF2,理由如下:如图2,∵∠ACB=90°,∴BC2+CF2=BF2,∵△BCD∽△EAB,∴∠AEB=∠CBD,∵AE//FH,∴∠H=∠AEB=∠CBD,∵AC//BE,∴∠CFB=∠FBH,∴△FCB∽△BFH,∴BHBF =BFFC,∴BF2=BH⋅FC,∴BH⋅FC=BC2+CF2.【解析】(1)由题意补全图形;(2)由轴对称的性质可得AB是CD的垂直平分线,可得AD=AC,BC=BD,由等腰三角形的性质和余角的性质,可得∠DAB=∠BCD=∠BAC=∠BDC,由平行线的性质可得∠CAB=∠ABE=∠CDB,可证△BCD∽△BAE;(3)由勾股定理可得BC2+CF2=BF2,通过证明△FCB∽△BFH,可得BHBF =BFFC,可得结论.本题是几何变换综合题,考查了轴对称的性质,线段垂直平分线的性质,等腰三角形的性质,相似三角形的判定和性质,找到正确的相似三角形是本题的关键.28.【答案】①③【解析】解:(1)由题意①③是⊙O的关联图形,故答案为①③.(2)如图1中,∵直线l1y=−x+b是⊙T的关联直线,∴直线l的临界状态是和⊙T相切的两条直线l1和l2,当临界状态为l1时,连接TM(M为切点),∴TM=1,TM⊥MB,且∠MNO=45°,∴△TMN是等腰直角三角形,∴TN=√2,OT=1,∴N(1+√2,0),把N(1+√2,0)代入y=−x+b中,得到b=1+√2,同法可得当直线l2是临界状态时,b=−√2+1,∴点N的横坐标的取值范围为−√2+1≤≤√2+1.(3)如图3−1中,当点Q在点P是上方时,连接BQ,PD交于点H,当圆心I在x轴上时,点H与点C重合,此时H(2,0),得到h的最大值为2,如图3−2中,当点P在点Q是上方时,连接BQ,PD交于点H,当圆心I在x轴上时,点H(−6,0)得到h的最小值为−6,综上所述,−6≤ℎ<0,0<ℎ≤2.(1)根据⊙A的关联图形的定义判断即可.(2)直线l的临界状态是和⊙T相切的两条直线l1和l2,求出两种特殊情形的点N的横坐标即可解决问题.(3)分两种情形:如图3−1中,当点Q在点P是上方时,连接BQ,PD交于点H,当圆心I在x轴上时,点H与点C重合,此时H(2,0),得到h的最大值为2.如图3−2中,当点P在点Q是上方时,连接BQ,PD交于点H,当圆心I在x轴上时,点H(−6,0)得到h的最小值为−6,由此即可解决问题.本题属于圆综合题,考查了⊙A的关联图形的定义,直线与圆的位置关系等知识,解题的关键是理解题意,学会寻找特殊点,特殊位置解决问题,属于中考压轴题.。
中国人民大学附属中学2016届12月月考数学试题(理科)一、选择题:(本大题共8个小题,每小题5分,共40分.在每道小题给出的四个备选答案中,只有一个是符合题目要求的,请把所选答案前的字母按规定要求涂抹在“答题纸”第1—8题的相应位置上.) (1)定积分121x dx -=⎰( B )(A )0 (B )23(C )1 (D )2(2)已知全集U R =,集合M={|R}y y x ∈,1{21,}x N x x R -=≥∈,则()U M N ⋂=ð( B )(A )[2,2]- (B )[)0,1 (C )[)2,1- (D )[1,4] (3)抛物线22x y =-的准线方程为( B )(A )12x =(B )18x = (C )18x =- (D )12x =- (4)已知正项数列{}n a 中,11=a ,22=a ,222112(2)n n n a a a n +-=+≥,则6a 等于(D )(A )16 (B )8 (C )22 (D )4 (5)若将函数()sin 24f x x π⎛⎫=+⎪⎝⎭的图像向右平移ϕ个单位,所得图像关于y 轴对称, 则ϕ的最小正值是( C ).(A )8π (B )4π(C )38π (D )2π(6)已知()f x 是定义域为R 的奇函数,当0x <时,31()(1)e x f x x e +=+-.那么函数()f x 的极值点的个数是( A )(A )2(B )3(C )4(D )5(7)某珠宝店丢了一件珍贵珠宝,以下四人中只有一人说真话,只有一人偷了珠宝. 甲:我没有偷;乙:丙是小偷;丙:丁是小偷;丁:我没有偷. 根据以上条件,可以判断偷珠宝的人是(A )(A )甲 (B ) 乙 (C )丙 (D )丁(8)在棱长为2的正方体1111ABCD A B C D -中,若点P 是棱上一点(含顶点),则满足11PA PC u u u r u u u u r?-的点P 的个数为( C )(A )6 (B )8 (C )12 (D )241C 1A 1B 1DCAP21111+2412=4PA PC PO PO PA PC PA PC C Au u u r u u u u r u u u r u u u r u u u r u u u u r u u u r u u u u r u u u r ìï=-ï拮íï-=ïïî 二、填空题:(本大题共6小题,每小题5分,共30分,请将填空题的答案写在答题纸上相应位置.)(9)函数12y x x=+的值域为_______________。
(),22,⎤⎡-∞-⋃+∞⎦⎣(10)已知点(,)P x y 的坐标满足4160404x y x y x +-≤⎧⎪+-≥⎨⎪≤⎩,O 为坐标原点,记PO 的最大值为m ,最小值为n ,则双曲线22221x y m n-=的离心率为 335 . (11)设正数a ,b 满足23log log a b =,给出下列五个结论,其中不可能...成立的结论的序号是______. ①1a b <<; ②01b a <<<; ③a b =; ④1b a <<; ⑤01a b <<<. ④⑤;(12)已知两点(10)A ,,(0)B b ,,若抛物线24y x =上存在点C 使ABC ∆为 等边三角形,则b =_________ . 5或13-(13)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图, 则截去部分体积与剩余部分体积的比值为______.51 【解析】由三视图得,在正方体1111ABCD A B C D -中,截去四面体111A A B D -,如图所示,,设正方体棱长为a ,则11133111326A A B D V a a-=⨯=,故剩余几何体体积为3331566a a a -=,所以截去部分体积与剩余部分体积的比值为51,(14)记11210011......n n n n n n n ma a a a a a a m a m a m ----=+⨯++⨯+⨯,其中n≤m ,m 、n 均为正整数,{0,1,2,...,1}(0,1,2,...,)k a m k n ∈-=且0n a ≠;O 1C 1A 1B 1DCP 正视图 左视图俯视图AD1C 1B 11(1)计算72016= ________________;699(2)设集合{}1210(,)...n n n mA m n x x a a a a a --==,则(,)A m n 中所有元素之和为________.()()1112n n n n mm m m +++--三、解答题:本大题共6小题,共80分. 解答应写出文字说明,演算步骤或证明过程.(15)(本小题满分13分)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b 2+c 2-a 2=bc . (Ⅰ)求角A 的大小;(Ⅱ)已知a=2,设函数,当x B =时,()f x 取最大值,求△ABC的面积.解:(Ⅰ)在△ABC 中,因为b 2+c 2-a 2=bc ,由余弦定理 a 2= b 2+c 2-2bc cos A 可得cos A =.(余弦定理或公式必须有一个,否则扣1分) ……3分 ∵ 0<A <π , (或写成A 是三角形内角) …………4分 ∴. ……………………5分 (Ⅱ) ………7分 , ……………………9分∵ ∴…………10分 …………11分又∵, ∴∴△ABC 为等边三角形. …………12分 ∴S=21sin 23a π= …………13分 (16)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。
某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。
该建筑物每年的能源消耗费用C (单位:万元)与隔热层厚度x (单位:cm )满足关系:C(x )=若不建隔热层,每年能源消耗费用为8万元。
设f (x )为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k 的值及f (x )的表达式。
(Ⅱ)隔热层修建多厚时,总费用f (x )达到最小,并求最小值。
2cos 2cos 2sin 3)(2xx x x f +=123A π=2cos 2cos 2sin 3)(2xx x x f +=11cos 22x x =++1sin()62x π=++A π=2(0,)B π∈62323A =3C =(010),35kx x ≤≤+(17)(本小题共14分)如图1,在Rt ABC ∆中,90C ∠=︒,36BC AC ==,.D 、E 分别是AC AB 、上的点,且//DE BC ,将ADE ∆沿DE 折起到1A DE ∆的位置,使1A D CD ⊥,如图2. (Ⅰ)求证: BC ⊥平面1A DC ;(Ⅱ)若2CD =,求BE 与平面1A BC 所成角的正弦值;(Ⅲ) 当D 点在何处时,1A B 的长度最小,并求出最小值. (Ⅰ)证明: 在△ABC 中,90,//,C DE BC AD DE ∠=︒∴⊥1A D DE ∴⊥.又11,,A D CD CD DE D A D BCDE ⊥⋂=∴⊥面.由1,.BC BCDE A D BC ⊂∴⊥面1,,BC CD CD BC C BC A DC ⊥⋂=∴⊥面. …………………………4分(Ⅱ)如图,1BC A DC ⊥∆ 90C ∠=︒以C 为原点,建立空间直角坐标系. ……………………5分1(2,0,0),(2,2,0),(0,3,0),(2,0,4)D E B A .设(,,)x y z =n 为平面1A BC 的一个法向量,因为(0,3,0),CB =u u u r1(2,0,4)CA =u u u r所以30240y x z =⎧⎨+=⎩,令2x =,得=0,=1y z -.ABCDE图1图2A 1B CDEA 1BCD Exzy所以(2,0,1)=-n 为平面1A BC 的一个法向量. ……………………7分 设BE 与平面1A BC 所成角为θ.则4sin =cos 5BE θ<⋅>==u u u rn . 所以BE 与平面1A BC 所成角的正弦值为45. …………………9分 (Ⅲ)设(,0,0)D x ,则1(,0,6)A x x -,1A B == …………………12分当=3x 时,1A B的最小值是即D 为AC 中点时, 1A B 的长度最小,最小值为 …………………14分 (18)(本小题满分13分)已知函数(),(0)1xxe f x x e =>-; (1)求函数()y f x =的图象在点(ln 2,(ln 2))f 处的切线方程;(2)函数(),(0,*)1kg x x k x =>∈N +,若()()f x g x >在定义域内恒成立,求k 的最大值。
解:(1)222(1)'()(1)(1)x x x x x x e e e e f x e e ---==--;22'(ln 2)2(21)f -==--,2(ln 2)2,21f ==-所以切线方程为22(ln 2),y x -=--即222ln 2y x =-++。
(5分)(2),11x xe k e x >-+等价于(1),1x x e x k e +<-(6分)设(1)(),1x xe x g x e +=-2(2)'(),(1)x x x e e x g x e --=-(7分)考察函数()2x h x e x =--,由'()10xh x e =->得()2x h x e x =--在()0,+∞单调递增,(8分) 又1(1)120h e =--<,2(2)220h e =-->,存在()01,2x ∈使得0()0h x =,即0'()0g x =(10分)()g x↓ 极小 ↑故()g x 极小=()00000000(1)(1)()23,411x x x x x e x e e g x x e e +-===+∈--,(12分) 所以k 的最大值为3.(13分)(19)(本小题满分14分)已知椭圆的长轴长为6,离心率为13,2F 为椭圆的右焦点. (I )求椭圆的标准方程;(II )点M 在圆228x y +=上,且M 在第一象限,过M 作圆228x y +=的切线交椭圆于P ,Q 两点,判断△2PF Q 的周长是否为定值并说明理由.解:(I )根据已知,设椭圆的标准方程为22221(0)x y a b a b+=>>,∴26a =,3a =,13c e a ==,1c =;2228b a c =-=,22198x y +=(4分) (II )△2PF Q 的周长是定值方法1:设()1122,,(,)P x y Q x y ,则2211198x y +=, ()()22222112111118(1)(3)93x xPF x y x =-+=-+-=-,∵103x <<,∴1233x PF =-,(7分) 在圆中,M 是切点,∴222222111111||||88(1)893x PM OP OM x y x x =-=+-=+--=,(11分)∴211113333PF PM x x +=-+=, 同理23QF QM +=,(13分)∴22336F P F Q PQ ++=+=, 因此△2PF Q 的周长是定值6.…………(14分)方法2:设PQ 的方程为(0,0)y kx m k m =+<>,由⎪⎩⎪⎨⎧=++=18922x x m kx y ,得072918)98(222=-+++m kmx x k (5分)设),(),,(2211y x Q y x P ,则2219818k kmx x +-=+,222198729k m x x +-=,∴||1||212x x k PQ -+=2122124)(1x x x x k --+===(8分) ∵PQ 与圆822=+y x=,即2122k m +=,∴26||89kmPQ k=-+,(9分) ∵2PF ===∵103x <<,∴1233x PF =-,(12分) 同理2221(9)333x QF x =-=-,(13分)∴12222226666663898989x x km km kmF P F Q PQ k k k +++=--=+-=+++,因此△2PF Q 的周长是定值6.…………(14分)20、(13分)设有穷数列{a m }(m =1,2,3,4,…,n ;n =2,3,4,…,)满足以下两个条件:①10n i i a ==∑;②11ni i a ==∑;称{a m }为n 阶“单位数列”。