(完整版)同方向同频率简谐振动合成的公式及推导

o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
（2）相位差 (2k 1) π(k 0，1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
（1）相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0，1， ) 加强
（2）相位差
2
1
(2k 1) π
(k 0，1， )
A A A
1
2
减弱
（3）一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气（室温为 20C）中来 回摆动. 摆线长l 1.0 m，摆锤是半径r 5.0103 m 的铅球.求（1）摆动周期；（2）振幅减小 10％所需的时间；（3）能量减小10％所需 的时间；（4）从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.

A A1 A2
x
x1 A1 cos t x2 A2 cos(ωt π ) x x ( A2 A1 ) cos(ωt π)
o 2
A 2
A1
o
T
t
A
1) 相位相同 φ2 φ1 或 Δφ φ2 φ1 0
A A1 A2
相互加强
x A cos( t 1 ) A cos( t 2 ) 2) 相位相反 Δφ φ2 φ1 π
此结论对讨论各种波的干射、衍射极为有用。
二、 两个同方向不同频率简谐振动的合成 x1 A1 cos 1t A1 cos 2 π 1t
x2 A2 cos 2t A2 cos 2 π 2t
讨论 A1 A2 ,
x x1 x2
2 1 1 2 的情况
x y 2 1 2 A1 A2
π y A2 cos( t ) 2 0 质点沿顺时针方向运动
2 2
y
A1
A2
o
x
A2 y

x A1 cos t
o
A1
x
2 质点沿逆时针方向运动
用 旋 转 矢 量 描 绘 振 动 合 成 图
两 相 互 简 垂 振 直 动 同 的 频 合 率、 成 不 图 同 相 位
1 1 可见 π ( 2 1 )T拍 ∴ T拍 2 1 拍
拍 2 1
拍频（振幅变化的频率）
注意:书上的拍频写成，此处的拍频写成拍
2 1 1 2
( 1 2 ) / 2 1 2 , 1 2
(C)
3k / m /( 2π )

2 1 2 2
x
x
o ϕ2
ω A2
A1
A = A1 − A2 ϕ = ϕ2
o
T
t
A
相位差
ϕ 2 − ϕ1 = 2 k π
A = A1 + A2
ϕ 2 − ϕ1 = (2k + 1)π
A = A1 − A2
当A1=A2 时，A=0
(k = 0 ， 1， ) ± L
相互加强
相位差
(k = 0 ， 1， ) ± L
A1
在任一时刻离开坐标原点位移为： 在任一时刻离开坐标原点位移为： (2) ϕ 2 − ϕ1 = π 两个分运动反相位， 两个分运动反相位， 得
A2 y= x A1
y A2
o
A1
x
(3) φ2−φ1=π/2，得
x y + 2=1 2 A1 A2
2
2
这是坐标轴为主轴的椭圆，质 这是坐标轴为主轴的椭圆， 点的轨迹是顺时针旋转。 点的轨迹是顺时针旋转。 (4) φ2−φ1=3π/2，仍然得
三、相互垂直的简谐振动的合成 1. 频率相同
若质点同时参与两个同频率的相互垂直的分运 动，其位移表达式分别为
x = A1 cos(ωt + ϕ1 ) y = A2 cos(ωt + ϕ 2 )
消去时间参数， 消去时间参数，得
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2
x = A1 cos(ω1t + ϕ1 ) y = A2 cos(ω 2t + ϕ 2 )
李 萨 如 图
ϕ1 = 0
π π 3π π ϕ 2 = 0, , , , 8 4 8 2

x
- (A1sinφ1 + A2sinφ2)sinωt
x
令Acosφ = A1cosφ1 + A2cosφ2，Asinφ = A1sinφ1 + A2sinφ2, 则x = Acosφcosωt – Asinφsinωt =Acos(ωt + φ),
其中
A
A12

A22

2 A1 A2
cos(2
(2)有n个同一直线同频率的简谐振动，它们的振幅都
是ΔA，相差都是Δφ，第一个振动的初相为零。求N个C
简谐振动的振幅和初相。
nΔφ
M Δφ ΔA5
振幅 A A sin(n / 2)
r Δφ A ΔA 4Δφ
sin( / 2)
初相为 1 (π ) 1 (π n) n 1
利用和差化积公式可得合振动为
同频率的简谐振动合
x

x1

x2

2 A cos(2
1
2
t) cos(2
1
2
t
成之后不是简谐振动， )也没有明显的周期性。
当两个分振动的频率比较大而差异比较小时：|ω2 - ω1| << ω2 + ω1，方程就表示了振幅按2Acos[(ω2 - ω1)t/2]变化 的角频率为(ω2 + ω1)/2的“近似”的简谐振动。
矢量的合成如图所示。
终点都在以C为圆心的圆周上。
设圆的半径为r，每个矢量对 A 2r sin
应的圆心角都是Δφ ，因此
2
这是多个 等幅同频
全部矢量对应的圆 心角是nΔφ，因此
A 2r sin n
2

合振动的振幅随时间作缓慢的周期性的变化， 合振动的振幅随时间作缓慢的周期性的变化，振 动出现时强时弱的拍现象 拍现象。 动出现时强时弱的拍现象。 拍频:单位时间内强弱变化的次数。 拍频:单位时间内强弱变化的次数。 ω2 − ω1 γ= = γ 2 − γ1 2π
同方向不同频率的两个简谐振动的合成 拍
同方向同频率的两个简谐振动的合成
C
r A
O
r a1
r r a3 α a2
α
r a4 α
rα a5
M
X
因各个振动的振幅相同且相差依次恒为 α ，上图 为圆心的圆周上， 中各个矢量的起点和终点都在以 C为圆心的圆周上， 为圆心的圆周上 根据简单的几何关系， 根据简单的几何关系，可得
∠OCM = Nα
同方向同频率的两个简谐振动的合成
x1
t
x2
t
x
t
同方向不同频率的两个简谐振动的合成 拍
反相迭加，合振幅最小。 反相迭加，合振幅最小 当A1=A2 时，A=0。 。 (3)通常情况下，合振幅介于 通常情况下， 通常情况下 和 之间。 之间。
同方向同频率的两个简谐振动的合成
个同方向、同频率的简谐振动，它们的振幅相等， 例15-4 N个同方向、同频率的简谐振动，它们的振幅相等， 15初相分别为0, , 2a, 依次差一个恒量a， 初相分别为0, a, 2 , ..., 依次差一个恒量 ，振动表达式可 写成
求它们的合振动的振幅和初相。 求它们的合振动的振幅和初相。
采用旋转矢量法可使问题得到简化， 解:采用旋转矢量法可使问题得到简化，从而避开 烦琐的三角函数运算。 烦琐的三角函数运算。 根据矢量合成法则， 个简谐振动对应的旋转矢 根据矢量合成法则，N个简谐振动对应的旋转矢 量的合成如下图所示： 量的合成如下图所示：

x1 (t ) = a cosωt x2 (t ) = a cos(ωt + δ ) x3 (t ) = a cos(ωt + 2δ )
C
Nδ
R
A
aN
⋮ x N ( t ) = a cos[ ω t + ( N − 1)δ ]
O
δ
a3
a1 P
在∆COM中：A = 2 R sin( N δ / 2 ) 中 上两式相除得： 上两式相除得： 在∆OCP中： a = 2R sin(δ / 2) 中
2
A2 y= x 为直线方程 A1
利用旋转矢量合成
∆ϕ = 0
2 1
y
8 7 6
4 4
y
1 2
3
3 7 6
4Байду номын сангаас
8
x
5
5 3
2 1
播 放 动 画
16
5 6 7
x
8
2. |ϕ 2
− ϕ1 | π =
2 2
反相位
y
x y 2xy =0 + + A1 A2 A1 A2
3
利用旋转矢量法求合振动也可得到相同的结果。 •利用旋转矢量法求合振动也可得到相同的结果。 取质点振动的平衡位置O为 取质点振动的平衡位置 为 坐标原点，振动方向沿OX轴。A 坐标原点，振动方向沿 轴 2 点作两个长度分别为A 从O点作两个长度分别为 1、 点作两个长度分别为 ϕ2 ϕ A2的矢量 A1 , A2 ，它们在 它们在t=0时 时 与X轴的夹角分别为ϕ1、ϕ2。 轴的夹角分别为ϕ 轴的夹角分别为
x1 = 4 cos 3t ,
= A cos(3t + ϕ )

从数学上讲 任何形式的周期函数都可通过付里叶级数分解 成一系列不同频率、不同振幅的谐振动之和； 成一系列不同频率、不同振幅的谐振动之和；而非 周期振动可通过傅里叶积分把它展成无数个频率连 续分布的谐振动。 续分布的谐振动。 将任一周期性振动 x(t +T) = x(t) 按付立叶级数展开 a0 ∞ x (t ) = + ∑ (an cos nω t + bn sin nω t ) 2 n=1 2 π 若周期振动的频率为： 若周期振动的频率为：ν ω =2 = πν T 则各分振动的频率为:ν、2ν、3ν、… 则各分振动的频率为: （基频 , 二次谐频 , 三次谐频 , …） ） 由于所包含的频率取分立值，这类频谱称为离散谱。 由于所包含的频率取分立值，这类频谱称为离散谱。
二. 同方向不同频率简谐振动的合成 分振动 合振动
x2 = Acos(ω2t +ϕ2)
x = x + x2 1
1 1 x = 2 A cos [(ω 2 − ω1 )t + (ϕ 2 − ϕ1 )] ⋅ cos [(ω 2 + ω1 )t + (ϕ 2 + ϕ1 )] 2 2
x = Acos(ω t +ϕ1) 1 1
图(a) 中实线所代表的周期性振动可分解为基频 倍频的两个简谐振动的叠加。 和3倍频的两个简谐振动的叠加。 倍频的两个简谐振动的叠加 而图(b)则是一种“方波”振动信号， 而图 则是一种“方波”振动信号，它所包含 则是一种 的简谐振动成分就多了。 的简谐振动成分就多了。 这里用竖直线段在横坐标上的位置代表所包含 简谐振动的频率，竖直线高度代表所对应振幅， 简谐振动的频率，竖直线高度代表所对应振幅，该 称为振动频谱 图(c)称为振动频谱。 称为振动频谱。

2）相位差 2 1 (2k 1)π
(k 0 ， 1, )
A A1 A2
合成的振幅最小
合成的振动的初相和振幅大的分振动的初相相同
4 –2 两个同方向同频 1)π (k 0 ， 1, )
x1 A1 cost x2 A2 cos(t π ) x ( A2 A1 ) cos(t π)
2 A2 cos 2 A12 cos 2 1 A2 cos 2 2 2 A1 A2 cos 1 cos 2 2 A2 sin 2 A12 sin 2 1 A2 sin 2 2 2 A1 A2 sin 1 sin 2
2 A2 A12 A2 2 A1 A2 cos 1 cos 2 sin 1 sin 2
A2
2
0

A
x2
x A cos(t )
x x1 x2
x2
1

x1
A1
x
x
A1 sin 1 A2 sin 2 tan A1 cos 1 A2 cos 2 2 2 A A1 A2 2 A1 A2 cos( 2 1 )
4 –2 两个同方向同频率振动的合成 根据余弦定理
3）一般情况
A A1 A2
相互削弱
A1 A2 A A1 A2
4 –2 两个同方向同频率振动的合成
本节练习 1 （D） 2. 两个分振动的圆频率相同，所以，合振动 旋转矢量的大小为常量，合振动的圆频率 也和分振动的圆频率相同。
4 –2 两个同方向同频率振动的合成
作业
习题 4-4
x
x
2
o 2
A 2

t
一个拍
合振幅变化的频率即拍频
拍
|
2 1 2
|| 2
1
|
拍现象是一种很重要的物理现象。
手风琴的中音簧： 键 盘 式 手 风 琴 （ Accordion) 的 两 排 中 音 簧 的 频 率大概相差6到8个赫兹，其作用就是产生“拍” 频。而俄罗斯的“巴扬”---纽扣式手风琴则是单 簧片的，因此没有拍频造成的颤音效果。
如果 A1 A2 则 A=0
合成振动
T 2
T
3T 2
2T
t
x2
x1
T 合成振动 3T
2
2
T
2T t
一般情况 为其他任意值，则：
A1 A2 A ( A1 A2 )
x
合成振动
T
3T
2
2
o
T
2
t
T
上述结果说明两个振动的相位差对合振动起着 重要作用。
例: 两个沿同一直线且具有相同振幅和周期的谐振动
两个同方向频率相近的简谐振动的合成 为合振幅随时间作缓慢变化的准简谐振动（拍）
合振幅变化的频率即拍频 拍 | 2 1 |
两个振动方向垂直频率相同的简谐振动的合成可能仍 为直线振动（而且是谐振动）也可能是圆运动，和椭 圆运动。
课后实验：
1. 请你测量一根吉他琴弦的振动频率。
2. 敲击盛水的玻璃酒杯能产生清晰的音调.试用 音叉把这些音调校准到你所需要的频率看看是否 能把他们排列起来构成一个八度音阶。
4
2
9
4
与合成相反：一个圆运动或椭圆运动可分解为
相互垂直的两个简谐振动。
四、两个互相垂直不同频率简谐振动的合成
如果两个相互垂直的振动的频率不相同，它们 的合运动比较复杂，而且轨迹是不稳定的。下面只 讨论简单的情形。

(A1 sin1 A2 sin2 )sint
合振幅
令： A1 cos1 A2 cos2 Acos 代入上式：
A1 sin1 A2 sin2 Asin
2
x ( A1 cos1 A2 cos2)cost (A1 sin1 A2 sin2 )sint
Acos cost Asin sint Acos(t ) x Acos(t )
x1(t) a cost
M aN
x2 (t) a cos(t ) x3(t) a cos(t 2 )
C
R N
A
a3
xN (t) a cos[t (N 1) ]O a1 P
在COM中：A 2R sin(N / 2)
上两式相除得：
在OCP中： a 2Rsin( / 2)
7
A a sin(N / 2) sin / 2
若 A1 A2, A 2A1
2.当 2 1 （2k 1） (k 0,1,2, ) 时,
A
A12
A
2 2
2 A1
A2
cos(
2
1
)
| A1 A2 | 合振动振幅最小。
若 A1 A2, A 0
A2
3.一般情况 | A1 A2 | A | A1 A2 |
5
A A2 A1
A2 A A1 A A1
第二节
简谐振动的合成
1
一、同方向同频率简谐振动的合成
在同一直线上同频率的两个简谐振
动分别为：
x1 A1 cos(t 1),
x2 A2 cos( t 2 )
• 代数方法： 振动合成
x x1 x2 A1 cos(t 1) A2 cos(t 2 )
(A1 cos1 A2 cos2) cost

同方向的简谐振动的合成
§10-5 同方向的简谐振动的合成
1.同方向同频率的两个简谐振动的合成
设一质点同时参与沿同一方向的两个独立的 同频率的简谐振动，两个简谐振动的频率为 ω，
振动方向为 X 轴方向，以 x1和 x2 分别代表同一
个质点的两个运动位移：
x1 A1 cos(t 10) x2 A2 cos(t 20)
解：已知 A = 20 cm
A1 = 17.3 cm A2 =[A2 +A12 -2AA1cos( - １)]1/2
= 10 cm
o
A
A2
１ A1 x
∵A2 = A12 + A22 + 2A1A2 cos ( 1 - 2 ) ∴ cos (1 - 2 ) = [A2 - A12 - A22] / 2A1A2
同相迭加，合振幅最大。
(2)当D 2010(2k+1) (k=0及 正负整数), cos(20-10)=0, 有
O
A1
A A1 A2 A A1 A2
A2
O
X
反相迭加，合振幅最小。 当A1=A2 时，A=0。
(3)通常情况下，合振幅介于 和
之间。
A1 A2 A1 A2
补例1两个同方向同频率的简谐振动，其合 振动的振幅为 20 cm，与第一个简谐振动的 相位差为 - １= π/6，若第一个简谐动的振 幅为 17.3 cm，试求： 1、第二个简谐振动的振幅 A2 2、第一、二两个简谐振动的相位差 1 - 2
旋转矢量图示法
矢量沿X 轴之投影表征了合运动的规律。
A1
10
X
O
x2
x x1
A
同方向同频率的两个简谐振动的合成

ϕ
A2
x
O C A1
N −1 ∆ϕ ϕ = 合振动表达式 2 x ( t ) = A cos( ω t + ϕ ) sin(N∆ϕ / 2) N −1 = A0 cos(ω t + ∆ϕ ) sin(∆ϕ / 2) 2
讨论1： 讨论 ： 当 δ
= ±2kπ k = 0,1,2,L sin(N∆ϕ / 2) A = lim A0 = NA0 sin(∆ϕ / 2)
四、两个相互垂直的同频率简谐振动的合成
某质点同时参与两个同频率的互相垂直方向的简谐运动
x = A1 cos(ω t + ϕ 1 ) y = A2 cos(ω t + ϕ 2 )
合振动的轨迹方程为
x y 2 xy 2 cos(ϕ 2 − ϕ 1 ) = sin (ϕ 2 − ϕ 1 ) + 2− 2 A1 A2 A1 A2
'
各分振动矢量依次相接， 各分振动矢量依次相接，构 成闭合的正多边形， 成闭合的正多边形，合振动 的振幅为零。 的振幅为零。
三、同方向不同频率的简谐振动的合成
某质点同时参与两个不同频率且在同一条直线上的简谐振动
x1 = A1 cos(ω 1 t + ϕ 1 )
x 2 = A2 cos(ω 2 t + ϕ 2 )
A2 y=− x A1
y
x2 y2 2 xy + 2+ =0 2 A1 A2 A1 A2
x
合振动的轨迹是一条通过原点的直线
讨论3 讨论
∆ϕ = ϕ 2 − ϕ 1 = π / 2 x2 y2 合振动的轨迹是的椭圆 合振动的轨迹是的椭圆 + 2 =1 2 A1 A2 方程， 方程，且顺时针旋转

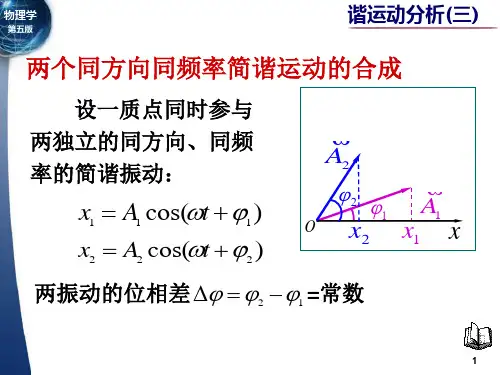
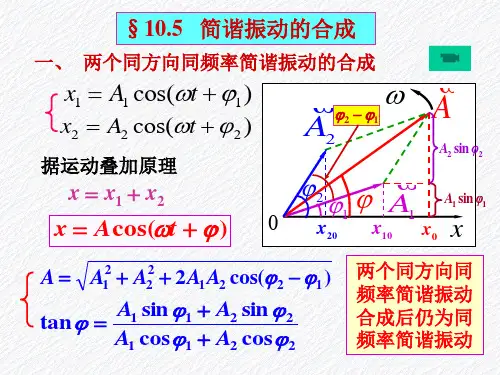
同方向同频率简谐振动的合成初相位的推导好吧，今天咱们聊聊一个有趣的话题，关于同方向同频率的简谐振动合成初相位的推导。

这听起来可能有点复杂，但其实就像咱们生活中的很多事情一样，抓住核心，就能简单明了。

想象一下，两个小朋友在操场上同时摇摆秋千，他们都在同一个频率上，像极了两个精灵在空中翩翩起舞。

你知道的，当他们都朝同一个方向摇摆的时候，他们的动作就会变得非常和谐。

就像是无形的音乐在操场上流淌，彼此之间心有灵犀。

这就是咱们所说的同方向同频率简谐振动。

就好比两根弦一起拨动，发出的声音和谐动听。

想想看，如果这两个小朋友的秋千一前一后地摆动，那可就热闹了，像是东边一声雷，西边一阵风，谁也跟不上谁的节奏。

这种情况就叫做相位差。

相位差就像是朋友之间的默契，有时候对得上了，有时候却像是两条平行线，永远也不会相交。

咱们如果要找出这两个振动的合成初相位，首先得先了解振动的特点。

简谐振动的公式就像是一个老朋友，随时可以叫出来，它的样子是这样的：x(t) = A cos(ωt + φ)。

这里的A就是振幅，ω是角频率，而φ就是初相位。

简单来说，振幅决定了秋千摆动的幅度，频率则是秋千摆动的速度，初相位就像是我们起跑的起点。

当这两个振动在同一频率下摇摆时，它们的合成可以用简单的数学工具来实现。

首先把两个振动的表达式写出来，记得要把相位带上。

假设第一个振动是A₁ cos(ωt +φ₁)，第二个振动是A₂ cos(ωt + φ₂)。

这时候就像是厨房里调配酱料，A₁和A₂就分别是两种调味料，而φ₁和φ₂则是不同的味道。

要想合成出一锅好汤，就得把这两种调味料巧妙地搅拌在一起。

我们可以利用三角函数的合成公式，巧妙地把这两条振动结合在一起。

结合起来后，你会发现振动的合成幅度A和合成初相位φ就跃然纸上。

就像是调皮的小孩，俩人在一起玩耍，总是能碰撞出不一样的火花。

这合成幅度A可以用根号(A₁² + A₂² +2A₁A₂ cos(φ₁ φ₂))来计算，而合成初相位φ则是用tan(φ) = (A₁ sin(φ₁) + A₂sin(φ₂)) / (A₁ cos(φ₁) + A₂ cos(φ₂))。

三角函数法对同方向同频率简谐振动合成的求解
同方向同频率简谐振动是指两个物体以相同的角频率且方向一致地做简谐振动。

这种振动常常出现在机械振动、波动和电磁振动等领域中。

因此，对同方向同频率简谐振动的合成求解是很重要的。

三角函数法是求解简谐振动合成问题的常用方法，它利用三角函数的性质，将振动方程表示为三角函数的形式，从而方便进行进一步的计算。

下面我们将介绍三角函数法对同方向同频率简谐振动合成的求解步骤。

（1）假设两个物体分别做简谐振动，振幅为A1和A2，初始相位分别为φ1和φ2，角频率均为ω。

（2）写出两个物体的振动方程：
x1 = A1sin(ωt + φ1)
（4）根据三角函数的和差公式，将上式化简为：
x = [A1cos(φ1) + A2cos(φ2)]sin(ωt) + [A1sin(φ1) + A2sin(φ2)]cos(ωt)（6）求出两个简谐振动的振幅和相位，即可求出合成振动的振幅和相位。

振幅：
相位：
（7）利用上式求出合成振动的振幅和相位后，可以得到合成振动的振动方程：
其中，A为合成振动的振幅，φ为合成振动的相位，ω为角频率，t为时间。

ω1 − ω2 << ω1 ≈ ω2
dengyonghe1@
设
A1 = A2 = A，
ω1 ≈ ω 2
x1 = A cos(ω1t + ϕ ) x 2 = A cos(ω 2t + ϕ )
合成后 x = x1 + x 2
= A cos(ω1t + ϕ ) + A cos(ω 2t + ϕ )
x
dengyonghe1@
o
2.注意几点 2.注意几点 (1). 当
Hale Waihona Puke ∆ϕ = ϕ 2 − ϕ1 = 2kπ ( k = 0,±1,±2,L) 时,
两个同相
A=
A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 ) x = A1 + A2
2 1 2 2
合振动振幅最大。 合振动振幅最大。 若
一、同方向同频率的两个简谐振动合成
质点同时参与两个振动， 质点同时参与两个振动，只 研究两个同方向同频率的振动合 成。 分振动
x1 = A1 cos(ωt + ϕ1 ) x 2 = A2 cos(ωt + ϕ 2 )
振动合成
x = x1 + x 2
dengyonghe1@
1.利用矢量法求合振动 利用矢量法求合振动
dengyonghe1@
解：直接代公式： 直接代公式：
A = (90 2 ) + (200 2 ) = 220 2
2 2
200 2 ϕ = tan ( ) = 65.80 90 2
−1
∴ u = 220 2 cos(100πt + 65.8 )

A
ω 1
A = A − A2 1
合振动 x 不再是简谐振动
O
A1
x
x = x1 + x2
振幅相同不同频率的简谐振动的合成 1. 分振动
x1 = Acosω1t
x2 = Acosω2t
2. 合振动
x = x1 + x2 = Acosω1t + Acosω2t
= 2Acos(
振幅
ω2 −ω1
2
)t ⋅ cos(
t
ω0 3ω0 5ω0
锯齿波频谱图
ω
O
方 波
基频为v （基频为 0）
方 O 波 的 分 解 O 图
O
v0
3v0 5v0
x1+ x3+ x5
O
§11.3 阻尼振动和受迫运动
一. 阻尼振动
1. 受力特点 线性恢复力 阻尼力 F f
F = −kx
f = −µ x ɺ
µ k x ɺ + x+ x =0 ɺ ɺ m m
• 振幅衰减随时间按指数衰减
2 • 角频率 ω0 − n2
(2) 过阻尼和临界阻尼
临界阻尼: 临界阻尼 过 阻 尼:
2 n2 = ω0 2 n2 > ω0
在临界阻尼状态下，物体回到并 临界阻尼状态下， 停留在平衡位置， 停留在平衡位置，所需时间最短
受迫振动（ 二. 受迫振动（在外来策动力作用下的振动）
受迫振动 x 驱动力 相位差
同年7月大桥因一场大风 引起桥的共振而倒塌
1940年建成的塔科曼大桥
1.受力特点 受力特点
弹性力 阻尼力 周期性策动力
− kx
ɺ − µx
F = F0 cosωt

§4.4 简谐振动的合成
一.同频率、同一直线上的简谐振动的合成 分振动：x1 =A1cos( t+1 ) x2 =A2cos( t+2 )
合振动： x= x1+x2 = Acos( t+ )
A A1 A2 2 A1 A2cos( 2 1 )
2
2
A1sin1 A2sin 2 tg A1cos1 A2cos 2
x y 2 1 2 A1 A2
y
2
2
合振动不再是谐振动。
y
x
x 左旋
右旋
2 -1=/2
2 -1=-/2
21
两个频率相同、 振幅不同的互
相垂直简谐
Δ=0 Δ=/4 Δ=/2 Δ=3/4
振动的合成
Δ=
Δ=5/4
Δ=3/2
Δ=7/4
22
四.不同频率垂直谐振动的合成 李萨如图形 x =A1cos(1 t+1 ) y =A2cos(2 t+2 )
2， = 0 （临介阻尼）
x e t C1 C 2 t
3， < 0 （欠阻尼）
xe
e
t
t
C cos
1
C e
1
i 0 2 2 t
C2 e
2
i 0 2 2 t

2 2
0 t C2 sin 0 t
2
2 2

( 2 1 )

2
o
x
10
例题4.17 求同方向、同频率、同振幅、依次间相 位差均为的N个谐振动的合振动方程。 光的衍射 解
选择适当的计时起点，使某个简谐振动的初 相为零，则有