二、同方向不同频率两个简谐振动的合成剖析
- 格式:ppt
- 大小:1.99 MB
- 文档页数:19


二、振动的合成实际生活中,一个系统往往会同时参与两个或更多的振动。
例如悬挂在颠簸船舱中的钟摆,两列声波同时传入人耳等。
一般的振动合成显然是比较复杂,下面仅讨论几种间单情况的简谐振动合成。
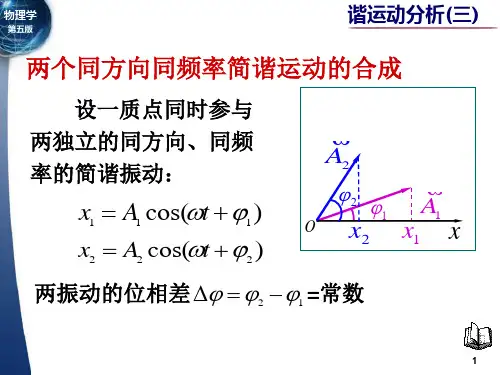
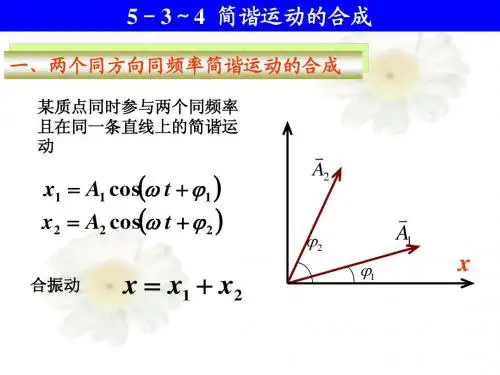
一、同方向同频率简谐振动的合成若两个同方向的简谐振动,频率都是,它们的运动方程分别为因振动是同方向的,所以这两个谐振动在任意时刻的和位移应在同一直线上,且等于这两个振动位移的代数和,即合位移仍为简谐振动二、两个同方向不同频率简谐振动的合成拍如果两个简谐振动的振动方向相同而频率不同,那么合成后的振动仍与原振动方向相同但不再是简谐振动。
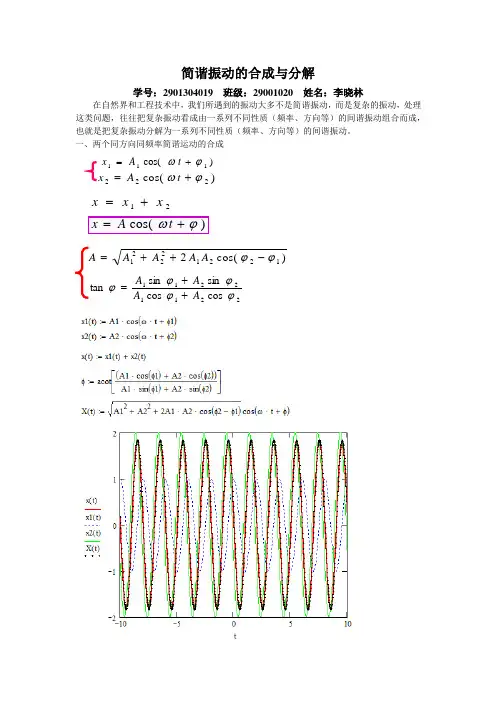
现设两简谐振动的振幅都为A,初相位为零,它们的振动方程分别为合成振动方程为若两个分振动的频率都较大且其差很小时,即,合振动可看作为振幅随时间缓慢变化的近似谐振动,振幅随时间变化且具有周期性,表现出振动或强或弱的现象,称拍,变化的频率称拍频,变化的振幅为变化的频率为三、相互垂直的简谐振动的合成李萨如图如果两个简谐振动分别在x轴和y轴上进行,他们的振动方程分别为合成后,可得质点的轨迹为椭圆方程若两分振动有不同的频率,且两频率之比为有理数时,则合成后的质点运动具有稳定、封闭的轨迹。
称其为李萨如图形。
程序编写我们已经在第一讲中体验了matlab的编程,可是你一定会生出这样的问号,辛辛苦苦在命令窗口写的一大堆代码怎么不保留?不用担心,matlab程序和其他编程工具一样,也有专门的文件格式,称m文件,文件名形式为“文件名.m”。
你可以用matlab自带的编辑器来输入你的程序代码,当然你也可以用其它编辑器或最经济的文本编辑器,不过别忘记添加文件名的后缀“.m”。
下面,请跟我一起用m文件编辑器来编写matlab程序。
例题:两个振动方向相同而频率不同的简谐振动方程分别为合成后的方程是请用matlab程序描述合成波和拍频现象。
编程:第一步:点击matlab图标,打开程序窗口。
第二步:选file—new—m-file,打开编辑器。






同方向不同频率的简谐振动的合成好,今天咱们就来聊聊同方向不同频率的简谐振动合成。
别急,听我慢慢说,保证你一听就明白。
你得知道,简谐振动就像是一个物体在做上下左右那种规律性的摆动,感觉就像小孩子在秋千上摇来荡去那样,一来一回,一直不带停的。
你看过钟摆摆动吧?就那种感觉,越来越平稳,越过越规律,跟着一个固定的节奏跑。
但是,今天我们不光是讲单一的那种振动,我们要聊的可是两种频率不同的振动合成,它们在一起会怎么样呢?想象一下,两个人在同一个舞池跳舞,他们的舞步却不完全一致。
一个跳得慢,一个跳得快,开始的时候,大家还好像能勉强跟上,但过了一会儿,慢的那个开始觉得有点跟不上节奏,快的那个又有点等不及了。
是不是有点儿这种意思?没错,这就像两种不同频率的简谐振动,如果它们方向相同,但频率不同,合成出来的效果就有点复杂了。
你可以这样想:其中一个振动快得像飞一样,另一种则慢得像老牛拉破车,结果它们俩在同一个方向上“跑”来跑去。
它们的振动轨迹会不断交错,甚至会出现“合成振动”的现象,你可以理解成两者互相“纠缠”的结果。
要是它们的频率差别特别大,你会看到,快的那个有时候走得远了,慢的还在原地打转,合成的波形看上去就有点像一张波浪形的图,忽高忽低,像是过山车一样的刺激。
但是,有趣的地方就在这了!你看,两个不同频率的振动合成之后,它们的频率不单单是快的和慢的,而是产生了一种新的频率,这个频率叫做“合成频率”。
它就像是你听到两首歌,分别有各自的节奏,但一旦合并在一起,突然间你听到了一个新的旋律,乍一听挺陌生,但又有点儿奇妙的和谐感。
这个合成频率一般是由两种原始振动的频率差所影响的,也就是说,快的那个和慢的那个在一起后,调皮地产生了一种“中间”频率,所有的节奏似乎变得更有韵律了。
再说到合成的幅度,那更是有趣!幅度就像是你跳舞时的力度和气势。
你跳得越用力,别人就能感受到你那个震撼。
而在这两种不同频率的振动合成中,幅度也不是那么简单的加和,而是依赖于它们之间的相对位置。