下载文档原格式
第4章 习题与答案4-1作简谐振动的物体，每次通过同一位置时，不一定相同的量是 [ ] (A) 位移 ； (B) 速度 ； (C) 加速度； (D) 能量。
[答案：B ]4-2 把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为 [ ](A) π； (B) π/2； (C) 0； (D) θ [答案：C ]4-3 谐振动的振动曲线如题4-3图所示，则有[ ] （A ）A 超前π/2； （B ）A 落后π/2； （C ）A 超前π； （D ）A 落后π。
[答案：A ]4-4 一个质点作简谐振动，振辐为A ，在起始时刻质点的位移为A /2，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为题4-4图 中哪一个? [ ][答案：B ]4-5 两个质点各自作简谐振动，它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点恰在最大负位移处。
则第二个质点的振动方程为 [ ] (A) )π21cos(2++=αωt A x ； (B) )π21cos(2-+=αωt A x ； (C) )π23cos(2-+=αωt A x ； (D) )cos(2π++=αωt A x 。
[答案：A ]4-6 已知某简谐振动的振动曲线如题4-6图所示。
则此简谐振动的振动方程（SI ）为 [ ](A) 题4-4图题4-3图（A ）220.02cos()33x t =π+π；（B ）220.02cos()33x t =π-π；（C ）420.02cos()33x t =π+π；（D ）420.02cos()33x t =π-π。
[答案：C ]4-7 弹簧振子作简谐振动，先后以相同的速度依次通过A 、B 两点，历时1秒，质点通过B 点后再经过1秒又第二次通过B 点，在这2秒内质点通过的总路程为12cm ，则质点的振动周期和振幅分别为 [ ]（A ）3s 、12cm ； （B ）4s 、6cm ； （C ）4s 、9cm ； （D ）2s 、8cm 。
电子技术与软件工程Electronic Technology & Software Engineering电子技术Electronic Technology 同方向同频率简谐振动合成问题求解方法的研究贾冬梅（中北大学信息商务学院山西省晋中市030600 ）摘要：本文分别运用解析法和旋转矢量法来求解两个同方向同频率简谐振动的合成问题并分析总结了它们冬自的特点.通过对比发 现：运用旋转矢量法比解析法更为直观有效，它可以生免去对物理公式的记忆和复杂的数学计算.但是在一般情形下，运用解析法求解更为有效.对于合振动初相位的确定，运用旋转矢量法比解析法更加直观、有效和便捷.关键词：振动合成；解析法；旋转矢量法；振幅；初相简谐振动是机械振动中最简单、最基本的振动形式，任何复杂 的振动都可以看作是简谐振动的合成旳。
而同方向同频率的简谐振 动的合成又是简谐振动的合成中最简单最重要的形式，它为波干涉 和衍射现象的分析奠定了理论基础，因此研究同方向同频率简谐振 动的合成有着十分重要的意义。
寻求一种高效便捷的求解简谐振动 合振动的振动的方法成为了解决同方向同频率简谐振动的合成的关 键3」。
对于同方向同频率简谐振动的合成问题，大学物理教材中 常使用旋转矢量法和解析法来进行讨论分析‘网。
下面分别运用解 析法和旋转矢量法来求解同方向同频率简谐振动合成问题，分析总 结它们各自的特点，为这类问题的分析和求解提供一些参考和借鉴。
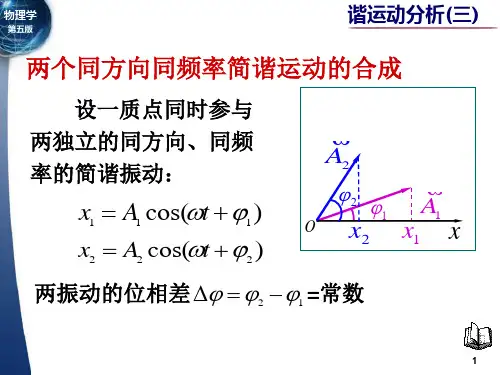
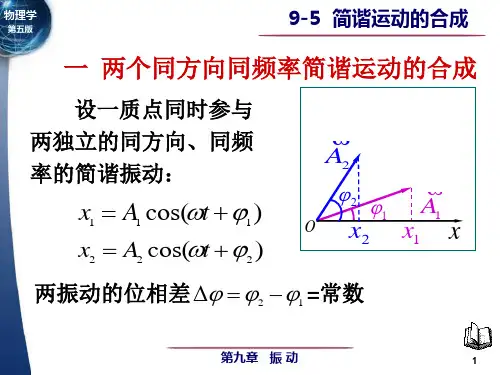
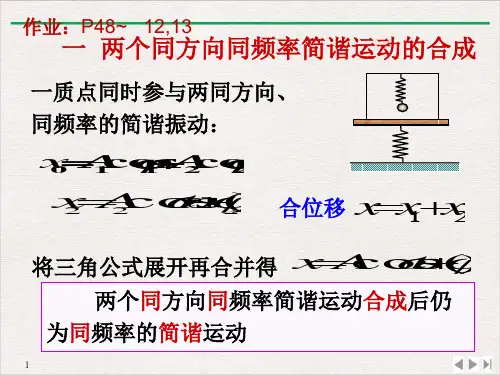
1两个同方向同频率简谐振动的合成设两个简谐振动都沿着x 轴方向振动，平衡位置都为坐标原点， 它们振动的角频率3,振幅分别为A]和A2，初相分别为®和％， 它们的振动方程分别为：x,=A| cos （（ot+（p]） x 2=A 2 cos （（ot+（p 2）求这两个解析振动的合振动。
1. 1解析法由于两个简谐振动都沿着X 轴方向振动，所以这两个简谐振动在任一时刻合振动的位移也应在X 轴方向上，且合振动的位移X 等 于这两个分振动位移的代数和，即：X=X]+x 2将分振动的方程X1和X2代入上式展开整理：x = x }+x 2= A } COS （＜zX + % ） + 厦2 COS （m + 02 ）=4 cos （p 、cos - /1] sin （p } cos cotA 2 cos （p 2 cos cot- A 2s\n （p 2 sin cut=（A, cos （p 、+ A 2 cos %） cos cot sin （p 、4- A 2 sin （p 2） sin cot 令 A cos （p=A] cos （p]+A 2 cos （p 2 A sin （p=A 1 sin （P]+A 2 sin （p 2 得至lj x=A cos （p coscot-A sin （p sin （ot=A cos （（ot+（p ）这一结果表明：两个同方向同频率简谐振动的合振动依旧是一 个简谐振动，且合振动的频率与分振动的频率相同都等于3,合振 动的振幅和初相可以表示为：A = J （/sin 0）2 +（/cos （p ）2=J A ： + / j + 2A t A 2 cos （02 - ％）川 sin 0 _ A x sin ® + A 2 sin （p 2t a n （p =------—-------------------A cos （p A x cos （p 、+ A 2 cos （p 21.2旋转矢量法如图1所示，4和力2分别为两个分振动的旋转矢量，它们以相 同的角速度绕o 点做逆时针转动，t=Os 时它们与x 轴正向的夹角分 别为卩和①。
大学物理学——振动和波振 动班级 学号 姓名 成绩内容提要1、简谐振动的三个判据（1）；（2）；（3）2、描述简谐振动的特征量： A 、T 、γ；T1=γ，πγπω22==T3、简谐振动的描述：（1）公式法 ；（2）图像法；（3）旋转矢量法4、简谐振动的速度和加速度：)2cos()sin(v00πϕωϕωω++=+-==t v t A dt dx m ； a=）（）（πϕωϕωω±+=+=0m 0222t a t cos -dtxd A 5、振动的相位随时间变化的关系：6、简谐振动实例弹簧振子：，单摆小角度振动：，复摆：0mgh dt d 22=+θθJ ,T=2mghJπ 7、简谐振动的能量：222m 21k 21A A Eω==系统的动能为：）（ϕωω+==t sin m 21mv 212222A E K ；系统的势能为：）ϕω+==t (cos k 21kx 21222A E P8、两个简谐振动的合成（1）两个同方向同频率的简谐振动的合成合振动方程为：）（ϕω+=t cos x A其中，其中；。
＊(2) 两个同方向不同频率简谐振动的合成拍：当频率较大而频率之差很小的两个同方向简谐运动合成时，其合振动的振幅表现为时而加强时而减弱的现象，拍频：12-γγγ=＊（3）两个相互垂直简谐振动的合成合振动方程：）（1221221222212-sin )(cos xy 2y x ϕϕϕϕ=--+A A A A ，为椭圆方程。
练习一一、 填空题1．一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1。
若将此弹簧截去一半的长度，下端挂一质量为m/2的物体，则系统的周期T 2等于 。
2．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为：A ＝ ；=ω ;=ϕ 。
3．如图，一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，做成一复摆。
已知细棒绕过其一端的轴的转动惯量J ＝3/2ml ，此摆作微小振动的周期为 。
1、 闭合曲面上各点电场强度都为零时，曲面内一定没有电荷（× ）2、 处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同，分子的平均平动动能也相同，则它们温度，压强都相同。
（√）3、 角速度的方向一定与外力矩的方向相同。
（ × ）4、 一物质系统从外界吸收一定热量，则系统的内能一定增加。
（×）5、 一质点作直线运动，速率为1232-=t ν（SI 制）则加速度大小=a t 6。
（ √ ）6、 质点系总动量的改变与内力无关。
（ √ ）7、 电势在某一区域内为常量，则电场强度在该区域内必定为零。
（√）8、 质点系总动能的改变与内力无关。
（ × ）9、 闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零。
（√）10、 将形状完全相同的铜环和木环静止放置在交变磁场中，并假设通过两环面的磁通量随时间的变化率相等，不计自感时则铜环中有感应电流，木环中无感应电流。
（√）11、 质点系总动量的改变与内力无关。
（ √ ）12、 质点系总动能的改变与内力无关。
（ × ）13、 作用力和反作用力对同一轴的力矩之和必为零。
（ √ ）14、质点速度大，加速度就一定大。
（×） 15、 在一个具体问题中，一个物体能否成为质点关键不在于物体的大小而在于物理问题与物体的大小形状是否有关。
（√）16、不同的参考系中，物体的运动情况都相同。
（×） 17、在直线运动中，质点的位移大小和路程相等。
（×） 18、 当物体的加速度大于0时，表示运动方向与参考方向相同，当加速度小于0时，表示运动方向与参考方向相反。
（×）19、质点速度大，加速度就一定大。
（×） 20、物体的运动可以看成是几个各自独立的运动的叠加。
（√） 21、两个动能相同的物体，质量大的动量小。
（×） 22、质点速度大，加速度就一定大。
（×） 23、 在一个具体问题中，一个物体能否成为质点关键不在于物体的大小而在于物理问题与物体的大小形状是否有关。
大学物理学——振动和波振 动班级 学号 姓名 成绩内容提要1、简谐振动的三个判据（1）；（2）；（3）2、描述简谐振动的特征量： A 、T 、γ；T1=γ，πγπω22==T3、简谐振动的描述：（1）公式法 ；（2）图像法；（3）旋转矢量法4、简谐振动的速度和加速度：)2cos()sin(v00πϕωϕωω++=+-==t v t A dt dx m ； a=）（）（πϕωϕωω±+=+=0m 0222t a t cos -dtxd A 5、振动的相位随时间变化的关系：6、简谐振动实例弹簧振子：，单摆小角度振动：，复摆：0mgh dt d 22=+θθJ ,T=2mghJπ 7、简谐振动的能量：222m 21k 21A A Eω==系统的动能为：）（ϕωω+==t sin m 21mv 212222A E K ；系统的势能为：）ϕω+==t (cos k 21kx 21222A E P8、两个简谐振动的合成（1）两个同方向同频率的简谐振动的合成合振动方程为：）（ϕω+=t cos x A 其中，其中；。
＊(2) 两个同方向不同频率简谐振动的合成拍：当频率较大而频率之差很小的两个同方向简谐运动合成时，其合振动的振幅表现为时而加强时而减弱的现象，拍频：12-γγγ=＊（3）两个相互垂直简谐振动的合成合振动方程：）（1221221222212-sin )(cos xy 2y x ϕϕϕϕ=--+A A A A ，为椭圆方程。
练习一一、 填空题1．一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1。
若将此弹簧截去一半的长度，下端挂一质量为m/2的物体，则系统的周期T 2等于 。
2．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为：A ＝ ；=ω ;=ϕ 。
3．如图，一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，做成一复摆。
已知细棒绕过其一端的轴的转动惯量J ＝3/2ml ，此摆作微小振动的周期为 。
