下载文档原格式
同方向同频率简谐振动的合成初相位同方向同频率的简谐振动听起来挺高深的，其实简单得很，就像咱们日常生活中常见的摇摇摆摆，咯吱咯吱的秋千。
你想象一下，两个小伙伴在秋千上并肩而坐，摇摆得十分起劲。
要是他们的节奏一致，频率相同，配合得就像小鸟在枝头上唱和，那真是美得不要不要的。
可要是他们的节奏不一样，那画面可就有点尴尬了。
就像一对恋人在跳舞，一人慢一人快，结果就是扭得稀巴烂。
什么是合成初相位呢？简单来说，就是这两个秋千的小伙伴最开始的起点。
如果他们同时开始摇，那就是同一个起点，一起飞，冲上云霄。
要是其中一个比另一个早一点，那他就提前起跑了。
这样一来，两个秋千的互动就会变得有趣多了。
我们可以想象一下，一个小伙伴先开始，结果另一个还在原地踏步，等他反应过来，已经被甩得老远，真是让人哭笑不得。
在物理学上，合成初相位能影响最终的合成振动。
想想两个秋千相遇的瞬间，波浪涌动的美妙感。
相位差越小，合成振动越强，感觉就像是合唱团里每个人的声音都在同一调上，和谐动人。
而相位差越大，合成振动就像是乐队里每个人都在演奏不同的旋律，结果可想而知，就是一场音乐会的灾难。
有趣的是，合成初相位也常常会出现在我们的日常生活中。
就像朋友聚会时，大家都来得差不多，气氛瞬间就热烈起来，大家一起聊，笑声不断，简直就是欢乐的海洋。
可要是有一个朋友迟到了，刚好打断了大家的欢乐，那气氛就会微妙地变了，像个捣蛋鬼一样。
你看，这个合成初相位的影响力，简直不容小觑。
想象一下你和好友一起打游戏，两个人的配合相当重要。
如果你们都在同一时间攻击敌人，那真是配合默契，像专业战队一样，敌人根本来不及反应。
而要是你总是慢半拍，那可就难了，往往被敌人痛揍一顿。
这时候就能真切感受到合成初相位的重要性，毕竟团队合作离不开每个人的步伐一致嘛。
合成初相位的概念还可以用在爱情中。
想想看，情侣之间的默契有多重要。
就像两个人的心灵感应，若是心有灵犀，瞬间就能理解对方的想法。
而若是两人总是各自为政，彼此心里没谱，那可是要闹出不少笑话的。
电子技术与软件工程Electronic Technology & Software Engineering电子技术Electronic Technology 同方向同频率简谐振动合成问题求解方法的研究贾冬梅（中北大学信息商务学院山西省晋中市030600 ）摘要：本文分别运用解析法和旋转矢量法来求解两个同方向同频率简谐振动的合成问题并分析总结了它们冬自的特点.通过对比发 现：运用旋转矢量法比解析法更为直观有效，它可以生免去对物理公式的记忆和复杂的数学计算.但是在一般情形下，运用解析法求解更为有效.对于合振动初相位的确定，运用旋转矢量法比解析法更加直观、有效和便捷.关键词：振动合成；解析法；旋转矢量法；振幅；初相简谐振动是机械振动中最简单、最基本的振动形式，任何复杂 的振动都可以看作是简谐振动的合成旳。
而同方向同频率的简谐振 动的合成又是简谐振动的合成中最简单最重要的形式，它为波干涉 和衍射现象的分析奠定了理论基础，因此研究同方向同频率简谐振 动的合成有着十分重要的意义。
寻求一种高效便捷的求解简谐振动 合振动的振动的方法成为了解决同方向同频率简谐振动的合成的关 键3」。
对于同方向同频率简谐振动的合成问题，大学物理教材中 常使用旋转矢量法和解析法来进行讨论分析‘网。
下面分别运用解 析法和旋转矢量法来求解同方向同频率简谐振动合成问题，分析总 结它们各自的特点，为这类问题的分析和求解提供一些参考和借鉴。
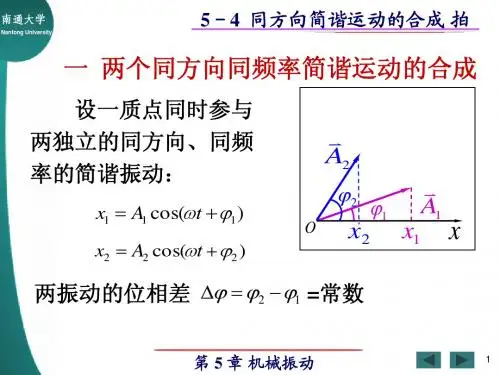
1两个同方向同频率简谐振动的合成设两个简谐振动都沿着x 轴方向振动，平衡位置都为坐标原点， 它们振动的角频率3,振幅分别为A]和A2，初相分别为®和％， 它们的振动方程分别为：x,=A| cos （（ot+（p]） x 2=A 2 cos （（ot+（p 2）求这两个解析振动的合振动。
1. 1解析法由于两个简谐振动都沿着X 轴方向振动，所以这两个简谐振动在任一时刻合振动的位移也应在X 轴方向上，且合振动的位移X 等 于这两个分振动位移的代数和，即：X=X]+x 2将分振动的方程X1和X2代入上式展开整理：x = x }+x 2= A } COS （＜zX + % ） + 厦2 COS （m + 02 ）=4 cos （p 、cos - /1] sin （p } cos cotA 2 cos （p 2 cos cot- A 2s\n （p 2 sin cut=（A, cos （p 、+ A 2 cos %） cos cot sin （p 、4- A 2 sin （p 2） sin cot 令 A cos （p=A] cos （p]+A 2 cos （p 2 A sin （p=A 1 sin （P]+A 2 sin （p 2 得至lj x=A cos （p coscot-A sin （p sin （ot=A cos （（ot+（p ）这一结果表明：两个同方向同频率简谐振动的合振动依旧是一 个简谐振动，且合振动的频率与分振动的频率相同都等于3,合振 动的振幅和初相可以表示为：A = J （/sin 0）2 +（/cos （p ）2=J A ： + / j + 2A t A 2 cos （02 - ％）川 sin 0 _ A x sin ® + A 2 sin （p 2t a n （p =------—-------------------A cos （p A x cos （p 、+ A 2 cos （p 21.2旋转矢量法如图1所示，4和力2分别为两个分振动的旋转矢量，它们以相 同的角速度绕o 点做逆时针转动，t=Os 时它们与x 轴正向的夹角分 别为卩和①。
二、振动的合成实际生活中，一个系统往往会同时参与两个或更多的振动。
例如悬挂在颠簸船舱中的钟摆，两列声波同时传入人耳等。
一般的振动合成显然是比较复杂，下面仅讨论几种间单情况的简谐振动合成。
一、同方向同频率简谐振动的合成若两个同方向的简谐振动，频率都是，它们的运动方程分别为因振动是同方向的，所以这两个谐振动在任意时刻的和位移应在同一直线上，且等于这两个振动位移的代数和，即合位移仍为简谐振动二、两个同方向不同频率简谐振动的合成拍如果两个简谐振动的振动方向相同而频率不同，那么合成后的振动仍与原振动方向相同但不再是简谐振动。
现设两简谐振动的振幅都为A，初相位为零，它们的振动方程分别为合成振动方程为若两个分振动的频率都较大且其差很小时，即，合振动可看作为振幅随时间缓慢变化的近似谐振动，振幅随时间变化且具有周期性，表现出振动或强或弱的现象，称拍，变化的频率称拍频，变化的振幅为变化的频率为三、相互垂直的简谐振动的合成李萨如图如果两个简谐振动分别在x轴和y轴上进行，他们的振动方程分别为合成后，可得质点的轨迹为椭圆方程若两分振动有不同的频率，且两频率之比为有理数时，则合成后的质点运动具有稳定、封闭的轨迹。
称其为李萨如图形。
程序编写我们已经在第一讲中体验了matlab的编程，可是你一定会生出这样的问号，辛辛苦苦在命令窗口写的一大堆代码怎么不保留？不用担心，matlab程序和其他编程工具一样，也有专门的文件格式，称m文件，文件名形式为“文件名.m”。
你可以用matlab自带的编辑器来输入你的程序代码，当然你也可以用其它编辑器或最经济的文本编辑器，不过别忘记添加文件名的后缀“.m”。
下面，请跟我一起用m文件编辑器来编写matlab程序。
例题：两个振动方向相同而频率不同的简谐振动方程分别为合成后的方程是请用matlab程序描述合成波和拍频现象。
编程：第一步：点击matlab图标，打开程序窗口。
第二步：选file—new—m-file,打开编辑器。
第七章振动和波振动与波无所不在振动与波是横跨物理学各分支学科的最基本的运动形式。
尽管在各学科里振动与波的具体内容不同，但在形式上却有很大的相似性。
振动的强弱与振幅的平方相关，这种周期变化的现象称为拍。
拍是一个重要的现象，有许多应用。
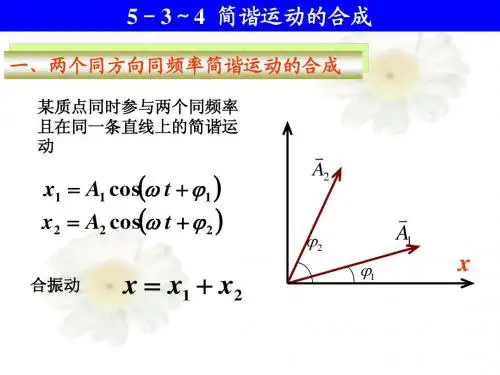
§7.1.5 方向互相垂直、不同频率简谐振动的合成当两个互相垂直的简谐振动频率不同时，合成的轨道与频率之比和两者的相位都有关系，图形一般较为复杂，很难用数学式子表达。
当两者的频率之比是有理数时合运动是周期运动，轨道是闭合的曲线或有限的曲线段这种图形称为李萨如图形（Lissajous figure）⎩⎨⎧+=+=)cos()cos(y y y x x x t A y t A x ϕωϕωx 、y 两垂直方向的简谐振动时，对应不同初相位差的李萨如图形2:1:=y x ωωxyO 相邻的李萨如图形初相位差为12°yxx y相邻的李萨如图形初相位差为12°yxx y相邻的李萨如图形初相位差为12°傅里叶级数：L L ,sin ,cos ,2sin ,2cos ,sin ,cos ,1t n t n t t t t ωωωωωω它们都具有周期T ，且有正交性和完备性∫∫∫⎩⎨⎧=≠=⎩⎨⎧=≠==T TTm n T m n tdt m t n m n T m n tdt m t n tdt m t n 000)(2/)(0sin sin )(2/)(0cos cos 0cos sin ωωωωωω正交性简谐振动的复数表示)(0ϕω+=t i Aex 复数表示的优越之处：求导、积分很方便。
)sin()cos(00)(0ϕωϕωϕω+++==+t iA t A Aex t i 复数的实部对应真实的振动量第七章作业题A组1、6、7、9、10、12、15、18、21、25、28、33、37、39、45、46、47B组48、52、55xφ0l 0l yly ⎟⎟⎠⎞不是线性回复力x =动力学方程及其解x的通解形式为2=+xxω&&)cos(ϕω+=tAx通解中包含两个待定的积分常量，它们取决于振动的初始运动状态，) ,(ϕA),(v x描述简谐振动的三个特征参量：振幅、初相位和频率固有频率ω0弹簧振子单摆复摆m k=0ωl g =0ωOOCI mgl =0ω任一振动系统的固有频率由振子的固有参量决定，与初始条件无关。
