2.2 力矩和力偶

《力矩和力偶》讲义一、引言在物理学和工程学中，力矩和力偶是两个非常重要的概念。

它们对于理解物体的旋转运动、机械系统的工作原理以及结构的稳定性都起着至关重要的作用。

接下来，让我们深入探讨一下力矩和力偶的相关知识。

二、力矩的定义和概念力矩，简单来说，就是使物体绕着某个固定点或轴转动的趋势。

它等于力与力臂的乘积。

力臂是指从转动轴到力的作用线的垂直距离。

如果用M 表示力矩，F 表示力，L 表示力臂，那么力矩的计算公式就是 M ＝ F × L 。

为了更好地理解力矩，我们可以想象一个门。

当我们在门的把手处施加一个力来推动或拉动门时，门就会绕着门轴转动。

施加的力越大，或者力臂越长，产生的力矩就越大，门就越容易转动。

在实际生活和工程应用中，力矩的概念无处不在。

例如，用扳手拧螺丝时，我们通过施加力在扳手上，利用扳手的长度（力臂）产生足够的力矩来拧紧或松开螺丝。

三、力矩的性质1、力矩的方向力矩是一个矢量，它的方向根据右手定则来确定。

伸出右手，让四指沿着力臂的方向弯曲，大拇指所指的方向就是力矩的方向。

2、合力矩定理当一个物体受到多个力的作用时，这些力对某一点的合力矩等于各个分力对同一点的力矩的代数和。

3、力矩的平衡如果一个物体处于静止状态或者绕某一轴匀速转动，那么作用在物体上的所有力矩之和为零。

这就是力矩平衡的条件。

四、力偶的定义和概念力偶是由大小相等、方向相反、但不共线的两个平行力所组成的力系。

这两个力的作用线之间的垂直距离称为力偶臂，力偶中的力与力偶臂的乘积称为力偶矩。

力偶的特点是它不能用一个单一的力来等效替代，只能产生转动效应。

例如，用两只手同时在方向盘的两侧施加方向相反、大小相等的力，方向盘就会转动，这就是力偶的作用。

五、力偶的性质1、力偶无合力由于力偶中的两个力大小相等、方向相反且不共线，所以它们的合力为零。

但这并不意味着力偶没有作用效果，它能够使物体产生纯转动。

2、力偶矩的大小和方向力偶矩的大小等于其中一个力的大小与力偶臂的乘积，其方向由力偶的转向决定。

第2章力矩与力偶2.1力对点的矩从实践中知道，力对物体的作用效果除了能使物体移动外，还能使物体转动，力矩就 是度量力使物体转动效果的物理量。

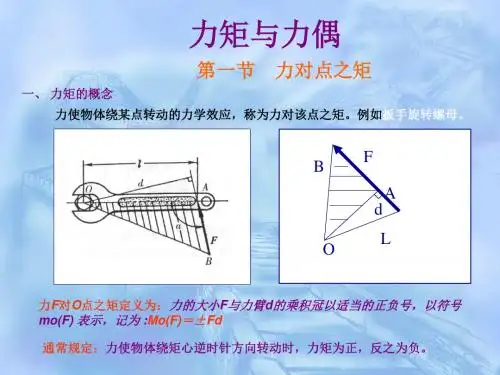
力使物体产生转动效应与哪些因素有关呢？现以扳手拧螺帽为例，如图 2.1所示。

手加在扳手上的力F ，使扳手带动螺帽绕中心 0转动。

力F 越大，转动越快；力的作用线离转动中心越远，转动也 越快；如果力的作用线与力的作用点到转动中心0点的连线不垂直，则转动的效果就差；当力的作用线通过转 动中心0时，无论力F 多大也不能扳动螺帽， 只有当力 的作用线垂直于转动中心与力的作用点的连线时，转动 效果最好。

另外，当力的大小和作用线不变而指向相反 时，将使物体向相反的方向转动。

在建筑工地上使用撬 杠抬起重物，使用滑轮组起吊重物等等也是实际的例子。

通过大量的实践总结出以下的规律：力使物体绕某点转 动的效果，与力的大小成正比，与转动中心到力的作用线的垂直距离 d 也成正比。

这个垂直距离称为力臂，转动中心称为力矩中心 (简称矩心)。

力的大小与力臂的乘积称为力F 对点0之矩(简称力矩)，记作m °(F)。

计算公式可写为m °(F)二-F d式中的正负号表示力矩的转向。

在平面内规定：力使物体绕矩心作逆时针方向转动时,力矩为正；力使物体作顺时针方向转动时，力矩为负。

因此，力矩是个代数量。

力矩的单位是N m 或kNm 。

由力矩的定义可以得到如下力矩的性质:(1)力F 对点0的矩，不仅决定于力的大小，同时与矩心的位置有关。

矩心的位置不 同，力矩随之不同;(2)当力的大小为零或力臂为零时，则力矩为零；⑶力沿其作用线移动时，因为力的大小、方向和力臂均没有改变，所以，力矩不变。

(4)相互平衡的两个力对同一点的矩的代数和等于零。

例2.1分别计算图2.2中F ,、F 2对0点的力矩。

解 从图2 - 2中可知力F 1和F 2对0点的力臂是h 和|2。

(2.1)\P图2, 1故 m °(F)= ± F i l 1 = F i l 1 sin30° =49 X 0.1 X 0.5=2.45N.mm o(F)= ± F 2 l 2 = — F 2 l 2 = — 16.3 X0.15=2.45N.m必须注意：一般情况下力臂并不等于矩心与 力的作用点的距离，女口F 1的力臂是h ，不是11 。

力矩和力偶-人教版选修2-2教案一、教学目标1.了解力矩和力偶的概念，理解它们的物理意义。

2.学会计算力矩和力偶。

3.学习如何应用力矩和力偶解决实际问题。

二、教学重难点1.理解力矩和力偶的概念。

2.掌握力矩和力偶的计算方法。

3.能够应用力矩和力偶解决实际问题。

三、教学内容1. 力矩的概念力矩是描述力对物体产生扭转效应的物理量。

当一个力作用于物体上时，它可能会引起物体旋转，这个旋转的效应就称为力矩。

力矩的大小等于力乘以力臂，力臂是力作用点到物体旋转中心的距离。

2. 力偶的概念力偶是两个大小相等、方向相反的力在同一直线上并分别作用于物体的两个点上时产生的物理效应。

力偶的大小等于其中一个力的大小乘以两个力的距离，方向垂直于该直线。

3. 力矩和力偶的计算公式•力矩的计算公式：$M = F \\times L$，其中M表示力矩，F表示作用力的大小，L表示力臂的长度。

•力偶的计算公式：$T = F \\times d$，其中T表示力偶，F表示其中一个力的大小，d表示两个力的距离。

4. 力矩和力偶的应用(1) 物体平衡问题物体平衡条件是所有受力和力矩都为零。

在处理物体平衡问题时，可以通过计算受力点数矩的和来确定力是否平衡。

如果受力点数矩为零，则物体受到的所有力矩相互抵消，物体处于平衡状态。

(2) 固定点和支撑点固定点是物体旋转中心，支撑点是受力的点。

在处理力矩和力偶的问题时，需要明确固定点或支撑点的位置，才能正确计算力矩和力偶。

(3) 机械设备设计在机械设备的设计中，经常需要考虑力矩和力偶。

比如，在机器人的关节处需要合理分布力矩，以保证机器人能够移动和控制。

四、教学方法本节课采用讲授和案例分析相结合的教学方法来讲解力矩和力偶的概念和计算方法。

在讲解理论的同时，结合实际应用，通过案例分析来加深学生对力矩和力偶的理解和掌握。

五、教学评价本节课采用理论讲解和案例分析相结合的教学方法，能够让学生更好地理解和掌握力矩和力偶的概念和计算方法。

《力矩和力偶》讲义在物理学和工程学中，力矩和力偶是两个非常重要的概念。

它们在理解物体的转动和平衡等方面起着关键作用。

接下来，让我们深入了解一下力矩和力偶。

一、力矩力矩，简单来说，就是使物体转动的能力。

想象一下，你试图用扳手拧松一个螺丝。

当你在扳手的一端施加一个力时，这个力能够使螺丝转动，而衡量这个转动效果的物理量就是力矩。

力矩的大小等于力的大小乘以力臂的长度。

力臂是从转动轴到力的作用线的垂直距离。

如果用 M 表示力矩，F 表示力，L 表示力臂，那么力矩的计算公式就是 M ＝ F × L 。

例如，一个力为 10N，作用点距离转动轴 2m，力臂就是 2m，那么力矩就是 10×2 ＝ 20N·m 。

力矩的方向遵循右手定则。

伸出右手，让四指沿着力绕轴转动的方向弯曲，那么大拇指所指的方向就是力矩的方向。

在实际生活中，力矩有很多应用。

比如开门时，我们在门把手上施加一个力，通过长长的力臂产生较大的力矩，从而轻松地把门打开。

二、力偶力偶是由两个大小相等、方向相反、但不在同一直线上的平行力所组成的系统。

这两个力的合力为零，但它们能够使物体产生转动。

力偶的作用效果仅仅取决于力偶矩的大小和方向，而与力偶中两个力的作用点的位置无关。

力偶矩等于其中一个力的大小乘以两个力之间的垂直距离，即力偶臂。

假设力偶中的两个力大小都为 F ，力偶臂为 d ，那么力偶矩 M 就等于 F × d 。

力偶在工程和日常生活中也很常见。

比如，用两个手指拧动螺丝帽，或者汽车的方向盘在转动时，都是力偶在起作用。

三、力矩与力偶的关系力矩和力偶既有联系又有区别。

联系在于，力偶可以看成是由一对特殊的力矩组成，这对力矩的大小相等、方向相反，且都作用在同一物体上。

区别在于，力矩是单个力对物体转动效果的度量，而力偶是两个力的组合对物体转动效果的度量。

此外，单个力矩可以使物体产生转动和平动，而力偶只能使物体产生纯转动。

四、力矩和力偶的平衡当一个物体处于平衡状态时，作用在它上面的所有力矩和力偶的总和必须为零。

力偶矩和力矩一、力偶矩的定义和概念1.1 力偶的概念力偶是由两个大小相等、方向相反的力构成的力对，它们的作用线平行但不共线。

力偶可用一个力矩矢量来表示，该矢量的大小等于其中一个力的大小乘以它们之间的距离，方向垂直于作用线，符合右手定则。

1.2 力偶矩的定义力偶矩是力偶对物体所产生的力矩，它描述了力偶对物体的“扭转”效果。

力偶矩的大小等于力偶矩矢量与力偶矩臂之间的夹角的正弦值乘以力偶的大小。

二、力矩的定义和性质2.1 力矩的定义力矩是描述力对物体产生“转动效果”的物理量。

力矩的大小等于力的大小与作用力臂之间的乘积，方向垂直于力矢量和作用力臂所在的平面，符合右手定则。

2.2 力矩的性质•力矩与力的大小和力臂长度成正比。

•作用在刚体上的一组力的合力矩等于各个力矩的矢量和。

•如果合外力矩为零，则刚体处于平衡状态。

三、力偶矩和力矩的关系3.1 力偶矩和力矩的相似性力偶矩和力矩在物理学中有很多相似之处。

它们都描述了力对物体的“扭转”效果，都与力的大小、作用线和作用力臂有关。

力偶矩和力矩都可以用矢量来表示，且方向垂直于力的作用线和作用力臂所在的平面。

3.2 力偶矩的计算方法对于一个力偶，可以通过计算其中一个力的力矩再乘以其距离来得到力偶矩的大小。

力偶矩的方向垂直于力的作用线，遵循右手定则。

3.3 力偶矩和力矩的关系可以发现，力偶矩可以被看作是一种特殊的力矩。

力偶可以看作是由两个大小相等、方向相反的力构成的力对，而力矩是由一个单一的力对物体产生的扭转效果。

力偶矩的计算方法与力矩一致，只是力偶矩的距离是两个力之间的距离。

两者都可以用矢量来表示，并且方向都垂直于力的作用线和作用力臂所在的平面。

四、力偶矩和力矩在实际中的应用4.1 力偶矩的应用•力偶矩常被应用于刚体平衡问题的分析中，用于计算刚体所受到的力矩以及刚体的平衡条件。

•力偶矩也常用于描述弹簧力和扭矩等力学现象。

•在工程领域，力偶矩的概念被广泛应用于机械设计和结构分析中，用于计算物体的稳定性和强度等参数。