力矩力偶矩

力矩和力偶矩的概念力矩和力偶矩是物理学中的基本概念，它们在机械、力学等领域中应用广泛。

下面将详细地介绍它们的含义和相关概念。

一、力矩力矩，也称为力臂矩，是指力在某一点的偏转能力，即力通过某一点产生的旋转效应。

在物理学中，力矩的计算公式为：M=F*d，其中M 表示力矩，F表示作用力，d表示作用力对应的力臂。

通常我们用N·m 来表示力矩的单位。

力矩的方向与力的方向垂直，遵循右手定则，即以力为轴心，右手四指指向力的方向，拇指的方向就是力矩的方向。

下面简单介绍一下力矩的几种类型：1. 静止力矩：当物体处于静止状态时，力的作用点到旋转轴的距离与力的大小乘积就是静止力矩。

静止力矩越大，物体的旋转就越困难。

2. 动态力矩：当物体处于运动状态时，动态力矩就是作用在物体上的动态力量产生的效应。

动态力矩通常通过对物体的角加速度进行计算得出。

3. 平衡力矩：在物体处于平衡状态时，所有的力矩相互抵消，这些力矩被称为平衡力矩。

判断物体是否处于平衡状态时，可以通过计算平衡力矩来得出结论。

4. 转动惯量：在计算力矩时，还需要用到转动惯量的概念。

转动惯量是物体绕一个轴旋转时所需要的力矩与角加速度之比。

通常我们用kg·m2表示转动惯量的单位。

二、力偶矩力偶矩，也称为耦合力矩，是指通过两个相等作用力产生的旋转效应。

力偶矩的大小等于两个相等作用力的大小乘积再乘以它们之间的距离。

力偶矩的方向垂直于作用力的方向，并且遵循右手定则。

下面简单介绍一下力偶矩的几种性质：1. 力偶矩平面：将力偶矩所产生的旋转轴称为力偶矩平面。

通常情况下，力偶矩平面是由两个作用力之间的连线和它们施加力的垂线所构成的。

2. 产生力偶矩的条件：只有在作用力方向相反、大小相等，并且在同一平面内的两个力才能产生力偶矩。

3. 力偶矩的效应：力偶矩可以使物体产生旋转效应，但同时也会改变物体的转动惯量。

因此，力偶矩会对物体的旋转产生影响。

总之，力矩和力偶矩是物理学中非常重要的概念。

力矩力偶矩力矩是物理学中的一个重要概念，它是描述对物体产生转动效果的度量单位。

而力偶矩则是力矩的一种特殊情况，它是发生在两个反向力相等但作用线不在同一条直线上的情况下的力矩。

在物理学和工程学中，力矩和力偶矩是重要的基本理论，它们在机械学、工业生产和航空航天等领域中有广泛的应用。

下面我们将分步骤阐述力矩和力偶矩的定义和计算方法：1. 力矩的定义：力矩是一个物体绕某一点进行旋转的趋势，其大小等于作用力与力臂的乘积。

力臂是指力作用线与选择的旋转轴之间的垂直距离。

根据符号规定，当力的作用方向与力臂的方向所成角度小于180度时，力矩为正；反之，力矩为负。

式子表示为：M = F × d，其中M表示力矩，F表示作用力，d表示力臂。

2. 力偶矩的定义：力偶矩是指两个相等但方向相反的力作用在物体上所产生的力矩。

计算力偶矩时，需要考虑两个力矢量之间的距离，即力臂，力偶矩的方向垂直于两个力矢量所在平面，并沿着它们的叉积方向。

式子表示为：L = F × a，其中L表示力偶矩，F表示两个相等的作用在物体上的力，a表示它们之间的距离。

3. 力矩和力偶矩的应用：在工程学中，力矩和力偶矩的应用广泛，例如在机械学中，力矩用于描述机械运动，例如发动机和汽车传动系统。

而在钢筋加工中，力偶矩用于解决弯曲和扭曲的问题。

在航空航天中，力矩和力偶矩则用于计算飞机和导弹的舵面和气动布局等问题。

总结：力矩和力偶矩是物理学中重要的概念，它们在机械学、工业生产和航空航天等领域中有重要的应用。

在实际应用中，我们需要了解力矩和力偶矩的定义、计算方法和应用，以便正确应用这些理论，解决各种实际问题。

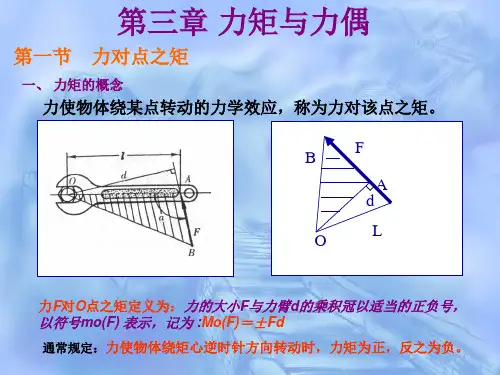
力矩力偶的概念一、概念介绍力矩和力偶是力学中的重要概念，用于描述物体受到的转动效应。

力矩是由一个力在物体上产生的旋转效果，而力偶则是由两个相等大小、方向相反的力所产生的旋转效果。

二、力矩的定义与计算1. 定义：力矩是指一个作用在物体上的力对该物体产生旋转效应的量度。

2. 计算：力矩等于作用在物体上的力与该力距离物体某一点（通常为旋转中心）的垂直距离之积。

即M = Fd，其中M为力矩，F为作用在物体上的力，d为该力距离旋转中心的垂直距离。

三、影响因素1. 力大小：当施加于物体上的外部作用力增大时，其所产生的旋转效应也会增大。

2. 作用点位置：当外部作用点远离旋转中心时，其所产生的旋转效应也会增大。

3. 旋转中心位置：当旋转中心移动到距外部作用点更远处时，其所产生的旋转效应也会增大。

1. 机械工程：力矩被广泛应用于机械工程中，例如在汽车发动机的设计中，需要计算发动机输出的扭矩大小，以及通过传动系统将扭矩传递到车轮上。

2. 物理学：力矩被用于解释天体运动和物体旋转的现象，例如地球公转和自转、陀螺运动等。

3. 运动学分析：力矩可以用于分析人体运动时的肌肉力量作用，例如在举重运动中，需要计算出各个关节处所受到的力矩大小。

五、力偶的定义与计算1. 定义：力偶是由两个相等大小、方向相反的力所产生的旋转效应。

2. 计算：力偶等于两个相等大小、方向相反的力之间距离（称为臂长）之积。

即C = Fd，其中C为力偶大小，F为每个作用在物体上的相等大小、方向相反的力，d为两个作用点之间距离。

六、影响因素1. 力大小：当施加于物体上的外部作用力增大时，其所产生的旋转效应也会增大。

2. 作用点位置：当外部作用点远离旋转中心时，其所产生的旋转效应也会增大。

3. 两个作用点之间的距离：当两个作用点之间的距离增大时，其所产生的旋转效应也会增大。

1. 物理学：力偶被广泛应用于解释天体运动和物体旋转的现象，例如在行星公转和自转、陀螺运动等。

1、力矩是一个向量，可以被想象为一个旋转力或角力，导致出旋转运动的改变的力力偶是作用于同一刚体上的一对大小相等、方向相反、但不共线的一对平行力，可以理解为力矩的代数和。

2、力偶中两个力之间的垂直距离d 称为力偶臂。

3、力偶中的力F与力偶臂d 的乘积称为力偶矩。

4、他两的区别是力偶就只有两个方向,力距可以多个力多个方向。

5、力偶矩与力矩的区别是力矩的大小、正负与力和矩心的相对位置有关；力偶对任一点之矩均等于力偶矩。

力偶矩可以完全描述一个力偶；力对点之矩不能完全描述一个力偶。

6、力矩在物理学里是指作用力使物体绕着转动轴或支点转动的趋向。

力矩的单位是牛顿-米。

力矩希腊字母是tau。

力矩的概念，起源于阿基米德对杠杆的研究。

转动力矩又称为转矩或扭矩。

力矩能够使物体改变其旋转运动。

推挤或拖拉涉及到作用力，而扭转则涉及到力矩。

力矩等于径向矢量与作用力的叉积。

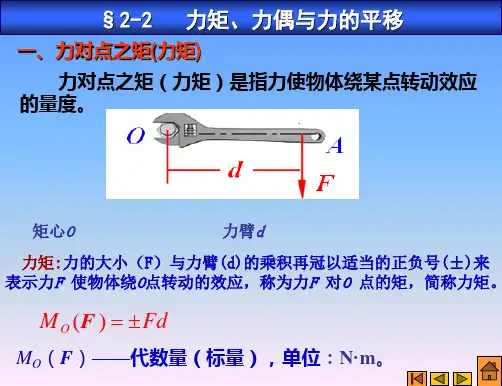
力偶矩和力矩力偶矩和力矩是力学中两个重要的概念，它们在研究物体的平衡和力的作用时起到了重要的作用。

本文将分别介绍力偶矩和力矩的概念以及它们的应用。

一、力偶矩力偶矩是指由两个大小相等、方向相反的力组成的力对所产生的力矩。

在物理学中，力偶矩通常用于描述物体的平衡状态。

当一个物体受到一个力偶矩时，如果物体不受任何其他力的作用，它将保持在平衡状态。

具体来说，假设有两个大小相等、方向相反的力分别作用在物体的两个不同点上，这两个力之间的连线被称为力的作用线。

力偶矩的大小等于其中一个力的大小乘以它们之间的距离，方向垂直于力的作用线。

力偶矩的计算公式可以表示为M = F * d，其中M表示力偶矩，F表示力的大小，d表示力的作用线之间的距离。

力偶矩在实际应用中具有广泛的应用。

例如，在建筑工程中，施工人员常常需要使用力偶矩来计算柱子或梁的平衡状态。

通过施加一个合适大小和方向的力偶矩，可以使得柱子或梁保持平衡，从而确保建筑结构的稳定性。

二、力矩力矩是指力对物体产生的转动效应。

当一个物体受到一个力时，力矩决定了物体的转动情况。

力矩的大小等于力的大小乘以力臂，力臂是力作用点到物体转轴的垂直距离。

力矩的计算公式可以表示为M = F * r，其中M表示力矩，F表示力的大小，r表示力臂的长度。

力矩的方向遵循右手螺旋法则，即当右手握住力臂时，拇指所指的方向即为力矩的方向。

力矩在实际应用中也有广泛的应用。

例如，在机械工程中，设计师常常需要使用力矩来计算机械装置的平衡状态。

通过施加一个合适大小和方向的力矩，可以使得机械装置保持平衡，从而确保其正常运转。

三、力偶矩和力矩的关系力偶矩和力矩在概念上是相似的，都与力的转动效应有关。

然而，它们在应用上有一些区别。

力偶矩是由两个大小相等、方向相反的力组成的，而力矩是由一个力产生的。

力偶矩由于有两个力的作用，因此具有更强的转动效应。

力偶矩的作用线是两个力之间的连线，而力矩的作用线是力的作用点到物体转轴的连线。

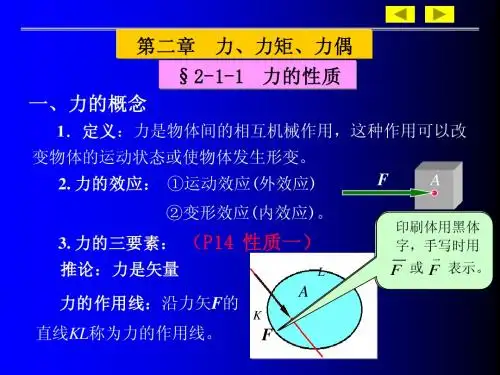
力偶矩和力矩一、力偶矩的定义和概念1.1 力偶的概念力偶是由两个大小相等、方向相反的力构成的力对，它们的作用线平行但不共线。

力偶可用一个力矩矢量来表示，该矢量的大小等于其中一个力的大小乘以它们之间的距离，方向垂直于作用线，符合右手定则。

1.2 力偶矩的定义力偶矩是力偶对物体所产生的力矩，它描述了力偶对物体的“扭转”效果。

力偶矩的大小等于力偶矩矢量与力偶矩臂之间的夹角的正弦值乘以力偶的大小。

二、力矩的定义和性质2.1 力矩的定义力矩是描述力对物体产生“转动效果”的物理量。

力矩的大小等于力的大小与作用力臂之间的乘积，方向垂直于力矢量和作用力臂所在的平面，符合右手定则。

2.2 力矩的性质•力矩与力的大小和力臂长度成正比。

•作用在刚体上的一组力的合力矩等于各个力矩的矢量和。

•如果合外力矩为零，则刚体处于平衡状态。

三、力偶矩和力矩的关系3.1 力偶矩和力矩的相似性力偶矩和力矩在物理学中有很多相似之处。

它们都描述了力对物体的“扭转”效果，都与力的大小、作用线和作用力臂有关。

力偶矩和力矩都可以用矢量来表示，且方向垂直于力的作用线和作用力臂所在的平面。

3.2 力偶矩的计算方法对于一个力偶，可以通过计算其中一个力的力矩再乘以其距离来得到力偶矩的大小。

力偶矩的方向垂直于力的作用线，遵循右手定则。

3.3 力偶矩和力矩的关系可以发现，力偶矩可以被看作是一种特殊的力矩。

力偶可以看作是由两个大小相等、方向相反的力构成的力对，而力矩是由一个单一的力对物体产生的扭转效果。

力偶矩的计算方法与力矩一致，只是力偶矩的距离是两个力之间的距离。

两者都可以用矢量来表示，并且方向都垂直于力的作用线和作用力臂所在的平面。

四、力偶矩和力矩在实际中的应用4.1 力偶矩的应用•力偶矩常被应用于刚体平衡问题的分析中，用于计算刚体所受到的力矩以及刚体的平衡条件。

•力偶矩也常用于描述弹簧力和扭矩等力学现象。

•在工程领域，力偶矩的概念被广泛应用于机械设计和结构分析中，用于计算物体的稳定性和强度等参数。