力矩和力偶

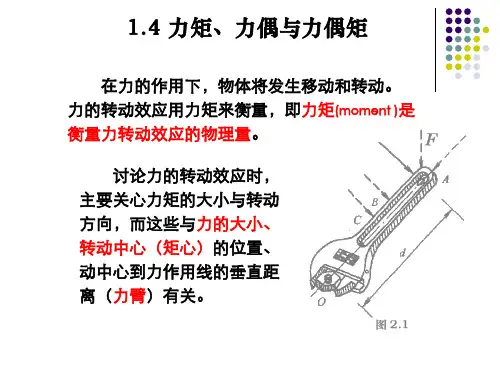
第2章力矩与力偶2.1力对点的矩从实践中知道，力对物体的作用效果除了能使物体移动外，还能使物体转动，力矩就 是度量力使物体转动效果的物理量。

力使物体产生转动效应与哪些因素有关呢？现以扳手拧螺帽为例，如图 2.1所示。

手加在扳手上的力F ，使扳手带动螺帽绕中心 0转动。

力F 越大，转动越快；力的作用线离转动中心越远，转动也 越快；如果力的作用线与力的作用点到转动中心0点的连线不垂直，则转动的效果就差；当力的作用线通过转 动中心0时，无论力F 多大也不能扳动螺帽， 只有当力 的作用线垂直于转动中心与力的作用点的连线时，转动 效果最好。

另外，当力的大小和作用线不变而指向相反 时，将使物体向相反的方向转动。

在建筑工地上使用撬 杠抬起重物，使用滑轮组起吊重物等等也是实际的例子。

通过大量的实践总结出以下的规律：力使物体绕某点转 动的效果，与力的大小成正比，与转动中心到力的作用线的垂直距离 d 也成正比。

这个垂直距离称为力臂，转动中心称为力矩中心 (简称矩心)。

力的大小与力臂的乘积称为力F 对点0之矩(简称力矩)，记作m °(F)。

计算公式可写为m °(F)二-F d式中的正负号表示力矩的转向。

在平面内规定：力使物体绕矩心作逆时针方向转动时,力矩为正；力使物体作顺时针方向转动时，力矩为负。

因此，力矩是个代数量。

力矩的单位是N m 或kNm 。

由力矩的定义可以得到如下力矩的性质:(1)力F 对点0的矩，不仅决定于力的大小，同时与矩心的位置有关。

矩心的位置不 同，力矩随之不同;(2)当力的大小为零或力臂为零时，则力矩为零；⑶力沿其作用线移动时，因为力的大小、方向和力臂均没有改变，所以，力矩不变。

(4)相互平衡的两个力对同一点的矩的代数和等于零。

例2.1分别计算图2.2中F ,、F 2对0点的力矩。

解 从图2 - 2中可知力F 1和F 2对0点的力臂是h 和|2。

(2.1)\P图2, 1故 m °(F)= ± F i l 1 = F i l 1 sin30° =49 X 0.1 X 0.5=2.45N.mm o(F)= ± F 2 l 2 = — F 2 l 2 = — 16.3 X0.15=2.45N.m必须注意：一般情况下力臂并不等于矩心与 力的作用点的距离，女口F 1的力臂是h ，不是11 。

力矩和力偶
力矩和力偶是力学中的两个基本概念，它们在力的作用方式和使用效果上存在一些区别。

力矩是一个向量，它描述了力对物体产生转动作用的效果，是力对某一轴线或点的作用力矩。

力矩的大小等于力的大小和其到旋转轴或点的距离的乘积，方向垂直于轴或点。

在计算上，力矩等于力与力臂的乘积，其中力臂是从旋转轴或点到力的作用线的垂直距离。

力偶是一对大小相等、方向相反且不共线的平行力，它们的作用效果是使物体产生转动。

这对力在相互垂直的平面上，其中一个力垂直于这个平面，另一个力平行于这个平面。

在实际应用中，力偶可以用来转动锁紧物体，例如螺栓、螺母等。

综上所述，力矩和力偶虽然都涉及到力的作用，但它们的作用方式和使用效果有所不同。

力矩描述的是力对物体产生转动作用的效果，而力偶则是一种产生转动作用的特殊方式。

力偶力矩力偶矩之间的关系
力偶矩、力矩和力偶之间存在以下关系：
- 力矩是一个描述力的转动效果的物理量，它的大小等于力的大小与力臂的乘积，方向垂直于力和力臂所在的平面，是一个矢量。

力臂是从转动轴到力的垂直距离，是描述转动效果的关键因素。

- 力偶是一个成对出现的力，它们等大、反向、作用在同一直线上，但不共点。

力偶矩是描述力偶的转动效果的物理量，它的大小等于力偶中两个力的大小和它们的力臂的乘积，方向垂直于力和力臂所在的平面，也是一个矢量。

- 力偶矩和力矩的区别在于，力矩的大小、正负与力和矩心的相对位置有关；而力偶矩与转动轴的位置无关。

总之，力偶矩、力矩和力偶是描述力的不同物理量，它们的大小、方向和作用效果均有所不同。

在实际应用中，需要根据具体情况选择合适的物理量来描述力的作用。

物理学中的力矩与力偶力矩和力偶是物理学中的重要概念，它们在解析力学和刚体运动方面有着广泛的应用。

本文将会从力矩和力偶的概念入手，讨论它们的物理意义和应用。

力矩是物理学中用来描述力对物体产生的转动效应的物理量。

它是由力的大小和作用点到旋转轴的距离决定的。

具体而言，力矩等于力的大小乘以力臂，力臂是力作用在物体上的垂直距离，力矩的方向由右手螺旋法则确定。

（需要注意的是，由于无法绘制图像，我将无法在文章中插入示意图，但希望您能够通过文字来理解描述）力矩在物理学中有很多应用，特别是在解析力学中。

通过计算物体上的力矩，可以确定物体是否会发生平衡或转动。

在静力学中，力矩的和为零时，物体处于平衡状态。

这是因为在平衡状态下，物体上的所有力矩相互抵消。

而当力矩和不为零时，物体将发生转动。

通过严谨的计算和分析，可以准确地预测物体的旋转。

除了力矩，力偶也是解析力学中的一个重要概念。

力偶是由两个大小相等、方向相反的力构成的，它们作用在物体的不同点上。

力偶的特点是产生一个对称的转动效应，因为两个力的大小和方向相等，但作用点不同，所以它们在物体上产生的力矩相等但方向相反。

力偶的应用十分广泛，特别在刚体的平衡分析中。

当物体受到一个平行于旋转轴的力偶时，该物体将保持平衡。

这是因为力偶使物体上的所有力矩相互抵消，使物体不发生任何旋转。

这个原理在机械平衡中有着广泛的应用。

例如，在一个平衡的悬臂上悬挂一个负载，在给定的力等于负载重量的情况下，该负载将保持平衡，不会倾斜或旋转。

这种力偶平衡可以通过计算力矩和来证明。

除了上述的应用，力矩和力偶还在其他领域有广泛的应用。

例如，力矩和力偶在工程设计中起着关键作用。

在建筑设计中，力矩和力偶的应用可以帮助工程师确定材料的承受能力，确保建筑物的结构稳定和安全。

在机械设计中，力矩和力偶的计算可以用于确定机械部件的强度和稳定性。

综上所述，力矩和力偶在物理学中有着重要的地位和广泛的应用。

它们不仅在解析力学中发挥着重要作用，还在工程设计和机械设计等领域有着广泛的应用。

工程力学中的力矩与力偶分析工程力学是一门研究物体受力和作用力的学科，其中力矩与力偶是重要的概念与分析方法。

力矩是力的旋转效果，力偶则是由一对大小相等、方向相反的力构成，它们在工程力学中有着广泛的应用。

一、力矩的概念和计算方法力矩是衡量力的旋转效果的物理量，它描述了力对物体的转动影响。

在工程力学中，力矩的计算方法可以通过以下公式得到：M = F * d其中，M表示力矩，F表示作用力的大小，d表示作用力与旋转中心之间的距离。

根据右手定则，力矩的方向垂直于力的方向和d的方向。

力矩的计算可以分为静力矩和动力矩。

静力矩指的是静止物体受到的力矩，可以通过将物体划分为若干个力的作用点与旋转中心所连接的有无数个线段，然后将每个力的大小乘以其所对应的线段长度再求和得到。

而动力矩指的是动力学过程中物体受到的力的时间积分。

二、力偶的概念和特点力偶是由一对大小相等、方向相反的力构成的力对，它们具有相同的力臂，而力臂是力偶的重要特点之一。

力臂是指力偶成对的两个力的作用线之间的距离，力偶的力臂相等且方向相反。

力偶与力矩的区别在于，力偶是由两个力构成的力对，其作用线重合，而力矩是由单个力与旋转中心构成的，其作用线不重合。

力偶的特点使其在工程力学中被广泛应用于杆件受力分析、结构分析等领域。

三、力矩与力偶在工程力学中的应用1. 杆件受力分析：力矩与力偶常用于杆件受力分析中。

通过计算力对杆件的力矩和力偶，可以确定杆件上不同部位的受力情况，从而为工程设计提供依据。

例如，在悬臂梁的分析中，力矩与力偶的运用可以帮助工程师确定悬臂梁上的最大弯曲应力点，从而合理设计悬臂梁的支撑结构。

2. 结构分析：在结构分析中，力矩与力偶也起着重要的作用。

通过力矩与力偶的计算，可以确定结构中不同部位的受力情况，进而判断结构的稳定性。

例如，在桥梁的设计中，通过计算桥梁支点处的力矩和力偶，可以评估桥梁的承载能力，及时发现结构中存在的问题并采取相应的加固措施。

3. 机械运动分析：在机械工程中，力矩与力偶的分析也被广泛应用于机械运动的研究。

力偶矩和力矩
力偶矩和力矩是物理学中的两个重要概念，它们在力学、机械学等领
域中有着广泛的应用。

力偶矩和力矩的概念虽然相似，但是它们的物
理意义和计算方法却有所不同。

力偶矩是指两个大小相等、方向相反的力在同一平面内作用于同一点
上所产生的力矩。

力偶矩的大小等于两个力的大小乘以它们之间的距离，方向垂直于力所在的平面，符合右手定则。

力偶矩的物理意义是
描述力对物体的扭矩作用，它可以用来计算物体的旋转运动。

力矩是指力对物体产生的转动效应，它等于力的大小乘以力臂的长度。

力臂是指力作用点到物体的旋转轴的垂直距离。

力矩的方向垂直于力
臂和力的平面，符合右手定则。

力矩的物理意义是描述力对物体的转
动效应，它可以用来计算物体的平衡状态和旋转运动。

在实际应用中，力偶矩和力矩常常被用来计算物体的平衡状态和旋转
运动。

例如，在机械设计中，我们需要计算物体所受的力偶矩和力矩，以确定物体的平衡状态和旋转运动。

在航空航天领域中，力偶矩和力
矩也被广泛应用于飞行器的设计和控制中。

总之，力偶矩和力矩是物理学中的两个重要概念，它们在力学、机械
学等领域中有着广泛的应用。

了解力偶矩和力矩的概念和计算方法，对于理解物体的平衡状态和旋转运动有着重要的意义。