三角形四心讲义(学生版)

三角形“四心”问题一、三角形的“重心”1、重心的定义：中线的交点，重心将中线长度分成2:1三角形中线向量式：AM ⃗⃗⃗⃗⃗⃗ =12(AB⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ) 2、重心的性质：（1）重心到顶点的距离与重心到对边中点的距离之比为2:1。

（2）重心和三角形3个顶点组成的3个三角形面积相等。

（3）在平面直角坐标系中，重心的坐标是顶点坐标的算术平均数，即(x A +x B +x C 3,y A +y B +y C3).3、常见重心向量式：设O 是∆ABC 的重心，P 为平面内任意一点 ①OA⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =0⃗ ②PO⃗⃗⃗⃗⃗ =13(PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ ) ③若AP⃗⃗⃗⃗⃗ =λ(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )或OP ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +λ(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )，λ∈[0,+∞)，则P 一定经过三角形的重心 ④若AP ⃗⃗⃗⃗⃗ =λ(AB ⃗⃗⃗⃗⃗ |AB ⃗⃗⃗⃗⃗ |sinB +AC ⃗⃗⃗⃗⃗ |AC ⃗⃗⃗⃗⃗ |sinC )或OP ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +λ(AB ⃗⃗⃗⃗⃗ |AB ⃗⃗⃗⃗⃗ |sinB +AC⃗⃗⃗⃗⃗ |AC ⃗⃗⃗⃗⃗ |sinC )，λ∈[0,+∞)，则P 一定经过三角形的重心二、三角形的“垂心”1、垂心的定义：高的交点。

锐角三角形的垂心在三角形内； 直角三角形的垂心在直角顶点上； 钝角三角形的垂心在三角形外。

2、常见垂心向量式：O 是∆ABC 的垂心，则有以下结论： 1、OA⃗⃗⃗⃗⃗ ∙OB ⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗ ∙OC ⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ ∙OA ⃗⃗⃗⃗⃗ 2、|OA⃗⃗⃗⃗⃗ |2+|BC ⃗⃗⃗⃗⃗ |2=|OB ⃗⃗⃗⃗⃗ |2+|CA ⃗⃗⃗⃗⃗ |2=|OC ⃗⃗⃗⃗⃗ |2+|AB ⃗⃗⃗⃗⃗ |2 3、动点P 满足OP ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +λ(AB ⃗⃗⃗⃗⃗|AB ⃗⃗⃗⃗⃗ |cosB +AC ⃗⃗⃗⃗⃗|AC ⃗⃗⃗⃗⃗ |cosC )，λ∈(0,+∞)，则动点P 的轨迹一定通过∆ABC 的垂心4、奔驰定理推论：S ∆BOC :S ∆COA :S ∆AOB =tanA:tanB:tanC ，tanA ∙OA ⃗⃗⃗⃗⃗ +tanB ∙OB⃗⃗⃗⃗⃗ +tanC ∙OC ⃗⃗⃗⃗⃗ =0⃗ . 三、三角形的“内心”1、内心的定义：角平分线的交点(或内切圆的圆心)。

图3图4三角形的“四心”三角形是最重要的基本平面图形，很多较复杂的图形问题可以化归为三角形的问题.如图1 ，在三角形△ABC 中，有三条边,,AB BC CA ，三个顶点,,A B C ，在三角形中，角平分线、中线、高（如图2）是三角形中的三种重要线段.一、三角形的重心三角形的三条中线相交于一点，这个交点称为三角形的重心. 1、三角形的三条中线必交于一点1.已知：如图3中△ABC 的两条中线AD 、BE 相交于点O ，连结并延长CO ，交AB 于点F 。

求证：AF=CF证明：延长OF 到点G ，使OG=OC ∵OG=OC, ∴点O 是CG 的中点又∵点D 是BC 的中点 ∴OD 是△BGC 的一条中位线 ∴AD ∥BG ∵点O 是CG 的中点，点E 是AC 的中点 ∴OE 是△CGA 的一条中位线 ∴BE ∥AG∵AD ∥BG ，BE ∥AG ,∴四边形AOBG 是平行四边形 ∴AB 、OG 互相平分,∴AF=CF2、三角形重心的性质(1).重心到顶点的距离与重心到对边中点的距离之比为2：1。

(2).重心和三角形3个顶点组成的3个三角形面积相等。

例1：如图4中，已知三角形的一边和重心，你能找到三角形的第三个顶点吗?请你画出它的位置。

图1图2图5图6三角形的三条高线相交于一点，这个交点称为三角形的垂心. 1、三角形的三条高必交于一点已知：如图5中△ABC 中，AD 、BE 是两条高，AD 、BE 交于点O ，连接CO 并延长交AB 于点F 求证：CF ⊥AB证明：连接DE ∵∠ADB=∠AEB=90°,且在AB 同旁，∴A 、B 、D 、E 四点共圆 ∴∠ADE=∠ABE （同弧上的圆周角相等） ∵∠EAO=∠DAC,∠AEO=∠ADC=90°∴△AEO ∽△ADC ∴AE/AD=AO/AC 即AE/AO=AD/AC ∴ΔEAD ∽ΔOAC ∴∠ACF=∠ADE=∠ABE 又∵∠ABE+∠BAC=90° ∴∠ACF+∠BAC=90° ∴CF ⊥AB2、三角形垂心的性质(1).锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外(2).△ABC 中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AO·OD=BO ·OE=CO ·OF例2：如图6，点H 是等腰△ABC 的垂心，在底边BC 长度不变的情况下，顶点A 到底边BC 的距离变化时，乘积HBC ABC S S ∆∆⋅的值是否变化？证明你的结论.图7图8图9三角形的三条内角平分线相交于一点，这个交点称为三角形的内心. 1、三角形的三条内角平分线必交于一点己知：如图7，在△ABC 中，∠A 与∠B 的角平分线交于点O ，连接OC求证：OC 平分∠ACB 证明：过O 点作OD,OE,OF 分别垂直于BC,AC,AB,垂足分别为D,E,F∵AO 平分∠BAC,∴OE=OF ；∵BO 平分∠ABC,∴OD=OF ；∴OD=OE ∴O 在∠ACB 角平分线上 ∴CO 平分∠ACB2、三角形内心的性质(1).三角形的内心到三边的距离相等，都等于三角形的内切圆半径r ，cb a S r ABC++=∆2(2).在Rt △ABC 中，∠C=90°，2cb a r -+=． (3).∠BOC = 90 °+∠A/2， ∠BOA = 90 °+∠C/2， ∠AOC = 90 °+∠B/2例3：已知：如图8，在△ABC 中，∠C=90°，∠A 和∠B 的平分线相交于P 点，PE ⊥AB 于E 点，BC=3，AC=4，求BE AE ⋅的值.例4：已知：如图9，△ABC 三边长分别为,,BC a AC b AB c ===，I 为△ABC 的内心，且I 在△ABC 的边B C A CA B 、、上的射影分别为D E F 、、，求证：2b c aAE AF +-==.图10四、三角形的外心三角形三边的垂直平分线相交于一点，这个交点称为三角形的外心.1、三角形的三边垂直平分线必交于一点已知：如图10，在△ABC 中，AB,AC 的垂直平分线DO,EO 相交于点O求证：O 点在BC 的垂直平分线上证明：连结AO,BO,CO ，∵DO 垂直平分AB ，∴AO=BO ∵EO 垂直平分AC ，∴AO=CO∴BO=CO 即O 点在BC 的垂直平分线上2、三角形外心的性质(1).三角形的外心到三个顶点的距离相等，都等于三角形的外接圆半径R ，即OA=OB=OC=R; (2).锐角三角形的外心在三角形内；钝角三角形的外心在三角形外；直角三角形的外心与斜边的中点重合;(3).∠BOC=2∠BAC ，∠AOB=2∠ACB ，∠COA=2∠CBA.例5：已知：△ABC 中，AB=AC=13，BC=10. 求：（1）△ABC 内切圆的半径r ； （2）△ABC 外接圆的半径R.例6：已知△ABC 的重心和内心为同点O ，求证：△ABC 为正三角形.图11 练习1.若想在一块质地均匀的三角形木板上穿一根线，使它水平地悬在空中，则穿线的位置应该是三角形木板的（ ）A. 垂心B. 重心C. 内心D. 外心2.如图11，D 是△ABC 的边BC 上的上点，点E 、F 分别是△ABD 和△ACD 的重心，连结EF 交AD 于点G ，则GADG___________.3.若三角形的垂心和重心重合，求证：该三角形为正三角形.4． （1） 若三角形ABC 的面积为S ，且三边长分别为a b c 、、，则三角形的内切圆的半径是___________;（2）若直角三角形的三边长分别为a b c 、、（其中c 为斜边长），则三角形的内切圆的半径是___________. 并请说明理由.5.求证：三角形的任一顶点到垂心的距离，等于外心到对边的距离的二倍．。

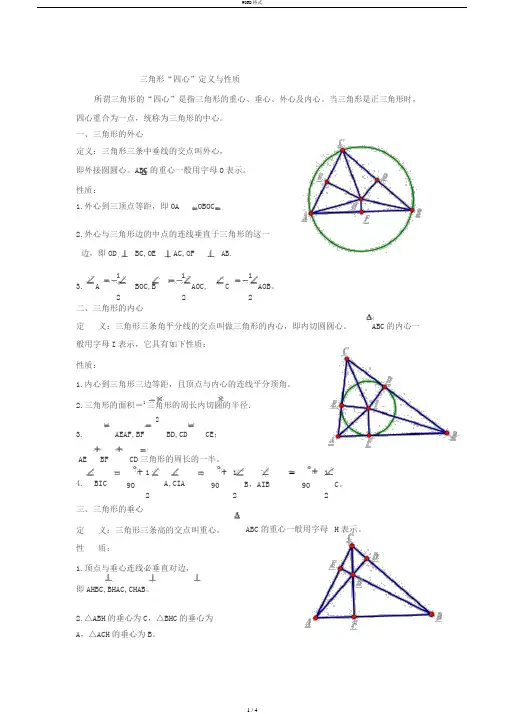
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC的重心一般用字母O表示。

性质：1.外心到三顶点等距，即OA OB OC。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即OD BC,OE AC,OF AB.3. A 1BOC,B1AOC,C1AOB。

2 2 2二、三角形的内心定义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC的内心一般用字母I表示，它具有如下性质：性质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝1三角形的周长内切圆的半径．23. AEAF,BF BD,CD CE；AE BF CD三角形的周长的一半。

4. BIC1A,CIA1B，AIB1C。

90 90 902 2 2三、三角形的垂心定义：三角形三条高的交点叫重心。

ABC的重心一般用字母H表示。

性质：1.顶点与垂心连线必垂直对边，即AHBC,BHAC,CH AB。

2.△ABH的垂心为C，△BHC的垂心为A，△ACH的垂心为B。

四、三角形的“重心”：定义：三角形三条中线的交点叫重心。

ABC 的重心一般用字母G 表示。

性质：1. 顶点与重心G 的连线必平分对边。

2. 重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GA2GD,GB2GE,GC2GF3.重心的坐标是三顶点坐标的平均值．即x G x A x B xC,y Gy A y B yC .334.向量性质：（1）GAGB GC0 ；（2）PG 1(PAPB PC)，31S5.S BGC SCGASAGBABC 。

3五、三角形“四心”的向量形式：结论1：若点O 为 ABC 所在的平面内一点，满足OAOB OBOC OCOA ，则点O 为 ABC 的垂心。

专题27 圆锥曲线与四心问题 微点3 圆锥曲线与内心问题专题27 圆锥曲线与四心问题 微点3 圆锥曲线与内心问题 【微点综述】三角形的“四心”指重心、外心、内心、垂心，它们是三角形的重要几何点，与之相关的数学问题是数学竞赛的热点问题，也是解析几何的难点问题，这类问题涉及的知识面较广，富有挑战性，是考查学生能力的“好”点，在高考中常充当“把关题”的重要角色．本文对三角形的“内心”的几何性质加以归纳，旨在探索解题规律，总结解题方法． 一、三角形内心的定义三角形的内心：三角形内切圆的圆心，称为内心，三角形三条内角平分线的交点，就是内心． 二、三角形内心常见结论设ABC 的内切圆为圆I ，切边AB 于P ，则有如下重要结论：（1）I 是ABC 的内心0a IA b IB c IC ⇔⋅+⋅+⋅= （其中a 、b 、c 为ABC 的三条边）； （2）1902BIC A ∠=︒+∠；（3）2tan2r b c aAP A +-==； （4）内心I 点的坐标为,A B C A B C ax bx cx ay by cy a b c a b c ++++⎛⎫⎪++++⎝⎭； （5）三角形内切圆的半径求法： ①任意三角形：2Sr C（其中C 为ABC 的周长，S 为ABC 的面积）； ①直角三角形：2a b cr +-=（其中a ，b 为直角边，c 为斜边）； （6）焦点三角形内心轨迹方程：①设点M 为椭圆()222210x y a b a b+=>>的焦点三角形12PF F 的内心，则点M 的轨迹方程为：()222210x y y c bc a c +=≠⎛⎫ ⎪+⎝⎭，其中22c a b -证明：如图1，设()()00,,,M x y P x y ，连结PM 交12F F 直线于点()1,0D x ，由三角形内角平分线定性质知12121212MP PF PF PF PF aMD F D F D F D F D c +====+，又20011112,,cx c x PF a F D x c x a a=+=+∴=．又由aMP MD c=，得()()222200002222,,1,10a c y x y axx y x y y c c a b c bc a c +==+=∴+=≠⎛⎫ ⎪+⎝⎭．图1 图2①设点I 为双曲线()222210,0x y a b a b-=>>的焦点三角形12PF F 的内心，则有：（1）当P 在双曲线右支上时，点I 的轨迹方程为(),0x a y b y =<≠； （2）当P 在双曲线左支上时，点I 的轨迹方程为(),0x a y b y =-<≠．证明：（1）当P 在双曲线右支上时，如图2，设圆I 与1212,,PF PF F F 分别相切于点,,A B C ，则有1122,,F A FC PA PB F B F C ===．①P 在双曲线右支上，122PF PF a ∴-=，即122F A F B a -=，又122FC F C a -=，设(),0C x '，则有()()2x c c x a ''----=，化简，有x a '=．从而知总圆I 与x 轴相切于点(),0C a ，又IC x ⊥轴，故点I 的轨迹方程为x a =．设I 的纵坐标为12,y PF F α∠=，则有1tan ,2ay c a c y b b c a b cα--=<=∴<+且0y ≠． 综上所述，点I 的轨迹为(),0x a yby =<≠．（2）仿照（1）的证明可证得：当P 在双曲线左支上时，圆I 总与x 轴相切于点(),0C a -，点I 的轨迹为(),0x a y b y =-<≠． 三、典型例题精析（一）内心的性质问题利用椭圆（双曲线）的焦点三角形的内心的基本性质，可以用来破解涉及内心的半径、线段的距离、夹角、离心率等相关的问题．破解的关键就是充分利用内心的基本性质，合理建立相应的关系式来分析与求解．1．已知M 是椭圆2212516x y +=上一点，1F ，2F 是椭圆的左，右焦点，点I 是12MF F ∆的内心，延长MI 交线段12F F 于N ，则MI IN的值为（ ）A ．53B ．35C ．43D ．342．已知双曲线2222:1x y C a b-=（0a >，0b >）的两条渐近线与抛物线22y px =（0p >）的准线分别交于A ，B 两点，O 为坐标原点，若双曲线C 的离心率为2，AOB 3则AOB 的内切圆半径为（ ） A 31B 31C ．233D ．333．已知椭圆()222210x y a b a b+=>>的左右焦点分别为1F ，2F ，P 为椭圆上不与左右顶点重合的任意一点，I 是12PF F △的内心，当4P I y y =时（其中P y ，I y 分别为点P 与内心I 的纵坐标），椭圆的离心率为（ ） A ．12B 3C ．13D 6 4．过双曲线2222:1(0,0)x y C a b a b -=>>的右焦点F 作直线l ，且直线l 与双曲线C 的一条渐近线垂直，垂足为A ，直线l 与另一条渐近线交于点B ，已知O 为坐标原点，若OAB ∆的内切圆31-，则双曲线C 的离心率为（ ） A 23B 31C 43D 232 5．已知12,F F 为双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点，过点1F 作一条渐近线的垂线交双曲线右支于点P ，直线2PF 与y 轴交于点Q （P ，Q 在x 轴同侧），连接1QF ，如图，若1PQF △内切圆圆心恰好落在以12F F 为直径的圆上，则12F PF ∠=________；双曲线的离心率e =________．二、内心的轨迹问题利用椭圆的焦点三角形的内心的基本性质，可以用来破解涉及内心的轨迹方程、参数的取值范围等相关的问题．破解的关键就是充分利用内心的基本性质，合理引人参数并能巧妙代换与应用．6．已知12,F F 为椭圆22:143x y C +=的左、右焦点，点P 在椭圆C 上移动时，12PF F ∆的内心I的轨迹方程为__________．7．点1F 、2F 分别是双曲线2213yx -=的左、右焦点，点P 在双曲线上，则12PF F ∆的内切圆半径r 的取值范围是A ．(B ．()0,2C ．(D ．()0,18．已知点P 为双曲线22221(0,0)x y a b a b-=>>右支上一点，点F 1，F 2分别为双曲线的左右焦点，点I 是①PF 1F 2的内心（三角形内切圆的圆心），若恒有121222IPF IPF IF F S SS -≥成立，则双曲线的离心率取值范围是（ ）A ．（1B ．（1，）C ．（1，D ．（1]三、内心的应用问题利用椭圆（双曲线）的焦点三角形的内心的基本性质，可以用来破解涉及内心的一些基本应用问题，包括直线的斜率、三角形的面积等相关问题．破解的关键就是充分利用内心的基本性质，交汇直线的基本概念、三角形的基本元素等，综合起来破解相应的综合应用问题．9．已知点P 是双曲线22221x y a b-=上除顶点外的任意一点，12,F F 分别为左、右焦点，c 为半焦距，12PF F ∠的内切圆与12F F 切于点M ，则12FM F M ⋅=_________. 10．已知双曲线22:13y M x -=的左，右焦点F 1，F 2，点P 在双曲线上左支上动点，则三角形PF1F2的内切圆的圆心为G ，若1GPF △与12GF F △的面积分别为,'S S ，则'SS 取值范围是____________11．已知F 1，F 2分别为双曲线22221(0,0)x y a b a b-=>>的左焦点和右焦点，过F 2的直线l 与双曲线的右支交于A ，B 两点，△AF 1F 2的内切圆半径为r 1，△BF 1F 2的内切圆半径为r 2，若r 1=2r 2，则直线l 的斜率为（ ） A ．1 B 2 C ．2D ．2小结：涉及椭圆的焦点三角形的内心问题，可以通过多种形式加以变化与应用，多姿多彩，创新新颖，极富美感．破解涉及焦点三角形的内心问题的关键就是充分利用焦点三角形的内心的基本性质，有效利用解析几何、平面几何、三角函数等相关知识加以综合，值得我们不断深人学习，探究分析，拓展思维，提升应用，从而不断开拓学生的解题境界，提升学生的解题能力，养成良好的数学品质，培养数学核心素养． 【强化训练】12．椭圆()222210x y a b a b+=>>的两焦点是1F 、2F ，M 为椭圆上与1F 、2F 不共线的任意一点，I 为12MF F △的内心，延长MI 交线段12F F 于点N ，则:MI IN 的值等于（ ）A ．abB ．a cC ．bcD ．c a13．如图所示，点P 为椭圆22143x y +=上任一点，1F ，2F 为其左右两焦点，12PF F △的内心为I ，则1212IF F PFF S S=（ ）A ．13B ．12C ．23D ．3414．已知椭圆C ：22221(0)x y a b a b+=>>，12,F F 为左右焦点，点P 在椭圆C 上，12F PF △的重心为G ，内心为I ，且有12IG F F λ=（λ为实数），则椭圆方程为( )A ．22186x y +B ．221164x y +=C ．2251927x y +=D ．221105x y += 15．已知点M 在椭圆：()222210x y a b a b+=>>上，1F 、2F 为左、右焦点，点T 是12MF F ∆内心，连接MT 并延长交线段12F F 于N ，则MT TN的值为AB C D 16．双曲线22122:1(0,0)x y C a b a b-=>>的渐近线与抛物线22:2(0)C x py p =>交于点,,A O B ，若抛物线2C 的焦点恰为AOB ∆的内心，则双曲线1C 的离心率为（ ）A ．32B C D 12217．双曲线221916x y -=的左、右焦点分别为1F ，2F ，P 为双曲线右支上一点，I 是12PF F ∆的内心，且2112IPF IPF IF F S S S λ∆∆∆=-，则λ=（ ） A ．35 B ．45-C ．35D ．4518．点A 是椭圆()222210x y a b a b+=>>上一点，12,F F 分别是椭圆的左右焦点，I 是12AF F △的内心．若112222IAF IF F IAF SSS=-，则该椭圆的离心率为（ ）A ．14B C ．12D ．219．设椭圆2214x y +=的左、右焦点分别为12,F F ，M 是椭圆上异于长轴端点的一点，212F MF θ=∠，12MF F △的内心为I ，则||cos MI θ=（ ）A ．2B ．12C D 20．已知12,F F 分别是椭圆()2222:10x ya b a bΓ+=>>的左、右焦点，点P 是椭圆上一点，I 为12PF F ∆的内心，若12124PF F IF F S S ∆∆=，则该椭圆的离心率是（ ）A ．13B ．14C 2D 2 21．已知椭圆2222:1(0)x y C a b a b +=>>的左､右焦点分别为1F ，2F ，P 为C 上一点，若I 为12PF F △的内心，且12123PF F IF F S S =△△，则C 的方程可能是A ．2212x y +=B ．2213x y +=C ．22132x y +=D ．22143x y +=22．已知()11,0F -，21,0F ，M 是第一象限内的点，且满足124MF MF +=，若I 是12MF F △的内心，G 是12MF F △的重心，记12IF F △与1GF M △的面积分别为1S ，2S ，则（ ） A ．12S S >B ．12S SC ．12S S <D ．1S 与2S 大小不确定23．设F 是双曲线222:1(0,0)x y C a b a b-=>>的右焦点，O 为坐标原点，过F 作C 的一条渐近线的垂线，垂足为H ，若FOH 的内切圆与x 轴切于点B ，且2BF OB =，则C 的离心率为（ ） A 317+ B 417+C 3317+ D 3317+24．已知双曲线22221x y a b -=的左右焦点为12,,F F O 为它的中心，P 为双曲线右支上的一点，12PF F ∆的内切圆圆心为I ，且圆I 与x 轴相切于A 点，过2F 作直线PI 的垂线，垂足为B ，若双曲线的离心率为e ，则 A ．||||OB OA = B ．||||OB e OA = C ．||||OA e OB = D ．||OB 与||OA 关系不确定25．点P 是双曲线22:1916y x C -=的上支上的一点，F 1，F 2分别为双曲线的上、下焦点，则△PF 1F 2的内切圆圆心M 的坐标一定适合的方程是（ ） A ．y=-3B ．y=3C ．x 2+y 2=5D ．y=3x 2-226．已知点P 为双曲线()222210,0x y a b a b -=>>右支上一点，12,F F 分别为双曲线的左右焦点，且212,b F F I a=为三角形12PF F 的内心，若1212IPF IPF IF F S S S λ∆∆∆=+成立，则λ的值为A 122+B ．231 C 21 D 2127．如图，已知双曲线22221x y a b-=（0a >，0b >）的左右焦点分别为F 1、F 2，128F F =，P是双曲线右支上的一点，直线2PF 与y 轴交于点A ，1APF △的内切圆在边1PF 上的切点为Q ，若2PQ =，则该双曲线的离心率为（ ）AB C ．2D ．328．已知点P 为双曲线:C 22221(00)x y a b a b－，=>>右支上一点，12,F F 分别为左右焦点，若双曲线C 12PF F ∆的内切圆圆心为I ，半径为2，若12PF I PF I S S ∆∆=+则b 的值是A ．2BC D ．629．点P 是双曲线22221x y a b -=右支上一点，12F F 、分别为左、右焦点.12PF F ∆的内切圆与x 轴相切于点N .若点N 为线段2OF 中点，则双曲线离心率为（ ）A 1B ．2C D ．330．如图，已知椭圆22221(0)x y a b a b+=>>的左，右焦点分别为12,F F ，12F F =，P 是y 轴正半轴上一点，1PF 交椭圆于A ，若21AF PF ⊥，且2APF ∆2心率为A B C D31．过双曲线()222210x y a b a b-=>>右焦点F 的直线交两渐近线于A 、B 两点，若0OA AB ⋅=，O 为坐标原点，且OAB 31-，则该双曲线的离心率为 A 23B 3C 43D 3132．已知椭圆22122:1(0)x y C a b a b +=>>的左、右焦点分别是,M N ，过点M 作圆222:O x y b +=的一条切线，切点为P ，延长MP 交椭圆于点Q ，且||||MP PQ =，双曲线22222:1x y C a b-=的左、右焦点分别为12,,F F E 是2C 右支上一点，1EF 与y 轴交于点A ，2EAF 的内切圆与2AF 的切点为F ，若||3AF =2C 的方程为A ．22134x y -=B ．22143x y -=C ．22193x y -=D ．223134x y -=33．设1F ，2F 为双曲线22221(0,0)x y a b a b-=>>的左、右焦点，点()0,2P x a 为双曲线上一点，若12PF F ∆的重心和内心的连线与x 轴垂直，则双曲线的离心率为 A 6B 5C 6D 534．已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点为1F ，2F ，P 为双曲线C 右支上异于顶点的一点，12PF F △的内切圆与x 轴切于点(1,0)，且P 与点1F 关于直线bxy a=-对称，则双曲线方程为_________．35．点M 为椭圆22195x y +=上一点，12,F F 为椭圆的两个焦点，则12F MF △的内心轨迹方程为____________.36．设12,F F 为椭圆C :2214x y +=的两个焦点．M 为C 上点，12MF F ∆的内心I 的纵坐标为2312F MF ∠的余弦值为_____。

平面向量痛点问题之三角形“四心”问题【题型归纳目录】题型一：重心定理题型二：内心定理题型三：外心定理题型四：垂心定理【知识点梳理】一、四心的概念介绍：(1)重心：中线的交点，重心将中线长度分成2：1．(2)内心：角平分线的交点(内切圆的圆心)，角平分线上的任意点到角两边的距离相等．(3)外心：中垂线的交点(外接圆的圆心)，外心到三角形各顶点的距离相等．(4)垂心：高线的交点，高线与对应边垂直．二、三角形四心与推论：(1)O 是△ABC 的重心：S △BOC :S △COA :S △A 0B =1:1:1⇔OA +OB +OC =0．(2)O 是△ABC 的内心：S △B 0C :S △COA :S △AOB =a :b :c ⇔aOA +bOB +cOC =0．(3)O 是△ABC 的外心：S △B 0C :S △COA :S △AOB =sin2A :sin2B :sin2C ⇔sin2AOA +sin2BOB +sin2COC =0 ．(4)O 是△ABC 的垂心：S △B 0C :S △COA :S △AOB =tan A :tan B :tan C ⇔tan AOA +tan BOB +tan COC =0．【方法技巧与总结】(1)内心：三角形的内心在向量AB AB +ACAC所在的直线上.AB ⋅PC +BC ⋅PC +CA⋅PB =0 ⇔P 为△ABC 的内心.(2)外心：PA =PB =PC⇔P 为△ABC 的外心.(3)垂心：PA ⋅PB =PB ⋅PC =PC ⋅PA⇔P 为△ABC 的垂心.(4)重心：PA +PB +PC =0⇔P 为△ABC 的重心.【典型例题】题型一：重心定理1(2024·重庆北碚·高一西南大学附中校考阶段练习)如图所示，已知点G 是△ABC 的重心，过点G 作直线分别与AB ，AC 两边交于M ，N 两点(点N 与点C 不重合)，设AM =xAB ,AN =yAC ，则1x +1y的值为()A.3B.4C.5D.62(2024·全国·高一随堂练习)已知△ABC 中，点G 为△ABC 所在平面内一点，则“AB +AC -3AG=0”是“点G 为△ABC 重心”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3(2024·全国·高一专题练习)已知O 是三角形ABC 所在平面内一定点，动点P 满足OP =OA+λAB AB sin B +AC AC sin C λ≥0 ，则P 点轨迹一定通过三角形ABC 的()A.内心B.外心C.垂心D.重心题型二：内心定理1(2024·全国·高一专题练习)在△ABC 中，cos ∠BAC =13，若O 为内心，且满足AO =xAB +yAC ，则x +y 的最大值为．2(2024·江苏南通·高一如皋市第一中学期末)已知点P 为△ABC 的内心，∠BAC =23π,AB =1,AC =2，若AP =λAB +μAC，则λ+μ=．3(2024·广西柳州·高一统考期末)设O 为△ABC 的内心，AB =AC =5，BC =8，AO =mAB+nBCm ,n ∈R ，则m +n =题型三：外心定理1(2024·吉林长春·高一东北师大附中校考阶段练习)已知点O 是△ABC 的外心，AB =4，AC =2，∠BAC 为钝角，M 是边BC 的中点，则AM ⋅AO=．2(2024·安徽六安·高一六安市裕安区新安中学校考期末)已知O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足OP =OA +OB 2+λCA CA cos A +CBCB cos B ，λ∈R ，则P 的轨迹一定经过△ABC 的．(从“重心”，“外心”，“内心”，“垂心”中选择一个填写)3(2024·四川遂宁·高一射洪中学校考阶段练习)已知△ABC 中，∠A =60°，AB =6，AC =4，O 为△ABC 的外心，若AO =λAB +μAC，则λ+μ的值为()A.1B.2C.1118D.12题型四：垂心定理1(2024·江苏泰州·高一统考期末)已知△ABC 的垂心为点D ，面积为15，且∠ABC =45°，则BD ⋅BC=；若BD =12BA +13BC ，则BD=.2(2024·湖北黄冈·高一校联考期末)若O 为△ABC 的垂心，2OA +3OB +5OC =0 ，则S △AOB S △AOC=，cos ∠BOC =．3(2024·山西·高一校联考阶段练习)已知H 为△ABC 的垂心(三角形的三条高线的交点)，若AH=13AB+25AC ，则sin ∠BAC =.【过关测试】一、单选题1(2024·全国·高一专题练习)在直角三角形ABC 中，A =90°，△ABC 的重心、外心、垂心、内心分别为G 1，G 2，G 3，G 4，若AG i =λi AB +μi AC(其中i =1,2,3,4)，当λi +μi 取最大值时，i =()A.1B.2C.3D.42(2024·黑龙江牡丹江·高一牡丹江一中校考阶段练习)若O 是△ABC 所在平面上一定点，H ，N ，Q 在△ABC 所在平面内，动点P 满足OP =OA +λAB AB +ACAC，λ∈0,+∞ ，则直线AP 一定经过△ABC 的心，点H 满足HA = HB = HC ，则H 是△ABC 的心，点N 满足NA +NB +NC=0，则N 是△ABC 的心，点Q 满足QA ·QB =QB ·QC =QC ·QA ，则Q 是△ABC 的心，下列选项正确的是()A.外心，内心，重心，垂心B.内心，外心，重心，垂心C.内心，外心，垂心，重心D.外心，重心，垂心，内心二、多选题3(2024·河南郑州·高一校联考期末)点O 为△ABC 所在平面内一点，则()A.若OA +OB +OC =0 ，则点O 为△ABC 的重心B.若OA ⋅AC AC -AB AB =OB ⋅BC BC -BABA =0，则点O 为△ABC 的垂心C.若OA +OB ⋅AB =OB +OC ⋅BC=0．则点O 为△ABC 的垂心D.在△ABC 中，设AC 2 -AB 2 =2AO ⋅BC，那么动点O 的轨迹必通过△ABC 的外心4(2024·内蒙古呼和浩特·高一呼市二中校考阶段练习)设点M 是△ABC 所在平面内一点，则下列说法正确的是()A.若AM =12AB +12AC ，则点M 是边BC 的中点B.若AM =2AB -AC ，则点M 是边BC 的三等分点C.若AM =-BM -CM ，则点M 是边△ABC 的重心D.若AM =xAB +yAC ，且x +y =13，则△MBC 的面积是△ABC 面积的235(2024·山东枣庄·高一校考阶段练习)数学家欧拉在1765年发表的《三角形的几何学》一书中提出定理：三角形的外心、重心、垂心依次位于同一条直线上，且重心到外心的距离是重心到垂心距离的一半，此直线被称为三角形的欧拉线，该定理则被称为欧拉线定理.设点O 、G 、H 分别是△ABC 的外心、重心、垂心，且M 为BC 的中点，则()A.OH =OA +OB +OCB.S △ABG =S △BCG =S △ACGC.AH =3OMD.AB +AC =4OM +2HM6(2024·安徽池州·高一统考期末)已知△ABC 的重心为O ，边AB ,BC ,CA 的中点分别为D ,E ,F ，则下列说法正确的是()A.OA +OB =2ODB.若△ABC 为正三角形，则OA ⋅OB +OB ⋅OC +OC ⋅OA=0C.若AO ⋅AB -AC=0，则OA ⊥BC D.OD +OE +OF =07(2024·广东广州·高一校考期末)下列命题正确的是()A.若A ，B ，C ，D 四点在同一条直线上，且AB =CD ，则AB =CDB.在△ABC 中，若O 点满足OA +OB +OC =0，则O 点是△ABC 的重心C.若a =(1,1)，把a 右平移2个单位，得到的向量的坐标为(3,1)D.在△ABC 中，若CP =λCA |CA |+CB|CB |，则P 点的轨迹经过△ABC 的内心8(2024·新疆·高一兵团第三师第一中学校考阶段练习)点O 在△ABC 所在的平面内，则下列结论正确的是()A.若OA ⋅OB =OB ⋅OC =OC ⋅OA ，则点O 为△ABC 的垂心B.若OA +OB +OC =0 ，则点O 为△ABC 的外心C.若2OA +OB +3OC =0，则S △AOB :S △BOC :S △AOC =3:2:1D.若AO ⋅AB AB =AO ⋅AC AC 且CO ⋅CA CA =CO ⋅CB CB ，则点O 是△ABC 的内心三、填空题9(2024·甘肃武威·高一校联考期末)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ，若O 为△ABC 的重心，OB ⊥OC ,3b =4c ，则cos A =.10(2024·全国·高一专题练习)点O 是平面上一定点，A 、B 、C 是平面上△ABC 的三个顶点，∠B 、∠C 分别是边AC 、AB 的对角，以下命题正确的是(把你认为正确的序号全部写上)．①动点P 满足OP =OA +PB +PC，则△ABC 的重心一定在满足条件的P 点集合中；②动点P 满足OP =OA +λAB |AB |+AC|AC |(λ>0)，则△ABC 的内心一定在满足条件的P 点集合中；③动点P 满足OP =OA +λAB |AB |sin B +AC|AC|sin C(λ>0)，则△ABC 的重心一定在满足条件的P 点集合中；④动点P 满足OP =OA+λAB |AB |cos B +AC|AC|cos C(λ>0)，则△ABC 的垂心一定在满足条件的P 点集合中；⑤动点P 满足OP =OB +OC 2+λAB |AB |cos B +AC|AC|cos C(λ>0)，则△ABC 的外心一定在满足条件的P 点集合中．11(2024·辽宁·高一校联考期末)某同学在学习和探索三角形相关知识时，发现了一个有趣的性质：将锐角三角形三条边所对的外接圆的三条圆弧(劣弧)沿着三角形的边进行翻折，则三条圆弧交于该三角形内部一点，且此交点为该三角形的垂心(即三角形三条高线的交点).如图，已知锐角△ABC 外接圆的半径为2，且三条圆弧沿△ABC 三边翻折后交于点P .若AB =3，则sin ∠PAC =；若AC :AB :BC =6:5:4，则PA +PB +PC 的值为.12(2024·宁夏银川·高一银川唐徕回民中学校考期末)已知P 为△ABC 所在平面内一点，有下列结论：①若P 为△ABC 的内心，则存在实数λ使AP =λAB |AB |+AC|AC |；②若PA +PB +PC =0 ，则P 为△ABC 的外心；③若PA =PB =PC ，则P 为△ABC 的内心；④若AP =13AB +23AC ，则△ABC 与△ABP 的面积比为2:3．其中正确的结论是．(写出所有正确结论的序号)13(2024·广西河池·高一校联考阶段练习)在△ABC 中，已知AB =5，AC =3，A =2π3，I 为△ABC 的内心，CI 的延长线交AB 于点D ，则△ABC 的外接圆的面积为，CD =.14(2024·四川遂宁·高一遂宁中学校考阶段练习)已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP =OB +OC 2+λAB AB cos B +ACAC cos C ，λ∈0,+∞ ，则动点P 的轨迹一定通过△ABC 的(填序号)．①内心 ②垂心 ③ 重心 ④外心15(2024·高一课时练习)已知O 为△ABC 的内心，∠BAC =π3，且满足AO =xAB +yAC ，则x +y 的最大值为．16(2024·高一课时练习)已知A ，B ，C 是平面内不共线的三点，O 为ΔABC 所在平面内一点，D 是AB 的中点，动点P 满足OP =132-2λ OD +1+2λ OCλ∈R ，则点P 的轨迹一定过△ABC 的(填“内心”“外心”“垂心”或“重心”).17(2024·高一课时练习)已知点O 是ΔABC 的内心，若AO =37AB +17AC，则cos ∠BAC =.18(2024·四川成都·高一成都市锦江区嘉祥外国语高级中学校考阶段练习)已知点O 是△ABC 的外心，AB =6，BC =8，B =2π3，若BO =xBA +yBC ，则3x +4y =．19(2024·湖北武汉·高一期末)△ABC 中，AB =2，BC =26，AC =4，点O 为△ABC 的外心，若AO=mAB +nAC ，则实数m =．20(2024·湖北·高一校联考阶段练习)在△ABC 中，已知AB =2,AC =5,∠BAC =60°，P 是△ABC 的外心，则∠APB 的余弦值为.21(2024·四川达州·高一达州中学校考阶段练习)设O 为△ABC 的外心a ，b ，c 分别为角A ，B ，C 的对边，若b =3，c =5，则OA ⋅BC=．22(2024·广东汕头·高一金山中学校考期末)已知O 为△ABC 的外心，若AO ⋅BC =4BO ⋅AC ，则cos A 最小值.23(2024·重庆渝中·高一重庆巴蜀中学校考期末)某同学在查阅资料时，发现一个结论：已知O 是△ABC 内的一点，且存在x ,y ,z ∈R ，使得xOA +yOB +zOC =0，则S △AOB :S △AOC :S △COB =z :y :x ．请以此结论回答：已知在△ABC 中，∠A =π4，∠B =π3，O 是△ABC 的外心，且AO =λAB +μAC λ,μ∈R ，则λ+μ=．24(2024·辽宁大连·高一育明高中校考期末)已知点P 在△ABC 所在的平面内，则下列各结论正确的有①若P 为△ABC 的垂心，AB ⋅AC =2，则AP ⋅AB =2②若△ABC 为边长为2的正三角形，则PA ⋅PB +PC的最小值为-1③若△ABC 为锐角三角形且外心为P ，AP =xAB +yAC且x +2y =1，则AB =BC④若AP =1AB cos B +12 AB +1ACcos C+12AC ，则动点P 的轨迹经过△ABC 的外心25(2024·全国·高一专题练习)(1)已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个动点，若动点P 满足OP =OA +λ(AB +AC)，λ∈(0,+∞)，则点P 的轨迹一定通过△ABC 的(填“内心”“外心”“重心”或“垂心” )．(2)已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个动点，若动点P 满足OP =OA +λAB |AB |+AC |AC |，λ∈(0,+∞)，则点P 的轨迹一定通过△ABC 的．(填“内心”“外心”“重心”或“垂心” )四、解答题26(2024·全国·高一专题练习)已知△ABC 中，过重心G 的直线交边AB 于P ，交边AC 于Q ，设△APQ 的面积为S 1，△ABC 的面积为S 2，AP =pPB ，AQ =qQC.(1)求GA +GB +GC ；(2)求证：1p +1q =1.(3)求S1S 2的取值范围.。

三角形“四心”定义与性质-CAL-FENGHAI.-(YICAI)-Company One1三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定 义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性 质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。

二、三角形的内心 定 义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示，它具有如下性质：性 质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3.CE CD BD BF AF AE ===,,；=++CD BF AE 三角形的周长的一半。

4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ，C AIB ∠+=∠2190 。

三、三角形的垂心定 义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性 质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B 。

四、三角形的“重心”：定 义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性 质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值． 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质：（1）0=++GC GB GA ；（2）)(31++=，5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。

第二十八讲 三角形的四心一、三角形的外心1．定义：三角形三边中垂线的交点（即外接圆的圆心）。

2．性质与判定：⑴ 点O 为△ABC 的外心OA OB OC ⇔==；⑵ 点O 为△ABC 的外心且90A ∠≤,2OB OC BOC A ⇔=∠=∠；⑶ 点O 为△ABC 的外心且90A ∠>,3602OB OC BOC A ⇔=∠=-∠。

二、三角形的重心1．定义：三角形三边中线的交点。

2．性质与判定：⑴ 点G 为△ABC 的重心⇔点G 分任一条中线之比为2:1；⑵ 点G 为△ABC 的重心⇔S △GBC = S △GAB = S △GCA =13S △ABC 。

三、三角形的内心1．定义：三角形三条角平分线的交点（即内切圆的圆心）。

2．性质与判定：点I 为△ABC 的内心⇔点I 到三边的距离相等且点I 在三角形内部；3．三角形面积与内切圆半径及三边关系：1()2S a b c r =++⋅。

四、三角形的垂心定义：三角形三高的交点。

五、四心间的关系三角形的四心之间有十分密切的关系，其中最典型的是欧拉线，三角形的垂心H 、重心G 以及外心三点共线且HG=2OG ；欧拉公式：22222,4OI R Rr OH R Rr =-=-； 对于正三角形来说，四心重合，这个点也叫做三角形的中心；对于锐角三角形来说，设点P 为△ABC 内一点，且P 点到BC 、CA 、AB 的距离分别为x,y,z ，则：⑴ 若P 为内心：::1:1:1x y z =⑵ 若P 为重心：111::::x y z a b c= ⑶ 若P 为外心：::cos :cos :cos x y z A B C =⑷ 若P 为垂心：111::::cos cos cos x y z A B C=【例1】如图，已知平行四边形ABCD 中，点E 是AB 的中点，AB=10，AC=9，DE=12。

求平行四边形ABCD 的面积。

思路点拨：设AC 交DE 于O ，可推出G 为△ABD 重心。

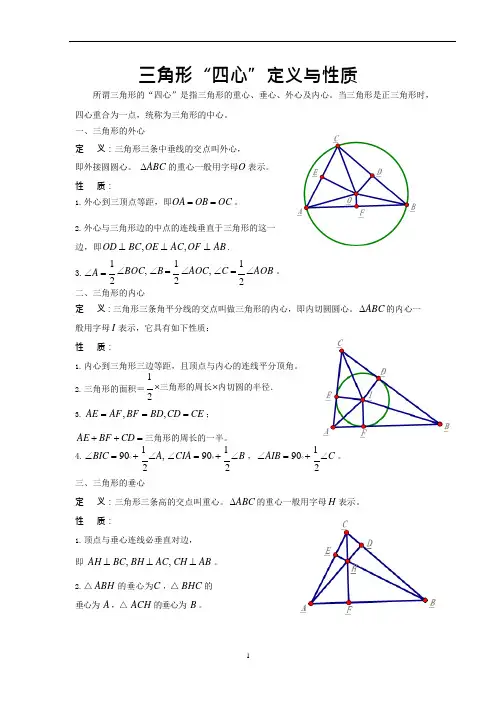
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定义：三角形三条中垂线的交点叫外心，即外接圆圆心。

∆ABC 的重心一般用字母O 表示。

性质：1.外心到三顶点等距，即OA =OB =OC 。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即OD ⊥BC, OE ⊥AC, OF ⊥AB .3. ∠A = 1∠BOC, ∠B =21∠AOC, ∠C =21∠AOB 。

2二、三角形的内心定义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

∆ABC 的内心一般用字母I 表示，它具有如下性质：性质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

12.三角形的面积＝⨯三角形的周长⨯内切圆的半径．23.AE =AF ,BF =BD, C D =CE ；AE +BF +CD =三角形的周长的一半。

4. ∠BIC = 90 +1∠A, ∠CIA = 90 +1∠B ，∠AIB = 90 +1∠C 。

2 2 2三、三角形的垂心定义：三角形三条高的交点叫重心。

∆ABC 的重心一般用字母H 表示。

性质：1.顶点与垂心连线必垂直对边，即AH ⊥BC, BH ⊥AC, CH ⊥AB 。

2.△ABH 的垂心为C ，△ BHC 的垂心为A ，△ ACH 的垂心为B 。

+ = + = + 四、三角形的“重心”：定义：三角形三条中线的交点叫重心。

∆ABC 的重心一般用字母G 表示。

性 质：1. 顶点与重心G 的连线必平分对边。

2. 重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2 倍。

即GA = 2GD , GB = 2GE , GC = 2GF3. 重心的坐标是三顶点坐标的平均值． 即 x G =x A + x B + x C , y 3 G = y A + y B + y C . 34. 向量性质：（1） GA + GB + GC = 0 ；1 （2） = (PA + PB + PC ) ，5. 3 S ∆BGC = S ∆CGA = S ∆AGB = 1 S 3∆ABC 。