平面几何三角形四心竞赛题A卷及答案

平面向量“四心”知识点总结与经典习题【强烈推荐】平面向量的“四心”是指三角形的外心、内心、重心和垂心，它们各自具有特殊的性质。

在高中数学中，向量问题经常与“四心”问题结合考查。

因此，熟悉向量的代数运算和几何意义是解决这类问题的关键。

四心知识点总结如下：重心：1.重心是三角形三条中线的交点，也是重心到三角形三个顶点距离之和最小的点。

2.重心坐标为$(\frac{1}{3}(x_A+x_B+x_C),\frac{1}{3}(y_A+y_B+y_C))$。

垂心：1.垂心是三角形三条高线的交点，也是垂足到三角形三边距离之积最大的点。

2.若垂心为$O$，则有$OA\cdot OB=OA\cdot OC=OB\cdot OC$。

外心：1.外心是三角形三条中垂线的交点，也是到三角形三个顶点距离相等的点。

2.若外心为$O$，则有$OA=OB=OC$，或$(OA+OB)\cdot AB=(OB+OC)\cdot BC=(OC+OA)\cdot CA$。

内心：1.内心是三角形三条角平分线的交点，也是到三角形三边距离之和最小的点。

2.若内心为$O$，则有$a\cdot OA+b\cdot OB+c\cdotOC=0$，其中$a,b,c$为三角形三边的长度。

下面是一些经典题：1.在$\triangle ABC$中，$D,E,F$分别为$BC,CA,AB$的中点，$M$为重心，则$\vec{AM}$等于（）。

A。

$\frac{1}{3}(\vec{AD}+\vec{BE}+\vec{CF})$B。

$\frac{1}{2}(\vec{AD}+\vec{BE}+\vec{CF})$C。

$\frac{1}{3}(\vec{AD}+\vec{BE}+\vec{CF})+\vec{OG}$ D。

$\frac{1}{2}(\vec{AD}+\vec{BE}+\vec{CF})+\vec{OG}$ 答案：C2.在$\triangle ABC$中，$O$为坐标原点，$P$满足$\vec{OP}=\frac{1}{3}(\vec{OA}+\vec{OB}+\vec{OC})$，则$P$一定在（）上。

三角形的四心习题及解析一、单选题1. ( )△ ABC 中，若/ A :/ B :/ C = 1 : 2: 3, G 为厶 ABC 的重心，则△ GAB 面积：△ GBC 面积：△ GAC 面 积=(A ) 1: 2:,3( B ) 1 :3 : 2( C )2: 1 : 3 ( D ) 1 : 1: 1。

答案：(D )/■△ GAB 面积：△ GBC 面积：△ GAC 面积=1: 1: 1答案：(C ) 答案：(B )2 22.()如图，△ ABC 中，AB = AC ，两腰上的中线相交与G ,若/ BGC = 90°22， 贝 U BE 的长为多少？ ( A ) 2( B )2^2( C ) 3 ( D )4。

，且BC解析：T AB = AC ，且 GABC 的重心 A BE = CD ■- BG = CG BC 2：2--BG = — == 2*2v'2ABE = 3BG =-皂=32 2又 T / BGC = 90 ° ，BC = 2.23.()如图，等腰△ ABC中，AB = AC = 13，BD = CD = 5，O ABC 的外心,?( A ) 117( B )24119( C ) 121( D ) 123。

242424 G 为△ ABC 的重心解析ABC为等腰三角形，二A D丄BCAD = '•. 132—52=12，连接 OB，令 OD = x ,贝UOB =OA = AD-0D= 12(12 — x) 2= x 2 + 52 x =119故选(B ) 244. ()如图，D 、E 分別为AB 、AC 中点，BE 、CD 交于F,若斜线部分的面积为7，则△ ACD 的面积为多少？( A ) 21( B ) 24( C ) 28( D ) 35。

答案：(A)5. ()直角三角形 ABC 中，/ A = 90°, O 为外心，G 为重心，若AC= 6, AB = 8,则2 4 5 7 OG=?(A)-(B )(C ) -(D )。

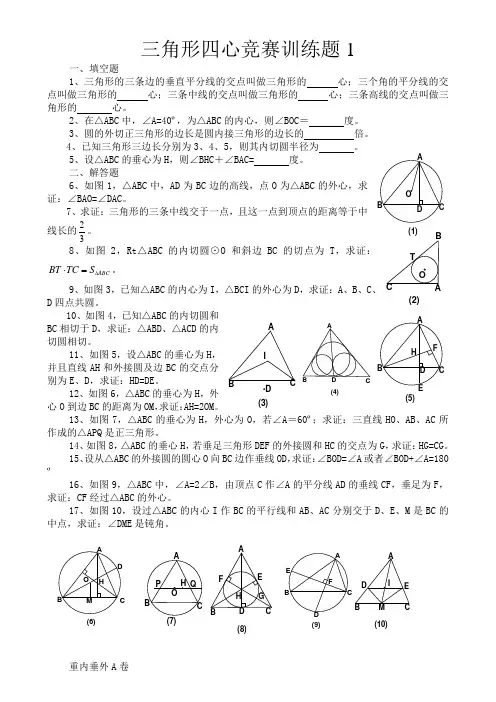
三角形四心竞赛训练题1一、填空题1、三角形的三条边的垂直平分线的交点叫做三角形的 心；三个角的平分线的交点叫做三角形的 心；三条中线的交点叫做三角形的 心；三条高线的交点叫做三角形的 心。

2、在△ABC 中，∠A=40º，为△ABC 的内心，则∠BOC ＝ 度。

3、圆的外切正三角形的边长是圆内接三角形的边长的 倍。

4、已知三角形三边长分别为3、4、5，则其内切圆半径为 。

5、设△ABC 的垂心为H ，则∠BHC ＋∠BAC= 度。

二、解答题6、如图1，△ABC 中，AD 为BC 边的高线，点O 为△ABC 的外心，求证：∠BAO=∠DAC 。

7、求证：三角形的三条中线交于一点，且这一点到顶点的距离等于中线长的23。

8、如图2，Rt △ABC 的内切圆⊙O 和斜边BC 的切点为T ，求证：ABCBT TC S ∆⋅=。

9、如图3，已知△ABC 的内心为I ，△BCI 的外心为D ，求证：A 、B 、C 、D 四点共圆。

10、如图4，已知△ABC 的内切圆和BC 相切于D ，求证：△ABD 、△ACD 的内切圆相切。

11、如图5，设△ABC 的垂心为H ，并且直线AH 和外接圆及边BC 的交点分别为E 、D ，求证：HD=DE 。

12、如图6，△ABC 的垂心为H ，外心O 到边BC 的距离为OM ，求证：AH=2OM 。

13、如图7，△ABC 的垂心为H ，外心为O ，若∠A ＝60º；求证：三直线HO 、AB 、AC 所作成的△APQ 是正三角形。

14、如图8，△ABC 的垂心H ，若垂足三角形DEF 的外接圆和HC 的交点为G ，求证：HG=CG 。

15、设从△ABC 的外接圆的圆心O 向BC 边作垂线OD ，求证：∠BOD=∠A 或者∠BOD+∠A=180º16、如图9，△ABC 中，∠A=2∠B ，由顶点C 作∠A 的平分线AD 的垂线CF ，垂足为F ，求证：CF 经过△ABC 的外心。

初中数学竞赛专项训练之三角形的四心及性质、平移、旋转、覆盖一、填空题：1、G 是△A BC 的重心，连结AG 并延长交边BC 于D ，若△ABC 的面积为6cm 2， 则△BGD 的面积为（ ）A. 2cm 2B. 3 cm 2C. 1 cm 2D. 23 cm 22、如图10-1，在Rt △ABC 中，∠C ＝90°，∠A ＝30°，∠C 的平分线与∠B 的外角的平分线交于E 点，则∠AEB 是（ ） A. 50° B. 45° C. 40° D. 35°3、在△ABC 中，∠ACB ＝90°，∠A ＝20°，如图10-2，将△ABC 绕点C 按逆时针方向旋转角α到∠A ’C ’B ’的位置，其中A ’、B ’分别是A 、B 的对应点，B 在A ’B ’上，CA ’交AB 于D ，则∠BDC 的度数为（ ） A. 40° B. 45° C. 50° D. 60°4、设G 是△ABC 的垂心，且AG ＝6，BG ＝8，CG ＝10，则三角形的面积为（ ） A. 58 B. 66 C. 72 D. 845、如图10-3，有一块矩形纸片AB CD ，AB ＝8，AD ＝6，将纸片折叠，使AD 边落在AB 边上，折痕为AE ，再将△AED 沿DE 向右翻折，AE 与BC 的交点为F ，△CEF 的面积为（ ） A. 2 B. 4 C. 6 D. 86、在△ABC 中，∠A ＝45°，BC ＝a ，高BE 、CF 交于点H ，则AH ＝（ ）A.a 21 B. a 22C. aD. a 2 7、已知点I 是锐角三角形ABC 的内心，A 1、B 1、C 1分别是点I 关于BC 、CA 、AB 的对称点，若点B 在△A 1B 1C 1的外接圆上，则∠ABC 等于（ ） A. 30° B. 45° C. 60° D. 90°8、已知AD 、BE 、CF 是锐角△ABC 三条高线，垂心为H ，则其图中直角三角形的个数是（ ） A. 6 B. 8 C. 10 D. 12二、填空题1、如图10-4，I 是△ABC 的内心，∠A ＝40°，则∠CIB ＝＿＿2、在凸四边形ABCD 中，已知AB ∶BC ∶CD ∶DA ＝2∶2∶3∶1，且∠ABC ＝90°，则∠DAB 的度数是＿＿＿＿＿3、如图10-5，在矩形ABCD 中，AB ＝5，BC ＝12，将矩形ABCD 沿对角线对折，图10-1B 图10-2 D A EB C AD E B C F图10-3 图10-4A BCD E D ’图10-5然后放在桌面上，折叠后所成的图形覆盖桌面的面积是＿＿＿＿＿＿＿4、在一个圆形时钟的表面，OA 表示秒针，OB 表示分针（O 为两针的旋转中心）若现在时间恰好是12点整，则经过＿＿＿＿秒钟后，△OAB 的面积第一次达到最大。

专题17 相似三角形中的四心问题专练（一）班级：___________姓名：___________得分：___________一、选择题1.已知直角三角形的两条直角边长分别为3，4，则该三角形的重心与外心的距离为()A. 12B. 52C. 53D. 56【答案】D【分析】本题考查了勾股定理、直角三角形斜边上的中线性质、重心的性质；熟练掌握勾股定理和重心定理，熟记直角三角形的外心是斜边的中点是解题的关键．根据勾股定理求出斜边的长度，根据斜边中线长为斜边长的一半求出斜边的中线CD，由重心定理即可得出GD的长．【解答】解：如图所示：设D为AB的中点，连接CD，∵∠ACB=90°，∴斜边AB=√32+42=5，∴斜边AB的中线CD=12×5=52，∵直角三角形的外心就为直角三角形斜边上的中点，∴D为Rt△ABC的外心，∵重心是三角形中线的交点，故重心G在中线CD上，∴由重心定理得：GD=13CD=13×52=56．2.如图，点E为△ABC的内心，过点E作MN//BC交AB于点M，交AC于点N.若AB=7，AC=5，BC=6，则MN的长为()A. 3.5B. 4C. 5D. 5.5【答案】B【分析】连接EB、EC，如图，利用三角形内心的性质得到∠1=∠2，利用平行线的性质得∠2=∠3，所以∠1=∠3，则BM=ME，同理可得NC=NE，接着证明△AMN∽△ABC，所以MN6=7−BM7，则BM=7−76MN①，同理可得CN=5−56MN②，把两式相加得到MN的方程，然后解方程即可．本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．也考查了相似三角形的判定与性质．【解答】解：连接EB、EC，如图，∵点E为△ABC的内心，∴EB平分∠ABC，EC平分∠ACB，∴∠1=∠2，∵MN//BC，∴∠2=∠3，∴∠1=∠3，∴BM=ME，同理可得NC=NE，∵MN//BC，∴△AMN∽△ABC，∴MNBC =AMAB，即MN6=7−BM7，则BM=7−76MN①，同理可得CN=5−56MN②，①+②得MN=12−2MN，∴MN=4．3.在△ABC中，AC=6，AB=14，BC=16，点D是△ABC的内心，过D作DE//AC交BC于E，则DE的长为()A. 169B. 163C. 83D. 569【答案】C【分析】过点B作BH//AC，交AD的延长线于点H，由内心的性质可证AB=BH=14，DE=EC，通过证明△ACF∽△HBF，可求CF的长，通过证明△DEF∽△ACF，可求DE 的长．本题考查了相似三角形的判定和性质，三角形的内心的性质，利用相似三角形的性质求出CF的长是本题的关键．【解答】解：如图，过点B作BH//AC，交AD的延长线于点H，∵点D是△ABC的内心，∴∠BAD=∠CAD，∠ACD=∠DCB，∵DE//AC，BH//AC，∴∠H=∠DAC，∠EDC=∠ACD，∴∠H=∠BAD，∠EDC=∠ECD，∴AB=BH=14，DE=EC，∵BH//AC，∴△ACF∽△HBF，∴ACBH =CFBF，∴614=CF16−CF∴CF=245，∵DE//AC，∴△DEF∽△ACF，∴DEAC =EFFC，∴DE6=245−DE245∴DE=83，4.如图，已知点B，D在AC的两侧，E，F分别是△ACD与△ABC的重心，且EF=2，则BD的长度是()A. 4B. 5C. 6D. 7【答案】C【分析】本题考查三角形的重心的性质，相似三角形的判定和性质；解题的关键是作辅助线，灵活运用三角形重心的性质及相似三角形的判定与性质来解题，连接DE并延长，交AC于点O，连接BO.根据重心的性质得出FB=2FO，ED=2EO，再证明△EOF∽△DOB，根据相似三角形对应边成比例求出BD=3EF.【解答】解：如图，连接DE并延长，交AC于点O，连接BO．∵点E为△ADC的重心，∴点O为AC的中点，FB=2FO；又∵点F为△ABC的重心，∴点F在线段BO上，ED=2EO；∴OFOB =OEOD=13，又∵∠EOF=∠DOB，∴△EOF∽△DOB，∴EFBD =OFOB=OEOD=13，∴BD=3EF=6.5.如图，在△ABC中，点O为重心，则S△DOE：S△DCE=()A. 1：4B. 1：3C. 1：2D. 2：3【答案】B【分析】本题考查的是相似三角形的判定与性质，先根据题意得出DE是△ABC的中位线是解答此题的关键．利用三角形重心的定义得出D是AB的中点，E是AC的中点，根据题意判断出DE是△ABC的中位线，故可得出△ODE∽△OCB，由此可得出ODOC =12，进而可得出结论．【解答】解：由三角形重心的定义得出D是AB的中点，E是AC的中点，∵在△ABC中，两条中线BE，CD相交于点O，∴DE是△ABC的中位线，∴△ODE∽△OCB，∴ODOC =12，∴ODCD =13，∵△DOE与△DCE等高，∴S △DOE ：S △DCE =OD ：CD =1：3．6. 如图，点G 是△ABC 的重心，GD//BC ，则S △ADG :S △ABC 等于( )．A. 2:3B. 4:9C. 2:9D. 无法确定【答案】C【分析】此题主要考查了相似三角形的判定与性质和三角形重心的性质等知识，根据已知得出S ADG ：S △ANC =(23)2是解题关键．根据重心的性质得出AG GN =21，以及AG AN =23，即可得出S ADG ：S △ANC 的比值，再利用三角形中线的性质得出S △ANC =S △ABN ，进而得出答案．【解答】解：延长AG 到BC 于点N ，∵点G 是△ABC 的重心，GD//BC ，∴AG GN =21， ∴AG AN =23，∴S ADG ：S △ANC =(23)2=49，∵根据G 是△ABC 的重心，则AN 是三角形中线，∴S △ANC =S △ABN ，∴S ADG ：S △ABC =4：18=2：9．二、填空题7.如图，G是△ABC的重心，AG⊥GC，AC=4，则BG的长为__________．【答案】4【分析】本题考查了三角形重心，直角三角形斜边上的中线的性质，掌握三角形重心的定义是关键，延长BG交AC于D点，G是△ABC的重心，故BD为△ABC的中线；又AG⊥GC，AC，故GD为Rt△AGC斜边上的中线，根据直角三角形斜边上中线的性质可知GD=12即可得到BG=2GD=AC．【解答】解：如图，延长BG交AC于D点，∵G是△ABC的重心，∴BD为△ABC的中线，又∵AG⊥GC，∴GD为Rt△AGC斜边上的中线，∴GD=1AC，2∵G是△ABC的重心，∴BG=2GD=AC=4，8.如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D.AD与BC相交于点F，连结BE，DC，已知EF=2，CD=5，则AD=_____________．【答案】253【分析】本题考查的是三角形的内接圆与内心、外接圆与外心，掌握三角形的内心的定义、圆周角定理、相似三角形的判定定理和性质定理是解题的关键．根据三角形的内心的定义得到BD=CD，△BDF∽△ADB，根据相似三角形的性质列出比例式，代入计算即可．【解答】解：∵点E是△ABC的内心，∴∠BAD=∠CAD，∠ABE=∠CBE，∴BD⏜=CD⏜，∴BD=CD=5，由圆周角定理得，∠CAD=∠CBD，∵∠DBE=∠CBD+∠CBE，∠DEB=∠BAD+∠ABE，∴∠DBE=∠DEB.∴DE=DB=5，∴DF=DE−EF=3，∵∠DBC=∠BAD，∠BDF=∠ADB，∴△BDF∽△ADB，∴DFDB =DBAD，∴AD=BD2DF =253，9.如图，△ABC中，AB=AC=3√10，BC=6，且若CD经过△ABC的外心O交AB于D，则CD=______．【答案】9013【分析】延长AO交BC于F，作DE⊥BC于E，如图，证明AF垂直平分BC得到∠AFC= 90°，BF=CF=3，再利用勾股定理计算出AF=9，设⊙O的半径为r，则OC=OA=r，OF=9−r，根据勾股定理得到(9−r)2+32=r2，则可解得r=5，设DE=x，EF=y，根据平行线分线段成比例定理，由DE//AF得到DEAF =BEBF，则x=3(3−y)，由OF//DE得4 x =33+y，再利用代入消元求出y=1513，然后根据平行线分线段成比例定理，利用OF//DE可求出CD．本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．平行于三角形的一边，并且和其他两边(或两边的延长线)相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．也考查了三角形外心和等腰三角形的性质．【解答】解：延长AO交BC于F，作DE⊥BC于E，如图，∵AB=AC，OB=OC，∴AF垂直平分BC，∴∠AFC=90°，BF=CF=12BC=3，在Rt△ACF中，AF=√(3√10)2−32=9，设⊙O的半径为r，则OC=OA=r，OF=9−r，在Rt△OCF中，(9−r)2+32=r2，解得r=5，∴OF=4，设DE=x，EF=y，∵DE//AF，∴DEAF =BEBF，即x9=3−y3，则x=3(3−y)，∵OF//DE，∴OFDE =CFCE，4x=33+y，∴43(3−y)=33+y，解得y=1513，∵OF//DE，∴OCCD =CFCE，即5CD=33+1513，∴CD=9013．10.如图，点G是△ABC的重心，GE//BC，如果BC=12，那么线段GE的长为．【答案】4【分析】本题考查三角形的重心，属于基础题．先根据三角形重心性质得到AG=2GD，再证明△AGE∼△ADC，根据相似三角形的性质即可计算GE的长．【解答】解：因为点G是△ABC的重心，所以AG=2GD，BD=DC=12BC=6，因为GE//BC，所以△AGE∼△ADC，所以AGAD =GEDC，即GE6=23，所以GE=4．11.如图，点G是△ABC的重心，GH⊥BC，垂足为点H，若GH=6，则点A到BC的距离为______【答案】18【分析】本题考查的是相似三角形的判定与性质，三角形的重心有关知识，根据题意作图，利用重心的性质AD：GD=3：1，同时还可以求出△ADE∽△GDH，从而得出AD：GD=AE：GH=3：1，根据GH=6即可得出答案．【解答】解：设BC的中线是AD，BC的高是AE，由重心性质可知：AD：GD=3：1，∵GH⊥BC，∴△ADE∽△GDH，∴AD：GD=AE：GH=3：1，∴AE=3GH=3×6=18，三、解答题12.如图，在4×4的方格中，点A，B，C为格点．(1)利用无刻度的直尺在图1中画△ABC的中线BE和重心G；(2)在图2中标注△ABC的外心O并画出外接圆及切线CP．【分析】(1)根据中线的概念作图；(2)根据线段垂直平分线的定义作图．本题主要考查作图−应用与设计作图，解题的关键是掌握三角形的高线、中线以及角平分线的定义．【解答】解：(1)如图所示，BE和点G即为所求；(2)如图所示，⊙O和PC即为所求．13.已知：如图1，△ABC中，∠ACB=90°，AC=BC，CD⊥AB于点D，∠CAB的三等分线AE、AF分别与CD交于点E、F，连结BE并延长与AC交于点M，连结MF并延长与BC交于点N．(1)求∠ABE的度数；(2)求证：点F是△BCM的内心；(3)如图2，若AB=4，点Q为线段BC上一动点，点P是平面内一点，且∠PDQ=90°，DP DQ =12，当点Q从点C运动到点B时，求点P运动的路径长．【分析】本题主要考查了相似三角形的判定与性质，掌握住相似三角形的判定与性质是解答的关键．(1)根据已知∠ACB=90°，AC=BC，得出CD是△ABC的对称轴，从而找出∠CAB的三等分线，求出∠ABE的度数；(2)依据三线合一得出∠CAB的三等分线，由对称的性质得出BF是∠MBC的平分线，从而得出结论；(3)由点H是BD的中点得出BD=CD，然后依据比值得出DHCD =DPDQ，再找出∠CDQ=∠HDP，从而得出△HDP∽△CDQ，然后依据相似三角形的性质逐步解答即可．【解答】解：(1)∵∠ACB=90°，AC=BC，∴∠CAB=∠CBA=45°，∵CD⊥AB于点D，∴直线CD是△ABC的对称轴，∴∠ABE=∠BAE，∴AE、AF是∠CAB的三等分线，∴∠BAE=15°，∴∠ABE=15°；(2)连结BF，由三线合一可知CD是∠ACB的角平分线，∴AE、AF是∠CAB的三等分线，∴AF是△AEC的角平分线，根据轴对称的性质可得：BF是∠MBC的平分线，∴点F是△BCM的内心；(3)取BD的中点H，连接HP，∵点H是BD的中点，BD=CD，∴DHCD =12，∴DPDQ =12，∴DHCD =DPDQ，∵CD⊥AB，∠PDQ=90°，∴∠CDQ+∠QDB=90°，∠QDB+∠HDP=90°，∴∠CDQ=∠HDP，∴△HDP∽△CDQ，∴∠DHP=∠DCQ=45°，HPCQ =12，∴点P运动的路径是线段，且路径长等于CQ的一半，∵AB=4，∴BC=2√2，∴点P运动的路径长为√2．14.如图，在△ABC中，AD为边BC上的中线，且AD平分∠BAC.嘉淇同学先是以A为圆心，任意长为半径画弧，交AD于点P，交AC于点Q，然后以点C为圆心，AP长为半径画弧，交AC于点M，再以M为圆心，PQ长为半径画弧，交前弧于点N，作射线CN，交BA的延长线于点E．(1)通过嘉淇的作图方法判断AD与CE的位置关系是______，数量关系是______；(2)求证：AB=AC；(3)若BC=24，CE=10，求△ABC的内心到BC的距离．【答案】(1)AD//CE；EC=2AD；(2)证明：∵AD//CE，∴∠BAD=∠E，∠DAC=∠ACE，∵AD平分∠BAC，∴∠BAD=∠DAC，∴∠ACE=∠E，∴AC=AE，由(1)知△ABD∽△EBC，∴ABEB =BDBC=12，∴EB=2AB，即AB=AE，∴AB=AC．(3)解：∵BC=24，CE=10，∴BD=12，AD=5，∵AB=AC，BD=CD，∴AD⊥BD，设△ABC内心到BC距离为r，∴ABBD =5−rr，∴5−r13=r12，∴60−12r=13r∴25r=60，∴r=125．【分析】(1)由作图方法可知∠DAC=∠ACE，则AD//CE，根据BC=2BD，可证CE=2AD；(2)由(1)知△ABD∽△EBC，证出BE=2AB，得AB=AE，又AC=AE，则AB=AC；(3)设△ABC内心到BC距离为r，可得ABBD =5−rr，即可求出r．本题是圆的综合题目，考查了内心的定义、等腰三角形的性质、相似三角形的判定与性质、勾股定理等知识．【解答】解：(1)∵嘉淇的作图方法可知∠DAC=∠ACE，∴AD//CE，∴△ABD∽△EBC，∴BDBC =ADCE，∵AD为边BC上的中线，∴BC=2BD，∴CE=2AD，故答案为：AD//CE，EC=2AD；(2)证明：∵AD//CE，∴∠BAD=∠E，∠DAC=∠ACE，∵AD平分∠BAC，∴∠BAD=∠DAC，∴∠ACE=∠E，∴AC=AE，由(1)知△ABD∽△EBC，∴ABEB =BDBC=12，∴EB=2AB，即AB=AE，∴AB=AC．(3)解：∵BC=24，CE=10，∴BD=12，AD=5，∵AB=AC，BD=CD，∴AD⊥BD，设△ABC内心到BC距离为r，∴ABBD =5−rr，∴5−r13=r12，∴60−12r=13r∴25r=60，∴r=125．15.如图：AB是⊙O的直径，AC交⊙O于G，E是AG上一点，D为△BCE内心，BE交AD于F，且∠DBE=∠BAD．(1)求证：BC是⊙O的切线；(2)求证：DF=DG；(3)若∠ADG=45°，DF=1，则有两个结论：①AD⋅BD的值不变；②AD−BD的值不变，其中有且只有一个结论正确，请选择正确的结论，证明并求其值．【分析】(1)先证∠DBC=∠BAD，再证∠DBC+∠ABD=90°，即∠ABC=90°，可得出结论；(2)如图1，连接DE，分别证∠BFD=∠ABD，∠BFD=∠DGC，则∠DFE=∠DGE，因为D为△BCE内心，所以∠DEG=∠DEB，可得△DEF≌△DEG，即可得出结论；(3)先判断AD−BD的值不变，如图2，在AD上截取DH=BD，连接BH、BG，先证AB=√2BG，BD=DH，再证△ABH∽△GBD，求出AH的长，即可证明AD−BD=2．本题考查了圆的有关概念及性质，切线的判定定理，全等三角形的判定与性质，相似三角形的判定与性质等，综合性质较强，解题关键是能够熟练掌握各方面的知识，并能够灵活运用圆的有概念及性质和相似三角形的判定与性质等．【解答】(1)证明：∵D为△BCE内心，∴∠DBC=∠DBE，∵∠DBE=∠BAD．∴∠DBC=∠BAD，∵AB是⊙O的直径，∴∠ADB=90°，∴∠BAD+∠ABD=90°，∴∠DBC+∠ABD=90°，即∠ABC=90°，∴AB⊥BC，∴BC是⊙O的切线；(2)证明：如图1，连接DE，∵∠DBC=∠BAD，∠DBC=∠DBE，∴∠DBE=∠BAD，∴∠ABF+∠BAD=∠ABF+∠DBE，∴∠BFD=∠ABD，∵∠DGC=∠ABD，∴∠BFD=∠DGC，∴∠DFE=∠DGE，∵D为△BCE内心，∴∠DEG=∠DEB，在△DEF和△DEG中{∠DFE=∠DGE ∠DEG=∠DEF DE=DE，∴△DEF≌△DEG(AAS)，∴DF=DG；(3)解：AD−BD的值不变；如图2，在AD上截取DH=BD，连接BH、BG，∵AB是直径，∴∠ADB=∠AGB=90°，∵∠ADG=45°，∴∠ABG=∠ADG=45°，∴AB=√2BG，∵∠BDH=90°，BD=DH，∴∠BHD=45°，∴∠AHB=180°−45°=135°，∵∠BDG=∠ADB+∠ADG=90°+45°=135°，∴∠AHB=∠BDG，∵∠BAD=∠BGD，∴△ABH∽△GBD，∴AHDG =ABBG=√2，∵DG=1，∴AH=√2，∵AD−BD=AD−DH=AH，∴AD−BD=√2．16.如图1，P为△ABC内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．(1)如图2，已知Rt△ABC中，∠ACB=90°，∠ABC>∠A，CD是AB上的中线，过点B作BE⊥CD，垂足为E.试说明E是△ABC的自相似点；(2)在△ABC中，∠A<∠B<∠C．(i)如图3，利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹)；(ii)若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．(内心是三角形三个内角的角平分线交点)【分析】此题主要考查了相似三角形的判定以及三角形的内心作法和作一角等于已知角，此题综合性较强，注意从已知分析获取正确的信息是解决问题的关键．(1)根据已知条件得出∠BEC=∠ACB，以及∠BCE=∠ABC，得出△BCE∽△ABC，即可得出结论；(2)(i)根据作一角等于已知角即可得出△ABC的自相似点；(ii)根据∠PBC=∠A，∠BCP=∠ABC=∠2∠PBC=2∠A，∠ACB=2∠BCP=4∠A，即可得出各内角的度数．【解答】解：(1)在Rt△ABC中，∠ACB=90°，CD是AB上的中线，∴CD=12AB，∴CD=BD，∴∠BCE=∠ABC，∵BE⊥CD，∴∠BEC=90°，∴∠BEC=∠ACB，∴△BCE∽△ABC，∴E是△ABC的自相似点；(2)(i)如图所示，作法：①在∠ABC内，作∠CBD=∠A，②在∠ACB内，作∠BCE=∠ABC，BD交CE于点P，则P为△ABC的自相似点；(ii)∵P是△ABC的内心，∴∠PBC=12∠ABC，∠PCB=12∠ACB，∵△ABC的内心P是该三角形的自相似点，∴∠PBC=∠A，∠BCP=∠ABC=2∠PBC=2∠A，∠ACB=2∠BCP=4∠A，∴∠A+2∠A+4∠A=180°，∴∠A=180°7，∴该三角形三个内角度数为：180°7，360°7，720°7．17.我们知道：三角形三条角平分线的交点叫做三角形的内心，已知点I为△ABC的内心(1)如图1，连接AI并延长交BC于点D，若AB=AC=3，BC=2，求ID的长(2)过点I作直线交AB于点M，交AC于点N．①如图2，若MN⊥AI，求证：MI2=BM•CN②如图3，AI交BC于点D，若∠BAC=60°，AI=4，求1AM +1AN的值．【分析】本题考查三角形综合题、相似三角形的判定和性质、三角形的内心、角平分线的性质、平行线的性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，属于中考压轴题．(1)如图1中，作IE⊥AB于E.设ID=x.由△BEI≌△BDI，可得ID=IE=x，BD=BE=1，AE=2，在Rt△AEI中，根据AE2+EI2=AI2，可得方程，解方程即可；(2)如图2中，连接BI、CI.首先证明△AMI≌△ANI(ASA)，再证明△BMI∽△INC，可得NI2=BM⋅CN，由此即可解决问题；(3)过点N作NG//AD交MA的延长线于G.由∠ANG=∠AGN=30°，推出AN=AG，NG，由AI//NG，推出比例式，即可求得答案．【解答】解：(1)如图1中，作IE⊥AB于E.设ID=x．∵AB=AC=3，AI平分∠BAC，∴AD⊥BC，BD=CD=1，在Rt△ABD中，AD=√AB2−BD2=√32−12=2√2，∵∠EBI=∠DBI，∠BEI=∠BDI=90°，BI=BI，∴△BEI≌△BDI，∴ID=IE=x，BD=BE=1，AE=2，在Rt△AEI中，∵AE2+EI2=AI2，∴22+x2=(2√2−x)2，∴x=√22，∴ID=√22．(2)如图2中，连接BI、CI．∵I是内心，∴∠MAI=∠NAI，∵AI⊥MN，∴∠AIM=∠AIN=90°，∵AI=AI，∴△AMI≌△ANI(ASA)，∴∠AMN=∠ANM，∴∠BMI=∠CNI，设∠BAI=∠CAI=α，∠ACI=∠BCI=β，∴∠NIC=90°−α−β，∵∠ABC=180°−2α−2β，∴∠MBI=90°−α−β，∴∠MBI=∠NIC，∴△BMI∽△INC，∴BMNI =NINC，∴NI2=BM⋅CN，∵NI=MI，∴MI2=BM⋅CN．(3)过点N作NG//AD交MA的延长线于G．∴∠ANG=∠AGN=30°，∴AN=AG，NG=√3AN，∵AI//NG，∴AMMG =AING，∴AMAM+AN =√3AN，∴1AM +1AN=√34．。

专题:平面向量与三角形四心问题三角形四心指的是三角形的垂心、重心、内心和外心，在高考中常常结合平面向量的知识进行考察，是高中数学的一个难点.很多学生对三角形四心总是产生混淆，面对与四心有关的问题也常常束手无策，为了解决广大学子的困扰，本文以四心的常见结论出发，借助几道经典的例题，对三角形四心问题进行系统梳理，希望能够为读者提供帮助.如果读者是在校高中生，则标注了星号的内容可作为拓展知识. 一、三角形的内心（1）定义：三角形内切圆的圆心，即三角形三条角平分线的交点（如图1）. （2）向量表示：若O 为△ABC 的内心→→→→=⋅+⋅+⋅⇔0OC c OB b OA a . （注：本文中的边a ，b ，c 分别表示BC ，AC ，AB .角A ，B ，C 分别表示BAC ∠，ABC ∠，ACB ∠.）证明：→→→→→→→→→→=+⋅++⋅+⋅⇔=⋅+⋅+⋅0)()(0AC OA c AB OA b OA a OC c OB b OA a→→→→=⋅+⋅+⋅++⇔0)(AC c AB b OA c b a →→→⋅+⋅=⋅++⇔AC c AB b AO c b a )(||||||||)(→→→→→→→⋅⋅+⋅⋅=⋅++⇔AC AC AC c AB AB AB b AO c b a)||||()(→→→→→+⋅=⋅++⇔AC ACAB ABbc AO c b a)||||(→→→→→+⋅++=⇔AC ACAB AB c b a bc AO （图1）⇔点O 在角A 的角平分线上，同理点O 也在角B 、C 的角平分线上. ⇔O 为△ABC 的内心.（3）常用性质性质1：))(||||(R AC ACAB AB∈+⋅→→→→λλ所在的直线与A ∠的角平分线重合（经过内心）.证明：如图所示，||→→AB AB 表示→AB 上的单位向量，不妨记作→AD ，||→→AC AC 表示→AC 上的单位向量，不妨记作→AE .设→→→+=AE AD AP ，由平行四边形法则知，四边形ADPE 为菱形， 故直线AP 为A ∠的角平分线.))(||||(RAC ACAB AB∈+⋅∴→→→→λλ所在的直线与A ∠的角平分线重合（经过内心）.性质2：r c b a S ABC ⋅++=∆)(21（r △ABC 内切圆的半径）. 证明：由等面积法易证.性质3：O 为△ABC 的内心c b a S S S OAB OAC OBC ::::=⇔∆∆∆. 证明：由面积公式易证. （4）典例剖析例1-1：在△ABC 中，O 为平面内一个定点，动点P 满足)||||(→→→→→→++=AC ACAB ABOA OP λ,),0(+∞∈λ.则动点P 的轨迹经过△ABC 的（ ）A .内心B .外心C .垂心D .重心 解析：由性质1知，答案为A .例1-2：已知O 是△ABC 所在平面上的一点，若cb a PCc PB b PA a PO ++++=→→→→（其中P 是△ABC 所在平面内任意一点），则O 是△ABC 的（ ）A .内心B .外心C .垂心D .重心 解析：由题意知→→→→→→++=++PC c PB b PA a PO c PO b aPO ，即+-→→)(PO PA a→→→→→=-+-0)()(PO PC c PO PB b ，化简得→→→→=⋅+⋅+⋅0OC c OB b OA a .根据内心的向量表示知，O 是△ABC 的内心，答案为A .例1-3：已知O 是△ABC 内的一点，且满足0)||||(=-⋅→→→→→AC ACAB ABOA ，则OA 所在的直线一定经过三角形的（ ）A .内心B .外心C .垂心D .重心解析：||→→AB AB 表示→AB 上的单位向量，不妨记作→1e ，||→→AC AC 表示→AC 上的单位向量，不妨记作→2e .故0)(21=-⋅→→→e e OA ，即→→→→⋅=⋅21e OA e OA ,即>>=<<→→→→21,,e OA e OA .∴直线OA 与A ∠的角平分线重合，故OA 所在的直线一定经过三角形的内心，答案A .二、三角形的外心（1）定义：三角形外接圆的圆心，即三角形三边中垂线的交点（如图2）. （2）向量表示：若O 为△ABC 的外心||||||→→→==⇔OC OB OA . （3）常用性质：奔驰定理*：已知O 为△ABC 内的一点（不一定为外心）， 则→→∆→∆→∆=⋅+⋅+⋅0OC S OB S OA S OAB OAC OBC .（该定理反之也成立）证明：不妨延长AO 到D （如下图），则 （图2）=++===∆∆∆∆∆∆∆∆ACD ABD OAC OAB ACD OAC ABD OAB S S S S S S S S AD AO ABC OACOAB S S S ∆∆∆+， 即→∆∆∆→+=AD S S S AO ABCOAC OAB .且根据B ，D ,C 三点共线知，→∆∆∆→∆∆∆→+++=AB S S S AC S S S AD OAC OAB OACOAC OAB OAB ，故→∆∆→∆∆→+=AB S S AC S S AO ABC OAC ABC OAB ，即)()(→→∆∆→→∆∆→-+-=-OA OB S S OA OC S S OA ABCOAC ABC OAB . →→∆→∆→∆=⋅+⋅+⋅∴0OC S OB S OA S OAB OAC OBC （反之易证）性质1*：O 为△ABC 的外心C B A S S S OAB OAC OBC 2sin :2sin :2sin ::=⇔∆.证明：如图2所示，O 为△ABC 的外心A R BOC R S OBC 2sin 212sin 2122=∠=⇔∆，B R AOC R S OAC 2sin 212sin 2122=∠=∆，C R AOB R S OAB 2sin 212sin 2122=∠=∆ C B A S S S OAB OAC OBC 2sin :2sin :2sin ::=⇔∆（R 为△ABC 外接圆半径）.性质2*：O 为△ABC 的外心→→→→=⋅+⋅+⋅⇔0)2(sin )2(sin )2(sin OC C OB B OA A . 证明：结合性质1与奔驰定理易证.（4）典例剖析例2-1：在△ABC 中，O 为平面内一个定点，动点P 满足++=→→→2OCOB OP )cos ||cos ||(CAC AC BAB AB →→→→+λ，),0(+∞∈λ.则动点P 的轨迹一定经过△ABC 的（ ）A .内心B .外心C .垂心D .重心 解析：设线段BC 的中点为D ，故)cos ||cos ||(C AC AC BAB AB OD OP →→→→→→++=λ，即)cos ||cos ||(CAC AC BAB AB DP →→→→→+=λ,而)cos ||cos ||(CAC BC AC BAB BC AB BC DP →→→→→→→→⋅+⋅=⋅λ，即)cos ||cos ||||cos ||)cos(||||(CAC CBC AC B AB B BC AB BC DP →→→→→→→→⋅+-⋅=⋅πλ0|)|||(=+-=→→BC BC λ 即→→⊥BC DP ，故点P 在线段BC 的垂直平分线上. ∴动点P 的轨迹一定经过△ABC 的外心，答案B .例2-2：在△ABC 中，动点O 满足→→→→⋅=-BC AO AB AC 222，则点O 一定经过△ABC 的（ ）A .内心B .外心C .垂心D .重心解析：由题知→→→→→→⋅=+-BC AO AB AC AB AC 2))((，设D 为BC 的中点，则=⋅→→AD BC 2→→⋅BC AO 2,故0=⋅→→OD BC ,即→→⊥OD BC ，O ∴在BC 的垂直平分线上，故点O 一定经过△ABC 的外心，答案B .例2-3：已知O 为△ABC 所在平面内的一点，满足→→→→⋅=⋅BA OB AB OA ，=⋅→→BC OB→→⋅CB OC ，则O 为△ABC 的（ ）A .内心B .外心C .垂心D .重心解析：由→→→→⋅=⋅BA OB AB OA 知0)(=+⋅→→→OA OB AB ,即0)()(=+⋅-→→→→OA OB OA OB ，即||||→→=OA OB ,同理可得：||||→→=OC OB ，O ∴为△ABC 的外心，答案B .三、三角形的垂心（1）定义：三角形三条高的交点（如图3）.（2）向量表示：若O 为△ABC 的垂心→→→→→→⋅=⋅=⋅⇔OC OB OC OA OB OA . 证明：→→→→→→→→→→→⊥⇔=⋅=-⋅⇔⋅=⋅BC OA BC OA OB OC OA OC OA OB OA 0)(.同理→→⊥AC OB ,O AB OC ⇔⊥→→为△ABC 的垂心.（3）常用性质性质1*：O 为锐角△ABC 的垂心⇔=∆∆∆OAB OAC OBC S S S ::C B A tan :tan :tan . （图3）证明：ACDOC b BCDOC a OF b OE a S S OAC OBC ∠⋅⋅∠⋅⋅=⋅⋅=∆∆sin sin ,且在直角△BCD 和直角△ACD 中有 B BCD cos sin =∠，A ACD cos sin =∠.故BAA B B A A b B a S S OAC OBC tan tan cos sin cos sin cos cos =⋅⋅=⋅⋅=∆∆. 同理，CBS S OAB OAC tan tan =∆∆. C B A S S S OAB OAC OBC tan :tan :tan ::=∴∆∆∆，反之易证.性质2*：当O 为锐角△ABC 的垂心→→→→=⋅+⋅+⋅⇔0tan tan tan C OC B OB A OA .证明：利用性质1和“奔驰定理”易证. （4）典例剖析例3-1：在△ABC 中，O 为平面内一个定点，动点P 满足)cos ||cos ||(CAC AC BAB AB OA OP →→→→→→++=λ，),0(+∞∈λ，则动点P 的轨迹一定经过△ABC 的（ ）A .内心B .外心C .垂心D .重心 解析：由题知)cos ||cos ||(CAC AC BAB AB AP →→→→→+=λ,得=⋅+-⋅=⋅+⋅=⋅→→→→→→→→→→→→→→)cos ||cos ||||cos ||)cos(||||()cos ||cos ||(CAC CBC AC B AB B BC AB CAC BC AC BAB BC AB BC AP πλλ0|)|||(=+-→→BC BC λ，即→→⊥BC AP .P ∴在BC 边上的高上，过垂心，答案C .例3-2：已知O 为△ABC 所在平面内的一点，且满足=+=+→→→→2222||||||||AC OB BC OA22||||→→+AB OC ,则O 是△ABC 的（ ）A .内心B .外心C .垂心D .重心 解析：由题知2222||||||||→→→→-=-BC AC OB OA ，即=+⋅-→→→→)()(OB OA OB OA)()(→→→→+⋅-BC AC BC AC ，即0)()(=+⋅++⋅→→→→→→OB OA AB BC AC AB ,即02=⋅→→OC AB ，故→→⊥OC AB ，同理→→⊥OB AC ，→→⊥OA BC∴O 是△ABC 的垂心，答案C .例3-3：设O 是△ABC 的外心，点P 满足→→→→=++OP OC OB OA ,则P 是△ABC 的（ ）A .内心B .任意一点C .垂心D .重心 解析：由题知→→→→→=-=+CP OC OP OB OA ，由于O 是△ABC 的外心，故→→→=+OD OB OA 2（D 为线段AB 的中点）且→→⊥AB OD ，即→→=OD CP 2，→→⊥∴AB CP ，同理→→⊥AC BP ，→→⊥BC AP ，故P 是△ABC 的垂心，答案C .四、三角形的重心（1）定义：三角形三条中线的交点（如图4）.（2）向量表示：若O 为△ABC 的重心→→→→=++⇔0OC OB OA . （3）常用性质 （ 图4 ）性质1：若O 为△ABC 的重心ABC OBC OAC OAB S S S S ∆∆∆∆===⇔31性质2：若O 为△ABC 的重心→→=⇔AF AO 32，→→=BD BO 32，→→=CF CO 32性质3：已知),(11y x A ，),(22y x B ,),(33y x C .若O 为△ABC 的重心)3,3(321321y y y x x x O ++++⇔.（4）典例剖析例4-1：在△ABC 中，O 为平面内一个定点，动点P 满足)sin ||sin ||(CAC AC BAB AB OA OP →→→→→→++=λ，),0(+∞∈λ，则动点P 的轨迹一定经过△ABC的（ ）A .内心B .外心C .垂心D .重心 解析：由题知)sin ||sin ||(CAC AC BAB AB AP →→→→→+=λ，其中hC AC B AB ==→→sin ||sin ||（h 表示BC 边上的高），故)(hACh AB AP →→→+=λ→=AF h λ2（F 为线段BC 的中点）. P ∴在BC 边上的中线上，故动点P 的轨迹一定经过△ABC 的重心，答案D .例4-2：在△ABC 中，O 为平面内一个定点，动点P 满足])21()1()1[(31→→→→++-+-=OC OB OA OP λλλ，R ∈λ，则动点P 的轨迹一定经过△ABC 的（ ）A .内心B .外心C .垂心D .重心解析：设AB 的中点为D ，故])21()1(2[31→→→++-=OC OD OP λλ，由于+-3)1(2λ1321=+λ，即点P ，C ，D 三点共线. P ∴在AB 边上的中线上，故动点P 的轨迹一定经过△ABC 的重心，答案D .例4-3：已知O 在△ABC 内，且满足→→→→=++0432OC OB OA ，现在到△ABC 内随机取一点，次点取自△OAB ，△OAC ，△OBC 的概率分别记为1P 、2P 、3P ,则（ ）A .321P P P ==B .123P P P >>C .321P P P >>D .312P P P >> 解析：法一：如图，延长OA ，OB ，OC 使得OA OD 2=,OB OE 3=，OC OF 4=, 故→→→→=++0OF OE OD ，即O 是△DEF 的重心，即△OED 、△ODF 、 △OEF 的面积相等，不妨令它们的面积都为1. 61=∴∆OAB S ，81=∆OAC S ，121=∆OBC S ,故321P P P >>，答案C . 法二：由“奔驰定理”知，k S OBC 2=∆，k S OAC 3=∆，kS OAB 4=∆（k 为比例系数），故321P P P >>，答案C .法三：根据三角形内心的向量表示，不妨设O 是以2k ，3k ，4k （k 为比例系数）为边长的三角形的内心，所以OBC OAC OAB S S S ∆∆∆>>,即321P P P >>，答案C .五、等腰（边）三角形的四心 （1）等腰三角形等腰三角形只有顶角的角平分线与中线、高三线重合，其余的线不重合.另外，等腰三角形的四心不重合. （2）等边三角形性质1：若△ABC 为等边三角形⇔△ABC 四心合一. 性质2：若△ABC 为等边三角形⇔△ABC 三线合一. 六、欧拉线*瑞士数学家欧拉（1707~1783）于1765年在他的著作《三角形 的几何学》中首次提出：（如图5）任意△ABC （非等边三角形）的垂心D 、重心E 、外心F 三点共线，即欧拉线. （图5）特别地，（如图6）当△ABC 为直角三角形时（A 为直角），垂心D 与A 重合，外心F 在BC 的中点上，欧拉线为直角△ABC 的外接圆半径（或BC 边上的中线）.（图6）性质1：在任意三角形中，垂心与重心的距离是重心与外心距离的2倍，即EF DE 2=.。

三角形的“四心”练习三角形是几何学中的基本图形之一，它具有丰富的性质和特点。

在三角形中，存在着四个特殊的点，被称为“四心”。

它们分别是垂心、重心、外心和内心。

本文将针对这四个心进行练习和探究。

垂心是三角形三条高线的交点，它与三角形的顶点相连，形成了三条互相垂直的直线。

我们以一个具体的例子来进行实践。

假设三角形ABC中，AB = 5cm，BC = 6cm，AC = 7cm。

首先，我们需要确定三个顶点A、B、C的坐标。

假设A点坐标为(0, 0)，B点坐标为(5, 0)，C点坐标为(3.5, 4)。

接下来，我们绘制出三角形ABC，并求出垂心H的坐标。

通过计算，得出三角形ABC的三边的中点分别为D(2.5, 0)、E(4.25, 2)和F(1.75, 2)。

然后，我们通过计算斜率，得出垂直于三边的直线方程，分别为x = 4.25、x = 1.75和y = 2。

将这三条直线带入到相交点的方程中，我们可以得出垂心H的坐标为(3, 1.33)。

在本次练习中，我们通过确定三个顶点的坐标，计算三边的中点，并求出相互垂直的直线方程，最终得出了垂心H的坐标。

接下来，我们将对重心进行练习。

重心是三角形三条中线的交点，它将三角形等分成六个小三角形。

同样以例子来进行实践。

依旧以三角形ABC，我们可以通过绘制出三角形ABC，并求出重心G的坐标。

通过计算，得出三角形ABC的三边的中点分别为D(2.5, 0)、E(4.25, 2)和F(1.75, 2)。

我们通过计算两个点的中点，得到DF中点M的坐标为(2.25, 1)。

同样地，我们计算出AE中点N的坐标为(2.75, 1)和BC中点P的坐标为(4, 2)。

将这三个中点带入到相交点的方程中，我们可以得出重心G的坐标为(3, 1)。

在本次练习中，我们通过确定三个顶点的坐标，计算三边的中点，并求出相互交点的方程，最终得出了重心G的坐标。

接下来，我们将对外心进行练习。

外心是三角形外接圆的圆心，它与三个顶点的距离都相等。

第十九讲三角形的四心【趣题引路】你知道欧拉线吗?欧拉线是欧拉发现的.欧拉(1707-1783),瑞士数学家,•变分法的奠基人,复变函数论的先驱者,理论流体力学的创始人,受学于贝努利家族.著作浩如烟海.几乎每一个数学分支都可见到他的名字.如多面体的欧拉定理,•空间解析几何的欧拉变换公式,四方方程的欧拉解法,数论中的欧拉函数,•微分方程中的欧拉方程,等等.他在数论和微分方程等方面有重大成就,•在天文学和物理学等方面也有很大贡献,对航海和弹道研究起了一定作用 .初等几何中的欧拉线.欧拉线定理的内容是:三角形任一顶点到垂心的距离等于外心到对边的距离的两倍,且三角形的外心、重心、垂心共线.你会证明这个定理吗?证明 (1)连BO交圆于E,则BE是直径,如图1,BO=OE,做OD⊥BC•于点D,•则BD=DC.∴OD//12EC.∵BE是直径.∴CE⊥BC,EA⊥AB.∴CE∥AH.AE∥CH,AHCE是平行四边形.∴AH//EC,∴AH=2OD;（1）（2） (2)△ABC中,AE为高,H为垂心,O为外心如图2.OD⊥BC于点D,连AD交HO于G′.∵AH//2OD,∴△AHG′∽△DOG′.∴AG′=2G′D.又∵AD是中线,∴G′与△ABC重心重合.∴三角形的外心,重心,•垂心三点共线.即H、G′、O共线.【知识延伸】三角形的四心,指的是外心、内心、重心、垂心.•由于三角形的四心处在特殊的位置上,因而它们具有独特的性质.这些是解与四心相关问题的基础.外心是三角形外接圆的圆心,它是三角形各边中垂线的交点.若O 为锐角△ABC•的外心,则有(1):∠BOC=2∠BAC,或∠BOC=360°-2∠A;(2)OA=OB=OC.内心是三角形三条内角平分线的交点,它是三角形内切圆的圆心.如I 是△ABC•的内心.则有:(1)∠BIC=90°+12∠A; (2)内切圆半径与半周长的积为三角形面积; (3)•内心I 到△ABC 的三边距离相等;(4)若延长AI 交△ABC 的外接圆于点E,则EI=EB=EC.(5)•在Rt △ABC 中,斜边为c,内切圆半径为r,两直角边分别为a 、b,则r=12(a+b+c). 重心是三角形三条中线的交点,设G 是△ABC 的重心,则有: (1)重心G•分每条中线为2:1; (2)S △BCG =S △CAG =S △ABC ;(3)若AD 是△ABC 的BC 边上的中线,•则有AD 2=12(AB 2+AC 2- BC 2).这就是中线长公式.(称斯台沃特定理).垂心是三角形三条高所在直线的交点,•常利用它构造相似三角形及判定四点共圆. 例1 已知G 、L 、H 分别是△ABC 的重心,内心,垂心,且AB>AC,则关系式: 甲: S △AGB > S △AGC ;乙: S △ALB > S △ALC ; 丙: S △ABC = S △AHC + S △BHC + S △AHC . 其中正确的有( )A.0个B.1个C.2个D.3个解析 如图3,若G 为△ABC 的重心.由重心的性质知, S △AGB = S △AGC .(3) (4) 如图4 ,若L 为△ABC 的内心,设三角形内切圆半径为r, 则S △ALC =12AB ·r. S △ALC =12AC ·r.∵AB>AC,∴S △ALB > S △ALC .当△ABC 为钝角三角形时,若H 为△ABC 的垂心,显然S △ABC ≠S △AHC + S △BHC+ S △BHA . 故选B. 点评利用重心、内心、垂心的性质,用排除法排除了甲和丙不成立,最后确定乙成立. 例2 如图,在Rt △ABC 中,∠A=90°,BC=a,CA=b,AB=c,I 为其内心,则tan 2B +tan 2C 的值为( ). A.2a a b c ++ B.aa b c ++C.22a a b c++ D.以上答案均不对 解析 连BI,AI,CI,过I 分别作三边的垂线ID,IE,IF,垂足分别为点D 、E 、F,•设△ABC 的内切圆I 的半径为r,则ID=IE=IF=r.在Rt △CIF 中,tan 2C =rCE .在Rt △BIF 中,tan 2B rBF=,∴tan 2B +tan 2C =r rCF BF +=()BF CF r BF CF +=ar BF CF.由切线长可知:CF+BF=a,CE+AE=b,AD+BD=c.又∵CE=CF,AD=AE,BD=BF,∴CF=12(a+b-c),BF=12(a+c-b). ∴CF ·BF=12(a+b-c)(a+c-b)=14[a 2-(c-b )2]=14[b 2+c 2-(c-b)2]=12bc.又∵12bc= (a+b+c)r =S △ABC ,∴bc=(a+b+c)r.∴BF ·CF=12(a+b+c)r. ∴tan 2B +tan 2C =2ara b c r ++=2a a b c ++.选A.点评由于I 为内心,由2B , 2C联想到连结BI,IC.在Rt △ABC 中用BF,CF 来表示出tan 2B ,tan 2C的值.再利用切线长定理表示出CF,BF 的长.【好题妙解】佳题新题品味例1 如图,△ABC 的外接圆为⊙O,∠ACB=60°,N 是弧AB 的中点,H 是垂心. 求证:CN ⊥OH.证明 连OC 、ON,延长AH 交⊙O 于H ′,连OH ′,CH ′. 由∠ACB=60°,得∠CAH ′=•30°, ∴∠COH ′=2∠CAH ′=60°.∵OC=OH ′,∴△OCH ′是正三角形,即OC=OH ′=CH ′. ∵AH ⊥BC,CH ⊥AB.∴B 、•Q 、H 、P 四点共圆,得∠CHH ′=∠CBA. 又∠CH ′B=∠CBA,从而知∠CHH ′=∠CH ′A,• 于是△CHH ′为等腰三角形.且有CH=CH ′. 由于H 为垂心,N 为AB 的中点. ∴CH ⊥AB,ON ⊥AB,从而得CH ∥OH.又ON=OC=CH ′=CH,由此知四边形OCHN 为菱形. ∴OH ⊥CN. 点评本题设法证明OH,CN 是菱形的对角线,从而使问题获证.例2 在△ABC 中,BC=a,AC=b,AB=c,∠ACB=90°,CD 和BE 是△ABC 的两条中线,•且CD ⊥BE,求a:b:c.解析 如图,设CD 、BE 相交于点F,则F 为△ABC 的重心.设EF=x,DF=y,•则FB=2x,CF=2y. 在Rt △BCE 中,∵CF ⊥BE,∴Rt △BCF ∽Rt △BEC, ∴a 2=2x ·3x=6x 2.同理,(12b )2=x ·3x, 即b 2=12x 2.在Rt △DFB 中,由勾股定理,得 (12c )2=(2x)2+y 2,∴c 2=16x 2+4y 2. ① 又∵Rt △FEC ∽Rt △FCB,∴C F 2=EF ·BF.即(2y 2)=x ·2x,∴y 2=12x 2. ②以②式代入①得c 2=18x 2,∴a 2:b 2:c 2=6x 2:12x 2:18x 2=1:2:3 ∴点评由F 为Rt △ACB 的重心,因而a 、b 、•c•均能用两条中线长的代数式来表示.•又由CF 2=EF ·BF,问题获解.本题应用方程的思想方法处理平面几何的有关计算问题,其思路清晰,解题步骤规范.中考真题欣赏例1 (2003年南宁市中考题) 已知E 是△ABC 的内心,∠A 的平分线交BC 于点F,且与△ABC 的外接圆相交于点D,如图. (1)求证:∠DBE=∠DEB;(2)若AD=8cm,DF:FA=1:3,求DE 的长.证明 (1)∵E 是△ABC 的内心,∴∠1=∠2,∠3=∠4. ∵∠BED=∠3+∠1,∠5=∠2, ∴∠4+∠5=∠3+∠2=∠3+∠1, 即∠EBD=∠BED;(2)∵∠EBD=∠BED,∴DE=DB.∵∠D=∠D,∠5=∠2=∠1,∴BD 2=AD ·FD.∵DF:FA=1:3,AD=8, ∴FD:AD=1:4,184DF ,∴DF=2(cm). ∴B D 2=8×2=16,∴DE=BD=4(cm).点评利用内心,圆周角等性质将已知和未知关系联系起来,从而使问题获解.例2 (2001年上海市业务数学招生试题)如图,已知O 是△ABC 的边AB 、AC 的中垂线的交点,I 是∠ABC 、∠ACB 的平分线的交点,且∠I+∠BOC=180°.求∠BAC 的度数.解析 ∵O,I 分别是△ABC 的外心和内心,∴∠BOC=2∠BAC,∠I=90°+12∠BAC, 又∵∠I+∠BOC=180°, ∴90°+12∠BAC+2∠BAC=180°. ∴∠BAC=36°. 点评利用外心和内心的性质,将∠BOC 、∠BIC 用∠BAC 来表示,然后建立方程得解.竞赛样题展示例1 (2003年黄冈数学特长生选拔试题)如图,△ABC 中,AB=1998,BC=1999,AC=2000,I 为内心,G 为重心,求IG 的长.解析 连结AI 并延长交BC 于O,连AG 并延长交BC 于J,连BI,IG,由角平分线的性质定理得又∵BO+OC=1999,∴BO=999,OC=1000.又∵BJ=JC=19992,∴OJ=12又∵BI 为角的平分线,∴1998999AB AI BO IO ===2,而AG GJ=2, ∴IG ∥OJ,∴23IG OJ =, GI=23×12=13.点评连结AI,AG 并延长交边BC 于O 、J,连BI.由角平分线的性质可求出BO 、OC 的长,利用角的平分线的性质可计算出AI IO 的值,因为G 为重心,同样可知AG GJ 的值,发现AI IO =AG GJ,从而计算出IG 的长.例2 (第23届加拿大奥赛预选题)△ABC 的外心为O,AB=AC,如图,D 是AB•的中点,E 是△ACD 的重心.证明:OE ⊥CD.证明 设F 、F 分别为AC 、BC 的中点,连结AG 、DF,设AG 交DC 于H,GF 交DC 于I,• 则O 在AG 上,E 在OF 上. ∵AB=AC,AG ⊥BC,DF //12BC. ∴HO ⊥DE,∵D 、F 、G 分别为AB 、AC 和BC 的中点,知H 为△ABC 的重心, ∴DH=13DC=23DI. 由E 为△ADC 的重心,知DE=23DF. 由23DH DEDI DF==,∴EH ∥IF,即EH ∥AB, 由O 为△ABC 的外心,知OD ⊥AB,OD ⊥EH,OH ⊥DE,OD ⊥HE.知O 为△DEH 的垂心.∴EO ⊥DH,即EO ⊥CD. 点评本例综合运用了重心,垂心和外心的概念与性质.全能训练A 卷1.在△ABC 中,∠A 是钝角,O 是垂心,AO=BC,则cos(∠OBC+∠OCB)的值是( )2.设G 为△ABC 的重心,且AG=6,BG=8,CG=10,则△ABC 的面积为( )A.58B.66C.72D.843.在△ABC 中,BC=3,AC=4,BC 和AC 的中线AE,BD 互相垂直,则AB 等于( ).4.如图,△ABC 的三边是a,b,c,它的外心到三边的距离分别为m,n,p,则m:n:p 等于( ) A.111::a b cB.a:b:cC.cosA:cosB:cosCD.sinA:sinB:sinC 5.如图,在锐角△ABC 中,AD ⊥BC,点D 为垂足,DE ⊥AC,点E 为垂足,DF ⊥AB,•F 为垂曲心,O 为△ABC 的外心. 求证:(1)△AEF ∽△ABC; (2)AO ⊥EF.6.如图,直线PQ过△ABC的重心M,P、Q分别内分AB、AC的比值为p、q。

补充：向量与三角形内心、外心、重心、垂心知识的交汇一、四心的概念介绍（1）重心——中线的交点：重心将中线长度分成2：1； （2）垂心——高线的交点：高线与对应边垂直； （3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等； （4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

二、四心与向量的结合（1）证明：⇔=++0OC OB OA O 是ABC ∆的重心.（2）证明：⇔⋅=⋅=⋅OA OC OC OB OB OA O 为ABC ∆的垂心.*（3）设a ,b ,c 是三角形的三条边长，O 是∆ABC 的内心O OC c OB b OA a ⇔=++0为ABC ∆的内心.证明：b AC c AB 、分别为AC AB 、方向上的单位向量，∴bACc AB +平分BAC ∠,(λ=∴AO b AC c AB +)，令c b a bc ++=λ∴cb a bcAO ++=（b AC c AB +) 化简得0)(=++++AC c AB b OA c b a ∴0=++OC c OB b OA a（4==⇔O 为ABC ∆的外心。

典型例题：例1：O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P 满足)(AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（ ）A ．外心B ．内心C ．重心D ．垂心例2：O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P满足AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（ ）A ．外心B ．内心C ．重心D ．垂心例3：O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P满足OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（ ）A ．外心B ．内心C ．重心D ．垂心练习：1．已知ABC ∆三个顶点C B A 、、及平面内一点P ，满足0=++PC PB PA ，若实数λ满足：AP AC AB λ=+，则λ的值为（ ）A ．2B ．3C ．23D ．6 2．若ABC ∆的外接圆的圆心为O ，半径为1，0=++OC OB OA ，则=⋅OB OA ( )A ．21B ．0C ．1D ．21-3．点O 在ABC ∆内部且满足022=++OC OB OA ，则ABC ∆面积与凹四边形ABOC 面积之比是（ ）A ．0B ．23C ．45D ．344．ABC ∆的外接圆的圆心为O ，若OC OB OA OH ++=，则H 是ABC ∆的（ ）A ．垂心B ．内心C ．重心D ．外心5．O 是平面上一定点，C B A 、、是平面上不共线的三个点，若222OB BC OA =+222AB OC CA +=+，则O 是ABC ∆的（ ）A ．垂心B ．内心C ．重心D ．外心6．ABC ∆的外接圆的圆心为O ，两条边上的高的交点为H ，)(OC OB OA m OH ++=，则实数m =7．已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC →|=12 , 则△ABC 为( )A ．三边均不相等的三角形B ．直角三角形C ．等腰非等边三角形D ．等边三角形 8．已知ABC ∆三个顶点C B A 、、，若CA BC CB AB AC AB AB ⋅+⋅+⋅=2，则ABC ∆为（ ）A ．等腰三角形B ．等腰直角三角形C ．直角三角形D ．既非等腰又非直角三角形 9.在△ABC 中，已知向量21||||0||||(==⋅+AC ACAB ABBC AC AC AB AB AC AB 满足与，则△ABC 为（ ） A ．三边均不相等的三角形 B ．直角三角形 C ．等腰非等边三角形D ．等边三角形 10. 在ΔABC 中，O 为中线AM 上的一个动点，若AM=2，则)(OC OB OA +⋅的最小值为 .补充：向量与三角形内心、外心、重心、垂心知识的交汇答案一、四心的概念介绍（1）重心——中线的交点：重心将中线长度分成2：1； （2）垂心——高线的交点：高线与对应边垂直； （3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等； （4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

立体几何中三角形的四心问题一、外心问题（若PA=PB=PC,则O 为三角形ABC 的 外心）例1．设P 是ΔABC 所在平面α外一点，若PA ，PB ，PC 与平面α所成的角都相等，那么P 在平面α内的射影是ΔABC 的( )A.内心B.外心C.垂心D.重心如图所示，作PO ⊥平面α于O ，连OA 、OB 、OC ，那么∠PAO 、∠PBO 、∠PCO 分别是PA 、PB 、PC 与平面α所成的角，且已知它们都相等.∴Rt ΔPAO ≌Rt ΔPBO ≌Rt ΔPCO. ∴OA ＝OB ＝OC ∴应选B.例2． Rt △ABC 中，∠C ＝９０°，BC ＝３６，若平面ABC 外一点P 与平面A ，B ，C 三点等距离，且P 到平面ABC 的距离为８０，M 为AC 的中点．（１）求证：PM ⊥AC ；（２）求P 到直线AC 的距离；（３）求PM 与平面ABC 所成角的正切值．解析：点P 到△ABC 的三个顶点等距离，则P 在平面ABC 内的射影为△ABC 的外心，而△ABC 为直角三角形，其外心为斜边的中点．证明 （１）∵PA ＝PC ，M 是AC 中点，∴PM ⊥AC解 （２）∵BC ＝３６，∴MH ＝１８，又PH ＝８０，∴PM ＝8218802222=+=+MH PH ，即P 到直线AC 的距离为８２； （３）∵PM=PB=PC ，∴P 在平面ABC 内的射线为△ABC 的外心，∵∠C=90° ∴P 在平面ABC 内的射线为AB 的中点H 。

∵PH ⊥平面ABC ，∴HM 为PM 在平面ABC 上的射影，则∠PMH 为PM 与平面ABC 所成的角，∴tan ∠PMH ＝9401880==MH PH 例3．斜三棱柱ABC —A 1B 1C 1的底面△ABC 中，AB=AC=10，BC=12，A 1到A 、B 、C 三点的距离都相等，且AA1=13，求斜三棱柱的侧面积。

解析：∵A 1A=A 1B=A 1C∴ 点A 1在平面ABC 上的射影为△ABC 的外心，在∠BAC 平分线AD 上 ∵ AB=AC ∴ AD ⊥BC∵ AD 为A 1A 在平面ABC 上的射影∴ BC ⊥AA 1 ∴ BC ⊥BB 1∴ BB 1C 1C 为矩形，S=BB 1×BC=156取AB 中点E ，连A 1E∵ A 1A=A 1B ∴ A 1E ⊥AB∴ 12)2AB (AA E A 2211=-= ∴ 1111120AA C C AA B B S S ==∴ S 侧=396二、内心问题（若P 点到三边AB,BC,CA 的距离相等，则O 是三角形ABC 的 内心）例4．如果三棱锥S —ABC 的底面是不等边三角形，侧面与底面所成的角都相等，且顶点S 在底面的射影O 在ΔABC 内，那么O 是ΔABC 的( )A.垂心B.重心C.外心D.内心解 (1)利用三垂线定理和三角形全等可证明O 到ΔABC 的三边的距离相等，因而O 是ΔABC 的内心，因此选D.说明三角形的内心、外心、垂心、旁心、重心，它们的定义和性质必须掌握.质找出与平面平行的直线。