三角形的三线四心及口诀资料讲解

高中数学三角形四心如何归纳梳
理
高中数学三角形四心（重心垂心外心内心）如何归纳梳理？ -
其实任何事物命名时，通常都有其独特的意图，三角形的心、心、重心也不例外。

用心感受它们的字面意思，你就能区分它们:
1、垂心：因为有“垂”字，要记住是垂线的交点，即三角形高的交点。

2、外心：因为有“外”字，要记住是三角形外接圆的圆心。

由于三角形的三个顶点均在外接圆上，因而连接圆心和三个顶点，分别构成了三个三角形，并且这三个三角形均为等腰三角形。

根据等腰三角形的性质，底上的高为底边的垂直平分线。

因而不难看出，这里外接圆的圆心，即“外心”便是原三角形各边垂直平分线的交点。

3、内心：因为有“内”字，要记住是三角形内切圆的圆心。

由这个内切圆的圆心向各对边做垂线，再连接该圆心与三角形的三个顶点，由切线长定理和三角形全等，易得圆心与三角形三个顶点的连线，分别平分了三角形的三个内角。

因而不难看出，这里的内切圆圆心，即“内心”便是原三角形各角平分线的交点。

4.重心:对于形状规则的物体，重心通常是其几何中心，也可以说是对称中心。

从三角形三条中线相交形成的交点开始，连接三角形三个顶点形成的三个三角形面积相等。

换句话说，这
个交点就是它的几何中心，也就是重心。

需要注意的是，几何中心只是形状规则、密度均匀的物体的重心。

三角形的“四心”所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

三角形的“四心”是初中三角形的重难点，也与高中向量、三角函数等知识联系甚紧，需要认真学懂。

一、三角形的外心定义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC 的重心一般用字母O 表示。

性质：1、外心到三顶点等距，即OC OB OA 。

2、外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ,,. 3、AOB C AOC B BOC A 21,21,21。

二、三角形的内心定义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC 的内心一般用字母I 表示，它具有如下性质：性质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝21三角形的周长内切圆的半径．3.CE CD BD BF AF AE ,,；CD BF AE 三角形的周长的一半。

4.,2190A BIC B CIA 2190，C AIB 2190。

三、三角形的垂心定义：三角形三条高的交点叫垂心。

ABC 的垂心一般用字母H 表示。

性质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ,,。

2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B 。

四、三角形的“重心”：定义：三角形三条中线的交点叫重心。

ABC 的重心一般用字母G 表示。

性质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GFGC GE GB GD GA 2,2,23.重心的坐标是三顶点坐标的平均值．即3,3C B A G C B A G y y y y x x x x .4.ABC AGB CGA BGC S S S S 31。

初中数学知识点：三角形的内心、外心、中心、重心三角形的四心定义：1、内心：三角形三条内角平分线的交点，即内切圆的圆心。

内心是三角形角平分线交点的原理：经圆外一点作圆的两条切线，这一点与圆心的连线平分两条切线的夹角(原理：角平分线上点到角两边距离相等)。

2、外心：是三角形三条边的垂直平分线的交点，即外接圆的圆心。

外心定理：三角形的三边的垂直平分线交于一点。

该点叫做三角形的外心。

3、中心：三角形只有五种心重心、垂心、内心、外心、旁心，当且仅当三角形是正三角形的时候，四心合一心，称做正三角形的中心。

4、重心：重心是三角形三边中线的交点。

三角形的外心的性质：1.三角形三条边的垂直平分线的交于一点，该点即为三角形外接圆的圆心;2三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合;3.锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合。

在△ABC中4.OA=OB=OC=R5.∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA6.S△ABC=abc/4R三角形的内心的性质：1.三角形的三条角平分线交于一点，该点即为三角形的内心2.三角形的内心到三边的距离相等，都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中，∠C=90°，r=(a+b-c)/2.5.∠BOC = 90 °+∠A/2 ∠BOA = 90°+∠C/2 ∠AOC = 90 °+∠B/26.S△=[(a+b+c)r]/2 (r是内切圆半径)三角形的垂心的性质:1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。

图3图4三角形的“四心”三角形是最重要的基本平面图形，很多较复杂的图形问题可以化归为三角形的问题.如图1 ，在三角形△ABC 中，有三条边,,AB BC CA ，三个顶点,,A B C ，在三角形中，角平分线、中线、高（如图2）是三角形中的三种重要线段.一、三角形的重心三角形的三条中线相交于一点，这个交点称为三角形的重心. 1、三角形的三条中线必交于一点1.已知：如图3中△ABC 的两条中线AD 、BE 相交于点O ，连结并延长CO ，交AB 于点F 。

求证：AF=CF证明：延长OF 到点G ，使OG=OC ∵OG=OC, ∴点O 是CG 的中点又∵点D 是BC 的中点 ∴OD 是△BGC 的一条中位线 ∴AD ∥BG ∵点O 是CG 的中点，点E 是AC 的中点 ∴OE 是△CGA 的一条中位线 ∴BE ∥AG∵AD ∥BG ，BE ∥AG ,∴四边形AOBG 是平行四边形 ∴AB 、OG 互相平分,∴AF=CF2、三角形重心的性质(1).重心到顶点的距离与重心到对边中点的距离之比为2：1。

(2).重心和三角形3个顶点组成的3个三角形面积相等。

例1：如图4中，已知三角形的一边和重心，你能找到三角形的第三个顶点吗?请你画出它的位置。

图1图2图5图6三角形的三条高线相交于一点，这个交点称为三角形的垂心. 1、三角形的三条高必交于一点已知：如图5中△ABC 中，AD 、BE 是两条高，AD 、BE 交于点O ，连接CO 并延长交AB 于点F 求证：CF ⊥AB证明：连接DE ∵∠ADB=∠AEB=90°,且在AB 同旁，∴A 、B 、D 、E 四点共圆 ∴∠ADE=∠ABE （同弧上的圆周角相等） ∵∠EAO=∠DAC,∠AEO=∠ADC=90°∴△AEO ∽△ADC ∴AE/AD=AO/AC 即AE/AO=AD/AC ∴ΔEAD ∽ΔOAC ∴∠ACF=∠ADE=∠ABE 又∵∠ABE+∠BAC=90° ∴∠ACF+∠BAC=90° ∴CF ⊥AB2、三角形垂心的性质(1).锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外(2).△ABC 中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AO·OD=BO ·OE=CO ·OF例2：如图6，点H 是等腰△ABC 的垂心，在底边BC 长度不变的情况下，顶点A 到底边BC 的距离变化时，乘积HBC ABC S S ∆∆⋅的值是否变化？证明你的结论.图7图8图9三角形的三条内角平分线相交于一点，这个交点称为三角形的内心. 1、三角形的三条内角平分线必交于一点己知：如图7，在△ABC 中，∠A 与∠B 的角平分线交于点O ，连接OC求证：OC 平分∠ACB 证明：过O 点作OD,OE,OF 分别垂直于BC,AC,AB,垂足分别为D,E,F∵AO 平分∠BAC,∴OE=OF ；∵BO 平分∠ABC,∴OD=OF ；∴OD=OE ∴O 在∠ACB 角平分线上 ∴CO 平分∠ACB2、三角形内心的性质(1).三角形的内心到三边的距离相等，都等于三角形的内切圆半径r ，cb a S r ABC++=∆2(2).在Rt △ABC 中，∠C=90°，2cb a r -+=． (3).∠BOC = 90 °+∠A/2， ∠BOA = 90 °+∠C/2， ∠AOC = 90 °+∠B/2例3：已知：如图8，在△ABC 中，∠C=90°，∠A 和∠B 的平分线相交于P 点，PE ⊥AB 于E 点，BC=3，AC=4，求BE AE ⋅的值.例4：已知：如图9，△ABC 三边长分别为,,BC a AC b AB c ===，I 为△ABC 的内心，且I 在△ABC 的边B C A CA B 、、上的射影分别为D E F 、、，求证：2b c aAE AF +-==.图10四、三角形的外心三角形三边的垂直平分线相交于一点，这个交点称为三角形的外心.1、三角形的三边垂直平分线必交于一点已知：如图10，在△ABC 中，AB,AC 的垂直平分线DO,EO 相交于点O求证：O 点在BC 的垂直平分线上证明：连结AO,BO,CO ，∵DO 垂直平分AB ，∴AO=BO ∵EO 垂直平分AC ，∴AO=CO∴BO=CO 即O 点在BC 的垂直平分线上2、三角形外心的性质(1).三角形的外心到三个顶点的距离相等，都等于三角形的外接圆半径R ，即OA=OB=OC=R; (2).锐角三角形的外心在三角形内；钝角三角形的外心在三角形外；直角三角形的外心与斜边的中点重合;(3).∠BOC=2∠BAC ，∠AOB=2∠ACB ，∠COA=2∠CBA.例5：已知：△ABC 中，AB=AC=13，BC=10. 求：（1）△ABC 内切圆的半径r ； （2）△ABC 外接圆的半径R.例6：已知△ABC 的重心和内心为同点O ，求证：△ABC 为正三角形.图11 练习1.若想在一块质地均匀的三角形木板上穿一根线，使它水平地悬在空中，则穿线的位置应该是三角形木板的（ ）A. 垂心B. 重心C. 内心D. 外心2.如图11，D 是△ABC 的边BC 上的上点，点E 、F 分别是△ABD 和△ACD 的重心，连结EF 交AD 于点G ，则GADG___________.3.若三角形的垂心和重心重合，求证：该三角形为正三角形.4． （1） 若三角形ABC 的面积为S ，且三边长分别为a b c 、、，则三角形的内切圆的半径是___________;（2）若直角三角形的三边长分别为a b c 、、（其中c 为斜边长），则三角形的内切圆的半径是___________. 并请说明理由.5.求证：三角形的任一顶点到垂心的距离，等于外心到对边的距离的二倍．。

A
O
A
O
B
C
B
C
二、垂心 三角形三边上的高交于一点，这一点叫三角形的垂心 垂心。 三角形三边上的高交于一点，这一点叫三角形的垂心。
C′ F
AE DBiblioteka B′证明垂心定理B
A′
证明: 三条高， 证明 AD、BE、CF为∆ABC三条高， 、 、 为 三条高 过点A、 、 分别作对边的平行线 过点 、B、C分别作对边的平行线 相交成∆A′B′C′，AD为B′C′ 相交成 ， 为 的中垂线；同理BE、 也分别为 的中垂线；同理 、CF也分别为 C A′C′、A′B′的中垂线， 的中垂线， 、 的中垂线 由外心定理，它们交于一点， 由外心定理，它们交于一点， 命题得证． 命题得证．
F G B D C E
重心
四、内心
三角形三内角平分线交于一点，这一点为三角形内切圆的圆心，称内心。 三角形三内角平分线交于一点，这一点为三角形内切圆的圆心， 内心。
证明内心定理
的平分线相交于I, 证明 : 设∠A、∠C的平分线相交于I, ID⊥BC，IE⊥AC， 过I作ID⊥BC，IE⊥AC， IF⊥AB，则有IE=IF=ID IE=IF=ID． IF⊥AB，则有IE=IF=ID． A 因此I也在∠ 的平分线上， 因此I也在∠C的平分线上， 即三角形三内角平分线 交于一点． 交于一点． I
三角形的“四心” 三角形的“四心”
一、 外心
三角形三边的中垂线交于一点，这一点为三角形外接圆的圆心， 外心。 三角形三边的中垂线交于一点，这一点为三角形外接圆的圆心，称外心。
证明外心定理
证明: 设AB、BC的中垂线交于点 ， 的中垂线交于点O， 证明 、 的中垂线交于点 则有OA=OB=OC， 则有 ， 也在AC的中垂线上 故O也在 的中垂线上， 也在 的中垂线上， 因为O到三顶点的距离相等 到三顶点的距离相等， 因为 到三顶点的距离相等， 故点O是∆ABC外接圆的圆心． 故点 是 外接圆的圆心． 外接圆的圆心 因而称为外心． 因而称为外心．

三角形“四心”定义与性质 所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定 义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性 质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,.3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。

二、三角形的内心定 义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示，它具有如下性质：性 质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3.CE CD BD BF AF AE ===,,；=++CD BF AE 三角形的周长的一半。

4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ，C AIB ∠+=∠2190 。

三、三角形的垂心定 义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性 质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B 。

四、三角形的“重心”：定 义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性 质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值． 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质：（1）0=++GC GB GA ；（2）)(31PC PB PA PG ++=，5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。

三角形“四心”定义与性质-CAL-FENGHAI.-(YICAI)-Company One1三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定 义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性 质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。

二、三角形的内心 定 义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示，它具有如下性质：性 质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3.CE CD BD BF AF AE ===,,；=++CD BF AE 三角形的周长的一半。

4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ，C AIB ∠+=∠2190 。

三、三角形的垂心定 义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性 质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B 。

四、三角形的“重心”：定 义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性 质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值． 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质：（1）0=++GC GB GA ；（2）)(31++=，5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。

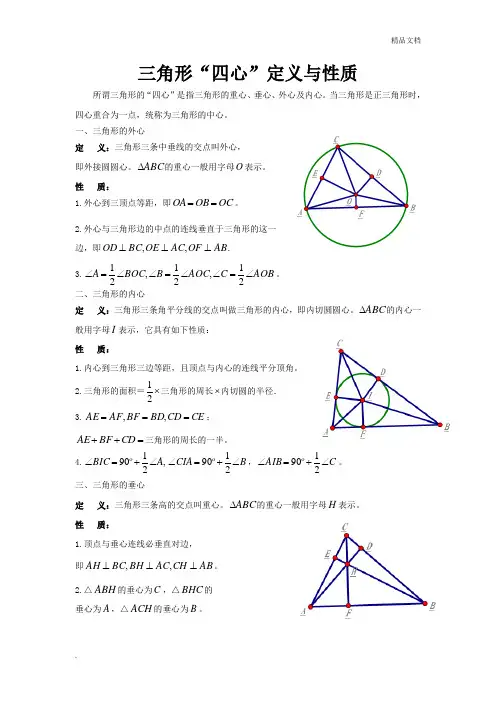
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定 义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性 质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。

二、三角形的内心定 义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示，它具有如下性质：性 质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3.CE CD BD BF AF AE ===,,；=++CD BF AE 三角形的周长的一半。

4.,2190A BIC ∠+=∠οB CIA ∠+=∠2190ο，C AIB ∠+=∠2190ο。

三、三角形的垂心定 义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性 质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B 。

四、三角形的“重心”：定 义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性 质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值． 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质：（1）0=++GC GB GA ；（2）)(31PC PB PA PG ++=，5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。

三角形的三线、四心及口诀内心是三条角平分线的交点，它到三边的距离相等。

外心是三条边垂直平分线的交点，它到三个顶点的距离相等。

（是充要条件）重心是三条中线的交点，它到顶点的距离是它到对边中点距离的2 倍。

垂心是三条高的交点，它能构成很多直角三角形相似。

旁心是一个内角平分线与其不相邻的两个外角平分线的交点，它到三边的距离相等。

重心
三条中线定相交，交点位置真奇巧, 重心分
割中线段，数段之比听分晓, 垂心三角形上作三高，三高必于垂心交, 直角三角形有十二，构成六对相似形内心三角对应三顶点，角角都有平分线，点至三边均等距，可作三角形内切圆，外心三角形有六元素，三个内角有三边, 此点定义为外心，用它可
作外接圆,
交点命名为重心，重心性质要明了，
长短之比二比一，灵活运用掌握好。

高线分割三角形，出现直角三对整，
四点共圆图中有，细心分析可找清。

三线相交定共点，叫做内心有根源，
此圆圆心称内心，如此定义理当然。

作三边的中垂线，三线相交共一点，
内心、外心莫记混，内切、外接是关键。

分别化出锐角、直角、钝角三角形的三线、四心重心... 中线交点... 3 个定点的坐标为(x1,y1) (x2,y2) (x3,y3) 重心坐标就是(x1+x2+x3/3,y1+y2+y3/3)
第五个心：旁心
三角形的旁切圆（与三角形的一边和其他两边的延长线相切的圆）的圆心叫做旁心。

旁心是一个三角形内角平分线与其不相邻的两个外角平分线的交点，它到三角形三边的距离相等。

一个三角形有三个旁心，而且一定在三角形外。

只供学习与交流。

2、垂心：三角形三条高线的交点叫垂心．它与顶点的连线 垂直于对边．
在向量表达形式中，若H是△ABC的垂心，则
3、内心：三角形三条内角平分线的交点叫内心．内心就是三角形内 切圆的圆心，它到三角形三边的距离相等．
在向量表达形式中，若点I是△ABC的内心，则有
ห้องสมุดไป่ตู้
A E
B
D
C
4、外心：三角形三条边的中垂线的交点叫外心．外心就是三角形 外接圆的圆心，它到三角形的三个顶点的距离相等．
三角形“四心”的概念与性质
1、重心：三角形三条中线的交点叫重心．它到三角形顶点距离与该点到 对边中点距离之比为2∶1.
（1）在向量表达形式中，设点G是△ABC所在平面内的一点，则当点G是 △ABC的重心时，
（2）在向量的坐标表示中，若G，A，B，C分别是三角形的重心和三 个顶点，且分别为G(x，y)，A(x1，y1)，B(x2，y2)，C(x3，y3)，
AB CA
BA CB
CA BC
则O为三角形ABC的 心.
（3）设点O在三角形ABC的内部，且
OA 2OB 3OC 0, 则 SABC : SAOC
.
在向量表达形式中，若点O是△ABC的外心，则
例6 （1）若点O为三角形ABC所在平面内的 一定点，P是面ABC呢一动点，若
(PB PC) (OB OC) (PC PA) (OA OC) 0
则O为三角形ABC的 心.
（2）三个不共线的向量OA,OB,OC 满足
OA ( AB CA ) OB ( BA CB ) OC ( CA BC ) 0,

三角形“四心”定义与性质 所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定 义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性 质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,.3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。

二、三角形的内心定 义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示，它具有如下性质：性 质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3.CE CD BD BF AF AE ===,,；=++CD BF AE 三角形的周长的一半。

4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ，C AIB ∠+=∠2190 。

三、三角形的垂心定 义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性 质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B 。

四、三角形的“重心”：定 义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性 质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值． 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质：（1）0=++GC GB GA ；（2）)(31PC PB PA PG ++=，5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。

三角形“四心”定义与性质 所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定 义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性 质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,.3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。

二、三角形的内心定 义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示，它具有如下性质：性 质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3.CE CD BD BF AF AE ===,,；=++CD BF AE 三角形的周长的一半。

4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ，C AIB ∠+=∠2190 。

三、三角形的垂心定 义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性 质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B 。

四、三角形的“重心”：定 义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性 质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值． 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质：（1）0=++GC GB GA ；（2）)(31PC PB PA PG ++=，5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。

三角形“四心〞定义与性质所谓三角形的“四心〞是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定 义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性 质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。

二、三角形的内心定 义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示，它具有如下性质：性 质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3.CE CD BD BF AF AE ===,,；=++CD BF AE 三角形的周长的一半。

4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ，C AIB ∠+=∠2190 。

三、三角形的垂心定 义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性 质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B 。

四、三角形的“重心〞：定 义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性 质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值． 即3,3C B A G C B A G y y y y x x x x ++=++=. 4.向量性质：〔1〕0=++GC GB GA ；〔2〕)(31PC PB PA PG ++=，5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。

三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点,统称为三角形的中心.一、三角形的外心定 义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性 质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,.3。

AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。

二、三角形的内心 定 义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质：1。

内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3。

CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半.4。

,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 . 三、三角形的垂心定 义:三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性 质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,.2.△ABH 的垂心为C ，△BHC 的垂心为A ，△ACH 的垂心为B .四、三角形的“重心”：定 义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性 质:1。

顶点与重心G 的连线必平分对边。

2。

重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值． 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质：（1)0=++GC GB GA ；（2）)(31PC PB PA PG ++=，5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。

Aቤተ መጻሕፍቲ ባይዱ
性质：(1) 重心到顶点的距离与到对边 中点的距离之比为2:1
(2) 重心的坐标是三个顶点的坐 标的算术平均数
(3) 以重心为起点，以三顶点为 终点的三个向量之和等于零 向量
F G
E
B
D
C
AG BG CG 2 GD GE GF
G( xA xB xC , yA yB yC )
3
3
GA GB GC 0
注注 意意
1、三角形的中心：
只有正三角形才有中心，这时重心，内心，外心，垂心，四心合一。
2、旁心
三角形的旁切圆（与三角形的一边和其他两边的延长线相切的圆） 的圆心，叫做三角形的旁心，三角形有三个旁心，都在三角形外，旁心 到三边的距离相等。
3、本文所述性质皆为常用性质，并不全面。
欢迎批评指正！谢谢！
定理：三角形的三条高线必交于一点，这个点叫做三角形 的垂心 如图，H为△ABC的垂心
性质：(1) 垂心与顶点的连线垂直于对边 (2) 垂心分每条高的两部 分乘积相等 AH⊥BC，BH ⊥ AC,CH ⊥ AB
二四、、内重心心
定理：三角形的三边中线必交于一点，这个点叫做三角形
的重心
如图，G为△ABC的重心
三角形的“四心”及简单性质
By 郯城美澳数学QQ群 群号：454463883
二一、、内外心心
定理：三角形三条边的垂直平分线必交于一点，这个点是三角
形的外接圆的圆心，简称外心
A
如图，O为△ABC的外心
性质：(1) 外心到三个顶点的距离相等 (2) 锐角△的外心在三角形的内部 直角△的外心在斜边的中点处 钝角△的外心在三角形的外部
O C
B
OA=OB=OC

三角形的心三角形只有五种心重心:三中线的交点,三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍；垂心:三高的交点;内心:三内角平分线的交点,是三角形的内切圆的圆心的简称;外心:三中垂线的交点;旁心:一条内角平分线与其它二外角平分线的交点.(共有三个.)是三角形的旁切圆的圆心的简称.当且仅当三角形是正三角形的时候,四心合一心,称做正三角形的中心.1三角形重心重心是三角形三边中线的交点，三线交一可用燕尾定理证明，十分简单。

证明过程又是塞瓦定理的特例。

已知：△ABC中，D为BC中点，E为AC中点，AD与BE交于O，CO延长线交AB于F。

求证：F为AB中点。

证明：根据燕尾定理，S△AOB=S△AOC，又S△AOB=S△BOC，∴S△AOC= S△BOC，再应用燕尾定理即得AF=BF，命题得证。

重心的几条性质：1、重心到顶点的距离与重心到对边中点的距离之比为2：1。

2、重心和三角形3个顶点组成的3个三角形面积相等。

3、重心到三角形3个顶点距离的平方和最小。

4、在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，即其坐标为((X1+ X2+X3)/3,(Y1+Y2+Y3)/3)；空间直角坐标系——横坐标：(X1+X2+X3)/3 纵坐标：(Y 1+Y2+Y3)/3 竖坐标：（z1+z2+z3）/35、三角形内到三边距离之积最大的点。

重心三条中线定相交，交点位置真奇巧，交点命名为“重心”，重心性质要明了，重心分割中线段，数段之比听分晓；长短之比二比一，灵活运用掌握好．2三角形垂心的性质设⊿ABC的三条高为AD、BE、CF，其中D、E、F为垂足，垂心为H，角A、B、C的对边分别为a、b、c，p=(a+b+c)/2．1、锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外.2、三角形的垂心是它垂足三角形的内心；或者说，三角形的内心是它旁心三角形的垂心；3、垂心H关于三边的对称点，均在△ABC的外接圆上。

技法点拨试题#究谈"#形％‘‘四（”陶爱萍在向量的教学中，经常会根据已知条件判断动 点是三角形的什么“心”。

下面先介绍“四心”，并讲解 相应例题，让学生对这一难点问题有所突破。

1.重心:三角形三条中线的交点。

如果"，#，$分别是A%&C三边的中点，贝l4M，&#，C(必交于一点 G，此点即为A%*C的重心，且满足+G#GM=&G#G#= CG#G(=2 #1(这由中位线定理容易证得)$并且有这个结论：A+&C中，G满足$+$+$!&[0，+$).则动点2经过A/&C的重心。

2.垂心:三角形三条高线的交点。

例2# A/&C中，0点满足0/ •0&=0&•0'=0'•0A。

=0贝吣点为AA&C的垂心。

3. 外心:三角形三条边的中垂线的交点，因为它到三个顶点的距离相等，所以它又是三角形的外接圆的圆心。

例3 #AA&C中，A&2-/C2.2/0-C&贝U动点0经过AA&C的外心。

4. 内心:三角形三个内角平分线的交点，因为它到三角形三条边的距离相等，所以它又是三角形内切圆的圆心。

例4# AA&C中，动点2满足02=0/+!| '+菩(\AB\IACI I!&[0，+$)则2的轨迹经过AA&C的内心。

注意:向量加法的平行四边形法则，是两个不共线的向量起点相同时，做出平行四边形c两个不共线向量的和，但往往取中点利用A&+AC=2#^(袁中"为A&的中点)M有利于问题的解决。

总之，以上各题要求学生善于观察所给式子的特点，灵活变形，化为能看出结论的形式。

(作者单位：安徽省南陵中学）贝忆为AA&C的重心，反之也成立。

证明:1先取A&白'中；"，则 G A+G&+GC=2)"+GC=0...GC=-2GM.•.GC//GM"G在中线C"上且满足\GC\=2\G"\•G为AA&C的重心。