定积分的分步积分法.
- 格式:ppt
- 大小:95.00 KB
- 文档页数:4
定积分的分部积分法经典例题
定积分的应用一般出现在综合题的最后一题,题型仅有两种:第一,求曲线围成的面积;第二求旋转体体积(绕x轴旋转,绕y轴旋转)。
1.求面积
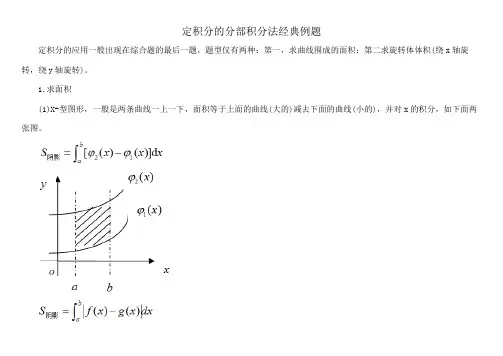
(1)X-型图形,一般是两条曲线一上一下,面积等于上面的曲线(大的)减去下面的曲线(小的),并对x的积分,如下面两张图。
求面积首要问题是画出草图,图形的上下位置(或者左右位置),交点一定要做得准确。
通常曲线,例直线、抛物线、双曲线、指数、对数、三角函数的图像要画得熟练、准确。
求出结果后要检验,这样的题型是一个实际问题,所得结果要合乎逻辑。
(2)Y-型,一般是两条曲线一左一右,面积等于右边的曲线(大的)减去左边的曲线(小的),并对y的积分,如下图
2.旋转体体积
求旋转体体积时要充分发挥几何空间想象能力,要想象出旋转出的体积大概是什么形状的。
(1)X-型图形
绕x轴旋转所得图形的体积
绕y轴旋转所得图形的体积
(2)Y-型图形
绕x轴旋转所得图形的体积
绕y轴旋转所得图形的体积
常考题型如下:。

定积分可以用分部积分法定积分是高中数学中非常重要的一个概念,同时也是微积分的基础。
在计算定积分的时候,我们可以采用分部积分法,这是一种非常有效的方法。
分部积分法首先要明确一个概念,即积分中的两个因子是具有不同的特点的。
我们把这两个因子分别称为“被积函数”和“微分形式”。
在使用分部积分法求解定积分的时候,我们需要根据被积函数和微分形式的特点,合理地选取分别代表它们的函数。
通常情况下,我们可以选取被积函数为u,微分形式为dv,然后利用以下公式进行计算:∫u dv = uv - ∫v du公式中的u代表被积函数,v代表微分形式。
通过运用分部积分公式,我们可以快速、准确地求出定积分。
当然,作为一种高级的数学方法,分部积分法需要我们掌握一些具体的技巧和方法。
首先,我们需要选取一个合适的u和dv,使得∫u dv的求解变得容易或具有明显的规律。
在选择u和dv的时候,我们需要考虑它们的微分形式的次数、变化规律、奇偶性等方面的属性,并且需要经过反复尝试才能选出最佳的组合。
其次,我们需要注意确定分部积分过程中的边界条件。
在确定边界条件时,我们要考虑清楚被积函数和微分形式的取值范围,并且要注意积分上限和下限的影响。
最后,我们还需要注意分部积分法的运用场景。
分部积分法适用于一些特定的被积函数和微分形式,例如多项式函数、三角函数、指数函数等,但是对于某些函数,分部积分法可能并不适用。
因此,在运用分部积分法的时候,我们需要考虑被积函数的具体性质,合理地选择不同的求解方法。
总之,分部积分法是高中数学中非常重要且实用的求解定积分的方法,掌握了这个方法,能够让我们在求解数学题目和解决实际问题时更加得心应手。
为了从根本上提高分部积分的运用能力,我们需要多思考、多实践,不断提高自己的数学素养和技巧水平。

§6.5 定积分的分部积分法因为vdu udv uv d +=)(,两边从a 到b 取定积分有:⎰⎰⎰+==b abab ab avdu udv uv uv d ][)(,所以 ⎰⎰-=bab a ba vdu uv udv ][ 例1⎰⎰⎰-=-=5151515151]ln [ln ])[(ln ln dx xx x x x xd x x xdx 45ln 5][05ln 551-=--x例2 11|][1110110=+-=-=-==⎰⎰⎰xx xxx x x e e e e dxe xe xde dx xe例3211|c o s 0s i n|s i n s i n c o s 0000-=--=+=-==⎰⎰⎰πππππx dx x x x x xd xdx x例4⎰⎰⎰-==ee e e xd x x x x xd xdx x 1121221ln 21]ln [21)2(ln ln=414|212122122122122+=⋅-=-⎰e x e dx x x e e e例5⎰⎰=2ln 0222ln 032221dx e x dx e x x x 令2x t =,则原式=⎰⎰⎰-==2ln 02ln 02ln 02ln 021][212121dt e te tde dt te tt t t =212ln 212212ln |212)2(ln 212ln 0-=+⋅-=-⋅t e 例6 求⎰⎰=2020c o s c o s ππx xx d e xd xe =dx x e x d e e x x xx⎰⎰+-=-⋅202020sin 1cos |cos πππ=⎰⎰-⋅+-=+-202020sin ])[(sin 1sin 1πππx d e e x xde x xx=xdx e e x cos 1202⎰-+-ππ∴ 1cos 2220-=⎰ππe xdx e x∴ ⎰-=202)1(21cos ππe x e x例7⎰342s i n ππdx xx=⎰⎰+-=-343434cot ]cot [cot ππππππxdx x x x xd=++-=⎰dx x x 34sin cos 493ππππ⎰++-=34sin sin 493ππππx xd 34]sin [ln 493ππππx ++-=23ln 21493++-ππ 利用定积分还可以求某些和的近似值。







分部积分计算方法
分部积分法是一种微积分运算方法,主要用于计算定积分。
它的基本思想是将一个积分式子拆分成两个部分,然后对其中一个部分求导,对另一个部分求积分,从而将原来的积分问题转化为求导和积分的组合问题。
分部积分的原理可以用以下公式表示:
∫u(x)v'(x)dx = u(x)v(x) - ∫v(x)u'(x)dx
其中,u(x)和v(x)是可导的函数,u'(x)和v'(x)是它们的导数。
分部积分的应用:
1. 计算定积分:通过分部积分,可以将原本复杂的定积分问题转化为求导和积分的组合问题,从而简化计算过程。
例如,计算∫xsin(x)dx,可以选择
u(x) = x,v'(x) = sin(x),然后按照分部积分公式进行计算。
2. 解决微分方程:分部积分法可以用于求解某些微分方程。
例如,对于形如f'(x)g(x) + f(x)g'(x)的微分方程,可以通过分部积分法将其转化为更容易求解的形式。
分部积分的步骤:
1. 确定被积函数:首先确定要求积分的函数。
2. 选择适当的u和v:根据被积函数的特性,选择适当的u和v,使得求导和求积分的过程更加简便。
3. 应用分部积分公式:将选择的u和v代入分部积分公式,进行计算。
4. 反复应用:如果需要继续对其他部分进行分部积分,可以将上一步的结果代入下一步中进行计算。
通过分部积分法,可以将一些难以直接计算的定积分转化为容易计算的形式,从而简化计算过程。
但需要注意的是,在选择u和v时,应确保选择合适,否则可能会导致计算过程更加复杂。

分部积分法定积分公式一、分部积分法基本原理。
1. 不定积分中的分部积分法公式。
- 设u = u(x),v = v(x)具有连续导数,则∫ udv=uv - ∫ vdu。
- 推导:由(uv)^′ = u^′ v+uv^′,移项可得uv^′=(uv)^′ - u^′ v。
- 对等式两边求不定积分,∫ uv^′dx=∫(uv)^′dx-∫ u^′ vdx,即∫ udv = uv-∫ vdu。
2. 定积分中的分部积分法公式。
- 设u = u(x),v = v(x)在[a,b]上具有连续导数,则∫_a^budv=<=ft.uvright_a^b-∫_a^bvdu。
- 推导:由不定积分的分部积分公式∫ udv = uv-∫ vdu,对等式两边在[a,b]上求定积分。
- 即∫_a^budv=<=ft[∫ udv]_a^b=<=ft[uv - ∫ vdu]_a^b=<=ft.uvright_a^b-∫_a^bvdu,其中<=ft.uvright_a^b=u(b)v(b)-u(a)v(a)。
1. 示例一:计算∫_0^πxsin xdx- 设u = x,dv=sin xdx。
- 则du=dx,v =-cos x(因为∫sin xdx =-cos x + C)。
- 根据定积分的分部积分公式∫_0^πxsin xdx=<=ft.-xcos xright_0^π-∫_0^π-cos xdx。
- 先计算<=ft.-xcos xright_0^π=-πcosπ - 0×cos0=π。
- 再计算∫_0^π-cos xdx=-<=ft.sin xright_0^π=0。
- 所以∫_0^πxsin xdx=π。
2. 示例二:计算∫_1^eln xdx- 设u=ln x,dv=dx。
- 则du=(1)/(x)dx,v = x。
- 由定积分的分部积分公式∫_1^eln xdx=<=ft.xln xright_1^e-∫_1^ex×(1)/(x)dx。