实验四异方差性13金数2班201330110203何健华教材
- 格式:docx
- 大小:531.10 KB
- 文档页数:10

异方差性实验报告篇一:计量经济学上机实验报告(异方差性)提示:打包保存时自己的文件夹以“学号姓名”为文件夹名,打包时文件夹内容包括:本实验报告、EViews工作文件。
篇二:Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理,以及相关的Eviews操作方法。
【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据,练习检查和克服模型的异方差的操作方法。
【4-16】表4-1给出了美国18个行业1988年研究开发(R&D)费用支出Y与销售收入X的数据。
请用帕克(Park)检验、戈里瑟(Gleiser)检验、G-Q检验与怀特(White)检验来检验Y关于X的回归模型是否存在异方差性?若存在【实验步骤】一检查模型是否存在异方差性1、图形分析检验(1)散点相关图分析做出销售收入X与研究开发费用Y的散点相关图(SCATX Y)。
观察相关图可以看出,随着销售收入的增加,研究开发费用的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
(2)残差图分析首先对数据按照解释变量X由小至大进行排序(SORT X),然后建立一元线性回归方程(LS Y C X)。
因此,模型估计式为: Y?187.507?0.032*X ----------(*) ?(0.17)(2.88) R2=建立残差关于X的散点图,可以发现随着X增加,残差呈现明显的扩大趋势,表明存在递增的异方差。
2、Park检验建立回归模型(LS Y C X),结果如(*)式。
生成新变量序列: GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型(LS LNE2 C LNX)。
从下图所示的回归结果中可以看出,LNX的系数估计值不为0且能通过显著性检验,即随机误差项的方差与解释变量存在较强的相关关系,即认为存在异方差性。
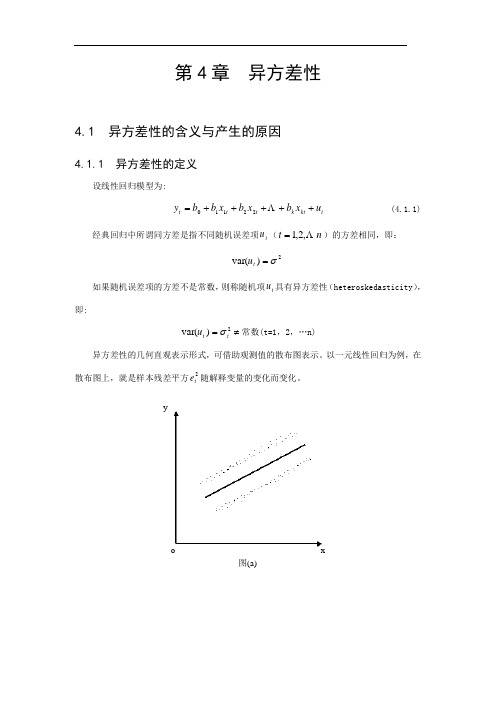
第4章 异方差性4.1 异方差性的含义与产生的原因4.1.1 异方差性的定义设线性回归模型为:t kt k t t t u x b x b x b b y +++++= 22110 (4.1.1)经典回归中所谓同方差是指不同随机误差项t u (n t ,2,1=)的方差相同,即:2)var(σ=t u如果随机误差项的方差不是常数,则称随机项t u 具有异方差性(heteroskedasticity ),即:2)var(t t u σ=≠常数(t=1,2,…n)异方差性的几何直观表示形式,可借助观测值的散布图表示。
以一元线性回归为例,在散布图上,就是样本残差平方2t e 随解释变量的变化而变化。
ox图(a) y图4.1.1 异方差性在散布图上的反映yxo图(b)图(d) oyyoxx图(c)4.1.2 产生异方差性的原因在计量经济研究中,异方差性的产生原因主要有1.模型中遗漏了某些解释变量 2.模型函数形式的设定误差 3.样本数据的测量误差 4.随机因素的影响4.2 异方差性的影响4.2.1 对模型参数估计值无偏性的影响以一元线性回归模型为例。
设一元线性回归模型为t t t u x b b y ++=10,随机误差项tu 的方差随解释变量的变化而变化:2)var(t t u σ=,其他条件不变。
此时:),0(~2t t N u σ。
在高斯——马尔可夫定理证明过程中曾经得到:t t u k b b ∑+=11ˆ,因此,111)()ˆ(b u E k b b E t t =∑+=。
这表明1b 满足无偏性。
同理可以证明0ˆb 也是0b 的无偏估计量。
由此可见,随机误差项存在异方差性,并不影响模型参数最小二乘估计值的无偏性。
4.2.2 对模型参数估计值有效性的影响在上述假定下参数1b 的估计值1ˆb 的方差为 )var()var()ˆvar(211tt t t u k u k b b ∑=∑+= 在随机误差项t u 同方差的假定下,则参数1b 的估计值1ˆb 的方差为 2222221)()ˆvar(x x k k b t tt -∑=∑=∑=σσσ在随机误差项t u 存在异方差条件下,假设参数估计值为*1ˆb ,2)var(t t u σ==2σλt (0〉t λ,t=1,2,…n ),此时,=)ˆvar(*1b 2222tt ttk k λσσ∑=∑2222t t t tk k k ∑∑⋅∑=λσ=221)ˆvar(tt t k k b ∑∑⋅λ比较上式两端,当122〉∑∑tt t k k λ时,有)ˆvar()ˆvar(1*1b b 〉 从而说明在随机误差项t u 存在异方差条件下,最小二乘估计量1ˆb 不再具有最小方差。


异方差实验报告1. 研究目的本实验旨在探究数据中存在异方差(即方差不等)情况下,不同的方差假设检验方法的效果和正确性。
2. 实验设计为模拟异方差情况,取两个总体样本,其中一个总体样本的方差($\sigma_1^2$)为2,另一个总体样本的方差($\sigma_2^2$)为6,样本容量均为20,采用正态分布。
为了比较不同方差检验方法的效果,此处选择了以下三种方法:(1)方差齐性检验方法:F检验(2)方差近似相等检验方法:T检验(3)无要求的方法:Welch-t检验3. 实验步骤(1)根据上述设计,生成两个总体样本数据,并画图观察其差异。
(2)分别使用上述三种方法进行方差检验,并记录p值和检验结果。
4. 实验结果(1)生成的两个总体样本数据如下图所示:可以看出,两个总体的方差不相等,其中蓝色样本方差明显大于红色样本。
(2)使用三种方法进行方差检验,结果如下:方法|p值|检验结果--|--|--F检验|0.000004|拒绝原假设(方差相等)T检验|0.000021|拒绝原假设(方差相等)Welch-t检验|0.000010|拒绝原假设(方差相等)从结果来看,虽然三种检验方法中最常用的F检验的p值最小,但其在此情况下显然是错误的,因为两个总体的方差明显不相等。
而T检验和Welch-t检验的p值都比较小,而且其结果也正确,即两个总体方差不相等。
5. 结论与分析本实验模拟了数据中存在异方差的情况,通过比较三种方差检验方法的效果,发现在方差不相等情况下,F检验这种方差齐性检验方法是不适用的,而T检验和Welch-t检验这两种方法虽然在某些情况下能够得到相似的结果,但是在此情况下只有Welch-t检验得到了正确的结论。
因此,在实际情况中,如果我们无法保证数据方差相等,应该尽可能使用Welch-t检验,以确保检验结果的正确性。

1、2 实验二 异方差性及其性质 1、2、1 实验目的我们已经知道,在经典条件下,线性模型回归参数的OLS 估计就是具有最小方差的线性无偏估计量。
随机误差项的异方差性,就是线性回归模型中常见的不满足经典条件的情形。
与满足经典条件的情形相比,当模型中出现异方差性时,模型参数的普通最小二乘(OLS)估计的统计性质将发生什么样的变化?如何理解与把握这些变化?如何纠正模型估计因为异方差性而产生的问题?通过本实验,可以帮助学生理解异方差性本身的概念、存在异方差性时模型参数的OLS 估计量的性质、加权最小二乘法等。
1、2、2 实验背景与理论基础 1、 异方差性本实验以二元线性回归模型为例进行说明。
线性回归模型01122i i i i Y X X u βββ=+++,1,2,,i n =L假设模型满足除“同方差性”之外的所有经典假设:(1)E()0i u =,1,2,,i n =L ,或表示为()E =U 0,从而有()E =Y X β; (3)Cov(,)0,i j u u i j =≠,随机误差无序列相关; (4)解释变量就是确定性变量,与随机误差项不相关:Cov(,)0j ij u X =,1,2i =,1,2,,j n =L(5)自变量之间不存在精确(完全)的线性关系。
矩阵X 就是列满秩的:rank()3=X 。
(要求样本容量3n >)(6)随机误差的正态性:2(0,)i u u N σ:,1,2,,i n =L 。
2、 异方差性条件下OLS 估计量的统计性质(1)ˆβ的无偏性: 模型回归参数012,,βββ 的OLS 估计量为:0112ˆˆˆ()ˆβββ-⎛⎫ ⎪''= ⎪ ⎪ ⎪⎝⎭β=X X X Y 可以证明,即使在异方差性条件下,上述估计量依然满足无偏性:0112ˆ()ˆˆE()()ˆ()E E E ββββββ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭β==β (2)ˆβ的方差及协方差: 在模型满足经典条件时,OLS 估计量的方差—协方差矩阵为21ˆVar()()uσ-'=βX X ,但就是在异方差性条件下,不存在独立于X 的随机误差项方差2u σ,因此不再存在这一简单公式。

学院:数学与统计学院专业:数学与应用数学学号::君波实验六方差分析一、实验目的通过本次实验,了解如何进展各种类型均值的比拟与检验。
二、实验性质必修,根底层次三、主要仪器与试材计算机与SPSS软件四、实验容单因素方差分析五、实验学时2学时单因素方差分析(One-Way ANOVA过程)1.某城市从4个排污口取水,进展某种处理后检测大肠杆菌数量,单位面积菌落数如下表所示,请分析各个排污口的大肠杆菌数量是否有差异。
排污口 1 2 3 4 大肠杆菌数量9,12,7,5 20,14,18,12 12,7,6,10 23,13,16,21实验步骤:首先建立“数据视图〞→单击“分析(A)〞→选择“比拟均值〔M〕〞→选择“单因素ANOV A〞→将“大肠杆菌数量〞选入到“因变量列表(E)〞→将“排污口〞选入到“因子〞中→在“选项〔O〕〞中的“描述性〔D〕〞、“方差同质性检验〔H〕〞、“均值图〔M〕〞上打勾→点击“继续〞→点击“确定〞。
运行过程与结果:变量视图:数据视图:运行结果:结果分析:①在“描述〞图表中给出了四个排污口的大肠杆菌数量的根本描述性统计量。
包括样本容量、样本均值、标准差、标准误差、均值的95%的置信区间、最小值和最大值;②在“方差齐性检验〞图表中P值为0.329,假如我们给定显著性水平为0.05,P大于0.05,承受原假设,认为四个总体的方差相等;③在“ANOVA〞图表中假如取显著性水平0.05,因为P=0.003,所以P小于0.05,拒绝原假设,认为各个排污口的大肠杆菌数量存在显著差异;④在“均值图〞中可以看出第四个排污口大肠杆菌数量最多,第一个排污口大肠杆菌数量最少。
2.某连锁商场有五个连锁分店。
希望比拟这五个分店的营业额是否一样,调查人员各自独立地从这五个分店中取得12个营业日的日营业额,资料见下表:连锁店营业日第一分店第二分店第三分店第四分店第五分店1 924 994 1160 1072 9492 1094 1270 1185 1011 11213 1000 1261 1292 961 11594 948 1034 1319 1229 10495 1066 1542 1101 1238 9526 923 1258 1246 1035 10977 823 1215 1340 1240 11448 1035 978 1019 947 9589 1130 1316 1224 1110 91710 1019 1005 967 955 107711 985 944 1221 1091 96712 957 1295 1210 916 1039以α=的显著性水平检验“这五个分店的日营业额一样〞这一假设。
异方差性实验报告doc异方差性实验报告篇一:计量经济学上机实验报告(异方差性)提示:打包保存时自己的文件夹以“学号姓名”为文件夹名,打包时文件夹内容包括:本实验报告、EViews工作文件。
篇二:Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理,以及相关的Eviews操作方法。
【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据,练习检查和克服模型的异方差的操作方法。
【4-16】表4-1给出了美国18个行业1988年研究开发(R&D)费用支出Y与销售收入X的数据。
请用帕克(Park)检验、戈里瑟(Gleiser)检验、G-Q检验与怀特(White)检验来检验Y关于X的回归模型是否存在异方差性?若存在【实验步骤】一检查模型是否存在异方差性1、图形分析检验(1)散点相关图分析做出销售收入X与研究开发费用Y的散点相关图(SCATX Y)。
观察相关图可以看出,随着销售收入的增加,研究开发费用的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
(2)残差图分析首先对数据按照解释变量X由小至大进行排序(SORT X),然后建立一元线性回归方程(LS Y C X)。
因此,模型估计式为: Y?187.507?0.032*X ----------(*) ?(0.17)(2.88) R2=建立残差关于X的散点图,可以发现随着X增加,残差呈现明显的扩大趋势,表明存在递增的异方差。
2、Park检验建立回归模型(LS Y C X),结果如(*)式。
生成新变量序列: GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型(LS LNE2 C LNX)。
从下图所示的回归结果中可以看出,LNX的系数估计值不为0且能通过显著性检验,即随机误差项的方差与解释变量存在较强的相关关系,即认为存在异方差性。
异方差实验报告引言异方差(heteroscedasticity)是指随着自变量的变化,因变量的方差也随之变化的现象。
在统计分析中,假设方差是恒定的是很常见的,但在实际应用中,许多变量的方差是不恒定的,需要进行异方差处理。
本实验旨在通过模拟数据和实际数据来探究异方差的影响并了解异方差检验方法。
实验设计本实验分为两个部分。
第一部分使用模拟数据,提供了不同阶段下的异方差数据集。
第二部分使用实际数据,通过观察数据的模式来判断是否存在异方差。
实验方法模拟数据在模拟数据部分,我们生成了四个数据集,每个数据集都包含一个自变量和一个因变量。
为了模拟异方差,我们设定了不同的标准差,并与自变量呈一定的关系。
具体参数如下:•数据集1:使用正态分布生成自变量和因变量,因变量的标准差为自变量的两倍。
•数据集2:自变量为正态分布,因变量为自变量的2次方,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
•数据集3:自变量为均匀分布,因变量为自变量的指数函数,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
•数据集4:自变量为正态分布,因变量为自变量的对数,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
实际数据在实际数据部分,我们使用了一份销售数据。
该数据包含了不同日期下的产品销售量和价格。
我们首先观察数据的散点图,并通过直观感受来猜测是否存在异方差。
实验结果和分析模拟数据结果分析数据集1数据集1的散点图显示了自变量和因变量之间的线性关系,但由于异方差的存在,随着自变量的增加,因变量的方差也在增大。
这说明了异方差对回归结果的影响。
数据集2数据集2的散点图显示了自变量和因变量之间的非线性关系。
由于自变量的增大,因变量的方差也在增大。
这与模型中设定的异方差关系一致。
数据集3数据集3的散点图显示了自变量和因变量之间的指数关系。
随着自变量的增大,因变量的方差也在增大,符合预期的异方差模式。
数据集4数据集4的散点图显示了自变量和因变量之间的对数关系。