异方差性的检验及处理方法

异方差性在回归分析的影响在回归分析中，异方差性是一个重要的概念，指的是误差项的方差不是恒定的，而是随着自变量的变化而变化。

异方差性会对回归分析的结果产生影响，导致参数估计不准确甚至失真，从而影响对模型的解释和预测能力。

本文将从异方差性的定义、影响、检验以及处理方法等方面展开讨论。

一、异方差性的定义在回归分析中，我们通常假设误差项具有同方差性，即误差项的方差是恒定的。

然而，在实际应用中，误差项的方差可能会随着自变量的变化而发生变化，这种情况被称为异方差性。

异方差性通常表现为误差项的方差与自变量的水平相关，即方差不是常数。

二、异方差性的影响1. 参数估计的不准确性：异方差性会导致参数估计的不准确性，使得回归系数的估计偏离真实值，从而影响对自变量与因变量之间关系的解释。

2. 统计检验的失真：异方差性会使得回归模型的显著性检验结果失真，可能导致错误的结论，影响对模型整体拟合优度的评估。

3. 预测精度的下降：异方差性会影响对未来观测值的预测精度，使得预测结果不可靠，降低模型的预测能力。

三、异方差性的检验为了检验回归模型是否存在异方差性，可以采用以下方法：1. 图形诊断法：通过残差图、残差与预测值的散点图等图形来观察残差的分布情况，如果残差呈现出明显的异方差性模式，就可以怀疑模型存在异方差性。

2. 统计检验法：利用异方差性检验统计量，如White检验、Goldfeld-Quandt检验、Breusch-Pagan检验等，对模型的异方差性进行显著性检验。

四、处理异方差性的方法当检验结果表明模型存在异方差性时，可以采取以下方法进行处理：1. 加权最小二乘法（Weighted Least Squares, WLS）：通过对残差进行加权，使得残差的方差与自变量的水平相关，从而消除异方差性。

2. 变量转换：对自变量或因变量进行对数变换、平方根变换等，使得变量的方差变化较小，减轻异方差性的影响。

3. 引入干扰项：在模型中引入干扰项，如虚拟变量、交互项等，来控制异方差性的影响。

stata异方差检验和解决命令在数据分析中，异方差是一个常见的问题。

异方差指不同样本的方差不相等，这会导致统计结果的不准确性。

Stata提供了许多方法来检验和解决异方差问题。

一、异方差检验检验异方差通常使用Breusch-Pagan-Godfrey(BPG)检验或White检验。

这里以BPG检验为例，该检验的原假设是方差相等，备择假设是方差不相等。

命令格式：estat hettest示例代码：reg y x1 x2 x3estat hettest如果p值小于0.05，则拒绝原假设，说明存在异方差问题。

二、异方差稳健标准误当检测到异方差问题时，可以使用异方差稳健标准误来解决。

异方差稳健标准误在计算系数的标准误时考虑了异方差问题，从而提高了结果的准确性。

命令格式：robust示例代码：reg y x1 x2 x3, robust使用robust命令后，结果中的Standard Error一栏即为异方差稳健标准误。

三、异方差稳健回归如果异方差问题比较严重，只使用异方差稳健标准误可能无法解决问题。

此时可以使用异方差稳健回归。

命令格式：robust示例代码：reg y x1 x2 x3, vce(robust)使用vce(robust)参数后，回归结果中的系数和标准误都是异方差稳健的，并且t值和p值也已经经过了调整。

总结：通过Breusch-Pagan-Godfrey检验或White检验可以检验异方差问题，如果存在异方差问题，可以使用异方差稳健标准误或异方差稳健回归来解决。

在使用robust命令时，不需要进行任何假设检验，因为参数已经考虑了异方差问题。

异方差性的检验及处理方法异方差性是指随着自变量变化，因变量的方差不保持恒定，即方差存在不均匀的变化趋势。

在统计分析中，如果忽视了异方差性，可能会导致误差的不准确估计，从而影响对因变量的显著性检验和参数估计结果的准确性。

为了避免异方差性给统计分析带来的影响，需要进行异方差性的检验和处理。

下面将介绍几种常用的异方差性检验及处理方法。

一、异方差性的检验方法：1.绘制残差图：绘制因变量的残差（观测值与拟合值之差）与自变量的散点图，观察残差是否随着自变量的变化而存在明显的模式。

如果残差图呈现出锥形或漏斗形状，则表明存在异方差性。

2.帕金森检验：帕金森检验是一种常用的检验异方差性的方法。

该方法的原理是通过对残差进行变换，判断变换后的残差是否与自变量相关。

3. 布罗斯-佩根检验（Breusch-Pagan test）：布罗斯-佩根检验是一种常用的检验异方差性的方法。

该方法的原理是通过计算残差与自变量的相关系数，进而判断是否存在异方差性。

4. 品尼曼检验（Leve ne’s test）：品尼曼检验是一种非参数的检验方法，可以用于检验不同组别的方差是否存在显著差异。

二、异方差性的处理方法：1.变量转换：通过对因变量和自变量进行变换，可以使数据满足异方差性的假设。

比如可以对因变量进行对数转换或平方根转换，对自变量进行标准化处理等。

2.使用加权最小二乘法（WLS）：加权最小二乘法是一种可以处理异方差性的回归分析方法。

该方法的原理是通过对残差进行加权，使得残差的方差与自变量无关。

3.使用广义最小二乘法（GLS）：广义最小二乘法是一种可以处理异方差性的回归分析方法。

该方法的原理是通过对残差进行加权，使得残差的方差可以通过自变量的一个线性组合来估计。

4.进行异方差性的鲁棒估计：鲁棒估计是一种对异常值和异方差性具有较好鲁棒性的估计方法。

通过使用鲁棒估计，可以减少异方差性对参数估计的影响。

综上所述，异方差性是统计分析中需要重视的问题。

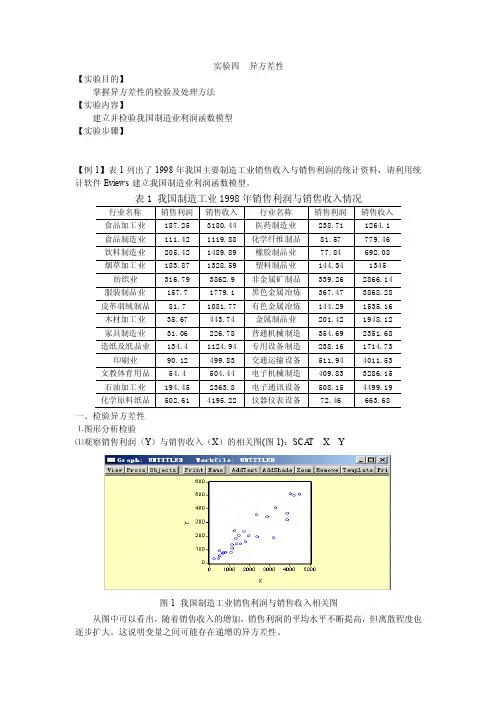
实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料，请利用统计软件Eviews建立我国制造业利润函数模型。

一、检验异方差性⒈图形分析检验⑴观察销售利润（Y）与销售收入（X）的相关图(图1)：SCA T X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出，随着销售收入的增加，销售利润的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

⑵残差分析首先将数据排序（命令格式为：SORT 解释变量），然后建立回归方程。

在方程窗口中点击Resids按钮就可以得到模型的残差分布图（或建立方程后在Eviews工作文件窗口中点击resid对象来观察）。

图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。

⒉Goldfeld-Quant检验⑴将样本按解释变量排序（SORT X）并分成两部分（分别有1到10共11个样本合19到28共10个样本）⑵利用样本1建立回归模型1（回归结果如图3），其残差平方和为2579.587。

SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2（回归结果如图4），其残差平方和为63769.67。

SMPL 19 28LS Y C X图4 样本2回归结果⑷计算F 统计量：12/RSS RSS F =＝63769.67/2579.59=24.72，21RSS RSS 和分别是模型1和模型2的残差平方和。

取05.0=α时，查F 分布表得44.3)1110,1110(05.0=----F ，而44.372.2405.0=>=F F ，所以存在异方差性⒊White 检验⑴建立回归模型：LS Y C X ，回归结果如图5。

图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。

实验报告课程名称：实验项目名称：单方程线性回归模型中异方差的检验与补救院（系）：专业班级：姓名：学号：实验地点：实验日期：年月日实验目的：掌握利用EViews软件对模型中存在的异方差进行检验和补救。

实验内容：根据我国2000年部分地区城镇居民每个家庭平均全年可支配收入X与消费支出Y 的统计数据，通过建立双变量线性回归模型分析人均可支配收入对人均消费支出的线性影响，并讨论异方差的检验与修正过程。

1、异方差的检验1）图示法2）Park检验3）Glejser检验4）Goldfeld-Quandt检验5）White检验2、异方差的补救1）加权最小二乘法（WLS）2）对数变换实验方法、步骤和结果：一、建立工作文件并完成数据输入1、File---new---workfile2、Quick---Empty Group ----paste3、将ser01重命名为x，ser01重命名为y二、写模型的估计方程Quick---Estimate Equation---y c x，得到在不考虑异方差且其他假定都成立的情况下的估计结果，如下图所示：三、异方差的检验找y的估计值在估计结果中点击forcast 将其重命名为yf生成残差序列：在估计窗口中点击proc---make residual series将resid01重命名为res，并保存（一）图示法（对异方差粗略的判定）1.用x-y的散点图进行判断，看是否存在明显的散点扩大、缩小或是复杂性的变动趋势X y ----open----as GroupView---graph ----scatter-----simple scatter2、用y的估计值与残差平方的散点图进行判断，看是否存在一条斜率为零的直线Quick---graph----scatter—写入方程yf res^2图形显示斜率不为零，所以可知模型存在异方差3、任一解释变量x与残差平方的散点图进行判断，看是否存在一条斜率为零的直线Quick—graph—scatter写入方程x res^2图形显示斜率不为零，所以可知模型存在异方差由以上三种图示法可知，模型存在异方差（二）帕克（Park）检验（将图示法公式化）Quick—Estimate Equation---log(res^2) c log(x)由估计结果可知：log（x）=3.703235 P=0.020622<0.05，所以拒绝原假设，模型具有统计显著性，即模型具有异方差。

回归分析中的异方差性检验方法回归分析是统计学中一种常用的数据分析方法，它用来研究自变量和因变量之间的关系。

在进行回归分析时，我们通常会假设误差项的方差是恒定的，即不存在异方差性。

然而，在实际应用中，误差项的方差往往并非恒定的，而是存在异方差性。

异方差性会对回归分析的结果产生影响，因此需要进行异方差性检验并进行相应的修正。

一、异方差性的概念及影响异方差性是指误差项的方差不是恒定的，而是随着自变量的变化而变化。

当存在异方差性时，回归系数的估计值会失真，标准误差会被高估或低估，导致对回归系数和其显著性的检验结果产生偏误。

因此，必须进行异方差性的检验和修正，以确保回归分析结果的准确性和可靠性。

二、异方差性检验方法1. Park检验Park检验是一种常用的异方差性检验方法，它是基于残差的平方和与自变量的关系来进行检验的。

具体步骤是：首先进行回归分析，然后计算残差的平方和，接着将残差的平方和与自变量进行回归，最后通过F检验来检验残差的方差是否与自变量相关。

如果F统计量的显著性水平小于设定的显著性水平（通常为），则拒绝原假设，即存在异方差性。

2. Glejser检验Glejser检验是另一种常用的异方差性检验方法，它是通过对自变量的绝对值进行回归来进行检验的。

具体步骤是：首先进行回归分析，然后计算自变量的绝对值，接着将自变量的绝对值与残差进行回归，最后通过t检验来检验残差的方差是否与自变量相关。

如果t统计量的显著性水平小于设定的显著性水平（通常为），则拒绝原假设，即存在异方差性。

三、异方差性的修正方法1. 加权最小二乘法（Weighted Least Squares, WLS）当检验结果表明存在异方差性时，可以采用加权最小二乘法来进行修正。

加权最小二乘法是通过对残差进行加权，使得残差的方差与自变量的关系消失，从而得到回归系数的一致估计。

2. 广义最小二乘法（Generalized Least Squares, GLS）广义最小二乘法是对加权最小二乘法的推广，它允许误差项之间存在相关性，并对误差项的方差-协方差矩阵进行估计，从而得到回归系数的一致估计。

实验四-异方差性的检验与处理实验四 异方差性的检验及处理（2学时）一、实验目的（1）、掌握异方差检验的基本方法； （2）、掌握异方差的处理方法。

二、实验学时：2学时三、实验要求（1）掌握用MATLAB 软件实现异方差的检验和处理； （2）掌握异方差的检验和处理的基本步骤。

四、实验原理1、异方差检验的常用方法(1) 用X-Y 的散点图进行判断(2). 22ˆ(,)(,)e x e y %%或的图形 ,),x )i i y %%i i （(e 或(e 的图形）(3) 等级相关系数法（又称Spearman 检验）是一种应用较广的方法，既可以用于大样本，也可与小样本。

:i u 0原假设H 是等方差的；:i u 0备择假设H 是异方差；检验的三个步骤① ˆt ty y =-%i e②|i x %%i i 将e 取绝对值，并把|e 和按递增或递减次序排序，计算Spearman 系数rs ,其中：21ni i d =∑s 26r =1-n(n -1)|i x %i i 其中， n 为样本容量d 为|e和的等级的差数。

③ 做等级相关系数的显著性检验。

n>8时，22(2)1s sn t t n r-=--0当H 成立时，/2(2),t t n α≤-若认为异方差性问题不存在；/2(2),t t n α>-反之，若||i i e x %说明与之间存在系统关系，异方差问题存在。

(4) 帕克(Park)检验帕克检验常用的函数形式：若α在统计上是显著的，表明存在异方差性。

2、异方差性的处理方法: 加权最小二乘法 如果在检验过程中已经知道：222()()()i i i ji u Var u E u f x σσ===则将原模型变形为：121()()()()()i i p pi iji ji ji ji ji y x x u f x f x f x f x f x βββ=+⋅++⋅+L 在该模型中：2211()()()()()()i i ji u u ji ji ji Var u Var u f x f x f x f x σσ===即满足同方差性。

异方差性的概念类型后果检验及其修正方法异方差性（heteroscedasticity）是指随着自变量的变化，被解释变量的方差不保持恒定，呈现出不同的分散特征。

异方差性可能会导致线性回归模型的参数估计不精确，误差项的标准误差的估计不准确，常见的检验和修正方法包括Breusch-Pagan检验和White检验，同时，还可以采取加权最小二乘法或者转换变量的方法来修正异方差性。

异方差性可以分为条件异方差和非条件异方差两种类型。

条件异方差是指在给定自变量的情况下，被解释变量方差的大小存在差异；非条件异方差则是指被解释变量的方差在整个样本空间内都存在差异。

异方差性的后果是导致参数估计的不准确性和偏误。

当存在异方差性时，OLS（普通最小二乘法）估计的标准误差会低估真实标准误差，从而使得参数显著性以及模型拟合效果可能出现问题。

此外，在存在异方差性的情况下，t检验、F检验等假设检验的结果也会受到影响。

在进行线性回归模型时，常常需要对异方差性进行检验。

一种常用的检验方法是Breusch-Pagan检验，其基本思想是对残差的平方与自变量进行回归，然后通过F检验来判断异方差的存在与否。

另一种常用的检验方法是White检验，它是在一个包含自变量和交互项的扩展模型中对残差的平方与自变量进行回归，通过Wald检验统计量来判断异方差的存在与否。

异方差性可以通过多种修正方法来处理。

其中，一种常用的方法是采用加权最小二乘法（WLS）来估计参数。

WLS的基本思想是将方差不恒定的观测值加权，使得每个观测值的权重与方差的倒数成正比。

另一种常用的方法是通过转换变量，使得原始数据变换成具有恒定方差的形式，例如对数变换、平方根变换等。

下面以一个案例来说明如何检验和修正异方差性。

假设我们研究了城市的房价（被解释变量）与房屋面积和所在地区（自变量）之间的关系。

我们采集了100个样本数据，并构建了线性回归模型进行分析。

1.检验异方差性：使用Breusch-Pagan检验来检验模型的异方差性。

Z N UE L异方差性的检验方法和修正一、 实验目的熟练掌握异方差性的检验方法和修正处理方法二、实验原理异方差（heteroskedasiticity ）是计量经济工作红线性回归模型经常遇到的问题，异方差的存在对线性回归分析有很强的破坏作用。

利用异方差的图形检验、戈德菲尔特-夸特检验、怀特检验方法，检验案例中线性回归模型的异方差是否存在，若存在的话，如何通过加权最小二乘法进行修正，建立能够真正反应案例的经济模型，实现对经济的正确指导作用。

三、实验要求通过Eviews 软件应用给定的案例做异方差模型的图形检验法、Glodfeld-Quanadt（戈德菲尔特-夸特）检验与White（怀特）检验，并使用加权最小二乘法（WLS）对异方差进行修正。

四、 实验步骤在现实经济活动中，最小二乘法的基本假定并非都能满足，本案例讲讨论随机误差项违背基本假定的一个方面—异方差性。

本案例将介绍：异方差模型的图形检验、戈德菲尔特-夸特检验、怀特检验；异方差模型的加权最小二乘法修正。

1、建立workfile 和对象，录入2007年城镇居民收入X 和消费额Y 的数据。

2、参数估计按住ctrl 键，同时选中序列X 和序列Y ，点右键，在所出现的右键菜单中，选择open\as Group 弹出一对话框，点击其上的“确定”，可生成并打开一个群对象。

在群对象窗口工具栏中点击view\Graph\Scatter\Simple Scatter, 可得X 与Y 的简单散点图，可以看出X 与Y 是带有截距的近似线性关系。

点击朱界面菜单Quick\Estimate Equation, 在弹出的对话框中输入 Y C X,点确定即可到回归结果，如下：VariableCoefficientStd. Errort-StatisticProb. C 756.6871570.1912 1.3270760.1948X0.3076930.01908216.124970.0000R-squared0.899659 Mean dependent var 8689.161Durbin-Watson stat1.694571 Prob(F-statistic)0.0000003、异方差检验本案例用的是2007年的全国各个诚实城镇居民收入和消费额，由于地区之间这种差异使得模型很容易产生异方差，从而影响模型的估计和运行，为此必须对该模型是否存在异方差进行检验。

（完整版）异⽅差性的white检验及处理⽅法实验⼆异⽅差模型的white检验与处理【实验⽬的】掌握异⽅差性的white检验及处理⽅法【实验原理】1. 定性分析异⽅差(1) 经济变量规模差别很⼤时容易出现异⽅差。

如个⼈收⼊与⽀出关系，投⼊与产出关系。

(2) 利⽤散点图做初步判断。

(3) 利⽤残差图做初步判断。

2、异⽅差表现与来源异⽅差通常有三种表现形式（1）递增型（2）递减型（3）条件⾃回归型。

3、White检验（1）不需要对观测值排序，也不依赖于随机误差项服从正态分布，它是通过⼀个辅助回归式构造χ2 统计量进⾏异⽅差检验。

White检验的零假设和备择假设是H0: (4－1)式中的ut不存在异⽅差，H1: (4－2)式中的ut存在异⽅差。

(2)在不存在异⽅差假设条件下，统计量T R 2 ~χ2(5) 其中T表⽰样本容量，R2是辅助回归式(4－3)的OLS估计式的可决系数。

⾃由度5表⽰辅助回归式(4－3)中解释变量项数（注意，不计算常数项）。

T R 2属于LM统计量。

（3）判别规则是若T R 2 ≤χ2α (5), 接受H0（ut 具有同⽅差）若T R 2 > χ2α (5), 拒绝H0（ut 具有异⽅差）【实验软件】Eview6【实验要求】熟练掌握异⽅差white检验⽅法【实验内容】建⽴并检验我国部分城市国民收⼊y和对外直接投资FDI异⽅差模型【实验⽅案设计】下表列出了我国部分城市国民收⼊y和对外直接投资FDI的统计资料，并利⽤统计软件Eviews建⽴异⽅差模型。

地区Y FDI北京32061219126天津26532153473河北1051396405⼭西743521361内蒙古89758854辽宁14258282410吉林933819059⿊龙江1161532180上海46718546849江苏168091056365浙江20147498055安徽645536720福建14979259903江西6678161202⼭东136********河南757053903湖北9011156886湖南7554101835⼴东17213782294⼴西596941856海南831642125重庆720926083四川641841231贵州36034521云南56628384陕西648033190⽢肃50222342青海72772522宁夏66911743新疆97001534【实验过程】1、启动Eviews6软件，建⽴新的workfile.在主菜单中选择【File】--【New】--【Workfile】,弹出Workfile Create对话框,在Workfile structure typ中选择unstructured/undted.然后在observations中输⼊30.在WF中输⼊Work1，点击OK按钮。

检验异方差性与调整异方差性1. 异方差性的概念及检验方法异方差性指的是随机变量的条件方差，并且条件方差不是常数。

也就是说，观测值的方差不仅仅取决于均值，还可能取决于其他因素。

在统计分析中，如果存在异方差性，会对参数估计和假设检验产生影响。

因此，需要在进行统计分析之前，先检验数据是否存在异方差性。

1.1 异方差性检验方法常用的异方差性检验方法有多种，包括：•基于残差的图形检验方法，如残差图和方差-均值图；•基于统计检验的方法，如Levene检验、Bartlett检验以及Brown-Forsythe检验；1.2 基于残差的图形检验方法1.2.1 残差图残差图是一种简单直观的检验异方差性的方法。

在残差图中，横轴表示预测值或观测值的均值，纵轴表示对应的残差。

如果残差的方差与均值无关，则残差图应该呈现出随机分布的特点。

反之，如果残差图中存在明显的模式，即残差的方差与均值相关，则可以初步判断存在异方差性。

1.2.2 方差-均值图方差-均值图是一种更细致的检验异方差性的方法。

在方差-均值图中，横轴表示预测值或观测值的均值，纵轴表示对应的残差的方差。

如果方差-均值图中存在明显的模式，即残差的方差与均值相关，则可以初步判断存在异方差性。

1.3 基于统计检验的方法1.3.1 Levene检验Levene检验是一种常用的检验异方差性的方法。

Levene检验基于修正后的中位数差异进行计算，主要用于检验两个或多个样本之间的方差是否存在显著差异。

在假设检验中，原假设为各组样本方差相等，备择假设为各组样本方差不等。

如果p值小于设定的显著性水平（如0.05），就可以拒绝原假设，认为样本之间存在异方差性。

1.3.2 Bartlett检验Bartlett检验是另一种常用的检验异方差性的方法。

Bartlett检验基于观测值与各组均值差异进行计算，主要用于检验两个或多个样本之间的方差是否存在显著差异。

在假设检验中，原假设为各组样本方差相等，备择假设为各组样本方差不等。

什么是异方差性如何进行异方差性的检验与处理异方差性，它是统计学中一种常见的现象，指的是观测值的方差在不同的条件下不相等。

在数据分析和建模过程中，异方差性可能会导致模型参数估计不准确，假设检验无效以及预测效果下降等问题。

因此，了解异方差性并进行检验和处理是非常重要的。

1. 异方差性的表征异方差性通常表现为残差的方差与预测值的关系不稳定。

在回归分析中，当残差的方差与预测值的关系呈现出一定的模式时，可以初步判断存在异方差性。

常见的异方差性模式有以下几种：（1）线性模式：残差的方差与预测值呈线性关系，即残差的方差随着预测值的增大而增大或减小。

（2）指数模式：残差的方差与预测值呈指数关系，即残差的方差随着预测值的增大呈指数级别增大或减小。

（3）对数模式：残差的方差与预测值呈对数关系，即残差的方差随着预测值的增大呈对数级别增大或减小。

（4）多重峰值模式：残差的方差具有多个峰值，表示不同分组或条件之间存在不同的方差水平。

2. 异方差性的检验针对上述异方差性模式，可以进行一些统计检验来验证异方差性的存在。

常用的异方差性检验方法包括帕金森-斯皮尔曼检验（Park test）、布劳什-帕甘检验（Breusch-Pagan test）和韦斯特曼检验（White test）等。

这些检验方法都是基于残差的方差与预测值之间的关系建立的。

以布劳什-帕甘检验为例，该检验的原假设是残差的方差与预测变量之间不存在显著相关关系，即不存在异方差性。

在进行检验时，首先需要对模型进行拟合，并获得残差。

然后，根据拟合残差和预测变量的关系构建辅助回归模型，并进行显著性检验。

如果辅助回归模型的显著性检验结果小于设定的显著性水平（通常为0.05），则可以拒绝原假设，认为存在异方差性。

3. 异方差性的处理在实际数据分析中，如果检验结果表明存在异方差性，需要对数据进行处理以减小或消除其影响。

常用的异方差性处理方法包括以下几种：（1）对数或平方根变换：通过对原始数据进行对数或平方根变换，可以降低数据的异方差性。

实验二异方差模型的white检验与处理【实验目的】掌握异方差性的white检验及处理方法【实验原理】1. 定性分析异方差(1) 经济变量规模差别很大时容易出现异方差。

如个人收入与支出关系，投入与产出关系。

(2) 利用散点图做初步判断。

(3) 利用残差图做初步判断。

2、异方差表现与来源异方差通常有三种表现形式（1）递增型（2）递减型（3）条件自回归型。

3、White检验（1）不需要对观测值排序，也不依赖于随机误差项服从正态分布，它是通过一个辅助回归式构造χ2 统计量进行异方差检验。

White检验的零假设和备择假设是H0: (4－1)式中的ut不存在异方差，H1: (4－2)式中的ut存在异方差。

(2)在不存在异方差假设条件下，统计量T R 2 ~χ2(5) 其中T表示样本容量，R2是辅助回归式(4－3)的OLS估计式的可决系数。

自由度5表示辅助回归式(4－3)中解释变量项数（注意，不计算常数项）。

T R 2属于LM统计量。

（3）判别规则是若T R 2 ≤χ2α (5), 接受H0（ut 具有同方差）若T R 2 > χ2α (5), 拒绝H0（ut 具有异方差）【实验软件】Eview6【实验要求】熟练掌握异方差white检验方法【实验内容】建立并检验我国部分城市国民收入y和对外直接投资FDI异方差模型【实验方案设计】下表列出了我国部分城市国民收入y和对外直接投资FDI的统计资料，并利用统计软件Eviews建立异方差模型。

地区Y FDI北京32061219126天津26532153473河北1051396405山西743521361内蒙古89758854辽宁14258282410吉林933819059黑龙江1161532180上海46718546849江苏168091056365浙江20147498055安徽645536720福建14979259903江西6678161202山东136********河南757053903湖北9011156886湖南7554101835广东17213782294广西596941856海南831642125重庆720926083四川641841231贵州36034521云南56628384陕西648033190甘肃50222342青海72772522宁夏66911743新疆97001534【实验过程】1、启动Eviews6软件，建立新的workfile.在主菜单中选择【File】--【New】--【Workfile】,弹出Workfile Create对话框,在Workfile structure typ中选择unstructured/undted.然后在observations中输入30.在WF中输入Work1，点击OK按钮。