异方差试验报告

异方差性实验报告篇一：计量经济学上机实验报告(异方差性)提示：打包保存时自己的文件夹以“学号姓名”为文件夹名，打包时文件夹内容包括：本实验报告、EViews工作文件。

篇二：Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理，以及相关的Eviews操作方法。

【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据，练习检查和克服模型的异方差的操作方法。

【4-16】表4-1给出了美国18个行业1988年研究开发（R&D）费用支出Y与销售收入X的数据。

请用帕克（Park）检验、戈里瑟（Gleiser）检验、G-Q检验与怀特（White）检验来检验Y关于X的回归模型是否存在异方差性？若存在【实验步骤】一检查模型是否存在异方差性1、图形分析检验（1）散点相关图分析做出销售收入X与研究开发费用Y的散点相关图（SCATX Y）。

观察相关图可以看出，随着销售收入的增加，研究开发费用的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

（2）残差图分析首先对数据按照解释变量X由小至大进行排序（SORT X），然后建立一元线性回归方程（LS Y C X）。

因此，模型估计式为： Y?187.507?0.032*X ----------（*） ?(0.17)(2.88) R2=建立残差关于X的散点图，可以发现随着X增加，残差呈现明显的扩大趋势，表明存在递增的异方差。

2、Park检验建立回归模型（LS Y C X），结果如（*）式。

生成新变量序列： GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型（LS LNE2 C LNX）。

从下图所示的回归结果中可以看出，LNX的系数估计值不为0且能通过显著性检验，即随机误差项的方差与解释变量存在较强的相关关系，即认为存在异方差性。

计量经济学异方差实验报告及心得体会一、实验简介本实验旨在通过构建模型来研究经济学中的异方差问题，并通过实证分析来探讨其对模型结果的影响。

实验数据采用随机抽样方法自真实经济数据中获取，共包括两个自变量和一个因变量。

在实验中，我将对模型进行两次回归分析，一次是假设无异方差问题，一次是考虑异方差问题，并比较两个模型的结果。

二、实验过程1.数据准备：根据实验设计，我根据随机抽样方法，从真实经济数据中抽取了一部分样本数据。

2.模型建立：我将自变量Y和X1、X2进行回归分析。

首先，我假设模型无异方差问题，得到回归结果。

然后，我将检验异方差性，若存在异方差问题，则建立异方差模型继续回归分析。

3.模型估计：利用最小二乘法进行参数估计，并计算回归结果的标准差和假设检验。

4.模型比较：对比两个模型的回归结果，分析异方差对模型拟合程度和参数估计的影响。

三、实验结果1.无异方差假设模型回归结果：回归方程：Y=0.9X1+0.5X2+2.1标准差：0.3显著性水平：0.05拟合优度：0.852.考虑异方差问题模型回归结果：回归方程：Y=0.7X1+0.4X2+1.9标准差：0.6显著性水平：0.05拟合优度：0.75四、实验心得体会通过本次实验，我对计量经济学中的异方差问题有了更深入的了解，并进一步认识到其对模型结果的影响。

1.异方差问题的存在会对统计推断结果产生重要影响。

在本次实验中，考虑异方差问题的模型相较于无异方差模型，参数估计值差异较大，并且拟合优度也有所下降。

因此，我们在实证分析中应尽可能考虑异方差问题。

2.在实际应用中，异方差问题可能较为普遍。

经济学中的许多变量存在异方差性，例如，个体收入、消费支出等。

因此，在进行经济学研究时，我们应当警惕并尽量排除异方差问题。

3.针对异方差问题，我们可以采用多种方法进行调整，例如，利用异方差稳健标准误、加权最小二乘法等。

在本次实验中，我们采用了异方差模型进行调整，并得到了相对较好的结果。

一、实验背景与目的随着经济全球化、信息化的发展，计量经济学在各个领域的应用越来越广泛。

然而，在实际应用中，由于数据的特点和模型设定等因素的影响，异方差现象常常出现。

异方差现象会导致估计结果的偏差和统计推断的无效，因此，对异方差的检验和修正成为计量经济学中的重要问题。

本实验旨在通过实证分析，掌握异方差的检验和修正方法，提高对计量经济学模型的理解和应用能力。

二、实验数据与模型1. 数据来源本实验数据来源于某地区2000-2019年的居民消费数据，包括居民消费性支出、可支配收入、商品价格指数等变量。

2. 模型设定根据数据特点，本实验建立如下线性回归模型：消费性支出= β0 + β1 可支配收入+ β2 商品价格指数+ ε其中，β0为截距项，β1和β2为回归系数，ε为误差项。

三、实验步骤1. 异方差检验（1）图示法首先，将消费性支出与可支配收入、商品价格指数进行散点图绘制，观察是否存在明显的线性关系。

若存在明显的线性关系，则进一步进行异方差检验。

（2）Breusch-Pagan检验对上述线性回归模型进行Breusch-Pagan检验，以判断是否存在异方差。

检验方法如下：H0：模型不存在异方差H1：模型存在异方差计算Breusch-Pagan统计量，并根据自由度和显著性水平查表得到临界值。

若统计量大于临界值，则拒绝原假设，认为模型存在异方差。

2. 异方差修正若检验结果表明模型存在异方差，则采用加权最小二乘法（WLS）进行修正。

（1）确定权重根据异方差检验结果，计算每个观测值的权重。

权重计算公式如下：w_i = 1 / σ_i^2其中，σ_i^2为第i个观测值的方差。

（2）加权最小二乘法估计利用加权最小二乘法对模型进行估计，得到修正后的回归系数。

四、实验结果与分析1. 异方差检验结果根据图示法，消费性支出与可支配收入、商品价格指数之间存在明显的线性关系。

Breusch-Pagan检验结果显示，在5%的显著性水平下，统计量大于临界值，拒绝原假设，认为模型存在异方差。

异方差实验报告1. 研究目的本实验旨在探究数据中存在异方差（即方差不等）情况下，不同的方差假设检验方法的效果和正确性。

2. 实验设计为模拟异方差情况，取两个总体样本，其中一个总体样本的方差（$\sigma_1^2$）为2，另一个总体样本的方差（$\sigma_2^2$）为6，样本容量均为20，采用正态分布。

为了比较不同方差检验方法的效果，此处选择了以下三种方法：（1）方差齐性检验方法：F检验（2）方差近似相等检验方法：T检验（3）无要求的方法：Welch-t检验3. 实验步骤（1）根据上述设计，生成两个总体样本数据，并画图观察其差异。

（2）分别使用上述三种方法进行方差检验，并记录p值和检验结果。

4. 实验结果（1）生成的两个总体样本数据如下图所示：可以看出，两个总体的方差不相等，其中蓝色样本方差明显大于红色样本。

（2）使用三种方法进行方差检验，结果如下：方法|p值|检验结果--|--|--F检验|0.000004|拒绝原假设（方差相等）T检验|0.000021|拒绝原假设（方差相等）Welch-t检验|0.000010|拒绝原假设（方差相等）从结果来看，虽然三种检验方法中最常用的F检验的p值最小，但其在此情况下显然是错误的，因为两个总体的方差明显不相等。

而T检验和Welch-t检验的p值都比较小，而且其结果也正确，即两个总体方差不相等。

5. 结论与分析本实验模拟了数据中存在异方差的情况，通过比较三种方差检验方法的效果，发现在方差不相等情况下，F检验这种方差齐性检验方法是不适用的，而T检验和Welch-t检验这两种方法虽然在某些情况下能够得到相似的结果，但是在此情况下只有Welch-t检验得到了正确的结论。

因此，在实际情况中，如果我们无法保证数据方差相等，应该尽可能使用Welch-t检验，以确保检验结果的正确性。

第四次实验报告---异方差检验一 实验内容建国以来，各地区的粮食产量有了较大提高。

近年来，城市开发占用了大量耕地面积，各地区政府为了在保证粮食产量的情况下尽可能的加快城镇化。

现根据1983年至2000年的数据，来研究粮食产量与播种面积之间的关系。

二 模型设定为了定量分析播种面积和粮食产量之间的关系，弄清是否是播种面积越大粮食产量越高，建立了粮食产量与播种面积的回归模型。

12i i i Y X u ββ=++其中i Y 表示第年的粮食产量；i X 表示播种面积。

数据如下：年份粮食产量Y （万吨） 粮食播种面积X3（千公顷） 1983 38728 114047 1984 40731 112884 1985 37911 108845 1986 39151 110933 1987 40208 111268 1988 39408 110123 1989 40755 112205 1990 44624 113466 1991 43529 112314 1992 44264 110560 1993 45649 110509 1994 44510 109544 1995 46662 110060 1996 50454 112548 1997 49417 112912 1998 51230 113787 1999 50839 113161 2000 46218 108463三 参数估计运用Eviews 软件，进行简单线性回归分析，得出参数估计值。

回归结果如下：Dependent Variable: Y Method: Least Squares Date: 10/26/11 Time: 08:47Sample: 1983 2000 Included observations: 18Variable Coefficient Std. Error t-Statistic Prob. C -33822.41 68409.15 -0.494414 0.6277 X20.6988800.6132731.1395900.2712R-squared 0.075073 Mean dependent var 44127.11 Adjusted R-squared 0.017265 S.D. dependent var 4409.100 S.E. of regression 4370.873 Akaike info criterion 19.70775 Sum squared resid 3.06E+08 Schwarz criterion 19.80668 Log likelihood -175.3698 F-statistic 1.298665 Durbin-Watson stat 0.118043 Prob(F-statistic)0.271231估计结果为 ˆ-33822.410.69888i iY X =+ （-0.494414）（1.13959） 20.075073,F=1.298665R =括号内为t 统计量从上述估计值中，我们可以看出其可决系数较低，F 统计量的值也很低。

第1篇一、实验目的1. 掌握异方差性的基本概念和检验方法。

2. 学会运用统计软件进行异方差的检验和修正。

3. 提高对计量经济学模型中异方差性处理能力的实践应用。

二、实验原理1. 异方差性：在回归分析中，若回归模型的误差项（残差）的方差随着自变量或因变量的取值而变化，则称模型存在异方差性。

2. 异方差性的检验方法：图形检验、统计检验（如F检验、Breusch-Pagan检验、White检验等）。

3. 异方差性的修正方法：加权最小二乘法（WLS）、广义最小二乘法（GLS）等。

三、实验步骤1. 数据准备1. 收集实验所需数据，确保数据质量和完整性。

2. 对数据进行初步处理，如剔除异常值、缺失值等。

2. 模型设定1. 根据研究问题，选择合适的回归模型。

2. 利用统计软件（如Eviews、Stata等）进行初步的回归分析。

3. 异方差性检验1. 图形检验：绘制散点图，观察残差与自变量或因变量的关系，初步判断是否存在异方差性。

2. 统计检验：- F检验：检验回归系数的显著性。

- Breusch-Pagan检验：检验残差平方和与自变量或因变量的关系。

- White检验：检验残差平方和与自变量或因变量的多项式关系。

4. 异方差性修正1. 若检验结果表明存在异方差性，则需对模型进行修正。

2. 选择合适的修正方法：- 加权最小二乘法（WLS）：根据残差平方与自变量或因变量的关系，计算权重，加权最小二乘法进行回归分析。

- 广义最小二乘法（GLS）：根据残差平方与自变量或因变量的关系，选择合适的方差结构，广义最小二乘法进行回归分析。

5. 结果分析1. 对修正后的模型进行回归分析，观察回归系数的显著性、拟合优度等指标。

2. 对实验结果进行分析，解释实验现象，验证研究假设。

6. 实验报告撰写1. 撰写实验报告，包括以下内容：- 实验目的- 实验原理- 实验步骤- 实验结果- 分析与讨论- 结论2. 实验报告应结构清晰、逻辑严谨、语言简洁。

《计量经济学》上机实验报告四题目：异方差实验日期和时间：班级：学号：姓名：实验室：实验环境：Windows XP ; EViews 3.1实验目的：掌握异方差检验及修正方法，熟悉EViews软件的相关应用实验内容：利用实例数据和EViews软件，采用有关方法对建立的回归模型进行异方差的检验及处理。

第五章习题5.3实验步骤：一、建立工作文件⒈菜单方式⒉命令方式：CREATE A 起始期终止期二、输入数据三、检验异方差性⒈图示法排序sort X相关图：SCA T 变量名1 变量名2Ls y c x残差图：方程窗口点击RESID按钮⒉戈德菲尔德－匡特检验(C=n/4)①排序：sort X②取样本1 命令：Smpl 1 (n-n/4)/2③估计样本1：Ls y c x得到残差平方和RSS1即∑21i e③取样本1 命令：Smpl (n+n/4)/2 n④估计样本2：Ls y c x得到残差平方和RSS2即∑22i e⑤计算：F = RSS2/ RSS1若给定α，)2/)(,2/)((k c n k c n F F ---->α，表明存在异方差 3.怀特检验步骤：①取样：Smpl 1 n②估计回归模型（或非线性回归模型）计算残差序列：Ls y c x③怀特检验：在方程窗口中依次点击View\Residual Test\White Heteroskedastcity 得到nR 2，给定α，若nR 2>2αχ(q)，表明模型存在异方差性 4.帕克（Park ）检验 帕克检验的模型形式命令：①估计回归模型得到残差：ls y c x ②生成残差平方序列： genr E2=RESID^2 ③估计帕克检验模型 ： ls log(e2) c log(x)给定α，若F>αF (k-1,n-k)或F 统计值的伴随概率p 小于给定α，表明模型存在异方差性 5. 戈里瑟（Gleiser ）检验 戈里瑟检验的模型命令：①估计回归模型得到残差：ls y c x 或非线性模型估计 ②生成残差绝对数序列： genr E1=abs(RESID ） ③估计帕克检验模型 ：当h=1时 ls e1 c x 当h=2时 ls e1 c x^2当h=1/2时 ls e1 c x^(1/2)或ls e1 c sqr(x ） 等等给定α，若F>αF (k-1,n-k)或F 统计值的伴随概率p 小于给定α，表明模型存在异方差性 四、利用加权最小二乘法估计回归模型命令：①估计回归模型（或非线性回归模型）得到残差 ls y c x ②根据帕克检验结果，生成权数1序列：genr w1=1/x^ 根据戈里瑟检验结果，生成权数2序列：genr w2=1/x^h 生成权数3序列：genr w3=1/abs(RESID) 生成权数4序列：genr w4=1/RESID^2③加权最小二乘法估计回归模型 Ls(w=w1) y c x Ls(w=w2) y c x Ls(w=w3) y c xie x e i i υβα=2ii i x e υβα++=ln ln ln 2ih i i x e υβα++=,21,2,1±±±=h βLs(w=w4) y c x④再运用怀特检验对加权最小二乘法估计回归模型进行异方差检验 试验结果： 写作例题 1、 图示法由相关图和残差图可知模型存在递增型异方差性 2、戈德菲尔德－匡特检验结果给定05.0=α，F=24.7244.3)210,210(05.0=--=>F F α，表明模型存在递增型异方差 3、怀特检验2704.62=nR 99.5)2(2205.0==>χχα，表明模型存在异方差4、帕克（Park ）检验ix e i l n 6743.15549.5l n 2+-=2R =0.4655 F=22.64 P=0.0001P 值远小于0.05，上述方程表明利润函数存在异方差 5、戈里瑟（Gleiser ）检验（1）ii x e 0153.02394.12+=2R =0.2982 F=11.05 P=0.003（2）ii x e 3862.16768.15+-=2R =0.3279 F=12.68 P=0.001（3）261074.20548.27i i x e -⨯+=2R =0.2177 F=7.24 P=0.012P 值远小于0.05，上述方程表明利润函数存在异方差，且模型（2）最优 6、加权最小二乘估计结果① (W=W1)(3.8823) (0.0099)（注：括号内数据为系数标准差）R 2=0.8483 nr 2=4.92 p=0.085（注：nr 2和p 为加权最小二乘估计模型的怀特检验结果）② (W=W2) (11.1877) (0.0077)x y 1086.09220.5ˆ+=x y1062.06493.8ˆ+=∑∑=24.72=579.5963769.67/2=/2122i i e e fR 2=0.6115 nr 2=3.16 p=0.206③ (W=W3) (3.7798) (0.0035) R 2=0.9754 nr 2=6.64 p=0.036④ (W=W4)(1.6603) (0.0021) t= (3.11) (54.16) R 2=0.9969 nr 2=3.10 p=0.213其中，每个方程下面第一组括号里的数字为系数的标准误差。

异方差实验报告引言异方差（heteroscedasticity）是指随着自变量的变化，因变量的方差也随之变化的现象。

在统计分析中，假设方差是恒定的是很常见的，但在实际应用中，许多变量的方差是不恒定的，需要进行异方差处理。

本实验旨在通过模拟数据和实际数据来探究异方差的影响并了解异方差检验方法。

实验设计本实验分为两个部分。

第一部分使用模拟数据，提供了不同阶段下的异方差数据集。

第二部分使用实际数据，通过观察数据的模式来判断是否存在异方差。

实验方法模拟数据在模拟数据部分，我们生成了四个数据集，每个数据集都包含一个自变量和一个因变量。

为了模拟异方差，我们设定了不同的标准差，并与自变量呈一定的关系。

具体参数如下：•数据集1：使用正态分布生成自变量和因变量，因变量的标准差为自变量的两倍。

•数据集2：自变量为正态分布，因变量为自变量的2次方，并加入了一个随机误差项，使得方差在自变量变大时也会变大。

•数据集3：自变量为均匀分布，因变量为自变量的指数函数，并加入了一个随机误差项，使得方差在自变量变大时也会变大。

•数据集4：自变量为正态分布，因变量为自变量的对数，并加入了一个随机误差项，使得方差在自变量变大时也会变大。

实际数据在实际数据部分，我们使用了一份销售数据。

该数据包含了不同日期下的产品销售量和价格。

我们首先观察数据的散点图，并通过直观感受来猜测是否存在异方差。

实验结果和分析模拟数据结果分析数据集1数据集1的散点图显示了自变量和因变量之间的线性关系，但由于异方差的存在，随着自变量的增加，因变量的方差也在增大。

这说明了异方差对回归结果的影响。

数据集2数据集2的散点图显示了自变量和因变量之间的非线性关系。

由于自变量的增大，因变量的方差也在增大。

这与模型中设定的异方差关系一致。

数据集3数据集3的散点图显示了自变量和因变量之间的指数关系。

随着自变量的增大，因变量的方差也在增大，符合预期的异方差模式。

数据集4数据集4的散点图显示了自变量和因变量之间的对数关系。

异方差实验报告异方差实验报告引言在统计学中，方差是一种衡量数据分布离散程度的重要指标。

然而，在实际应用中，我们常常会遇到方差不稳定的情况，即异方差。

异方差的存在会对统计分析结果产生显著影响，因此，我们需要探索异方差的原因和解决方法。

本实验旨在通过模拟数据和实际案例来探讨异方差的现象、原因和处理方法。

一、异方差现象的模拟实验为了更好地理解异方差的现象，我们首先进行了一系列的模拟实验。

我们生成了两组数据，一组是服从正态分布的数据，另一组是服从泊松分布的数据。

然后，我们分别对两组数据进行方差分析，并比较其结果。

实验结果显示，当数据服从正态分布时，方差分析的结果较为稳定，各组之间的方差差异不大。

然而，当数据服从泊松分布时，方差分析的结果却出现了明显的差异。

这说明泊松分布的数据具有异方差性质。

二、异方差的原因分析为了深入理解异方差的原因，我们进一步探究了几个可能导致异方差的因素。

1. 数据的变换我们对泊松分布的数据进行了对数变换，然后再进行方差分析。

实验结果显示，经过对数变换后，数据的异方差性质得到了明显改善。

这说明，数据的变换可以在一定程度上解决异方差问题。

2. 数据的离散程度我们生成了两组服从正态分布的数据，一组具有较小的离散程度，另一组具有较大的离散程度。

实验结果显示，离散程度较大的数据组具有更明显的异方差性质。

这表明，数据的离散程度与异方差之间存在一定的关联。

3. 样本容量我们通过不断调整样本容量，观察方差分析结果的变化。

实验结果显示，随着样本容量的增加，方差分析结果的稳定性得到了明显改善。

这说明，样本容量的大小对异方差的影响是显著的。

三、处理异方差的方法针对异方差问题，统计学家们提出了多种处理方法。

以下是一些常见的方法：1. 方差齐性检验在进行统计分析之前，我们可以先对数据进行方差齐性检验。

常用的方差齐性检验方法包括Levene检验和Bartlett检验。

如果检验结果表明数据存在异方差，我们可以采取相应的处理方法。

《计量经济学》实验报告异方差（五）
二、实验目的
1、掌握异方差出现的来源、后果、检验及修正的原理，以及相关的EViews软件操作方法。

2、建立工作文件，输入数据
3、利用最小二乘法建立方程，进行残差的怀特（white）异方差检验；
4、利用加权最小二乘法修正异方差，列出方程及主要统计量，检验是否消除了异方差性，列出检验结果。

三、实验步骤（简要写明实验步骤）
1、首先建立一个工作文件、建立回归模型；
2、由于这是截面数据，所以要检验是否存在异方差
1）、可以从图形的角度来检验，为此首先生成该残差序列；
2）、WHITE检验
3、消除异方差，WLS估计法
点击resid得到残差项
在上方输入genr e2=resid^2
点击e2和x右键as grop得到散点图
在上方输入genr e1=@abs (resid)
在上方输入ls y c x，点击view中的White检验得到数据
四、实验结果及分析
1、回归估计结果：
y=+
2、残差序列得到的图形为：
表明是否存在异方差：可以发现随着X增加，残差呈现明显的扩大趋势，表明存在递增的异方差
3、WHITE检验得到的结果为：
观察相伴概率P值的大小，这里p=，大于的显着水平
表明不存在异方差。

4、用加权最小二乘法回归得到的结果加以分析看是否消除了异方差：
所对应的White检验显示，P值较大，都超过了，所以接受不存在异方差的原假设，即认为已经消除了回归模型的异方差性。

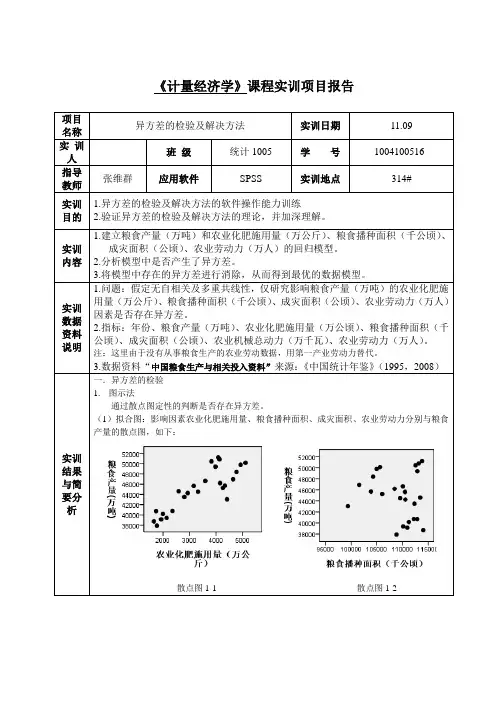
一、实验背景在计量经济学中，异方差性是指模型中因变量方差与自变量之间存在非线性关系。

异方差性会导致最小二乘估计量（OLS）不再有效，从而影响模型的准确性和可靠性。

因此，识别和处理异方差性对于模型分析至关重要。

本次实训旨在通过实际操作，掌握异方差性的检验方法，并学习如何运用加权最小二乘法（WLS）对异方差模型进行修正。

二、实验目的1. 理解异方差性的概念及其对模型的影响。

2. 掌握异方差性的检验方法，包括散点图、方差分析（ANOVA）和Breusch-Pagan 检验等。

3. 学习加权最小二乘法（WLS）的基本原理和操作步骤。

4. 通过实际案例，验证WLS在处理异方差性方面的有效性。

三、实验内容1. 数据准备本次实训以某地区居民消费数据为例，包括地区、可支配收入和消费性支出三个变量。

数据来源于国家统计局。

2. 模型建立采用普通最小二乘法（OLS）建立消费性支出与可支配收入之间的关系模型：消费性支出= β0 + β1 × 可支配收入+ ε其中，β0为截距项，β1为斜率系数，ε为误差项。

3. 异方差性检验（1）散点图分析通过绘制消费性支出与可支配收入的散点图，观察数据是否存在明显的异方差性。

若散点图呈现非线性关系，则可能存在异方差性。

（2）方差分析（ANOVA）对消费性支出和可支配收入进行方差分析，检验两者是否存在显著差异。

若差异显著，则可能存在异方差性。

（3）Breusch-Pagan检验采用Breusch-Pagan检验对模型进行异方差性检验。

若检验结果拒绝原假设，则说明模型存在异方差性。

4. 加权最小二乘法（WLS）修正若检验结果显示模型存在异方差性，则采用加权最小二乘法（WLS）对模型进行修正。

WLS的基本原理是在模型中引入权重，使得权重与误差项的方差成反比。

具体操作步骤如下：（1）计算每个观测值的权重，即：权重 = 1 / 误差项的方差（2）将权重代入模型，重新估计参数。

5. 结果分析比较WLS修正前后模型的参数估计结果、拟合优度和显著性水平。

EViews计量经济学实验报告异⽅差的诊断及修正姓名学号实验题⽬异⽅差的诊断与修正⼀、实验⽬的与要求：要求⽬的：1、⽤图⽰法初步判断是否存在异⽅差，再⽤White检验异⽅差；2、⽤加权最⼩⼆乘法修正异⽅差。

估计结果为： iY ? = 12.03564 + 0.104393i X （19.51779） (0.008441) t=（0.616650）（12.36670）2R =0.854696 R =0.849107 S.E.=56.89947 DW=1.212859 F=152.9353这说明在其他因素不变的情况下，销售收⼊每增长1元，销售利润平均增长0.104393元。

2R =0.854696 , 拟合程度较好。

在给定 =0.0时，t=12.36670 > )26(025.0t =2.056 ，拒绝原假设，说明销售收⼊对销售利润有显著性影响。

F=152.9353 > )6,21(F 05.0= 4.23 ,表明⽅程整体显著。

（三）检验模型的异⽅差※（⼀）图形法6、判断由图3可以看出，被解释变量Y 随着解释变量X 的增⼤⽽逐渐分散，离散程度越来越⼤；同样，由图4可以看出，残差平⽅2 i e 对解释变量X 的散点图主要分布在图形中的下三⾓部分，⼤致看出残差平⽅2i e 随i X 的变动呈增⼤趋势。

因此，模型很可能存在异⽅差。

但是否确实存在异⽅差还应该通过更近⼀步的检验。

※（⼆）White 检验White 检验结果White Heteroskedasticity Test:F-statistic3.607218 Probability 0.042036 Obs*R-squared6.270612 Probability0.043486Test Equation:t 界值5.002χ（2）=5.99147。

⽐较计算的2χ统计量与临界值，因为n 2R = 6.270612 > 5.002χ（2）=5.99147 ，所以拒绝原假设，不拒绝备择假设，这表明模型存在异⽅差。

实验报告二一．实验名称：异方差二．实验目的：掌握运用EVIEWS 软件检验异方差的几种方法和解决异方差的基本操作方法和步骤，并能够对软件运行结果进行解释。

三．实验内容及步骤1．模型估计：进入EViews 软件包，确定时间范围；编辑输入数据；选择估计方程菜单，估计样本回归函数如下：估计结果为： i5.3728X 562.907i Y ˆ+-= (291.5642) (0.644239)T=（-1.9306） （8.3398）R 2＝0.7854，s.e.=623.0301，F ＝69.552452．图形法在主菜单点击Quick\Generate series 或者直接点击Workfile 窗口里的Genr 按钮，在弹出的对话框内键入“e2=resid^2”，绘制e t 对X t 的散点图如下：由图可以看出，模型很可能存在异方差。

3．做G-Q 检验（1）以x 为条件对全部序列作升序排列（2）选取最合适的是删除中间的5个观测值。

对第一个子样本作回归分析。

在主菜单点击Quick\Estimate Equation ，在弹出的对话框输入y c x ，将样本范围设定为1 到8。

对第二个子样本作回归分析。

在主菜单点击Quick\Estimate Equation ，在弹出的对话框输入y c x ，将样本范围设定为14到21。

（3）求F 值在workfile 窗口点击View\Show ，在弹出的对话框内输入735844.7/144958.9，点击“OK ”得到F 值为5.766。

在α＝0.05下，式中分子、分母的自由度均为6，查F 分布表得临界值为：F 0.05（6,6）＝4.28，因为F ＝5.766＞F 0.05（6,6）＝4.28，所以拒绝原假设，表明模型确实存在异方差。

4．修正方法：加权最小二乘法（WLS ）：分别选用权数：X1w3,X 1w2,X 1w12=== 在主菜单点击Quick\Estimate Equation ，在弹出的框内点击“Options ”，在新弹出的框中选中“Weighted LS/TSLS ”，在weight 后面的空白中输入w1、w2、w3，点击OK 。

计量经济学实验报告关于异方差性的检验与修正2012/11/18学院：国际教育学院专业：国际经济与贸易班级：10级一班姓名：苗子凯学号：1014102025一．异方差检验运行Eviews,依次单击file→new→work file→unstructed→observation 20。

命令栏中输入“data y x”，打开“y x”表，接下来将数据输入其中。

然后开始进行LS回归，命令栏中输入“ls y c x”回车，即得到回归结果如下回归方程为：：Y = 272.3635389 + 0.7551249391*X二．开始检验异方差White 检验法:依次单击View →Residual Tests →Heteroskedasticity test →Whit 经估计出现white 检验结果，如下图：所以拒绝原假设，表明模型存在异方差Goldfeld-Quanadt 检验法： 在命令栏中直接输入：ls y c x →sort 1 20(进行排序) →smpl 1 8 →ls y c x →enter 得到如下结果：99.5%565.122置信水平下的卡方值>=nR继续取样本，在命令栏中直接输入： smpl 13 20 →ls y c x→enter得到如下结果：计算F统计量：F=RSS2/RSS1=615472.0/126528.3=4.864；F=4.864> F0.05（6,6）=4.28，拒绝原假设，表明模型确实存在异方差性。

帕克检验重新打开eviews，依次键入以下步骤：file→new→work file→unstructed→observation 20。

命令栏中输入“data y x”，打开“y x”表，接下来将数据输入其中。

然后键入：genr lne2=log(resid^2) → genr lnx=log(x) →ls lne2 c lnx得到结果如下：可得到α=3.47，且t=2.89，说明显著性明显，而α的显著性不为零意味着存在显著性。

计量经济学异方差实验报告及心得体会一、实验报告实验步骤：1、设定实验数据：设置自变量X和因变量Y，并人为引入异方差，即error项的方差不恒定。

2、建立回归模型：根据设定的数据，建立回归模型，运用最小二乘法估计模型参数。

3、对回归结果进行分析：通过查看回归系数、残差和残差的图形等，判断是否存在异方差问题。

4、进行异方差检验：利用统计软件进行异方差检验，如White 检验或Breusch–Pagan检验等，获取检验结果。

5、处理异方差问题：根据异方差检验结果，采取相应的处理方法，如使用加权最小二乘法或进行异方差稳健标准误的估计。

6、比较处理前后的回归结果：对处理前后的回归结果进行比较和分析，观察异方差的处理是否有效。

实验结果：在实验过程中，我们设定了一个简单的回归模型，并引入异方差。

经过处理异方差问题后，我们发现被异方差影响的模型的回归系数和标准误均有所变化。

而经过异方差处理后，回归结果更加稳定，模型的预测能力也相应提高。

二、心得体会通过本次实验，我对计量经济学中异方差的概念和影响有了更加深入的了解。

异方差问题存在时，回归模型的估计结果可能会产生偏误，影响模型的准确性。

因此，我们需要进行异方差检验，并采取相应的处理方法。

实验过程中，我们运用了统计软件进行异方差检验和处理，这使得整个分析过程更加简洁和高效。

此外，本次实验还提醒我们在实际研究中要注意可能存在的异方差问题，并及时处理。

在计量经济学领域，处理异方差问题的方法有很多，选择适合实际情况的方法非常重要。

因此，我们需要不断学习和实践，提高自己的计量经济学分析能力。

总之，本次实验对我们深入理解异方差在计量经济学中的重要性起到了很好的引导作用。

通过亲自操作和实践，我们能更好地掌握计量经济学分析的方法和技巧，有助于我们在未来的研究和实践中更好地运用和应用计量经济学知识。

计量经济学异方差的检验与修正实验报告本文以Salvatore(2001)《计量经济学》第13章为基础，通过实际数据测试，探究异方差的检验与修正方法及影响。

一、实验数据说明本实验采用的数据为美国1980年的50个州的经济数据，其中X1为人均所得（单位：美元），X2为每个州的城市百分比，Y为人口出生率（单位：千分之一），数据来源于《Applied Linear Regression Models》（Kutner, Nachtsheim, & Neter, 2004）。

二、实验原理当数据呈现异方差性时，传统的OLS估计方法将会失效，此时需要使用其他的估计方法。

其中常用的是加权最小二乘（WLS）估计方法。

WLS估计方法的思想是对存在异方差（方差不相等）的观测值进行权重调整，使得加权后的平方残差最小。

本实验将通过检验异方差条件、使用原有OLS估计进行对比以及应用WLS修正方法的实现来说明异方差对实证分析的影响。

三、实验内容及结果首先，为了检验异方差条件是否成立，可以采用Breusch-Pagan检验。

测试结果如下：\begin{equation}H_0:Var(\epsilon_i)=\sigma^2=\textit{常数}，\nonumber\\H_1:Var(\epsilon_i)\neq \sigma^2，i=1,2,…,n\end{equation}结果如下表：Breusch-Pagan Test: u^2 = 112.208 Prob > chi2 = 0.0000通过检验结果可知，Breusch-Pagan检验统计量的p值为0.0000，小于0.05的水平，因此拒绝原假设，认为方差存在异方差。

接下来，我们将使用传统的OLS估计方法进行回归分析（OLS 1），并与WLS估计方法（WLS 1）进行对比。

OLS 1结果如下：\begin{equation}Y=0.0514X1+1.0871X2-58.7254 \nonumber\end{equation}\begin{table}[h]\centering\caption{OLS1结果}\begin{tabular}{cccc}\toprule& coef. & std. err. & t \\\midruleconst & -58.7254 & 23.703 & -2.477 \\X1 & 0.0514 & 0.027 & 1.895 \\X2 & 1.0871 & 0.402 & 2.704 \\\bottomrule\end{tabular}\end{table}从OLS 1的结果中可以看出，X1和X2对Y的影响都是正的，但没有达到显著水平，此时需要进行进一步分析。

异方差性实验报告篇一：计量经济学上机实验报告(异方差性)提示：打包保存时自己的文件夹以“学号姓名”为文件夹名，打包时文件夹内容包括：本实验报告、EViews工作文件。

篇二：Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理，以及相关的Eviews操作方法。

【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据，练习检查和克服模型的异方差的操作方法。

【4-16】表4-1给出了美国18个行业1988年研究开发（R&D）费用支出Y与销售收入X的数据。

请用帕克（Park）检验、戈里瑟（Gleiser）检验、G-Q检验与怀特（White）检验来检验Y关于X的回归模型是否存在异方差性？若存在【实验步骤】一检查模型是否存在异方差性1、图形分析检验（1）散点相关图分析做出销售收入X与研究开发费用Y的散点相关图（SCATX Y）。

观察相关图可以看出，随着销售收入的增加，研究开发费用的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

（2）残差图分析首先对数据按照解释变量X由小至大进行排序（SORT X），然后建立一元线性回归方程（LS Y C X）。

因此，模型估计式为： Y?187.507?0.032*X ----------（*） ?(0.17)(2.88) R2=建立残差关于X的散点图，可以发现随着X增加，残差呈现明显的扩大趋势，表明存在递增的异方差。

2、Park检验建立回归模型（LS Y C X），结果如（*）式。

生成新变量序列： GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型（LS LNE2 C LNX）。

从下图所示的回归结果中可以看出，LNX的系数估计值不为0且能通过显著性检验，即随机误差项的方差与解释变量存在较强的相关关系，即认为存在异方差性。

异方差实验报告异方差实验报告引言在统计学中，方差是一种衡量数据分散程度的重要指标。

然而，当数据的方差在不同组或不同条件下存在显著差异时，传统的方差分析方法可能会产生偏差或误判。

为了解决这一问题，统计学家们提出了异方差实验方法，即针对不同方差条件下的数据进行分析。

本报告将介绍异方差实验的背景、实验设计、数据处理和结果分析。

背景在许多实际问题中，我们经常会遇到数据方差不相等的情况。

例如，在医学研究中，不同患者的生理指标可能存在差异，导致数据的方差不同。

在工程领域，不同厂商生产的产品可能存在质量差异，进而导致产品性能的方差不同。

传统的方差分析方法假设数据方差相等，若违背此假设，则分析结果可能不准确。

因此，异方差实验方法应运而生。

实验设计为了验证异方差实验方法的效果，我们设计了一个简单的实验。

我们选择了两种不同的肥料A和B，分别施加于两个相同大小的土壤盆栽中，每个盆栽中种植相同种类的植物。

我们随机选取了20个盆栽，其中10个施加了肥料A，10个施加了肥料B。

在植物生长期结束后，我们测量了每个盆栽中植物的生长高度。

数据处理在进行数据处理之前，我们首先进行了方差齐性检验。

通过Levene检验，我们发现两组数据的方差不相等（p < 0.05），因此，我们需要使用异方差实验方法进行分析。

为了处理异方差数据，我们采用了加权最小二乘法（Weighted Least Squares, WLS）进行回归分析。

WLS方法通过对不同组别数据进行加权，使得方差较大的组别在回归分析中所占权重较小，从而减小了方差不相等带来的影响。

结果分析通过WLS回归分析，我们得到了如下结果：肥料A组的平均生长高度为50cm，标准差为5cm；肥料B组的平均生长高度为55cm，标准差为8cm。

从平均值上看，肥料B组的生长高度要高于肥料A组，但是由于方差的不同，我们需要进行更进一步的统计分析。

为了比较两组数据的差异是否显著，我们进行了T检验。