平面直角坐标系的建立共24页文档

建立平面直角坐标系的步骤第一部分：引入直角坐标系的概念1.介绍直角坐标系的定义：直角坐标系又称笛卡尔坐标系，是由垂直相交的两条数轴（一条横轴和一条纵轴）组成的。

2.解释直角坐标系的用途：直角坐标系可以用于描述平面上的点的位置和表示矢量的方向和大小。

3.引入直角坐标系的标记法：在直角坐标系中，每个点都可以用一个有序对(x,y)表示，其中x表示横轴上的位置，y表示纵轴上的位置。

第二部分：确定坐标轴的位置和方向4.确定横轴（x轴）的位置：通常情况下，横轴被放置在平面的底部，向右延伸。

可以采用尺子或直尺量取平面上的适当长度，并确定横轴的位置。

5.确定纵轴（y轴）的位置：纵轴垂直于横轴，并通过横轴上的一些点，向上延伸。

可以使用量角器或直角板来确定纵轴与横轴的垂直关系。

6.确定坐标轴正方向：在确定坐标轴的方向时，需要选择一个轴作为正方向。

通常情况下，横轴的正方向是从左到右，纵轴的正方向是从下到上。

第三部分：确定单位长度和比例尺7.确定单位长度：需要选择一个适当的单位长度来表示平面上的距离。

常用的单位包括米、厘米、毫米等。

选择一个合适的单位长度，使得平面上的点的坐标更容易计算。

8.确定比例尺：比例尺是将实际长度映射到坐标上的尺度比例。

可以根据实际应用需求选择合适的比例尺。

比例尺的选择应该使得平面上的点的坐标更容易理解和计算。

第四部分：绘制坐标轴和坐标点9.绘制坐标轴：使用尺子或直尺在平面上画出确定好的横轴和纵轴。

需要保证坐标轴的长度适当，可以根据实际需求确定。

10.绘制坐标点：根据给定的点的坐标，在坐标轴上定位这些点。

可以使用尺子或直尺，在横轴和纵轴上找到相应的位置，并用图形和标记表示。

第五部分：使用直角坐标系描述和计算11.使用直角坐标系表示点的位置：根据给定点的坐标，将这些点在直角坐标系中标注出来。

可以使用线段、圆圈或点来表示。

12.使用直角坐标系计算点的位置：可以使用直角坐标系计算点之间的距离、斜率和角度等。

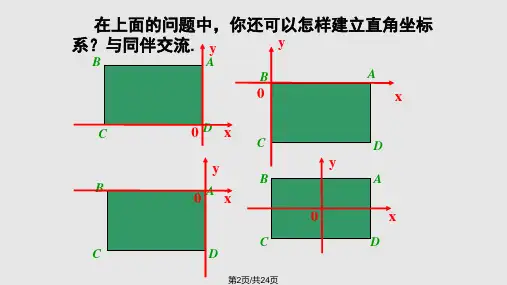
平面直角坐标系建立方法嘿，咱今儿就来讲讲平面直角坐标系建立方法，这可是个很有意思的事儿呢！你看啊，平面直角坐标系就像是一个大棋盘，每个点都有它独特的位置。

那怎么建立这个神奇的“棋盘”呢？首先，咱得找个平整的地方，就像盖房子得有块好地基一样。

然后，在这个地方画出一条直直的线，这就是横轴啦，也叫 x 轴。

嘿，你说这 x 轴像不像一条大公路，上面跑着各种数字呢！接下来，再画一条和它垂直的线，这就是纵轴，也就是y 轴咯。

哇，这两条线一交叉，立马就有感觉了，是不是？就像十字路口一样，一下子就热闹起来了。

那这两条轴上得有刻度呀，就跟尺子上的刻度似的。

咱给它们标上数字，从左到右，从下到上，这样每个点就能找到自己对应的位置啦。

你想想，要是没有这些刻度，那可就乱套啦，就跟在一个没地图的地方瞎转悠一样。

建立好了平面直角坐标系，那就可以在上面玩啦！可以标记各种点，比如说一个苹果在这儿，一个橘子在那儿。

哈哈，多有意思呀！而且哦，通过这个坐标系，咱还能做很多厉害的事情呢。

比如说算距离呀，看图形呀。

就好像给这些点都穿上了小衣服，一下子就能认出来啦。

你说这平面直角坐标系是不是很神奇？它就像是我们探索数学世界的一张大地图，有了它，我们就能在数学的海洋里畅游啦！咱平时生活中不也经常用到类似的东西嘛，比如说地图呀，那也是一种坐标嘛。

你想找个地方，就得看着地图上的坐标去找，是不是跟平面直角坐标系一个道理呀。

所以啊，可别小瞧了这个平面直角坐标系的建立方法，它可是打开数学大门的一把钥匙呢！学会了它，咱就能在数学的世界里尽情玩耍啦，还等什么呢，赶紧去试试吧！。

平面直角坐标系的建立在几何学中，平面直角坐标系是一种常用的工具，用于描述平面上的点的位置。

它由两条互相垂直的数轴组成，分别称为x轴和y轴。

本文将介绍平面直角坐标系的建立步骤以及其在几何学中的应用。

一、平面直角坐标系的建立步骤要建立平面直角坐标系，需要以下几个步骤：1.选择原点：原点是平面上的一个点，被用作坐标的起点。

在建立平面直角坐标系时，通常选择一个便于计算的点作为原点。

2.确定x轴和y轴的方向：x轴和y轴分别代表水平方向和垂直方向。

在建立平面直角坐标系时，需要确定它们相互垂直且方向相反。

3.确定单位长度：在平面直角坐标系中，需要确定一个单位长度，用于表示每个单位的长度。

通常情况下，单位长度可以是任意长度，但为了方便计算，常选择1个单位长度等于1个长度单位（如1个单位长度等于1米）。

4.绘制坐标轴：在平面上绘制出x轴和y轴，并且确保它们相互垂直。

可以使用尺子和直尺等工具来帮助绘制。

5.标注坐标轴：在绘制的坐标轴上标注刻度值，以表示具体的位置。

刻度值可以根据需要进行标注，通常从原点开始逐渐增加或减小。

二、平面直角坐标系的应用平面直角坐标系在几何学中有广泛的应用，可以用来描述点、直线、曲线等几何图形的位置和性质。

1.表示点的位置：在平面直角坐标系中，每个点可以用一个有序数对表示，称为坐标。

其中第一个数表示点在x轴上的位置，第二个数表示点在y轴上的位置。

例如，点A的坐标为（2，3），表示该点在x轴上距离原点2个单位长度，在y轴上距离原点3个单位长度。

2.表示直线的方程：在平面直角坐标系中，可以使用方程来表示直线的位置和性质。

例如，直线的一般方程为Ax + By + C = 0，其中A、B、C为常数。

通过这样的方程，可以描述直线在坐标系中的位置和斜率等特征。

3.计算距离和斜率：平面直角坐标系可以帮助计算点与点之间的距离和直线的斜率。

对于两个点A(x1, y1)和B(x2, y2)，它们之间的距离可以计算为d = √((x2 - x1)^2 + (y2 - y1)^2)。

平面直角坐标系的构建方法介绍在数学和几何学中，平面直角坐标系是一种常用的坐标系，用于描述平面上的点的位置。

这份文档将介绍平面直角坐标系的构建方法。

构建步骤1. 选择原点：首先，在平面上选择一个点作为坐标系的原点。

原点可以位于任何位置，通常选择一个便于计算的位置，如图中的交叉点或者平面的中心。

选择好原点后，用大写字母"O"来表示原点。

2. 确定坐标轴：在原点处，画两条互相垂直的线，分别表示x 轴和y轴。

x轴通常水平显示，而y轴则垂直与x轴。

在x轴上选择一个正方向，并在y轴上选择另一个正方向。

通常，我们选择x 轴向右为正方向，y轴向上为正方向。

用小写字母"x"和"y"表示坐标轴。

3. 刻度和单位：在坐标轴上刻度表示距离。

刻度可以用等距离的小线段或数字来表示。

选择适当的刻度间距，以便于测量和绘图。

确定好刻度后，标上合适的单位，如米、厘米等。

4. 标记点的坐标：为了表示平面上不同点的位置，我们需要为每个点标记坐标。

在平面直角坐标系中，点的坐标表示为一个有序对(x, y)，其中x表示点在x轴上的距离，y表示点在y轴上的距离。

5. 绘制点：根据标记的点坐标，可以在相应的位置绘制点。

使用一个小圆点或其他合适的符号来表示点。

6. 连接点：如果需要，可以使用直线或曲线来连接多个点，以形成线段、线或曲线。

示例下图展示了一个平面直角坐标系的示例：- 原点: O- 坐标轴: x轴和y轴- 刻度和单位: 每个小刻度代表1个单位- 标记的点: A(2, 3)、B(-1, 4)、C(5, -2)、D(-3, -1)- 连接点: AC、BD等线段和线结论通过选择原点、确定坐标轴、刻度和单位、标记点的坐标，以及绘制和连接点，我们可以构建一个平面直角坐标系，用于在平面上表示点的位置。

平面直角坐标系在数学、几何学和其他领域中有广泛的应用。

平面直角坐标系示意图
介绍
平面直角坐标系是数学中常用的坐标系，用于描述二维平面上的点。

本文档将详细介绍平面直角坐标系的构成和使用方法。

坐标系的构成
平面直角坐标系由两条互相垂直的直线组成，通常被称为x轴和y轴。

这两条轴交于原点(0,0)，形成四个象限，分别记作第一象限、第二象限、第三象限和第四象限。

坐标的表示
平面直角坐标系中的每个点都可以用一个有序数对(x。

y)来表示。

其中，x表示点在x轴上的位置，y表示点在y轴上的位置。

x 轴上的正方向可以取为右侧，y轴上的正方向可以取为上方。

坐标的特点
第一象限中的点，x坐标和y坐标都是正数。

第二象限中的点，x坐标是负数，y坐标是正数。

第三象限中的点，x坐标和y坐标都是负数。

第四象限中的点，x坐标是正数，y坐标是负数。

坐标的使用方法
平面直角坐标系常用于图形的描述和计算。

通过确定点在坐标系中的位置，可以计算点之间的距离、直线的斜率等。

示例
以下是一个使用平面直角坐标系表示的点和直线的示例：
点A的坐标为(2.5)
点B的坐标为(-3.1)
直线AB的斜率为(1/5)
结论
平面直角坐标系是一种常用的数学工具，用于描述二维平面上的点和图形。

通过了解坐标系的构成和使用方法，我们可以方便地进行二维几何计算和分析。

以上就是关于平面直角坐标系的简要介绍，希望对您有帮助。

参考文献：
Smith。

J。

(2018)。

___ Magazine。

90(1)。

9-15.。