最新人教版四年级图形的运动知识点归纳以及练习题

四年级数学下册第七单元《图形的运动二》知识点
把一个图形沿着某一条直线对折，如果直线两旁的部分能够完全重合，我们就说这个图形是轴对称图形，这条直线叫做这个图形的对称轴。

注：1、对称轴是一条直线，所以在画对称轴时，要画到图形外面，且要用虚线。

2、轴对称图形可以有或对称轴。

3、画轴对称图形时，先找到与相反方向距离对称轴相同的对称点，最后连线。

1、
都是轴对称图形。

2、长方形有2条对称轴，正方形有4条对称轴，等腰梯形有1条对称轴，菱形有2条对称轴
3、等腰三角形有1条对称轴，等边三角形有3条对称轴，
4、线段有1条对称轴，圆有无数条对称轴，半圆有1条，圆环有无数条，半圆环有1条。

5、平行四边形不是轴对称图形，没有对称轴。

（长方形和正方形除外）
6、梯形不一定是轴对称图形。

只有等腰梯形是轴对称图形。

知识拓展：古今中外，许多著名的建筑就是对称的。

比如：中国的赵州桥，印度泰姬陵，英国塔桥，法国埃菲尔铁塔等。

平移：平移与移动的方向和距离有关，平移不改变图形的形状和大小，但改变了图形的位置。

1、先确定物体平移的方向，再通过某一点或某一条边确定平移的距离，找准对应点，对应线段。

2、利用平移求不规则图形的面积时，一般把不规则图形通过平移得到规则图形，再求面积。

第12讲图形的运动（二）知识点一：平移1.确定平移的方法和距离：（1）根据箭头指向确定平移的方向；（2）找出平移前后两个图形的一组对应点，对应点之间的格数就是图形平移的格数。

2.画简单图形平移后的图形的方法：（1）找出已知图形的关键点；（2）将关键点按要求平移相应的格数，得到一组对应;（3）根据原图形的形状将对应点按顺序连接。

考点1：平移的特征【典例1】2．（成武县期末）通过平移、、可以得到的是（）A．B．C．【典例2】．（裕华区期中）下面（）的运动是平移。

A．转动呼啦圈B．拧螺丝钉C．火箭升空【典例3】（上街区期末）如图中的阴影部分是一块菜地，这块菜地的面积是平方米．【典例4】（成都期中）在平移的过程中，得到的图形与原来图形的和都相同．考点2：画平移后的图形【典例1】根据△和O现在的位置和规定的走法，在格子图里画出△和O行走的路线．（1）△先向右走5格，再向上走2格．（2）O先向左走6格，再向下走2格．【典例2】（玛纳斯县校级期中）汽车向平移了格；飞机向平移了格；蘑菇向平移了格．综合练习一．选择题1．（北川县期末）下面图案（）是经过平移得到的．A．B．C．D．2．（承德期末）下列现象中，不属于平移的是（）A．乘坐电梯B．钟表上的指针运动C．火车行驶3．（陕州区期末）由如图的小鱼图平移后得到的图形是（）A．B．C．4．（龙口市期中）下面现象（）是平移。

A．用卷笔刀削铅笔B．用扳手拧螺丝C．电梯的升降D．风车的转动5．（洪泽区校级期中）把一个图形在方格纸上先向下平移2格，再向右平移6格，再向下平移2格的位置（）A．相同B．不相同C．不一定相同6．（龙州县期末）如图中的图形向右平移了（）格．A．7B．5C．3二．填空题7．（深圳期末）（如图）平行四边形ABCD由两块七巧板拼组而成．②号三角板不动，将①号三角板向平移格，可与②号三角板重新拼成一个正方形．8．（五莲县期末）如图，由图A到图B是向平移了格，由图B到图C是向平移了格．9．（随州期末）三角形先向平移了格，再向平移了格．小船先向平移了格，再向平移了格．三．判断题10．汽车在笔直的公路上行驶，车身做平移运动．（判断对错）11．（微山县期末）一个图形不论是向左平移还是向下平移，它的形状和大小都不变．（判断对错）12．（法库县校级期中）一个图形经过平移后，它的大小和形状发生了改变。

四年级图形运动练习题在四年级学习数学的过程中，图形运动是重要的一部分。

通过图形运动的练习，可以帮助学生理解和掌握几何图形的特性，提高他们的观察能力和空间想象能力。

本文将为四年级学生提供一些图形运动的练习题，帮助他们巩固所学知识。

1. 小球运动在一张纸上画一个圆，表示小球的位置。

按照以下指令，描述小球的运动轨迹。

指令：- 向前滚动三个单位- 向右滚动两个单位- 向左滚动四个单位- 向上滚动五个单位2. 正方形变换在一张纸上画一个正方形，边长为3个单位。

按照以下指令，描述正方形经过变换后的位置和形状。

指令：- 沿着顺时针方向旋转90度- 边长减少一个单位- 沿着逆时针方向旋转45度- 边长增加两个单位3. 矩形移动在一张纸上画一个矩形，长边为4个单位，短边为2个单位。

按照以下指令，描述矩形的移动轨迹。

指令：- 向右平移三个单位- 向上平移一个单位- 向左平移两个单位- 向下平移四个单位4. 圆形变换在一张纸上画一个圆，半径为2个单位。

按照以下指令，描述圆经过变换后的位置和形状。

指令：- 半径增加一个单位- 向左平移两个单位- 半径减少一个单位- 向右平移三个单位通过以上的练习题，四年级的学生可以对图形运动有更深入的理解。

在解题的过程中，他们需要运用到平移、旋转和缩放等几何变换的概念，同时也提高了他们的逻辑思维和空间想象能力。

通过反复练习，他们可以熟练掌握这些知识。

除了练习题，老师还可以设计一些趣味性的游戏来帮助学生学习图形运动。

例如，学生可以自己设计图形运动的指令，让同学们按照指令进行绘画，看谁画出来的图形最接近预期结果。

这样的游戏既能培养学生的创造力，又能够加深对图形运动的理解。

总之，图形运动是四年级数学学习中重要的一部分。

通过练习题和趣味游戏的形式，学生可以深入理解和掌握图形运动的概念和方法。

希望本文提供的练习题对学生有所帮助，让他们在数学学习中取得更好的成绩。

图形运动初步知识点总结一、图形的运动图形的运动是指图形在平面内沿特定路径进行变换的过程。

图形的运动有平移、旋转和翻转三种基本形式，同时还包括旋转、放大缩小和组合等多种衍生形式。

1. 平移平移是指图形在平面内沿着某一方向进行移动，保持图形的大小和形状不变。

平移的特点是图形的各个部分同时保持相同的方向和距离进行移动，因此平移是不改变图形的位置关系和大小形状的变换。

2. 旋转旋转是指图形绕某一点或某一条直线进行转动的变换。

旋转的特点是图形的各个部分绕着旋转中心进行旋转，在旋转过程中保持图形的大小和形状不变。

3. 翻转翻转是指图形沿着某一直线进行对称变换的过程。

翻转的特点是图形的各个部分绕着对称轴进行翻转，翻转后的图形和原图形是关于对称轴对称的。

4. 旋转、放大缩小和组合除了平移、旋转和翻转外，图形的运动还包括旋转、放大缩小和组合等多种衍生形式。

旋转是指图形绕着某一点或某一直线进行旋转的变换，放大缩小是指图形按照比例进行整体伸缩的变换，而组合是指两种或两种以上的基本运动形式结合进行的复合运动。

二、图形的描述对图形的运动进行描述时，一般需要确定图形的基本特征和运动的方式。

图形的基本特征包括位置、大小和形状三个方面，而运动的方式则包括平移、旋转和翻转等多种形式。

1. 位置位置是指图形在平面内的具体位置。

对于平面直角坐标系中的图形，位置可以通过坐标值来描述；而对于平面极坐标系中的图形，位置则可以通过极坐标来描述。

2. 大小大小是指图形在平面内的具体大小。

对于平面直角坐标系中的图形，大小可以通过图形的长、宽或者直径等尺寸来描述；而对于平面极坐标系中的图形，大小则可以通过极径来描述。

3. 形状形状是指图形在平面内的具体形状。

对于平面直角坐标系中的图形，形状可以通过图形的轮廓或边缘线条来描述；而对于平面极坐标系中的图形，形状则可以通过图形的曲线类型来描述。

三、图形的表示对图形的运动进行表示时，一般可以通过坐标变换和矢量变换两种方式来进行。

第11讲图形的运动知识点一：轴对称1、对称轴的定义：把一个图形沿着某一条直线对折，如果直线两边的图形能完全重合，那么这个图形就叫轴对称图形。

这条直线叫对称轴。

特征：对折后左右两边完全重合的图形是轴对称图形。

注意：物体的对称性与轴对称图形这两个概念是不同的。

“对称性”是某些物体的特征，“轴对称”是部分平面图形的特征。

2、轴对称图形概念的几种表述：（1）如果一个图形沿着一条直线对折，折痕两侧的图形能够完全重合，这个图形就是轴对称图形。

（2）一个图形可以用一条直线平分成两半，并且这两半完全相同，这个图形就是轴对称图形。

（3）对折后能完全重合的图形就是轴对称图形。

以上三种概念表述说明：轴对称图形是一个两部分能完全重合的图形。

3、类型：左右对称或上下对称的图形，都是轴对称图形。

常见的轴对称图形有：长方形、正方形、圆形、等边三角形。

字母是轴对称图形的有：A、B、C、D、E、H、I、 K、M、O、T、V、U、W、X、Y。

4、画图：根据轴对称图形的一半，画出它的另一半。

A.画对称轴的方法：左右对称的图形，在它左右两边的最上端找到一组相对称的点，并量出这两个点的中点。

然后在最下端量出一组对称点的中点。

最后经过这两个中点划出一条虚线。

（上下对称的图形画法相似）B.根据对称轴画出轴对称图形的另一半的方法：先将已知图形的每个角的顶点，在对称轴的另一端，以对称轴为中点量出与它们的相对称的点。

最后将这些点用已知图形的连接方法一一连接起来。

（记住：找对称点时，必须以对称轴为中心。

）考点1：轴对称图形的辨识【典例1】（峨山县）把一张正方形纸按如下方法对折两次后，在如图所示的位置上打一个孔，把纸展开后得到的应是（）A．B．C．D．【典例2】（常州期末）如图的图形中，有（）个沿着虚线对折两边能完全重合．A．1B．2C．3考点2：镜面对称问题【典例1】（西安期末）小明早晨起床锻炼时，从镜子看到的时间如下图所示，回家时从钟表上看到的时间也如下图所示．小明起床的时间是时分；他锻炼了小时．【典例2】（海安县模拟）星期日，菲菲到蓝猫家去玩，玩着玩着，想知道现在的时间，刚抬起头，从镜子中看见了挂钟显示的是6:30，聪明的菲菲眼珠一转，就知道了真实的时间．同学们，你们知道吗？考点3：做轴对称图形及画对称轴【典例1】（岳阳模拟）在如图每一个虚线框中补画一个小正方形，使补画后的图形成为轴对称图形，并画出每个图形的对称轴．【典例2】（瑞昌市校级模拟）画出下列各图形的对称轴，有几条就画几条．综合练习一．选择题（共8小题）1．（莲湖区期中）如图的图形沿虚线对折后，会变成哪个图形？（）A．B．C．D．2．（临漳县期中）如图将一张正方形纸对折后，按上面虚线剪开，展开后是（）字。

图形的运动（一）对称轴的知识点1、对称轴的定义：把一个图形沿着某一条直线对折，如果直线两边的图形能完全重合，那么这个图形就叫轴对称图形。

这条直线叫对称轴。

特征：对折后左右两边完全重合的图形是轴对称图形。

注意：物体的对称性与轴对称图形这两个概念是不同的。

“对称性”是某些物体的特征，“轴对称”是部分平面图形的特征。

2、轴对称图形概念的几种表述：（1）如果一个图形沿着一条直线对折，折痕两侧的图形能够完全重合，这个图形就是轴对称图形。

（2）一个图形可以用一条直线平分成两半，并且这两半完全相同，这个图形就是轴对称图形。

（3）对折后能完全重合的图形就是轴对称图形。

以上三种概念表述说明：轴对称图形是一个两部分能完全重合的图形。

3、类型：左右对称或上下对称的图形，都是轴对称图形。

常见的轴对称图形有：长方形、正方形、圆形、等边三角形。

字母是轴对称图形的有：A、B、C、D、E、H、I、K、M、O、T、V、U、W、X、Y。

4、画图：根据轴对称图形的一半，画出它的另一半。

A.画对称轴的方法：左右对称的图形，在它左右两边的最上端找到一组相对称的点，并量出这两个点的中点。

然后在最下端量出一组对称点的中点。

最后经过这两个中点划出一条虚线。

（上下对称的图形画法相似）B.根据对称轴画出轴对称图形的另一半的方法：先将已知图形的每个角的顶点，在对称轴的另一端，以对称轴为中点量出与它们的相对称的点。

最后将这些点用已知图形的连接方法一一连接起来。

（记住：找对称点时，必须以对称轴为中心。

）(二)平移的知识点1.确定平移的方法和距离：（1）根据箭头指向确定平移的方向；（2）找出平移前后两个图形的一组对应点，对应点之间的格数就是图形平移的格数。

2.画简单图形平移后的图形的方法：（1）找出已知图形的关键点；（2）将关键点按要求平移相应的格数，得到一组对应;（3）根据原图形的形状将对应点按顺序连接。

3.应用平移进行图形的变换。

（教材第87页例4）这道题该如何解决：运用图形的平移可以将不规则图形转化成规则图形，进而解决问题。

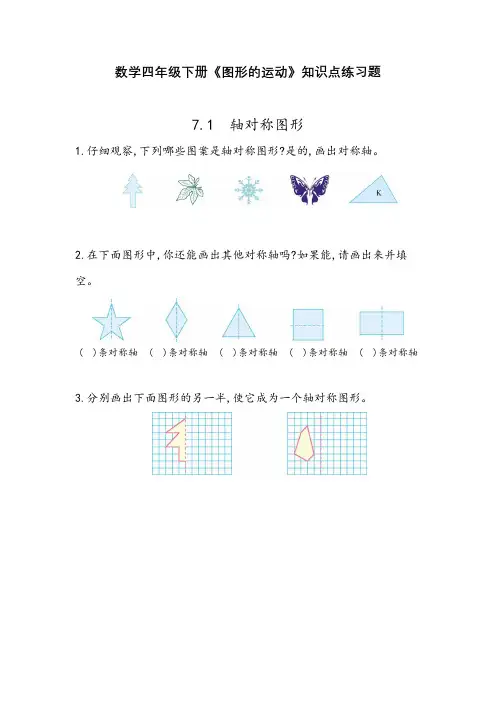
数学四年级下册《图形的运动》知识点练习题7.1 轴对称图形1.仔细观察,下列哪些图案是轴对称图形?是的,画出对称轴。

2.在下面图形中,你还能画出其他对称轴吗?如果能,请画出来并填空。

()条对称轴()条对称轴()条对称轴()条对称轴()条对称轴3.分别画出下面图形的另一半,使它成为一个轴对称图形。

附答案：1.2. 5、2、3、4、23.7.1轴对称图形一、填空。

1、如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是（），折痕所在的直线叫做（）。

2、圆的对称轴有（）条，半圆形的对称轴有（）条。

3、（）三角形有三条对称轴，（）三角形有一条对称轴。

4、正方形有（）条对称轴，长方形有（）条对称轴，等腰梯形有（）条对称轴。

二、选择题。

1、下列英文字母中，是轴对称图形的是（）A、SB、HC、PD、Q2、下列图形中：角、线段、直角三角形、等边三角形、长方形，其中一定是轴对称图形的有（）A、2个B、3个C、4个D、5个3、下列图形中，对称轴最多的是（）。

A、等边三角形 B 、正方形 C 、圆 D、长方形4、下面不是轴对称图形的是（）。

A、长方形B、平行四边形C、圆D、半圆三、操作题：1、试找出如图所示的每个正多边形的对称轴的条数，并填下表格中．答案:一、1、对称图形对称轴2、无数一条3、等边等腰4、 4, 2, 1二、B B C B三、2、 3 4 5 6 7 87.21.填一填。

(1)点A到对称轴的距离是()格,点A'到对称轴的距离是()格。

(2)点B到对称轴的距离是()格,点B'到对称轴的距离是()格。

2.画出轴对称图形的另一半。

3.在下图中补画一个同样大小的正方形,使整个图形成为轴对称图形。

附答案：1.2格 2格 3格 3格2.3.7.2图形的平移一、将图中的小船向左平移5格。

二、画一画：梯形先向下平移2格，再向左平移7格。

三、你能把小亭子图从左上方平移到右下方吗？想一想，有几种方法能实现。

四年级下数学《图形的运动》知识点总结归纳
一、基本概念
1.图形运动：图形在平面内按照某种规律或路径进行移动，但不发生翻转或变形。

2.平移：图形在平面内沿某一方向直线移动一定的距离，不发生旋转。

3.旋转：图形围绕某一点转动一定的角度，不发生移动。

二、平移性质
1.平移不改变图形的形状、大小和方向。

2.平移后，对应点所连的线段与平移方向平行且等长。

3.平移后，对应线段平行且等长，对应角相等。

三、旋转性质
1.旋转不改变图形的形状、大小和方向。

2.旋转后，对应点到旋转中心的距离相等，对应线段相等，对应角相等。

3.旋转后，图形上对应点到旋转中心的距离等于旋转半径，对应线段与旋转半径
相等，旋转中心到图形上任意一点的距离都是相等的。

四、平移与旋转的区别与联系
1.区别：平移是沿某一方向直线移动一定的距离；旋转是围绕某一点转动一定的
角度。

2.联系：平移可以看作是旋转（围绕某一点）在直线上的表现形式；旋转也可以
看作是平移（沿某一方向）在圆周上的表现形式。

五、图形运动的实例
1.平移实例：火车在铁轨上行驶、电梯上下移动、推拉门等。

2.旋转实例：风力发电机叶片的转动、车轮的转动、旋转木马等。

通过本节课的学习，学生将了解图形运动的基本概念和平移、旋转的性质，掌握图形运动的基本规律，并能够在实际生活中应用这些知识解决一些实际问题。

第7讲图形的运动（二）轴对称概念特点把一个图形沿着某一条直线对折，如果直线两侧的部分能完全重合，那么这个图形就是轴对称图形这条直线就是这个图形的对称轴，互相重合的点叫做对应点，也叫做对称点性质对称点到对称轴的距离相等把描出的对称点按顺序连线，得到轴对称图形的另一半确定所给图形的关键点，也就是图形上每条线段的端点确定关键点的对称点平移特点画法图形的大小和形状都不变，只改变图形的位置先找出原图形的关键点，然后按照平移的方向和距离找出关键点的对应点，最后连线应用求不规则图形的面积知识梳理知识点一：轴对称1. 把一个图形沿着某一条直线对折，如果直线两侧的部分能完全重合，那么这个图形就是轴对称图形。

这条直线就是这个图形的对称轴，互相重合的点叫做对应点，也叫做对称点。

2. 轴对称图形的性质：对称点到对称轴的距离相等。

3.补全轴对称图形的方法：（1）确定所给图形的关键点，也就是图形上每条线段的端点；（2）确定关键点的对称点 ;（3）把描出的对称点按顺序连线，得到轴对称图形的另一半。

知识点二：平移1.图形在平移前后只是位置发生了变化，大小形状是不变的。

2.画出平移后的图形，必须要确定其方向和距离。

确定平移的距离可以数对应点移动的距离，也可以数对应线移动的距离。

3.平移的实际运用平移不规则图形规则图形转化面积不变考点一：轴对称例1．（2018秋•石家庄期末）由第一行的剪纸能得到第二行的哪个图形，把它们连在一起．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此判断即可．【解答】解：【点评】掌握轴对称图形的意义，判断是不是轴对称图形的关键是找出对称轴，看图形沿对称轴对折后两部分能否完全重合．1．（2014春•西安期中）画出下边图形在镜子中的图形．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：画出下边图形在镜子中的图形：【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．2．（2014春•海淀区校级期末）右面是镜子中看到的时间，请画出现实的时间．【分析】根据镜面对称的性质求解，在平面镜中的像与现实中的事物恰好左右顺序颠倒，且关于镜面对称．【解答】解：根据镜对称，画现实时间如下：故答案为：【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反．3．（2014春•简阳市校级期末）画出已知图形关于直线a的轴对称图形．【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的右边画出左图的关键对称点，连结即可．【解答】解：根据分析，作轴对称图形如下：【点评】本题是考查作轴对称图形，关键是把对称点画正确．考点二：平移例2．（2015秋•甘州区校级期中）看图填空．（1）图2小飞机先向上平移4格，再向左平移6格得到图1．（2）图3小房子先向右平移7格，再向下平移4格得到图4．【分析】根据平移的特征：找出两个图形平移的对应关键点，即可得到平移的方向和距离，由此得解．【解答】解：（1）图2小飞机先向上平移4格，再向左平移6格得到图1．（2）图3小房子先向右平移7格，再向下平移4格得到图4．故答案为：4，左，6；7，下，4．【点评】本题是考查图形的平移，方向关键看箭头指向，距离关键看对应点相距几格．1．（2015春•揭阳期末）图①向左平移了7格．图②向右平移了7格．图③向下平移了6格．图④向上平移了6格．【分析】根据题意，结合图形，由平移的概念找出图形平移的方向和平移的格数，即可求解．【解答】解：图①向左平移了7格．图②向右平移了7格．图③向下平移了6格．图④向上平移了6格．故答案为：左，7，右，7，下，6，上，6．【点评】本题考查平移的基本概念及平移规律，是比较简单的几何图形变换．关键是要观察比较平移前后物体的位置．2．（2014秋•洪泽县校级期末）（1）图中长方形向下平移了5格；（2）图中六边形向左平移了6格；（3）图中五角星向右平移了4格．【分析】（1）上边的长方形和下边的长方形的各对应点相差5格，箭头方向指向下，因此，下边的长方形是由下边长方形向下平移5格得到的；（2）左边的六边形和右边的六边形的各对应点相差6格，箭头方向指向左，因此，左边六边形是由右边六边形向左平移6格得到的；（3）右边的五角星和左边的五角星的各对应点相差4格，箭头方向指向有，因此，右边五角星是由左边五角星向右平移4格得到的．【解答】解：（1）图中长方形向下平移了5格；（2）图中六边形向左平移了6格；（3）图中五角星向右平移了4格；故答案为：下，5，左，6，右，4．【点评】本题主要是考查平移的意义．3．（2014秋•普宁市校级期中）说一说，填一填．（1）☆向右平移3格（2）〇向下平移4格（3）□向上平移3格（4）△向左平移3格．【分析】平移是指在平面内，将一个图形上的所有点都按照某个方向作相同距离的移动叫做平移运动，简称平移；由此结合题意进行解答即可．【解答】解：（1）☆向右平移3格（2）〇向下平移4格（3）□向上平移3格（4）△向左平移3格．故答案为：右，3，下，4，上，3，左，3．【点评】此题考查了简单图形平移，找到关键点，进行关键点的平移，向什么方向平移，平移多少是解决此题的关键．巩固提升1．（2020春•成武县期末）将长度为6厘米的线段向左平移10厘米，平移后的线段长（）A．6厘米B．16厘米C．10厘米【分析】平移：在平面内，将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。

人教版小学四年级数学下册同步复习与测试讲义第七章图形的运动（二）【知识点归纳总结】1.轴对称1．轴对称的性质：像窗花一样，把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，称这两个图形为轴对称，这条直线叫做对称轴，两个图形中的对应点叫做对称点．把一个图形沿着某一条直线折叠，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴．2．性质：（1）成轴对称的两个图形全等；（2）如果两个图形成轴对称，那么对称轴是对称点连线的垂直平分线．【经典例题】例：如果把一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形．分析：依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，据此即可进行解答．解：据分析可知：如果把一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形．故答案为：一条直线、完全重合、轴对称图形．点评：此题主要考查轴对称图形的意义．2.镜面对称1．镜面对称：有时我们把轴对称也称为镜面（镜子、镜像）对称，如果沿着图形的对称轴上放一面镜子，那么在镜子里所放映出来的一半正好把图补成完整的（和原来的图形一样）．2．将镜面看做对称轴，那么关于镜面对称的像关于对称轴对称．【经典例题】例：如图是小明在镜子中看到的钟表的图象，他表示的真实时间是（）A、4：40B、4：20C、7：20D、7：40分析：根据镜面对称的性质，在平面镜中的像与现实中的事物恰好左右颠倒，且关于镜面对称，分析并作答．解：根据镜面对称的性质，分析可得题中所显示的时刻与4：40成轴对称，所以此时实际时刻为4：40；故选：A．点评：本题考查镜面反射的原理与性质．解决此类题应认真观察，注意技巧．3.平移1．平移：把一个图形整体沿某一方向移动一定的距离，图形的这种移动，叫做平移．2．平移后图形的位置改变，形状、大小不变．【经典例题】例：电梯上升是（）现象．A、旋转B、平移C、翻折D、对称分析：平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动．电梯的升降是上下位置的平行移动所以是平移，据此解答判断．解：电梯的升降是上下位置的平行移动，所以电梯的升降是平移现象；故选：B．点评：本题主要考查平移的意义，在实际当中的运用．【同步测试】单元同步测试题一．选择题（共10小题）1．下图中，BC的长度是6厘米，点B到对称轴的距离是（）厘米．A．3厘米B．4厘米C．6厘米D．12厘米2．补全轴对称图形的时候，要先找到（）A．边界B．对称轴C．端点3．从镜子中看到现在是4时，正确的时间是（）A．4时B．8时C．2时4．如图从镜子中看到的图形是（）A．B．C．5．下列哪种现象属于平移（）A．荡秋千B．乘坐电梯C．翻书6．小红在镜子里看到墙上的挂钟如图所示，请问第（）个时间最接近8：00．A．B．C．D．7．是从（）上剪下来的．A．B．C．D．8．如图是小明在平面镜中看到时钟形成的像，它的实际时间是（）A．21：05B．12：02C．12：05D．15：029．下列图（）是由如图平移得到的．A．B．C．D10．笑笑非常喜爱《小英雄雨来》中“我们是中国人，我们爱自己的祖国”这句话，于是她自己刻了一枚如左图所示的印章．下面四个图案中用这枚印章印制的是（）A．B．C．D．二．填空题（共8小题）11．如图的钟面是从镜子里看到的，实际钟面上的时刻是．12．如图，由图A到图B是向平移了格，由图B到图C是向平移了格．13．拨动算盘是现象．14．一个图形对折后，两边能够完全，这个图形是，这条折痕所在的直线叫做．15．在一幅轴对称图形中，沿对称轴对折后A点与B点重合．如果A点到对称轴的距离是4厘米，那么未对折前A点到B点的距离是厘米．16．在平面镜里看到背后墙上，电子钟示数如图所示，这时的时间应是．17．小明在镜子中看到钟面上是4：30，实际钟面上是．18．被列为非物质文化遗产的陕北剪纸，通过现场操作等多种形式，让市民体验到了传统技艺的妙趣．某市民将一个正方形彩纸依次按如图1、图2所示的方式对折，然后沿图3中的虚线裁剪，则将图3的彩纸展开铺平后的图形是图4中的．（填序号）三．判断题（共5小题）19．两个圆组成的图形一定是轴对称图形．（判断对错）20．是轴对称图形．（判断对错）21．平移改变了图形的位置，形状和大小．（判断对错）22．从镜子中看到左图的样子是这样的．．（判断对错）23．淘气举左手时，镜子中的淘气举右手．．（判断对错）四．操作题（共2小题）24．如图，图形①经过怎样的运动可以得到图形②？25．下面的图案各是从哪张纸上剪下来的？请连线．五．解答题（共3小题）26．看图填空①（1）向平移了格．②（2）向平移了格．③（3）向平移了格．27．请你用三种不同的方法分别图中添画一个小正方形，使它成为一个轴对称图形．28．从镜子中看到的左边图形的样子是什么？请在认为正确的图形上画“√”．参考答案与试题解析一．选择题（共10小题）1．【分析】依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，对称点到对称轴的距离相等，所以BC的长度是6厘米，点B到对称轴的距离是6÷2＝3（厘米）；据此即可进行解答．【解答】解：因为对称点到对称轴的距离相等，所以，BC的长度是6厘米，点B到对称轴的距离是6÷2＝3（厘米）．故选：A．【点评】此题主要考查轴对称图形的意义以及对称轴的性质运用．2．【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在补全轴对称图形的时候，首先在对称轴的另一边画出原图的关键对称点，然后依次连结即可完成轴对称图形．据此解答．【解答】解：由分析得：在补全轴对称图形的时候，首先在对称轴的另一边画出原图的关键对称点，然后依次连结即可完成轴对称图形．故选：C．【点评】此题考查的目的是理解掌握轴对称图形的特征及应用．3．【分析】根据镜面对称的性质求解，在平面镜中的像与现实中的事物恰好左右顺序颠倒，且关于镜面对称．【解答】解：从镜子中看到现在是4时，正确的时间是8时；故选：B．【点评】本题是考查镜面对称，白镜面对称的特点是：上下前后方向一致，左右方向相反．4．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：如图故选：B．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．5．【分析】把一个图形整体沿某一方向移动一定的距离，图形的这种移动，叫做平移．根据平移不改变图形的形状、大小和方向，结合图形对选项进行一一分析，选出正确答案．【解答】解：荡秋千、翻书，运动过程中改变了方向，不符合平移的性质；乘坐电梯，符合平移的性质，故属于平移；故选：B．【点评】本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．6．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称，我们画出这几个钟面所表示的时刻，即可得知第几个时间最接近8：00．【解答】解：如图，图A与8：00相差5分，图B与8：00相差30分，图C和图D与8：00相差3小时45分，最接近8：00的时图A．故选：A．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．7．【分析】作出这个图形的纵向对称轴，看左侧与下面哪个图形的空缺部分相吻合，就是从哪个图形上剪下来的．【解答】解：如图故选：C．【点评】把一张纸对折后，在对折边处剪出的图形是以纸的折痕为对称轴的轴对称图形．8．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：如图实际时间是12：05．故选：C．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．9．【分析】图形平移后，只是位置的变化，图形大小、形状、方向不变．A图、B图、D图大小没变，但方向变了，不是原图平移后得到的；C图大小、形状、方向没变，是原图平移后的图形．【解答】解：经过平移后得到即图形C是由原图平移得到的．故选：C．【点评】关键抓住平移的特征：图形平移后，只是位置的变化，图形大小、形状、方向不变．10．【分析】印章与印出的图案如同镜面对称，根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称，也就是印章与印出的图案上、下一致，左右方向相反，大小不变．【解答】解：如图，故选：B．【点评】关键明白印章与印出的图案如同镜面对称，根据镜面对称原理进行选择．二．填空题（共8小题）11．【分析】镜面对称的特点是：上下前后方向一致，左右方向相反；图中镜子里看到的时间是6：40，由镜面对称左右方向相反特点，镜中时针在6与7之间，实际是在5与6之间，是5时，镜中分针指刻度8，实际中是指刻度4，即20分；据此解答．【解答】解：因为镜中时针在6与7之间，实际是在5与6之间，是5时，镜中分针指着刻度8，实际中是指刻度4，即20分，所以实际钟面上的时刻是5：20．故答案为：5：20．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反．12．【分析】根据图中两图的相对距离及箭头指向即可确定平移的方向和距离，所以图A到图B是向右平移了6格，由图B到图C是向下平移了2格；由此解答即可．【解答】解：如图，由图A到图B是向右平移了6格，由图B到图C是向下平移了2格．故答案为：右，6，下，2．【点评】作图形平移要注意三要素：即原位置、平移方向、平移距离．13．【分析】平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动．拨动算盘是上下位置的平行移动，据此解答．【解答】解：拨动算盘是上下位置的平行移动，所以拨动算盘是平移现象．故答案为：平移．【点评】本题主要考查平移的意义，在实际当中的运用．14．【分析】依据轴对称图形的定义即可作答．一个图形沿着某一条直线折叠，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴．【解答】解：一个图形对折后，两边能够完全重合，这个图形是轴对称图形，这条折痕所在的直线叫做对称轴．答案为；重合，轴对称图形，对称轴．【点评】此题主要考查轴对称图形的定义．15．【分析】依据轴对称图形的特点，即轴对称图形是指一个图形沿一条直线折叠后直线两旁的部分能够完全重合，这条直线就是这个轴对称图形的对称轴．轴对称图形中，对称点到对称轴的距离相等．【解答】解：4×2＝8（厘米）答：如果A点到对称轴的距离是4厘米，那么未对折前A点到B点的距离是8厘米．故答案为：8．【点评】此题主要考查轴对称图形的特点．16．【分析】根据镜面对称的性质，在平面镜中的像与现实中的事物恰好左右颠倒，且关于镜面对称，分析并作答．【解答】解：根据镜面对称的性质，分析可得题中所显示的时刻与21：05成轴对称，所以此时实际时刻为21：05．故答案为：21：05．【点评】本题考查镜面反射的原理与性质．解决此类题应认真观察，注意技巧．17．【分析】根据镜面对称的性质求解，在平面镜中的像与现实中的事物恰好左右相反，且关于镜面对称．【解答】解：根据镜面对称的性质，题中所显示的时刻成轴对称，所以此时实际时刻为7：30．故答案为：7：30．【点评】本题考查镜面反射的原理与性质．解决此类题应认真观察，注意技巧．18．【分析】找一张纸，按照图中的顺序向上对折，再向左对折，按位置剪去画的虚线的形状，然后展开即可．【解答】解：经过动手操作，发现将图3的彩纸展开铺平后的图形是图4中的第四个图．故答案为：④．【点评】此题主要考查轴对称图形的意义和动手操作的能力．三．判断题（共5小题）19．【分析】两个圆无论半径相等，还是不相等，无论是相交、相切或相离、还是内含，组成的图形都是轴对称图形，只对称轴的条数多少而已，最多是两个圆组成环形，有无数条对称轴，最少有一条对称轴．【解答】解：两个圆组成的图形一定是轴对称图形原题说法正确．故答案为：√．【点评】无论两个圆的大小如何，位置关系怎样，所组成的图形一定是轴对称图形．20．【分析】根据对称轴的定义：如果一个图形沿着一条直线对折，两侧的图形能完全重合，这个图形就是轴对称图形．折痕所在的这条直线叫做对称轴，据此即可进行判断．【解答】解：根据轴对称图形的意义可知：是轴对称图形，说法正确；故答案为：√．【点评】解答此题的主要依据是：轴对称图形的意义及特征．21．【分析】平移是指在平面内，将一个图形上的所有点都按照某个方向作相同距离的移动．平移不改变图形的形状和大小，只是改变位置；把一个图形绕着某一点转动一个角度的图形变换叫做旋转，旋转时图形位置发生变化，大小不变，形状不变．【解答】解：平移只改变了图形的位置，没有改变图形的形状，故原题说法错误；故答案为：×．【点评】本题是考查平移的特点、旋转的特点．旋转与平移的相同点：位置发生变化，大小不变，形状不变，都在一个平面内．不同点：平移，运动方向不变．旋转，围绕一个点或轴，做圆周运动．22．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．【解答】解：从镜子中看到左图的样子是这样的．故答案为：×．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．23．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：如图淘气举左手时，镜子中的淘气举右手．原题的说法是正确的．【点评】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．四．操作题（共2小题）24．【分析】据平移的意义“平移是指在同一平面内，将一个图形整体按照某个直线方向移动一定的距离，这样的图形运动叫作图形的平移运动，简称平移”，由此可知：把图①向下平移4格再向右平移5格即可得到图②；由此解答即可．【解答】解：根据平移的性质可知：把图①向下平移4格再向右平移5格即可得到图②．【点评】本题是考查平移图形的特征，平移和旋转不改变图形的形状和大小，平移不改变图形的方向，旋转则改变图形的方向．25．【分析】图案左起第一个和第二个不同，每个花瓣上有凹陷第二个没有，第二个有柄，第一个没有，第三个是心型，第四个是葫芦型，第一个连第二行的左起第三个，每二个连每四个，第三个连第一个，第四个连第二个．【解答】解：根据分析连线如下：【点评】本题是考查图形的组拼，相似的要注意观察细微部位．五．解答题（共3小题）26．【分析】把一个图形整体沿某一方向移动一定的距离，图形的这种移动，叫做平移，据此解答即可．【解答】解：①（1）向上平移了2格．②（2）向左平移了4格．③（3）向右平移了6格．故答案为：上，2，左，4，右，6．【点评】本题是考查作平移后的图形，注意，一看方向（左、右、上、下），二看对应点（或边）距离几格．27．【分析】依据轴对称图形的含义，即在平面内，如果一个图形沿一条直线对折，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，据此即可完成作图．【解答】解：如图所示，即为所要求的画图：【点评】解答此题的主要依据是：轴对称图形的意义及特征．28．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：根据镜面对称，如下图：【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．。

人教版四年级图形的运动知识点归纳以及练习题1.轴对称（1）轴对称图形的定义如果一个平面图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴（2）轴对称图形的基本性质对应点到对称轴的距离相等，对称的两部分的大小相等，形状相同，只是方向相反。

（3）补全一个轴对称图形的方法①确定已知图形的关键点，如图形的顶点，交点，端点等②数出或量出关键点到对称轴的距离③在对称轴的另一侧描出关键点的对应点④按照已知那一般图形的形状顺次连接各赌赢点，把轴对称图形补充完整练习：1.画对称轴画出下列图形的对称轴画对称轴时要注意，该图形有几条对称轴就画出来几条2.补全轴对称图形3.长方形有（）条对称轴，正方形有（）条对称轴，圆有（）条对称轴4.把一张长方形纸片折叠，使BC边落在FE处，折痕为GH，梯形AGHD和梯形GHEF的面积分别是25cm²和20cm²，原长方形的面积是多少？2.平移（1）平移的含义一个简单的物体按照一定的方向（向上或向下或向左或向右）和距离从一个位置移动到另一个位置，这个构成叫做平移平移后的图形与平移前的图形大小相等，形状相同，只是所在位置发生了变化（2）画出平移后的图形的方法①要确定平移的图形的关键的点②确定平移的方向和长度③描出关键定平移后的对应点，按照已知图形的形状顺次连接各对应点，即可画出平移后的图形（3）通过切割---平移---填补的方法解决实际问题练习：1.分别画出将图形向上平移四个格，再向右平移12个格，最后向下平移7个格的图形2.求下列图形的面积：3.画出下列轴对称图形的另一半，并画出这个轴对称图形向左平移16个格，在向下平移6个格后得到的图形4.求下图的面积：5.你能算出，一只蚂蚁从这个楼梯爬一次所经过的路程有多少米吗？6.下面是一个椭圆形公园的平面图，中间有一个圆形的游泳池，求这个公园的陆地面积7.如图，某小区有一块长为42m、宽22m的长方形草坪，先要在草坪里铺设一横两纵三条等宽的甬道，已知每条甬道的宽度都是2m，求铺设甬道后草坪的面积。