人教版四年级图形的运动知识点归纳以及练习题

第七单元图形的运动（二）-四年级数学下册易错点汇总及优选易错题A卷本单元知识点易错汇总：1. 对称轴是一条直线。

射线、线段都不能称为图形的对称轴。

2. 轴对称图形中连接对称点的线段一定垂直于对称轴并被对称轴平分。

3. 轴对称图形被对称轴分成的两部分沿对称轴对折后能够完全重合。

4. 图形平移的距离是指对应点之间的距离，而不是指两个图形之间空格的距离。

5. 在对图形进行两次平移时，一定要正确理解题意，明确平移的顺序、方向和距离。

6. 把不规则图形转化为规则图形的方法往往不止一种。

（时间：60分钟，总分：100分）一．选择题（满分16分，每小题2分）1．图中，能通过平移得到的是()A．B．C．2．下面的图形，哪个从中间对折，不能完全重合。

()A．B．C．3．下列现象，()不是平移现象。

A．B．C．4．下列是平移的是()A．升旗时国旗上下运动B．风车转C．电风扇转动5．补全轴对称图形的时候，要先找到()A．边界B．对称轴C．端点6．画出轴对称图形的另一半相当于将其()A．翻转B．平移C．对折7．是从()纸上剪下来的．A．B．C．D．8．下面现象属于平移的是()A．B．C．二．填空题（满分16分，每小题2分）9．小兔子先向走格就能吃到白菜，再向走格就能吃到萝卜了。

10．一幅轴对称图形沿对称轴对折后A点与B点重合，如果A点到对称轴的距离是4厘米，那么B点到对称轴的距离是厘米。

11．将一个图形向上平移3格，它的没有变化，发生了变化．12．早晨7点10分，妈妈叫醒小明，让他起床，可小明从镜子中看到的时刻还没有到起床的时刻，他对妈妈说：“还早呢！”小明误以为当时是点分．13．一个图形对折后，两边能够完全，这个图形是，这条折痕所在的直线叫做．14．拨动算盘是现象．15．图中的三角形向平移了格．16．一个图形不论往上（下)，左（右)方向平移，它们的和没有变，只有变了。

三．判断题（满分8分，每小题2分）17．观察一个图形的平移过程，只需观察该图形上任意一点的平移过程．18．汽车挡风玻璃外雨刮器的运动属于平移现象．19．树上的水果掉在地上，是平移现象．．20．轴对称图形的两个对称点到对称轴的距离相等．．四．操作题（满分24分，每小题6分）21．（6分）下面哪个图案是由通过平移拼成的？把它涂上颜色。

7.1轴对称图形一、填空。

1、如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是（），折痕所在的直线叫做（）。

2、圆的对称轴有（）条，半圆形的对称轴有（）条。

3、（）三角形有三条对称轴，（）三角形有一条对称轴。

4、正方形有（）条对称轴，长方形有（）条对称轴，等腰梯形有（）条对称轴。

二、选择题。

1、下列英文字母中，是轴对称图形的是（）A、SB、HC、PD、Q2、下列图形中：角、线段、直角三角形、等边三角形、长方形，其中一定是轴对称图形的有（）A、2个B、3个C、4个D、5个3、下列图形中，对称轴最多的是（）。

A、等边三角形 B 、正方形 C 、圆 D、长方形4、下面不是轴对称图形的是（）。

A、长方形B、平行四边形C、圆D、半圆三、操作题：1、试找出如图所示的每个正多边形的对称轴的条数，并填下表格中．正多边形的边数 3 4 5 6 7 8对称轴的条数7.2图形的平移一、将图中的小船向左平移5格。

二、画一画：梯形先向下平移2格，再向左平移7格。

三、你能把小亭子图从左上方平移到右下方吗？想一想，有几种方法能实现。

四、画一画。

1. 平行四边形先向右平移5格，再向上平移4格。

2. 梯形先向下平移2格，再向左平移7格。

7.1 轴对称图形1.仔细观察,下列哪些图案是轴对称图形?是的,画出对称轴。

2.在下面图形中,你还能画出其他对称轴吗?如果能,请画出来并填空。

()条对称轴()条对称轴()条对称轴()条对称轴()条对称轴3.分别画出下面图形的另一半,使它成为一个轴对称图形。

7.2 练习二十1.填一填。

(1)点A到对称轴的距离是()格,点A'到对称轴的距离是()格。

(2)点B到对称轴的距离是()格,点B'到对称轴的距离是()格。

2.画出轴对称图形的另一半。

3.在下图中补画一个同样大小的正方形,使整个图形成为轴对称图形。

7.3 画出平移后的图形1.数一数,房子向()平移()格。

2.小鱼向( )平移了( )格。

第七单元图形的运动（二）-四年级数学下册易错点汇总及优选易错题B卷本单元知识点易错汇总：1. 对称轴是一条直线。

射线、线段都不能称为图形的对称轴。

2. 轴对称图形中连接对称点的线段一定垂直于对称轴并被对称轴平分。

3. 轴对称图形被对称轴分成的两部分沿对称轴对折后能够完全重合。

4. 图形平移的距离是指对应点之间的距离，而不是指两个图形之间空格的距离。

5. 在对图形进行两次平移时，一定要正确理解题意，明确平移的顺序、方向和距离。

6. 把不规则图形转化为规则图形的方法往往不止一种。

（时间：60分钟，总分：100分）一．选择题（满分16分，每小题2分）1．图案可以从()中剪出来。

A．B．C．2．下列各组图形中能通过平移得到是()A．B．C．D．3．下列现象是平移的是()A．钟表的时针移动B．轮子的滚动C．抽屉的进出滑动D．电风扇的转动4．下面属于平移现象的是()A．拧开瓶盖B．旋转门C．直升电梯5．如图，图()是平移现象．A．①B．②C．③D．④6．从镜子中看到现在是4时，正确的时间是()A．4时B．8时C．2时7．下图中，BC的长度是6厘米，点B到对称轴的距离是()厘米．A．3厘米B．4厘米C．6厘米D．12厘米8．如图，将一张长方形纸对折，并剪下一个三角形和一个圆，余下的部分展开后的形状是( )A．B．C．二．填空题（满分16分，每小题2分）9．如果两个图形关于某一直线对称，那么它们的对称轴是连接两个对应点所得的线段的。

10．你见过这些现象吗？这两幅图的内容是对称。

11．在轴对称图形中，对称轴两侧相对应的点到对称轴的距离。

12．平移作图时，要找准平移方向，还要数清平移的。

13．如果在平面镜中看到一辆汽车的车牌号是：，那么该汽车的车牌号码是．14．星期日，小黄在家要练书法。

开始时，他从镜子里看了一下钟；写完后，他又从镜子里看了一下钟（如图）。

他这次练书法一共用的时间是。

15．生活中见到的平移现象有、、。

人教版四年级数学下册第七单元《图形的运动二》知识点第七单元知识点
1、把一个图形沿着某一条直线对折，如果直线两旁的部分能够完全重合，我们就说这个图形是轴对称图形，这条直线叫做这个图形的对称轴。

2、轴对称的性质：对应点到对称轴的距离都相等。

3、对称轴是一条直线，所以在画对称轴时，要画到图形外面，且要用虚线。

4、正方形的对角线所在的直线是它的对称轴。

轴对称图形可以有一条或几条对称轴。

5、画对称轴时，先找到与相反方向距离对称轴相同的对应点，最后连线。

6、长方形、正方形、等腰梯形、等腰三角形、等边三角形、线段、菱形都是轴对称图形。

长方形有2条对称轴，
正方形有4条对称轴，
等腰梯形有1条对称轴，
等腰三角形有一条对称轴，
等边三角形有3条对称轴，
线段有1条对称轴，
菱形有2条对称轴，
圆有无数条对称轴，
半圆有一条，
圆环有无数条，
半圆环有一条。

7、平行四边形不是轴对称图形，没有对称轴。

（长方形和正方形除外）
8、梯形不一定是轴对称图形。

只有等腰梯形是轴对称图形。

9、古今中外，许多著名的建筑就是对称的。

比如：中国的赵州桥，印度泰姬陵，英国塔桥，法国埃菲尔铁塔。

10、平移先找图形点，平移完点连起来，注意数点数要数十字。

11、平移不改变图形的大小、形状，只改变图形的位置。

12、利用平移，可以求出不规则图形的面积。

人教版四年级图形的运动知识点归纳以及练习题work Information Technology Company.2020YEAR1.轴对称（1）轴对称图形的定义如果一个平面图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴（2）轴对称图形的基本性质对应点到对称轴的距离相等，对称的两部分的大小相等，形状相同，只是方向相反。

（3）补全一个轴对称图形的方法①确定已知图形的关键点，如图形的顶点，交点，端点等②数出或量出关键点到对称轴的距离③在对称轴的另一侧描出关键点的对应点④按照已知那一般图形的形状顺次连接各赌赢点，把轴对称图形补充完整练习：1.画对称轴画出下列图形的对称轴画对称轴时要注意，该图形有几条对称轴就画出来几条2.补全轴对称图形3.长方形有（）条对称轴，正方形有（）条对称轴，圆有（）条对称轴4.把一张长方形纸片折叠，使BC边落在FE处，折痕为GH，梯形AGHD和梯形GHEF的面积分别是25cm²和20cm²，原长方形的面积是多少？2.平移（1）平移的含义一个简单的物体按照一定的方向（向上或向下或向左或向右）和距离从一个位置移动到另一个位置，这个构成叫做平移平移后的图形与平移前的图形大小相等，形状相同，只是所在位置发生了变化（2）画出平移后的图形的方法①要确定平移的图形的关键的点②确定平移的方向和长度③描出关键定平移后的对应点，按照已知图形的形状顺次连接各对应点，即可画出平移后的图形（3）通过切割---平移---填补的方法解决实际问题练习：1.分别画出将图形向上平移四个格，再向右平移12个格，最后向下平移7个格的图形2.求下列图形的面积：3.画出下列轴对称图形的另一半，并画出这个轴对称图形向左平移16个格，在向下平移6个格后得到的图形4.求下图的面积：5.你能算出，一只蚂蚁从这个楼梯爬一次所经过的路程有多少米吗？6.下面是一个椭圆形公园的平面图，中间有一个圆形的游泳池，求这个公园的陆地面积7.如图，某小区有一块长为42m、宽22m的长方形草坪，先要在草坪里铺设一横两纵三条等宽的甬道，已知每条甬道的宽度都是2m，求铺设甬道后草坪的面积。

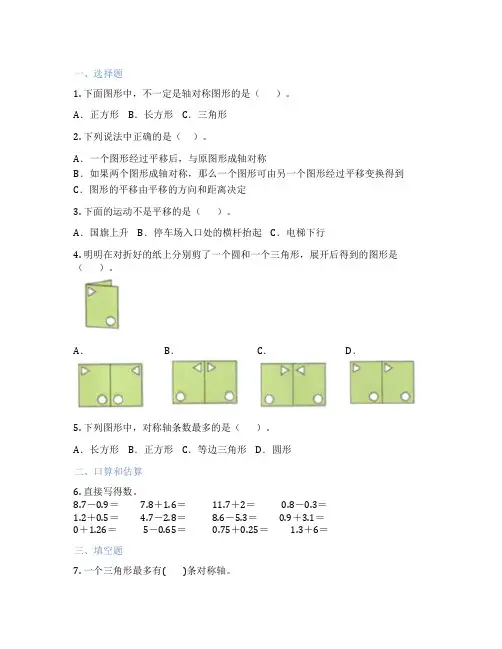
一、选择题1. 下面图形中，不一定是轴对称图形的是（）。

A．正方形B．长方形C．三角形2. 下列说法中正确的是（）。

A．一个图形经过平移后，与原图形成轴对称B．如果两个图形成轴对称，那么一个图形可由另一个图形经过平移变换得到C．图形的平移由平移的方向和距离决定3. 下面的运动不是平移的是（）。

A．国旗上升B．停车场入口处的横杆抬起C．电梯下行4. 明明在对折好的纸上分别剪了一个圆和一个三角形，展开后得到的图形是（）。

A．B．C．D．5. 下列图形中，对称轴条数最多的是（）。

A．长方形B．正方形C．等边三角形D．圆形二、口算和估算6. 直接写得数。

8.7－0.9＝ 7.8＋1.6＝ 11.7＋2＝ 0.8－0.3＝1.2＋0.5＝ 4.7－2.8＝ 8.6－5.3＝ 0.9＋3.1＝0＋1.26＝ 5－0.65＝ 0.75＋0.25＝ 1.3＋6＝三、填空题7. 一个三角形最多有( )条对称轴。

8. 平移图形时要注意移动的方向和_____．9. 下图是由4个边长是2分米的正方形拼成的图形，图中阴影部分的面积是( )平方分米。

10. 沿一条直线将某一图形对折后，两部分能完全重合，我们把这种图形叫( )图形，折痕所在的直线叫做( )。

11. 看图回答（1）房子图先向________平移了________格，再向________平移了________格．（2）松树图先向________平移了________格，再向________平移了________格．四、解答题12. 如图，菜地中间的小路宽1米，实际种菜的面积是多少？13. 按要求在方格纸上画图。

（1）根据对称轴补全下面的轴对称图形。

（2）画出将轴对称图形向右平移9格后的图形。

（3）如果每个方格表示1cm2，这个轴对称图形的面积是（）cm2。

14. 一块长方形草地长，宽，中间有两条小路（如下图）。

这两条小路的总面积是多少？现在要给这两条小路铺上一层鹅卵石，平均每平方米约需鹅卵石，大约共需多少千克鹅卵石？15. 如图，根据图中对称轴，补全图形A的另一半，并计算的周长。

小学数学图形的运动知识点总结1．圆与组合图形【知识点归纳】1．圆知识的相关回顾：（1）圆的周长C＝2πr＝或C＝πd（2）圆的面积S＝πr2（3）扇形弧长L＝圆心角（弧度制）×r＝（n为圆心角）（4）扇形面积S＝＝（L为扇形的弧长）（5）圆的直径d＝2r2．组合图形的面积计算，可以根据几何图形的特征，通过分割、割补、平移、翻折、对称、旋转等方法，化复杂为简单，变组合图形为基本图形的加减组合．2．组合图形的面积【知识点归纳】方法：①“割法”：观察图形，把图形进行分割成容易求得的图形，再进行相加减．②“补法”：观察图形，给图形补上一部分，形成一个容易求得的图形，再进行相加减．③“割补结合”：观察图形，把图形分割，再进行移补，形成一个容易求得的图形．【命题方向】常考题型：例1：求图中阴影部分的面积．（单位：厘米）分析：根据图所示，可把组合图形分成一个直角梯形和一个圆，阴影部分的面积等于梯形的面积减去圆的面积再加上圆的面积减去三角形面积的差，列式解答即可得到答案．解：[（5+8+5）×5÷2﹣×3.14×52]+（×3.14×52﹣5×5÷2），＝[18×5÷2﹣0.785×25]+（0.785×25﹣25÷2），＝[90÷2﹣19.625]+（19.625﹣12.5），＝[45﹣19.625]+7.125，＝25.375+7.125，＝32.5（平方厘米）；答：阴影部分的面积为32.5平方厘米．点评：此题主要考查的是梯形的面积公式（上底+下底）×高÷2、三角形的面积公式底×高÷2和圆的面积公式S＝πr2的应用．3．轴对称【知识点归纳】1．轴对称的性质：像窗花一样，把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，称这两个图形为轴对称，这条直线叫做对称轴，两个图形中的对应点叫做对称点．把一个图形沿着某一条直线折叠，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴．2．性质：（1）成轴对称的两个图形全等；（2）如果两个图形成轴对称，那么对称轴是对称点连线的垂直平分线．【命题方向】常考题型：例：如果把一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形．分析：依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，据此即可进行解答．解：据分析可知：如果把一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形．故答案为：一条直线、完全重合、轴对称图形．点评：此题主要考查轴对称图形的意义．4．确定轴对称图形的对称轴条数及位置【知识点归纳】1．对称轴的定义：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线（成轴）对称，这条直线就是它的对称轴．2．找到对应点的连线，如果连线的中点都在一条直线上，说明是其图形的对称轴．3．掌握一般图形的对称轴数目和位置对于快速判断至关重要．【命题方向】常考题型：例：下列图形中，（）的对称轴最多．A、正方形B、等边三角形C、等腰三角形D、圆形分析：依据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线就是其对称轴，从而可以作出正确选择．解：（1）因为正方形沿两组对边的中线及其对角线对折，对折后的两部分都能完全重合，则正方形是轴对称图形，两组对边的中线及其对角线就是其对称轴，所以正方形有4条对称轴；（2）因为等边三角形分别沿三条边的中线所在的直线对折，对折后的两部分都能完全重合，则等边三角形是轴对称图形，三条边的中线所在的直线就是对称轴，所以等边三角形有3条对称轴；（3）因为等腰梯形沿上底与下底的中点的连线对折，对折后的两部分都能完全重合，则等腰梯形是轴对称图形，上底与下底的中点的连线就是其对称轴，所以等腰梯形有1条对称轴；（4）因为圆沿任意一条直径所在的直线对折，对折后的两部分都能完全重合，则圆是轴对称图形，任意一条直径所在的直线就是圆的对称轴，所以说圆有无数条对称轴．所以说圆的对称轴最多．故选：D．点评：解答此题的主要依据是：轴对称图形的概念及特征．例2：下列图形中，对称轴条数最多的是（）分析：先找出对称轴，从而得出对称轴最多的图形．解：A：根据它的组合特点，它有4条对称轴；B：这是一个正八边形，有8条对称轴；C：这个组合图形有3条对称轴；D：这个图形有5条对称轴；故选：B．点评：此题考查了轴对称图形的定义，要求学生能够正确找出轴对称图形的对称轴．5．轴对称图形的辨识【知识点归纳】1．轴对称图形的概念：如果一个图形沿着一条直线对折，直线两边的图形能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．2．学过的图形中，线段、角、等腰三角形、等边三角形、长方形、正方形、等腰梯形、圆形、扇形都是轴对称图形，各自有不同数目的对称轴．【命题方向】常考题型：例：如图的交通标志中，轴对称图形有（）A、4B、3C、2D、1分析：依据轴对称图形的定义即可作答．解：图①、③沿一条直线对折后，直线两旁的部分能够互相重合，所以图①、③是轴对称图形；图②、④无论沿哪一条直线对折后，直线两旁的部分都不能够互相重合，所以它们不是轴对称图形．如图的交通标志中，轴对称图形有2个．故选：C．点评：此题主要考查轴对称图形的定义．6．作轴对称图形【知识点归纳】1．如果一个图形沿着一条直线对折，直线两边的图形能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．2．学过的图形中，线段、角、等腰三角形、等边三角形、长方形、正方形、等腰梯形、圆形、扇形都是轴对称图形，各自有不同数目的对称轴．通过以上图形的组合就可以得到轴对称图形了．【命题方向】常考题型：例：（1）画出图A的另一半，使它成为一个轴对称图形．（2）把图B向右平移4格．（3）把图C绕O点顺时针旋转180°．分析：（1）根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的下边画出图形A的关键对称点，连结涂色即可．（2）根据平移的特征，把图形B的各点分别向右平移4格，再依次连结、涂色即可．（3）根据旋转图形的特征，图形C绕点O顺时针旋转180°，点O的位置不动，其余各部分均绕点O按相同的方向旋转相同的度数即可画出旋转后的图形．解：（1）画出图A的另一半，使它成为一个轴对称图形（下图）．（2）把图B向右平移4格（下图）．（3）把图C绕O点顺时针旋转180°（下图）．点评：此题是考查作轴对称图形、作平移的图形、作旋转图形．关键是确定对称点（对应点）的位置．7．平移【知识点归纳】1．平移：把一个图形整体沿某一方向移动一定的距离，图形的这种移动，叫做平移．2．平移后图形的位置改变，形状、大小不变．【命题方向】常考题型：例：电梯上升是（）现象．A、旋转B、平移C、翻折D、对称分析：平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动．电梯的升降是上下位置的平行移动所以是平移，据此解答判断．解：电梯的升降是上下位置的平行移动，所以电梯的升降是平移现象；故选：B．点评：本题主要考查平移的意义，在实际当中的运用．8．作平移后的图形【知识点归纳】1．确定平移后图形的基本要素有两个：平移方向、平移距离．2．作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．【命题方向】常考题型：例：分别画出将向上平移3格、向右平移8格后得到的图形．分析：根据平移图形的特征，把平行四边形A的四个顶点分别向上平移3格，再首尾连结各点，即可得到平行四边形A向上平移3格的平行四边形B；同理，把平行四边形B的四个顶点分别向右平移8格，再首尾连结各点，即可得到平行四边形B向右平移8格的平行四边形C．解：作平移后的图形如下：点评：作平移后的图形关键是把对应点的位置画正确．。

加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好! 经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！1四年级数学下册典型例题系列之第七单元图形的运动（二）（解析版）编者的话：《四年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题和专项练习两大部分。

典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

本专题是第七单元图形的运动（二）。

本部分内容主要考察轴对称的认识及作图和平移的认识及作图，题型相对简单，多为作图题，一共划分为十二个考点，建议作为本章重点内容进行讲解，欢迎使用。

人教版小学数学图形的运动知识点汇总一、知识要点(一)合同运动一-平移、旋转和轴对称1.平移。

(1)概念及特征。

在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。

平移只改变图形的位置，不改变图形的大小和形状。

(2)画法。

①选点：在原图形上选择几个能决定图形形状和大小的点。

②移点：按要求把选择的点向规定的方向平移规定的格数。

③连点成形。

2.旋转。

(1)概念及特征在平面内，将一个图形绕一点沿某个方向转动一个角度，这样的图形运动称为旋转。

旋转只改变图形的位置，不改变图形的形状和大小。

(2)画法。

（以图形绕某一点旋转90°为例）①确定旋转中心和旋转方向。

②找到原图形中关健点绕旋转中心旋转90°后的对应点。

③连点成形。

3.轴对称。

(1)概念及特征。

如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形。

折痕所在的这条直线叫对称轴。

线段、角、等腰三角形、长方形、正方形、圆、扇形等都是轴对称图形，它们的对称轴条数如下：正方形有4条对称轴，长方形有2条对称轴，等腰三角形有1条对称轴，等边三角形有3条对称轴，等腰梯形有1条对称轴，圆有无数条对称轴，扇形有1条对称轴。

(2)补全轴对称图形的方法。

①“找”：找出图形上每条线段的端点。

②“定”：根据对称轴确定每一个端点的对称点。

③“连”：依次连接这些对称点，得到轴对称图形的另一半。

(二)相似运动一图形的放大与缩小1.特征。

将图形按一定的比放大或缩小，是图形变换的一种方式，它只改变图形的大小，而不改变图形的形状。

2.画放大或缩小后图形的方法。

将一个图形按指定的比放大或缩小，首先要看清楚是按什么样的比进行变换，然后选取原图形中关键的一些线段，按指定的比放大或缩小（也就是要注意原图形的各边均要用相同的比来放大或缩小)，注意不能改变图形的形状。

四年级下数学《图形的运动》知识点总结归纳
一、基本概念
1.图形运动：图形在平面内按照某种规律或路径进行移动，但不发生翻转或变形。

2.平移：图形在平面内沿某一方向直线移动一定的距离，不发生旋转。

3.旋转：图形围绕某一点转动一定的角度，不发生移动。

二、平移性质
1.平移不改变图形的形状、大小和方向。

2.平移后，对应点所连的线段与平移方向平行且等长。

3.平移后，对应线段平行且等长，对应角相等。

三、旋转性质
1.旋转不改变图形的形状、大小和方向。

2.旋转后，对应点到旋转中心的距离相等，对应线段相等，对应角相等。

3.旋转后，图形上对应点到旋转中心的距离等于旋转半径，对应线段与旋转半径
相等，旋转中心到图形上任意一点的距离都是相等的。

四、平移与旋转的区别与联系
1.区别：平移是沿某一方向直线移动一定的距离；旋转是围绕某一点转动一定的
角度。

2.联系：平移可以看作是旋转（围绕某一点）在直线上的表现形式；旋转也可以
看作是平移（沿某一方向）在圆周上的表现形式。

五、图形运动的实例
1.平移实例：火车在铁轨上行驶、电梯上下移动、推拉门等。

2.旋转实例：风力发电机叶片的转动、车轮的转动、旋转木马等。

通过本节课的学习，学生将了解图形运动的基本概念和平移、旋转的性质，掌握图形运动的基本规律，并能够在实际生活中应用这些知识解决一些实际问题。

图形的运动（二）第1课时轴对称基础导学练知识点1 轴对称图形的基本性质1．下面图形是轴对称图形的在括号里打“√”。

（）（）（）（）（）（）（）（）2．填空。

（1）在轴对称图形中，对称点的连线与对称轴( )，对称点到对称轴的距离( )。

（2）在长方形、正方形、三角形中，一定是轴对称图形的是( )，不一定是轴对称图形的是( )。

知识点2 画一个图形的轴对称图形或一个轴对称的另一半3．以虚线为对称轴，画出下面各图形的对称图形。

4．在方格纸上画出轴对称图形的另一半。

（图中虚线为对称轴）易错点对轴对称图形的性质理解不透而导致误判5．判断。

（1）长方形是轴对称图形，它有4条对称轴。

（）（2）平行四边形一定是轴对称图形。

（）应用提升练提升点1 画出图形的对称轴6．画出下面图形的所有对称轴。

提升点2 以格子图的对角线为对称轴画轴对称图形的另一半7．画出轴对称图形的另一半（以虚线为对称轴）。

思维导学练8．如图，将下面正方形分成四块面积相等的图形，并且整个图形是轴对称图形，你能想出几种分法？画一画例如：第2课时图形的平移基础导学练知识点1 确定平移的方向和距离1．下面图形中，图( )是图A平移得到的。

2．看图填空。

(3)由图A绕点N按顺时针方向旋转90°得到图B。

( )图形①向( )平移了( )格；图形②向( )平移了( )格；图形③向( )平移了( )格。

知识点2 在方格纸上按要求画出平移后的图形3．画一画。

（1）画出三角形向右平移4格后的图形。

（2）画出平行四边形向下平移3格后的图形。

（3）画出大树向右平移2格，再向下平移1格后的图形。

易错点没有正确掌握平移的特点导致画图错误4．下面的画法对吗？若不对，那是平移了多少格？将三角形向右平移4格。

应用提升练提升点利用“观察法”和“平移法’解决平移问题5．先根据对称轴（图中的虚线）补全轴对称图形，再画出这个轴对称图形向左平移7格后的图形。

思维拓展练6．图形(1)怎样拆分平移能得到图形(2)?第3课时运用平移知识解决面积问题基础导学练知识点1 运用平移解决问题1．先移一移，再看阴影部分占整个图形的几分之几。

人教版小学四年级数学下册同步复习与测试讲义第七章图形的运动（二）【知识点归纳总结】1.轴对称1．轴对称的性质：像窗花一样，把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，称这两个图形为轴对称，这条直线叫做对称轴，两个图形中的对应点叫做对称点．把一个图形沿着某一条直线折叠，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴．2．性质：（1）成轴对称的两个图形全等；（2）如果两个图形成轴对称，那么对称轴是对称点连线的垂直平分线．【经典例题】例：如果把一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形．分析：依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，据此即可进行解答．解：据分析可知：如果把一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是轴对称图形．故答案为：一条直线、完全重合、轴对称图形．点评：此题主要考查轴对称图形的意义．2.镜面对称1．镜面对称：有时我们把轴对称也称为镜面（镜子、镜像）对称，如果沿着图形的对称轴上放一面镜子，那么在镜子里所放映出来的一半正好把图补成完整的（和原来的图形一样）．2．将镜面看做对称轴，那么关于镜面对称的像关于对称轴对称．【经典例题】例：如图是小明在镜子中看到的钟表的图象，他表示的真实时间是（）A、4：40B、4：20C、7：20D、7：40分析：根据镜面对称的性质，在平面镜中的像与现实中的事物恰好左右颠倒，且关于镜面对称，分析并作答．解：根据镜面对称的性质，分析可得题中所显示的时刻与4：40成轴对称，所以此时实际时刻为4：40；故选：A．点评：本题考查镜面反射的原理与性质．解决此类题应认真观察，注意技巧．3.平移1．平移：把一个图形整体沿某一方向移动一定的距离，图形的这种移动，叫做平移．2．平移后图形的位置改变，形状、大小不变．【经典例题】例：电梯上升是（）现象．A、旋转B、平移C、翻折D、对称分析：平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动．电梯的升降是上下位置的平行移动所以是平移，据此解答判断．解：电梯的升降是上下位置的平行移动，所以电梯的升降是平移现象；故选：B．点评：本题主要考查平移的意义，在实际当中的运用．【同步测试】单元同步测试题一．选择题（共10小题）1．下图中，BC的长度是6厘米，点B到对称轴的距离是（）厘米．A．3厘米B．4厘米C．6厘米D．12厘米2．补全轴对称图形的时候，要先找到（）A．边界B．对称轴C．端点3．从镜子中看到现在是4时，正确的时间是（）A．4时B．8时C．2时4．如图从镜子中看到的图形是（）A．B．C．5．下列哪种现象属于平移（）A．荡秋千B．乘坐电梯C．翻书6．小红在镜子里看到墙上的挂钟如图所示，请问第（）个时间最接近8：00．A．B．C．D．7．是从（）上剪下来的．A．B．C．D．8．如图是小明在平面镜中看到时钟形成的像，它的实际时间是（）A．21：05B．12：02C．12：05D．15：029．下列图（）是由如图平移得到的．A．B．C．D10．笑笑非常喜爱《小英雄雨来》中“我们是中国人，我们爱自己的祖国”这句话，于是她自己刻了一枚如左图所示的印章．下面四个图案中用这枚印章印制的是（）A．B．C．D．二．填空题（共8小题）11．如图的钟面是从镜子里看到的，实际钟面上的时刻是．12．如图，由图A到图B是向平移了格，由图B到图C是向平移了格．13．拨动算盘是现象．14．一个图形对折后，两边能够完全，这个图形是，这条折痕所在的直线叫做．15．在一幅轴对称图形中，沿对称轴对折后A点与B点重合．如果A点到对称轴的距离是4厘米，那么未对折前A点到B点的距离是厘米．16．在平面镜里看到背后墙上，电子钟示数如图所示，这时的时间应是．17．小明在镜子中看到钟面上是4：30，实际钟面上是．18．被列为非物质文化遗产的陕北剪纸，通过现场操作等多种形式，让市民体验到了传统技艺的妙趣．某市民将一个正方形彩纸依次按如图1、图2所示的方式对折，然后沿图3中的虚线裁剪，则将图3的彩纸展开铺平后的图形是图4中的．（填序号）三．判断题（共5小题）19．两个圆组成的图形一定是轴对称图形．（判断对错）20．是轴对称图形．（判断对错）21．平移改变了图形的位置，形状和大小．（判断对错）22．从镜子中看到左图的样子是这样的．．（判断对错）23．淘气举左手时，镜子中的淘气举右手．．（判断对错）四．操作题（共2小题）24．如图，图形①经过怎样的运动可以得到图形②？25．下面的图案各是从哪张纸上剪下来的？请连线．五．解答题（共3小题）26．看图填空①（1）向平移了格．②（2）向平移了格．③（3）向平移了格．27．请你用三种不同的方法分别图中添画一个小正方形，使它成为一个轴对称图形．28．从镜子中看到的左边图形的样子是什么？请在认为正确的图形上画“√”．参考答案与试题解析一．选择题（共10小题）1．【分析】依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，对称点到对称轴的距离相等，所以BC的长度是6厘米，点B到对称轴的距离是6÷2＝3（厘米）；据此即可进行解答．【解答】解：因为对称点到对称轴的距离相等，所以，BC的长度是6厘米，点B到对称轴的距离是6÷2＝3（厘米）．故选：A．【点评】此题主要考查轴对称图形的意义以及对称轴的性质运用．2．【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在补全轴对称图形的时候，首先在对称轴的另一边画出原图的关键对称点，然后依次连结即可完成轴对称图形．据此解答．【解答】解：由分析得：在补全轴对称图形的时候，首先在对称轴的另一边画出原图的关键对称点，然后依次连结即可完成轴对称图形．故选：C．【点评】此题考查的目的是理解掌握轴对称图形的特征及应用．3．【分析】根据镜面对称的性质求解，在平面镜中的像与现实中的事物恰好左右顺序颠倒，且关于镜面对称．【解答】解：从镜子中看到现在是4时，正确的时间是8时；故选：B．【点评】本题是考查镜面对称，白镜面对称的特点是：上下前后方向一致，左右方向相反．4．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：如图故选：B．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．5．【分析】把一个图形整体沿某一方向移动一定的距离，图形的这种移动，叫做平移．根据平移不改变图形的形状、大小和方向，结合图形对选项进行一一分析，选出正确答案．【解答】解：荡秋千、翻书，运动过程中改变了方向，不符合平移的性质；乘坐电梯，符合平移的性质，故属于平移；故选：B．【点评】本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．6．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称，我们画出这几个钟面所表示的时刻，即可得知第几个时间最接近8：00．【解答】解：如图，图A与8：00相差5分，图B与8：00相差30分，图C和图D与8：00相差3小时45分，最接近8：00的时图A．故选：A．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．7．【分析】作出这个图形的纵向对称轴，看左侧与下面哪个图形的空缺部分相吻合，就是从哪个图形上剪下来的．【解答】解：如图故选：C．【点评】把一张纸对折后，在对折边处剪出的图形是以纸的折痕为对称轴的轴对称图形．8．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：如图实际时间是12：05．故选：C．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．9．【分析】图形平移后，只是位置的变化，图形大小、形状、方向不变．A图、B图、D图大小没变，但方向变了，不是原图平移后得到的；C图大小、形状、方向没变，是原图平移后的图形．【解答】解：经过平移后得到即图形C是由原图平移得到的．故选：C．【点评】关键抓住平移的特征：图形平移后，只是位置的变化，图形大小、形状、方向不变．10．【分析】印章与印出的图案如同镜面对称，根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称，也就是印章与印出的图案上、下一致，左右方向相反，大小不变．【解答】解：如图，故选：B．【点评】关键明白印章与印出的图案如同镜面对称，根据镜面对称原理进行选择．二．填空题（共8小题）11．【分析】镜面对称的特点是：上下前后方向一致，左右方向相反；图中镜子里看到的时间是6：40，由镜面对称左右方向相反特点，镜中时针在6与7之间，实际是在5与6之间，是5时，镜中分针指刻度8，实际中是指刻度4，即20分；据此解答．【解答】解：因为镜中时针在6与7之间，实际是在5与6之间，是5时，镜中分针指着刻度8，实际中是指刻度4，即20分，所以实际钟面上的时刻是5：20．故答案为：5：20．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反．12．【分析】根据图中两图的相对距离及箭头指向即可确定平移的方向和距离，所以图A到图B是向右平移了6格，由图B到图C是向下平移了2格；由此解答即可．【解答】解：如图，由图A到图B是向右平移了6格，由图B到图C是向下平移了2格．故答案为：右，6，下，2．【点评】作图形平移要注意三要素：即原位置、平移方向、平移距离．13．【分析】平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动．拨动算盘是上下位置的平行移动，据此解答．【解答】解：拨动算盘是上下位置的平行移动，所以拨动算盘是平移现象．故答案为：平移．【点评】本题主要考查平移的意义，在实际当中的运用．14．【分析】依据轴对称图形的定义即可作答．一个图形沿着某一条直线折叠，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴．【解答】解：一个图形对折后，两边能够完全重合，这个图形是轴对称图形，这条折痕所在的直线叫做对称轴．答案为；重合，轴对称图形，对称轴．【点评】此题主要考查轴对称图形的定义．15．【分析】依据轴对称图形的特点，即轴对称图形是指一个图形沿一条直线折叠后直线两旁的部分能够完全重合，这条直线就是这个轴对称图形的对称轴．轴对称图形中，对称点到对称轴的距离相等．【解答】解：4×2＝8（厘米）答：如果A点到对称轴的距离是4厘米，那么未对折前A点到B点的距离是8厘米．故答案为：8．【点评】此题主要考查轴对称图形的特点．16．【分析】根据镜面对称的性质，在平面镜中的像与现实中的事物恰好左右颠倒，且关于镜面对称，分析并作答．【解答】解：根据镜面对称的性质，分析可得题中所显示的时刻与21：05成轴对称，所以此时实际时刻为21：05．故答案为：21：05．【点评】本题考查镜面反射的原理与性质．解决此类题应认真观察，注意技巧．17．【分析】根据镜面对称的性质求解，在平面镜中的像与现实中的事物恰好左右相反，且关于镜面对称．【解答】解：根据镜面对称的性质，题中所显示的时刻成轴对称，所以此时实际时刻为7：30．故答案为：7：30．【点评】本题考查镜面反射的原理与性质．解决此类题应认真观察，注意技巧．18．【分析】找一张纸，按照图中的顺序向上对折，再向左对折，按位置剪去画的虚线的形状，然后展开即可．【解答】解：经过动手操作，发现将图3的彩纸展开铺平后的图形是图4中的第四个图．故答案为：④．【点评】此题主要考查轴对称图形的意义和动手操作的能力．三．判断题（共5小题）19．【分析】两个圆无论半径相等，还是不相等，无论是相交、相切或相离、还是内含，组成的图形都是轴对称图形，只对称轴的条数多少而已，最多是两个圆组成环形，有无数条对称轴，最少有一条对称轴．【解答】解：两个圆组成的图形一定是轴对称图形原题说法正确．故答案为：√．【点评】无论两个圆的大小如何，位置关系怎样，所组成的图形一定是轴对称图形．20．【分析】根据对称轴的定义：如果一个图形沿着一条直线对折，两侧的图形能完全重合，这个图形就是轴对称图形．折痕所在的这条直线叫做对称轴，据此即可进行判断．【解答】解：根据轴对称图形的意义可知：是轴对称图形，说法正确；故答案为：√．【点评】解答此题的主要依据是：轴对称图形的意义及特征．21．【分析】平移是指在平面内，将一个图形上的所有点都按照某个方向作相同距离的移动．平移不改变图形的形状和大小，只是改变位置；把一个图形绕着某一点转动一个角度的图形变换叫做旋转，旋转时图形位置发生变化，大小不变，形状不变．【解答】解：平移只改变了图形的位置，没有改变图形的形状，故原题说法错误；故答案为：×．【点评】本题是考查平移的特点、旋转的特点．旋转与平移的相同点：位置发生变化，大小不变，形状不变，都在一个平面内．不同点：平移，运动方向不变．旋转，围绕一个点或轴，做圆周运动．22．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．【解答】解：从镜子中看到左图的样子是这样的．故答案为：×．【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．23．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：如图淘气举左手时，镜子中的淘气举右手．原题的说法是正确的．【点评】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．四．操作题（共2小题）24．【分析】据平移的意义“平移是指在同一平面内，将一个图形整体按照某个直线方向移动一定的距离，这样的图形运动叫作图形的平移运动，简称平移”，由此可知：把图①向下平移4格再向右平移5格即可得到图②；由此解答即可．【解答】解：根据平移的性质可知：把图①向下平移4格再向右平移5格即可得到图②．【点评】本题是考查平移图形的特征，平移和旋转不改变图形的形状和大小，平移不改变图形的方向，旋转则改变图形的方向．25．【分析】图案左起第一个和第二个不同，每个花瓣上有凹陷第二个没有，第二个有柄，第一个没有，第三个是心型，第四个是葫芦型，第一个连第二行的左起第三个，每二个连每四个，第三个连第一个，第四个连第二个．【解答】解：根据分析连线如下：【点评】本题是考查图形的组拼，相似的要注意观察细微部位．五．解答题（共3小题）26．【分析】把一个图形整体沿某一方向移动一定的距离，图形的这种移动，叫做平移，据此解答即可．【解答】解：①（1）向上平移了2格．②（2）向左平移了4格．③（3）向右平移了6格．故答案为：上，2，左，4，右，6．【点评】本题是考查作平移后的图形，注意，一看方向（左、右、上、下），二看对应点（或边）距离几格．27．【分析】依据轴对称图形的含义，即在平面内，如果一个图形沿一条直线对折，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，据此即可完成作图．【解答】解：如图所示，即为所要求的画图：【点评】解答此题的主要依据是：轴对称图形的意义及特征．28．【分析】根据镜面对称的特征，镜中的景物与实际景物上下前后方向一致，左右方向相反，大小不变，且关于镜面对称．【解答】解：根据镜面对称，如下图：【点评】此题主要明白镜面对称的特点是：上下前后方向一致，左右方向相反，镜中与实际景物大小不变．。

人教版四年级数学下册第7单元《图形的运动》知识点梳理一、轴对称1.轴对称图形的意义:将图形沿一条直线对折,如果直线两侧的部分能够完全重合,这样的图形叫做轴对称图形,折痕所在的这条直线叫做它的对称轴。

对称轴是一条直线．．．．．．．．．．．．．．．．．．．．．．．．,．不能称射线、线段为图形的对称轴。

2.轴对称图形的基本性质:对应点到对称轴的距离相等。

3.轴对称图形的特征:沿对称轴对折,对应点重合。

4.补全一个轴对称图形的方法。

(1)定点．．:确定已知图形的关键点,如图形的顶点、相交点、端点等。

(2)数格．．:数出关键点到对称轴的距离。

(3)描点．．:在对称轴的另一侧描出关键点的对应点。

(4)连线．．:按照已知图形的形状顺次连接各对应点,补全这个轴对称图形。

如:画出轴对称图形的另一半。

注意:(．1．)．轴对称图形中连接对应点的线段一定垂直于对称轴．．．．．．．．．．．．．．．．．．．．．．．．,．并被对称轴平分。

．．．．．．(．2．)．轴对称图形被对称轴分成的两部分．．．．．．．．．．．．．．．．．．．．．．．．．．,．沿对称轴对折后能够完全重合。

．．．二、平移1.平移的意义:在平面内,将一个图形沿着某一个方向移动一定的距离,这样的图形运动叫做平移。

2.平移的特点．．．．．:．不改变物体的形状和大小．．．．．．．．．．．,．只改变物体的位置。

．．．．．．．．．3.平移的两个要素:方向和距离。

．．．．．．4.确定方格中图形平移的方向和距离的方法。

(1)根据箭头的指向能够确定平移的方向。

(2)找出平移前后两个图形的一组对应点,对应点之间的距离就是图形平移的距离。

5.平移后的图形的画法。

(1)选点．．:在原图上选几个能决定图形形状和大小的点。

(2)描点．．:将选定的几个点分别按要求平移,得到它们的对应点,描出各点。

(3)连点．．:根据原图的形状顺次连接各对应点,得到的图形就是原图形平移后的图形。

6.运用平移知识解决面积、周长问题。