当前位置：文档之家 › 第四章静电场中的导体

第四章静电场中的导体

  • 格式：pptx
  • 大小：1.32 MB
  • 文档页数：81

下载文档原格式

  / 81

合集下载

大学物理复习第四章知识点总结

大学物理复习第四章知识点总结

大学物理复习第四章知识点总结大学物理复习第四章知识点总结一．静电场：1.真空中的静电场库仑定律→电场强度→电场线→电通量→真空中的高斯定理qq⑴库仑定律公式：Fk122err适用范围：真空中静止的两个点电荷F⑵电场强度定义式：Eqo⑶电场线：是引入描述电场强度分布的曲线。

曲线上任一点的切线方向表示该点的场强方向，曲线疏密表示场强的大小。

静电场电场线性质:电场线起于正电荷或无穷远，止于负电荷或无穷远，不闭合，在没有电荷的地方不中断，任意两条电场线不相交。

⑷电通量：通过任一闭合曲面S的电通量为eSdS方向为外法线方向1EdS⑸真空中的高斯定理：eSoEdSqi1int只能适用于高度对称性的问题：球对称、轴对称、面对称应用举例：球对称：0均匀带电的球面EQ4r20(rR)(rR)均匀带电的球体Qr40R3EQ240r(rR)(rR)轴对称：无限长均匀带电线E2or0(rR)无限长均匀带电圆柱面E(rR)20r面对称：无限大均匀带电平面EE⑹安培环路定理：dl0l2o★重点：电场强度、电势的计算电场强度的计算方法：①点电荷场强公式+场强叠加原理②高斯定理电势的计算方法：①电势的定义式②点电荷电势公式+电势叠加原理电势的定义式：UAAPEdl(UP0)B电势差的定义式：UABUAUBA电势能：WpqoPP0EdlEdl(WP00)2.有导体存在时的静电场导体静电平衡条件→导体静电平衡时电荷分布→空腔导体静电平衡时电荷分布⑴导体静电平衡条件:Ⅰ.导体内部处处场强为零,即为等势体。

Ⅱ.导体表面紧邻处的电场强度垂直于导体表面，即导体表面是等势面⑵导体静电平衡时电荷分布:在导体的表面⑶空腔导体静电平衡时电荷分布:Ⅰ.空腔无电荷时的分布：只分布在导体外表面上。

Ⅱ.空腔有电荷时的分布(空腔本身不带电，内部放一个带电量为q的点电荷)：静电平衡时，空腔内表面带-q电荷，空腔外表面带+q。

3.有电介质存在时的静电场⑴电场中放入相对介电常量为r电介质，电介质中的场强为：E⑵有电介质存在时的高斯定理：SDdSq0,intE0r各项同性的均匀介质D0rE⑶电容器内充满相对介电常量为r的电介质后，电容为CrC0★重点：静电场的能量计算①电容：②孤立导体的电容C4R电容器的电容公式C0QQUUU举例：平行板电容器C圆柱形电容器C4oR1R2os球形电容器CR2R1d2oLR2ln()R1Q211QUC(U)2③电容器储能公式We2C22④静电场的能量公式WewedVE2dVVV12二.静磁场：1.真空中的静磁场磁感应强度→磁感应线→磁通量→磁场的高斯定理⑴磁感应强度：大小BF方向：小磁针的N极指向的方向qvsin⑵磁感应线：是引入描述磁感应强度分布的曲线。

4静电场中的导体

4静电场中的导体

3) 推论：处于静电平衡的导体是等势体 导体表面是等势面 导 体 是 等 势 体
en
E dl
E
+
+ + +
E dl 0
导体内部电势相等
dl
+
+
et
U AB E dl 0
AB
A
B
注意 当电势不同的导体相互接触或用另一导体（例如导 线）连接时，导体间将出现电势差，引起电荷宏观 的定向运动，使电荷重新分布而改变原有的电势差， 直至各个导体之间的电势相等、建立起新的静电平 衡状态为止。
各个分区的电场分布（电场方向以向右为正）：
1 2 3 4 在Ⅰ区：E 2 0 2 0 2 0 2 0 1 Q 方向向左 0 2 0 S
Eint 0
◆ 导体表面紧邻处的场强必定和导体表面垂直。
E S 表面
证明(1)：如果导体内部有一点场强不为零，该点的 自由电子就要在电场力作用下作定向运动，这就不 是静电平衡了。 证明(2)：若导体表面紧邻处的场强不垂直于导体表 面，则场强将有沿表面的切向分量 Et，使自由电子 沿表面运动，整个导体仍无法维持静电平衡。
const .
E dS
S
q
i
i
0
E dl 0
L
3. 电荷守恒定律
讨论题：
1. 将一个带电+q、半径为 RB 的大导体球 B 移近一 个半径为 RA 而不带电的小导体球 A，试判断下列说 法是否正确。 +q B (1) B 球电势高于A球。 (2) 以无限远为电势零点，A球的电势 A 0 。 (3) 在距 B 球球心的距离为r ( r >> RB ) 处的一点P， q /(40。 r2) 该点处的场强等于 (4) 在 B 球表面附近任一点的场强等于 B / 0 ，

静电场中的导体和电解质

静电场中的导体和电解质

Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0

i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi

大学物理-静电场中的导体

大学物理-静电场中的导体

E内= 0 等势体
静电平衡时的导体
接地 ：取得与无限远相同的电势 通常取为零）。 （通常取为零）。
6
半径为R的金属球与地相连接 的金属球与地相连接， 例1. 半径为 的金属球与地相连接，在与球心 相距d=2R处有一点电荷 处有一点电荷q(>0)，问球上的 相距 处有一点电荷 ， 感应电荷 q'=? q'？q =
q3
q2 q1
B
R1 R2
A
R3
22
解: （1）当球体和球壳为一般带电体时 ） 用高斯定理可求得场强分布为
r −R E3 = (q1 + 3 Q) ( R2 ≤ r ≤ R3 ) 2 4πε0r R3 − R 1
3 3 2 3 2
4πε0 R q1 E2 = 2 4πε0r
E1 =
q1
3 1
r
(r ≤ R1 )
E = σ / εo
1 3.面电荷密度正比于表面曲率 σ ∝ R 面电荷密度正比于表面曲率
31
例4-2 （3）如果外壳接地，情况如何？ ）如果外壳接地，情况如何？ （4）如果内球接地，情况又如何？ ）如果内球接地，情况又如何？ （3）如果外壳接地 ） 则： 外壳电势= 外壳电势= 无穷远处电势 =0 外壳带电量= 外壳带电量=Q’
S
ε0 V
S 是任意的。 是任意的。 令S→ 0，则必有ρ 内 = 0。 。
8
必为零。 2.导体壳： 外可不为零，但σ内 和 E内必为零。 导体壳： 可不为零， 导体壳 σ
σ内 = 0
E内 = 0
S内
σ外
理由： 理由： 在导体中包围空腔选取 高斯面S 高斯面 ， 则：
S
r r ∫ E导内 ⋅ d s = 0

大学物理电磁学公式总结

大学物理电磁学公式总结

大学物理电磁学公式总结➢ 第一章（静止电荷的电场）1. 电荷的基本性质：两种电荷，量子性，电荷守恒，相对论不变性。

2. 库仑定律：两个静止的点电荷之间的作用力F =kq 1q 2r 2e r =q 1q 24πε0r 2e r3. 电力叠加原理：F=ΣF i4. 电场强度：E=Fq, q 0为静止电荷5. 场强叠加原理：E=ΣE i用叠加法求电荷系的静电场：E =∑q i4πε0r i 2e ri i (离散型) E=∫dq4πε0r 2e r q(连续型)6. 电通量：Φe=∫E •dS s7. 高斯定律：∮E •dS s=1ε0Σq int 8. 典型静电场：1) 均匀带电球面：E=0 （球面内）E=q 4πε0r 2e r （球面外）2) 均匀带电球体：E=q 4πε0R3r =ρ3ε0r （球体内）E=q4πε0r 2e r （球体外） 3) 均匀带电无限长直线：E=λ2πε0r ，方向垂直于带电直线4) 均匀带电无限大平面：E=σ2ε0，方向垂直于带电平面9. 电偶极子在电场中受到的力矩：M=p×E➢ 第三章（电势）1. 静电场是保守场：∮E •dr L=0 2. 电势差：φ1 –φ2=∫E •dr (p2)(p1)电势：φp =∫E •dr (p0)(p) （P0是电势零点） 电势叠加原理：φ=Σφi 3. 点电荷的电势：φ=q 4πε0r电荷连续分布的带电体的电势：φ=∫dq4πε0r4. 电场强度E 与电势φ的关系的微分形式：E=-gradφ=-▽φ=-(∂φ∂xi +∂φ∂yj +∂φ∂zk )电场线处处与等势面垂直，并指向电势降低的方向；电场线密处等势面间距小。

5. 电荷在外电场中的电势能：W=q φ移动电荷时电场力做的功：A 12=q(φ1 –φ2)=W 1-W 2电偶极子在外电场中的电势能：W=-p •E➢ 第四章（静电场中的导体）1. 导体的静电平衡条件：E int =0，表面外紧邻处Es ⊥表面 或导体是个等势体。

静电场中的导体

静电场中的导体
静电场中的 导体
一、导体的静电平衡条件
+
++++ + + + +
感应电荷
静电平衡条件
导体 内部 的场
E0
E E0 E'
E'
静电平衡时
E E' E0
E E0 E' 0
外场
E0
•静电平衡条件： 导 感应场 E '
体内部场强为0。
导体内部的场 E
二、处于静电平衡的导体的性质
1.静电平衡时导体为等势体，导体表面 为等势面。
R2 R3
(1)球壳B内、外表面上的电量及球A和球壳B的电势
(2)将球壳B接地然后断开，再把金属球A接地，求金 属球A和球壳B内、外表面上各带有的电量以及球A 和球壳B的电势
• 例:有一块大金属平板,面 积为S,带有总电量Q,在 其近旁平等放置第二块 大金属板,此板原来不带 电.求静电平衡时,金属板 上的电荷 分布及其空间
如尖端放电
三、静电空腔内表面无电荷,全部电 荷分布于外表面。
证明：在导体内作高斯面
S
E
dS
q
0
导体内 E 0, q 0
面内电荷是否会等量异号？
如在内表面存在等量异号 电荷，则腔内有电力线， 电势沿电力线降落，所以 导体不是等势体，与静电 平衡条件矛盾。
所以内表面无电荷，所有电荷分布于外表 面。
• 不管外电场如何变化，由于导体表面电 荷的重新分布，总要使内部场强为 0。
• 空腔导体具有静电屏蔽作用。例如：高 压带电作业人员穿的导电纤维编织的工 作服。
2.腔内有电荷
空腔原带有电荷 Q ，将 q 电荷放入空腔内。 结论：

大学物理电磁学典型习题

大学物理电磁学典型习题

部分习题解答第一章 静止电荷的电场1、10 解：（一定要有必要的文字说明）在圆环上与角度θ相应的点的附近取一长度dl ，其上电量 dq =λdl =0λsinθdl ，该电荷在O 点产生的场强的大小为==204RdqdE πε2004sin R dl πεθλθπελsin 400R =θd dE 的方向与θ有关，图中与电荷 dq 对O 点的径矢方向相反。

其沿两坐标轴方向的分量分别为 θθθπελθd RdE dE x cos sin 4cos 00-=-=θθπελθd RdE dE y 200sin 4sin -=-=整个圆环上电荷在圆心处产生的场强的两个分量分别为==⎰x x dE E R004πελ-⎰=πθθθ200cos sin d==⎰Y y dE E R004πελ-⎰-=πελθθ200024sin Rd 所以圆心处场强为 E = E y j = R004ελ-j 1、11 解：先将带电系统看成一个完整的均匀带电圆环计算场强，然后扣除空隙处电荷产生的场强；空隙的宽度与圆半径相比很小，可以把空隙处的电荷看成点电荷。

空隙宽度m d 2102-⨯=，圆半径m r 5.0=，塑料杆长m d r l 12.32=-=π 杆上线电荷密度m C lq/1019-⨯==λ 一个均匀带电圆环，由于电荷分布关于圆心对称，环上对称的二电荷元在圆心处产生的场强互相抵消，因而整个圆环在圆心处的场强E 1= 0 空隙处点电荷设为q /，则q / =d λ，他在圆心处产生的场强m V rdr q E /72.0442020/2===πελπε 方向由空隙指向圆心。

空隙处的电荷实际上不存在，因此圆心处场强等于均匀带电圆环在该点产生的场强与空隙处电荷在该点产生的场强之差，故m V E E E /72.021-=-= 负号表示场强方向从圆心指向空隙。

1、12 解：设想半圆形线CAD 与半圆形线ABC 构成一个圆形如图，且圆上线电荷密度均为λ。

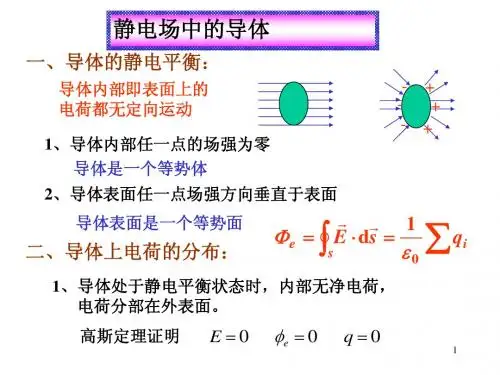
静电场中的导体

静电场中的导体

'
'
13
电偶极矩： 斜柱体的体积：
' ql Sl V Sl cos
电极化强度矢量的大小： p

' p cos pn
3、电介质的极化规律，极化率：
' V cos
p
极化强度矢量与该点的合场强有关，并与介质有关 对大多数各向同性电介质
2、电容器及其电容： 平板电容：
同轴柱形电容器 设 长 为 l
s c 0 d
C AB
qA U A UB
带电量为 q 外半径为 RB
8
内半径为 RA 则 q l
L
E 2 0 r B U AB E dl

A

RB

q c 2 0 U AB
同心球形电容器
1.0 102 m 处的电势
3、把点电荷移开球心，导体球壳的电势是否变化？
10 4 . 0 10 解：1、 V 9 109 40 R2 3.0 10 2
q
+q
-q
120v
2、定义
R1
+q
V1

R1
q 4 0 r
2
r1
dr


R2
q 4 0 r
0
s
E
0
2
尖端放电的实质 三、静电屛蔽：
+
+ + + + +
+ +
四、导体存在时静电场的计算： 例1、金属板面积为S，带电量为 Q。近旁平行放置第二块不 带电大金属板。 1、求电荷分布和电场分布；

静电场中的导体

静电场中的导体

静电场中的导体2.1 填空题2.1.1 一带正电小球移近不带电导体时，小球将受到（ ）力作用；一带负电小球移近不带电导体时，小球将受到（ ）力作用；一带正电小球靠近不带电的接地导体时，小球将受到（ ）力作用。

2.1.2 在一个带正电的大导体附近P 点放置一个点电荷q(电荷q 不是足够小)，实际测得它的受力为F ，如果q>0, 则F/q 与P 点场强E 0关系为（ ），如果q<0, 则F/q 与P 点场强关系为( )2.1.3 导体在静电场中达到静电平衡的条件是（ ）和（ ）。

2.1.4 导体处于静电平衡状态时，导体内部电荷体密度（ ），电荷只能分布在（ ）。

2.1.5 导体处于静电平衡状态时，导体是（ ）体，表面是（ ）面。

2.1.6 接地导体的电势等于（ ），地球与（ ）等电势。

2.1.7 一导体球壳，内外半径分别为R 1和R 2，带电q ，球壳内还有一点电荷q ，则导体球壳的电势是（ ）。

2.1.8 一点电荷q 放在一接地的无限大导电平面附近，则导电平面上的总电量为（ ）。

2.1.9 将一个点电荷+q 移近一个不带电的导体B 时，则导体B 的电势将（ ）。

2.1.10 一封闭导体壳C 内有一些分别带q 1、q 2…的带电体，导体壳C 外也有一些分别带Q 1、Q 2…的带电体，则q 1、q 2…的大小对导体壳C 外的电场强度（ ）影响，对C 外的电势（ ）影响；Q 1、Q 2…的大小对导体壳C 内的电场强度（ ）影响，对C 内的电势（ ）影响。

2.1.11 两个同心导体球壳A 、B ，若内球B 上带电q ，则电荷在其表面上的分布呈（ ）分布；当从外边把另一带电体移近这两个同心球时，则内球B 上的分布呈（ ）分布。

2.1.12 两导体球半径分别为r A 和r B ，A 球带电q ，B 球不带电，现用一细导线连接，则分布在两球上的电荷之比Q A ∶Q B （ ）。

2.1.13 在带等量异号电荷的二平行板间的均匀电场中，一个电子由静止自负极板释放，经t 时间抵达相隔d 的正极板，则两极板间的电场为（ ），电子撞击正极板的动能为（ ）。

电场中的导体和电介质

电场中的导体和电介质

二、电容器
1、电容器的定义
两个带有等值而异号电荷的导体 所组成的系统，叫做电容器。
+Q
-Q
2、电容器的电容
如图所示的两个导体放在真空中，它们所 带的电量为+Q、-Q，它们的电势分别为 V1、V2，定义电容器的电容为： 计算电容的一般步骤为： •设电容器的两极板带有等量异号电荷； •求出两极板之间的电场强度的分布； •计算两极板之间的电势差； •根据电容器电容的定义求得电容。
3-4 物质中的电场
在静电场中总是有导体或电介质存在的，而且静电场 的一些应用都要涉及静电场中导体和电介质的行为， 以及它们对静电场的影响。
一、静电场中的导体
1、静电感应及静电平衡
若把导体放在静电场中，导体中的自由电子将在电场力的 作用下作宏观定向运动，引起导体中电荷重新分布而呈现 出带电的现象，叫作静电感应。 开始时， E’< E0 ，金属内部的场强不零， 自由电子继续运动，使得E’增大。这个过 程一直延续到E’= E0即导体内部的场强为零 时为止。此时导体内没有电荷作定向运动， 导体处于静电平衡状态。




根据静电平衡条件，空腔 由静电平衡条件，腔内壁非均匀 分布的负电荷对外效应等效于： 导体内表面总的感应电荷为 -q， 非均匀分布；外表面，总的感 在与 q 同位置处置 q 。 应电荷为 q，非均匀分布。
9





R


q q q U U U U U 0 q 壳 地 内壁 外壁 q q O o d q外壁 0
C Q V
Q C＝ 4 0 R V

静电场中的导体

静电场中的导体
E2 4 0 r 2
R1 r R2
E3
1
4
0
Q q/ r2
U
R1
E.dr
R2 R1
E2.dr
R2 E3.dr 0
r R2
q/
4 0
1 R1
1 R2
1
4 0
Q q/ R2
0,
解得
q
R 1
Q
R
2
故外球壳外表面荷电 Q q/ Q R1 Q
R2
17
10
例8－１4 如图所示，一带正电Q的点电荷离半径为R的金属球壳 外的距离为d，求金属球壳上的感应电荷在球心O处的场强。
q/
R
r
E0 0 E/ d
Q
解 以球心为坐标原点，球心指向点电荷的方向为矢径方向，则
点电荷在球心处的场强
Q
E0 4 0 (R d )2 r0
又
E E/ E 0
内
0
q
总之，导体壳内部电场不受壳外电荷的影响，接地导体使 得外部电场不受壳内电荷的影响。这种现象称为静电屏蔽。
12
２、尖端放电
在带电尖端附近，电离的分子与周围分子碰撞，使周围的 分子处于激发态发光而产生电晕现象。
+ +
++ +++
+ +
+++
+
尖端效应在大多数情况下是有害的：如高压电线上的电晕， 故此，高压设备中的金属柄都做成光滑的球形。
△s面上σ均匀， E1=常矢 ，且垂直于导体表面，又E内＝０
e
E表
E s1 1
0
ds
s

电磁学第四章恒定电流和电路

电磁学第四章恒定电流和电路

dq en dS u dt
J enu
铜导线一般 n～1028m-3 ，u～0.15mm/sec 所以，电流密度大小为J～104 库/秒米2。
6
4. I 与 J 的关系：
通过导体中任意截面 S的电流 强度为：
I
导体中各点的 J 可以有不同的量值和方向，它是空
电流密度矢量的通量等于该面内 电荷量的减少率. 物理实质：电荷守恒定律. 3.恒定电流和恒定电场

S
要在导体中维持恒定电流，必须在导体内建立 dq 一个不随时间变化的恒定电场.这就要求激发 dt 0 电场的电荷分布不随时间变化，即
9
电流稳恒条件
J dS 0
S
上式表明，形成恒定电流时，在导体内从任一闭合 曲面流入的电荷量等于流出的电荷量. 恒定电场 激发电场的电荷分布不随时间变化，所建立 起的电场也不随时间变化，称为恒定电场. 讨论: ①稳恒的含义是指物理量不随时间改变. 稳恒条件可说成电荷分布不随时间变化，而并不意 味着电荷不能运动. 形成恒定电流的电荷处于宏观的定向运动状态之中.
电流线上每一点的切线方向就是 的方向，电流线的疏密表示它 J 的大小。 J 即| | 电流线的疏密度。
根据电荷守恒，在有电流分布的空间作一闭合 曲面，单位时间内穿入、穿出该曲面的电量等于 曲面内电量变化速率的负值。
8
2.电流连续性方程
dq J dS dt S
§4.4 电动势和全电路欧姆定律
4.4.1 非静电力
稳恒电流线必然是闭合的。然而仅有静电场不可能实现稳恒 电流。因为静电场的一个重要性质是
E dl 0
L
即电场力沿闭合回路移动电荷所做的功为0。若电场力将电 荷从一点移到另一点做正功，电势能减小，则从后一位置 回到原来位置电场力做负功，电势能增加。由于导体存在 电阻，电场移动电荷所做的功转化为电阻上消耗的焦耳热， 这就不可能使电荷再返回电势能较高的原来位置，即电流 线不可能是闭合的。结果引起电荷堆积，破坏稳恒条件。

恒定电场

恒定电场
第四章 恒定电场
什么是恒定电场？
处于静电场中的导体，其内部的电场强度为零。 如果将导体与电源的两极相连，则导体内部就会 有电流产生。而想要维持电流的存在，则导体内 部的电场强度就不为零。那么这个维持电流的电 场就是恒定电场。 电流的描述 电流强度 I 就是单位时间流过导线某一截面的电 荷量
dq I dt
的电位要满足拉普拉斯方程。
2 0
边界条件
E1t E2 t J 1n J 2 n
7
第四章 恒定电场
对于电位，则有
1 2 1 2 1 n 2 n
8
第四章 恒定电场
恒定电场与静电场的比拟 均匀导电媒质中的恒 均匀电介质中的静电 定电场（电源外部） 场（ 0 的区域）
J 0 微分形式 E 0 本构方程 J E
6
第四章 恒定电场
同静电场一样，由于 E 0 ，所以我们可以 引入一个标量函数电位 ，有 E 。 将其带入 J 0 ，我们同样可以得到恒定电场

第四章 恒定电场
电流密度 J 就是在垂直于电荷流动方向的截面上， 某点处单位面积内的电流总量，那么通过面元 dS 的电流为
dI J d S
I
流过任意截面 S 的电流强度为
S
J dS
2
第四章 恒定电场
图 4.1 电流与电流密度
(a) 体电流；(b) 面电流；(c) 线电流
基本方程
S J d S 0 l E dl 0 J 0 E 0
S D d S 0 l E dl 0 D 0 E 0

静电场(导体电介质能量)

静电场(导体电介质能量)

U r R1
U R1 R2
qB q A q A 1 q A q A q A qB qA ( )
4 0 r R2 R3
q A q A q A qB ( ) 4 0 R1 R2 R3 1
B
A
R1 R2
R3
U R2 R3
q A qB 4 0 R3
E 介质中的总场强(外电场＋束缚电荷电场)
r称为相对介电常数或相对电容率
P 0 e E, e r 1 e …称为电极化率,
四、束缚电荷与极化强度的关系 以无极电介质为例推导 如图，在电介质表面上取一面 元dS, 并在电介质中沿极化强 度方向取一图所示的斜柱体。
1 2
由电荷守恒:
1 2 0
(1)
由静电平衡条件: B内部E=0 即：E0+E1-E2 = 0
0
E2
1
2
E1
0 1 2 0 2 0 2 0 2 0
E0
0 1 2 0
解（1）（2）的联立，得
(2)
1
0
2
, 2
0
2
E
E in 0

0
3、孤立导体处于静电平衡时，导体表面上的电荷面 密度与曲率成正比。 导体表面曲率半径愈小处(即 曲率愈大处),电荷面密度愈大， 电场也愈大.
尖端放电
雷击尖端
§ 有导体存在时静电场的分析与计算
基本依据: (1)利用导体静电平衡条件 (2)利用电荷守恒定律 (3)利用高斯定理 (4)利用环路定理
= 0 r 称为电介质的介电常数
由电介质中的高斯定理容易证明：无限大均匀电 介质中(或两等势面间充满均匀电介质)的电场：

静电场中的导体习题

静电场中的导体习题

《静电场中的导体》习题一、判断题1在带正电的导体A附近，有一不接地的中性导体B，则A离B越近时，A 的电位越低。

[]2、接地导体，其表面必处处无电荷。

[]3、静电平衡时，电力线不能由导体一端的正电荷发出而终止于该导体另一端的负电荷。

[]4、静电感应达到平衡时，凡是接地导体必不带电。

[]5、由于静电感应，在导体表面的不同区域出现异号电荷，因而导体不再是等位体。

[]6、由于中性导体壳B对带电体A的屏蔽作用，带电体A的电场将对验电器C 无影响。

[]7、由于静电屏蔽作用，空腔导体内的带电体在腔外产生的场强为零。

[ ]8静电平衡时，导体表面是等位面，所以导体表面附近的场强大小处处相等。

[]二、选择题：1、在串联电容电路中，若电压逐渐升高，对耐压值相同的电容器来说，先击穿的将是[]A、电容值小的B、电容值大的C、同时击穿D无法确定2、在一个带正电荷，电量为Q的大导体附近P点放一个带电量也为Q的点电荷，若此时点电荷受到的斥力大小为F，则F/Q与未放置此点电荷时场强E相比（）A、大于B、相等C、小于3、在一带电为Q的导体壳A内有一接地的导体球B，A与B不接触，静电平衡时导体球B上所带电量q,则q为（）A、零；B、符号与Q相反，且（q<QC、符号与Q相同，且（q <Q4、两个同心得均匀带电球面，半径分别为R i和R2,且R2=2R I，内球面带正电荷q i，要使内球面的电位为正值，则外球面的电量q2必须满足[ ](1)内、外场强分布均匀⑶内外场强分布都不均匀10、如右图所示，将一个带正电的金属小球移近一个A 、q 2>-q iB 、q 2>-2q iC 、q 2=-2q iD 、q 2<-2q i5、 平行板电容器充电后与电源断开，然后使极板间距增大，则 []A C T UJ E JB 、C J UT E T C 、C J UT E 不变D C T UJE 不变6、 如图所示，三个无限大均匀带电平面，面电荷密度均为 c,相互平行放置,E 沿x 正方向为正，则P 点的E 为[]A3b f 3cr cr a A 、… B 、 C 、 D 、2 2电 2心 2昴_ | d .6 如图所示，已知 C i =6 卩 F ，C 2=3 卩 F ，R=6Q, R 2=3Q ，若IU de =18V,则a 、b 两点间的电压为[]y l L 3i-' A 、0 B -6V C 、6V D 12V脸 T c?7、 中性金属球壳A 内有一带电体B ，如图所示各个电场线图 匸中，哪一个图正确地表示出球壳内外的场强分布 []&如图 所示，导体空腔腔内有一电荷q 和测量仪器A,腔外有一电荷Q 和测量仪器B ,则测量 仪器测得的结果是[]A 、 只测到q 的场，B 只测到Q 的场 B 、 A 只测到q 的场，B 能测到q 和Q 的场C 、 A 能测到q 和Q 的场，B 只能测到Q 的场D A 能测到q 和Q 的场，B 也能测到q 和Q 的场9、在一金属壳的内部放一点电荷 (不在导体壳中心),则金属壳内外电场分布((2)内场强不均匀，外场强均匀 (4)内场强均匀，外场强不均匀绝缘的不带电的导体时，贝u （ ）（1）A 端电势高 （2）B 端电势高 （3）电势相等 （4）电势相等11、 有两个半径均为R ,分别带电+Q 和-Q 的金属球，球心相距为d , （d>R ），它 们的相互作用力大小为F i 。

第四章 静电场中的导体

第四章 静电场中的导体
外不变，E外不变，q外 Q q不变。
Qq
+q
2º若将腔内带电体与导体壳连接， 会出现什么情况？
腔内无电荷分布：E内=0 屏蔽外场
Q
q
3º若将导体壳接地， 又会出现什么情况？
+q
q外 0 导体壳外：E外=0
屏蔽内场
12
静电屏蔽 在静电平衡的条件下：
当腔内有带电体时，将壳接地，
腔内带电体的电场对壳外无影响
E3
4 0
Q1 Q2
2 0S
如第二块金属板右边接地
① 左边导体板总电量不变，但右边导体板 总电量变化
27
(1 2 )S Q1
(1)
② 导体内任意一点场强=0
1 2 3 4 0
(3)
20 20 20 20
1 2 3 4 0 20 20 20 20
(4)
2 3 1 4 0
+q
屏蔽内场 在外电场中， 导体壳内和腔内无电场， 腔内物体不会受外界影响
EE==00
屏蔽外场
Q+q
13
五、有导体存在时静电场的分析与计算
例1 一半径为 R1的带电球体A，总电量q1 ，在它 外面有一个同心的带电球壳B，其内外半径分别为 R1 和R2 ，总电量Q。 试求:
（1）此系统的电场
分布及电势分布。
σ等于零）。
37
在球状导体的情况下： 接地点的电势等于无穷远处的电势等 于零，但与地相连的表面一般有电荷。
注意：公式 E / o 中E是所有表面
电荷产生的总场强大小。 σ是 紧靠场点处那个带电表面的面
电荷密度。而 E / 2o中E是
无限大平板情况下一个表面的 电荷产生的场强大小。

大学物理静电场中的导体

大学物理静电场中的导体
E仅由S 处电荷产生而与其它电荷无关吗？为什么？
★ 注意：
导体表面外侧附近的场强 E是空间所有电荷共同激发的！
例：
q
P
E内0
EP4q0R20
q
P
E内0
Q
E
P
0
由
q 共同激发 。
Q
.
27
电导块势场
.
28
尖端放电 原理
尖端场强特别强，足以使周围空气分子电离而使 空气被击穿，导致“尖端放电” ，避雷针原理在此。
+ SA++
+
+
B--B +
+ +
+ +
32
b、空腔内有带电体
EdS0 S1
qi 0
Qq
电荷分布在表面上
思考：内表面上有电荷吗？
S E 2 d S0qi0
S2
q
q
S1
结论：
q内 q
腔体内表面所带的电量和腔内带电体所带的电量等量 异号，腔体外表面所带的电量. 由电荷守恒定律决定。33
三 静电屏蔽
ua ub E•dl
p 等势面 等势体
体体 是
a
a
Q
等
E内0 ua ub
b
导体表面
Q Q
u Pu QE •dlE co 90 s0 d l0
P
P
uP uQ
.
16
处于静电平衡状态的 导体的性质：
1、导体是等势体，导体表面是等势面。
2、导体外部附近空间的场强与导体表面正交。
3、导体内部处处没有未被抵消的净电荷，净电荷只 分布在导体的表面上。
1 R2 2 R1

第四章 导体

第四章 导体

4
23
1 2 3 4 Ep 0 2 0 2 0 2 0 2 0
+
1 2 3 4 0
(4)
1 2
3
4
Q Q 1 , 2 , 2S 2S Q Q 3 , 4 2S 2S
P
Q
1
2 3
3
由 (1)和（2）有， q3 Q－q2 Q＋q1 q1 E内 ( R1 r R2 ) 2 40 r q3 q1 Q E外 (r R3 ) 2 2 dl
A
29

R2
40 r q1 1 1 ( ) 40 R1 R2
S
21
解：(1)求电荷分布和场强 由电荷守恒定律: Q 1 2 (1) S 3 4 0 (2)
1
2
3
4
22
P
取圆柱形高斯面，根据高斯定律可得
2 3 0 (3)
将两块金属板看成四个无限大带电面，由 场强迭加原理，取向右方向为正方向，有
1
2
3
１）导体壳 屏蔽外电场。 ２）导体壳接地 屏蔽内电场。
应用：
1）屏蔽罩（设备不受干扰）
2）屏蔽线（微弱信号不受干扰）
三、有导体存在时静电场的分析与计算
分析方法: 静电平衡条件(E导内=0) 电荷守恒（ 导体不接地） 高斯定律 注意： 若导体接地： E内=0， 导= 地。 常见导体组: 板状，球状
1
第4章
静电场中的导体
本章研究把导体引进静电场中导 体与电场的相互作用规律，重点介绍 导体在静电平衡下的电荷、电场、电 势分布及求解方法。
2
第4章 静电场中的导体
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二、静电平衡(Electrostatic Equilibrium)
当外电场和导体上重新分布的电荷所产生的 电场对自由电荷的作用相互抵消，导体中宏观 的电荷运动停止，电荷又达到新的平衡分布， 这种状态称为静电平衡。
2
三、静电平衡条件
（1）导体内部任何一点的场强等于 0 。
（2）导体表面任何一点的场强都垂直表面 。
（1）此系统的电场
分布及电势分布。
（2）如果球体和球壳 q3
均为导体，再求电场 分布和电势分布
q2
R1
q1
R2
A
R3
B 13
解:
（1）当球体和球壳为一般带电体时（自己完成）
用高斯定理可求得场强分布为
E1
q1
4 0 R13
r
(r R1 )
E2
q1
4 0r 2
(R1 r R2 )
E3
1
4 0r 2
n
则有 E dS E4 r 2
qi q1 Q
S
i 1
n
qi
根据高斯定理 E dS i1
S
0
有
E4 4 r 2 (q1 Q) 0
E4
q1 Q
4 0r 2
(r R3)
18
电势分布 ( 0)
球体内 (r R1 )
感应电荷 q'=?
q'？= q
解： 利用金属球是等势体
R
球体上处处电位: U= 0
o
球心处： Uo= 0
即：q04dqoR
q 4o2R
0
q
o
dq 4oR
q 4o
2R
q R
q 2R
q
q 2
R q
9
四、静电屏蔽(Electrostatic Shielding)
空心导体如果腔内没有净电荷，在静电平 衡时，电荷都分布在外表面，内部无电场， 所以，如果把任一物体放入空心导体的空 腔内，该物体就不会受任何电场的干扰， 这就是静电屏蔽的原理。
例如：在均匀场放入一导体的情况
E
E
E内 0
表面出现感应电荷
电荷不动
电荷积累到一定程度 E E 达静电平衡
推论：
1º导体是等势体。 2º导体表面是等势面。
3
四、导体上电荷分布
1. 导体内无净电荷，电荷体密度 0
电荷只能分布在表面上。
①实心导体: ②空腔导体
体内无净电荷,即： 0
电荷分布在表面上。
以静电平衡为前提
10
讨论
1º腔内+q所处位置不同，对内外表
Q+q q S
+q
面电荷分布及电场分布的影响。动画
内改变 , E内改变, q内 q不变。
外不变，E外不变，q外 Q q不变。
Qq
+q
2º若将腔内带电体与导体壳连接， 会出现什么情况？
腔内无电荷分布：E内=0 屏蔽外场
Q
q
3º若将导体壳接地， 又会出现什么情况？
16
n
则有
E dS E 4 r 2
S
n
qi q1
i 1
qi
根据高斯定理
E dS i1
S
0
有
E2
4 r 2
q1
0
E2
q1
4 0r 2
(R1 r R2 )
球壳中
(R2 r R3 )
*因球壳是导体， 所以 E3 0
17
球壳外 (r R3 )
作与带电体同心、半径= r 的球面形高斯面
(q1
r 3 R23 R33 R23
Q)
(R2 r R3 )
E4
q1 Q
4 0r 2
(r R3 )
14
电势分布 ( 0)
球体内 (r R1 )
r
R1 r
E1dr
R2 R1
E2dr
R3 R2
E3dr
R3 E4dr
r
R2 r
E2dr
R3 R2
E3dr
R3 E4dr
(R1 r R2 )
则有：
dS
0
侧EdS
上E dS E S
E
o
1 o
qi
S o
E S
6
3 电荷面密度与导体表面曲率的关系
孤立导体：在给定电荷情况下电荷分布有如下定性规律
实验结论：面电荷密度正比于表面曲率
1 R
即：曲率
1 较大 R
（表面凸起处）
较大
曲率
1 R
较小
（表面较平坦处）
较小
曲率
1 为负 R
（表面凹进处）
更小
E
表面尖端处，E较大 表面平坦处，E较小 表面凹进处，E最弱
++ ++
+ +
+ +
+++++++++++
7
当曲率很大的尖端E很强
尖端放电
尖端放电
利用： 避雷针 除尘器 火花放电设备
危害： 损失电能 污染环境
8
例1. 半径为R的金属球与地相连接，在与球心
相距d=2R处有一点电荷q(>0)，问球上的
+q
qi 0
i
qi q q内 0
i
即：q内 q 得证
由电荷守恒： q外 Q q
5
2. 带电导体表面附近任一点的场强大小与该点 附近导体表面的电荷面密度成正比,即：
E /o
方向: 垂直该场点附近的导体表面
S 在导体表面上任取面积元 S，该处电
荷面密度 ,作底面积为S的高斯圆柱面，
轴线垂直S
导体 将实物按电特性划分： 半导体
非导体带电体
绝缘体
动画
① 所带电荷在带电体上不能自由移动
② 电荷体密度 0
导体带电体
E
① 所带电荷在带电体上可以自由移动
② 电荷体密度 0 ，电荷只能分布在表面
（ 静 电 平 衡 状 态 时）
1
一、静电感应(Electrostatic Induction)
当导体受到外电场作用时，不论导体原来 是否带电，导体中的运动电荷，在外电场力 的作用下，将相对于晶体点阵作宏观运动， 引起导体上电荷重新分布的现象，称为静电 感应现象。
腔内无电荷： 导体上无净电荷，电荷体密度 0
内表面无净电荷
电荷全分布在导体外表面
4
腔内有电荷q: 空腔导体带电Q
导体上无净电荷， 电荷体密度 0
空腔导体内表面带电总量 q内 q
空腔导体外表面带电总量 q外 q Q
证明：在导体壳内作一高斯面S
Q+q q S
由高斯定理：
vv
Ñ E dS 0
r
R3 r
E3dr
R3 E4dr
(R2 r R3 )
r r E4dr
(r R3 )
15
（2）如果球体和球 壳均为导体， 再求电场分布
和电势分布。 q3
球体内 (r R1 )
*因球体是导体，
所以: E1 0
q2
R1
q1
R2
A
R3
B
球体外、球壳内表面内 (R1 r R2 )
作与带电体同心、半径= r 的球面形高斯面
+q
q外 0 导体壳外：E外=0
屏蔽内场
11
静电屏蔽 在静电平衡的条件下：
当腔内有带电体时，将壳接地，
腔内带电体的电场对壳外无影响
+q
屏蔽内场 在外电场中， 导体壳内和腔内无电场， 腔内物体不会受外界影响
EE==00
屏蔽外场
Q+q
12
五、有导体存在时静电场的分析与计算
例1 一半径为 R1的带电球体A，总电量q1 ，在它 外面有一个同心的带电球壳B，其内外半径分别为 R1 和R2 ，总电量Q。 试求: