最新第七章静电场中的导体
- 格式:doc
- 大小:231.00 KB
- 文档页数:9
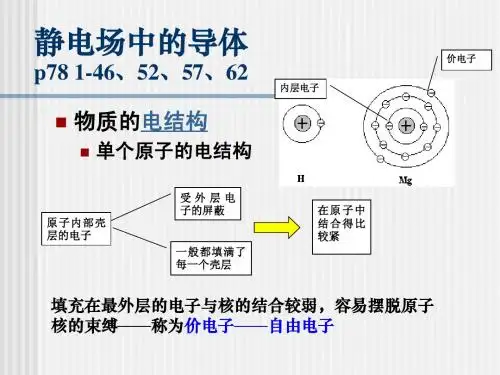





专业班级_____ ________学号________第七章静电场中的导体和电介质一、选择题:1,在带电体A旁有一不带电的导体壳B,C为导体壳空腔的一点,如下图所示。
则由静电屏蔽可知:[ B ](A)带电体A在C点产生的电场强度为零;(B)带电体A与导体壳B的外表面的感应电荷在C点所产生的合电场强度为零;(C)带电体A与导体壳B的表面的感应电荷在C点所产生的合电场强度为零;(D)导体壳B的、外表面的感应电荷在C点产生的合电场强度为零。
解答单一就带电体A来说,它在C点产生的电场强度是不为零的。
对于不带电的导体壳B,由于它在带电体A这次,所以有感应电荷且只分布在外表面上(因其部没有带电体)此感应电荷也是要在C点产生电场强度的。
由导体的静电屏蔽现象,导体壳空腔C点的合电场强度为零,故选(B)。
2,在一孤立导体球壳,如果在偏离球心处放一点电荷+q,则在球壳、外表面上将出现感应电荷,其分布情况为 [ B ](A)球壳表面分布均匀,外表面也均匀;(B)球壳表面分布不均匀,外表面均匀;(C)球壳表面分布均匀,外表面不均匀;(D)球壳的、外表面分布都不均匀。
解答 由于静电感应,球壳表面感应-q ,而外表面感应+q ,由于静电屏蔽,球壳部的点电荷+q 和表面的感应电荷不影响球壳外的电场,外表面的是球面,因此外表面的感应电荷均匀分布,如图11-7所示。
故选(B )。
3. 当一个带电导体达到静电平衡时:[ D ](A) 表面上电荷密度较大处电势较高 (B) 表面曲率较大处电势较高。
(C)导体部的电势比导体表面的电势高。
(D)导体任一点与其表面上任一点的电势差等于零。
4. 如图示为一均匀带电球体,总电量为+Q ,其外部同心地罩一、外半径分别为r 1、r 2的金属球壳、设无穷远处为电势零点,则在球壳半径为r 的P 点处的场强和电势为: [ D ](A )E=r Q U r Q 0204,4πεπε=(B )E=0,104r Q U πε= (C )E=0,rQ U 04πε=(D )E=0,204r Q U πε=5. 关于高斯定理,下列说法中哪一个是正确的? [ C ](A )高斯面不包围自由电荷,则面上各点电位移矢量D为零。

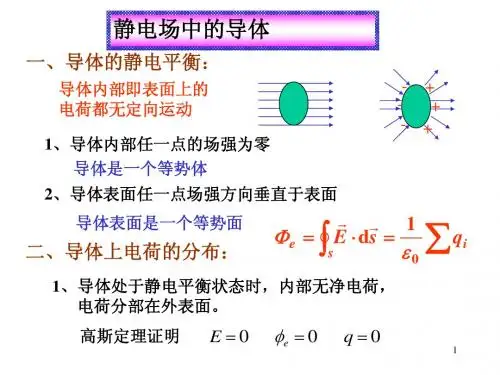

静电场中的导体2.1 填空题2.1.1 一带正电小球移近不带电导体时,小球将受到( )力作用;一带负电小球移近不带电导体时,小球将受到( )力作用;一带正电小球靠近不带电的接地导体时,小球将受到( )力作用。
2.1.2 在一个带正电的大导体附近P 点放置一个点电荷q(电荷q 不是足够小),实际测得它的受力为F ,如果q>0, 则F/q 与P 点场强E 0关系为( ),如果q<0, 则F/q 与P 点场强关系为( )2.1.3 导体在静电场中达到静电平衡的条件是( )和( )。
2.1.4 导体处于静电平衡状态时,导体内部电荷体密度( ),电荷只能分布在( )。
2.1.5 导体处于静电平衡状态时,导体是( )体,表面是( )面。
2.1.6 接地导体的电势等于( ),地球与( )等电势。
2.1.7 一导体球壳,内外半径分别为R 1和R 2,带电q ,球壳内还有一点电荷q ,则导体球壳的电势是( )。
2.1.8 一点电荷q 放在一接地的无限大导电平面附近,则导电平面上的总电量为( )。
2.1.9 将一个点电荷+q 移近一个不带电的导体B 时,则导体B 的电势将( )。
2.1.10 一封闭导体壳C 内有一些分别带q 1、q 2…的带电体,导体壳C 外也有一些分别带Q 1、Q 2…的带电体,则q 1、q 2…的大小对导体壳C 外的电场强度( )影响,对C 外的电势( )影响;Q 1、Q 2…的大小对导体壳C 内的电场强度( )影响,对C 内的电势( )影响。
2.1.11 两个同心导体球壳A 、B ,若内球B 上带电q ,则电荷在其表面上的分布呈( )分布;当从外边把另一带电体移近这两个同心球时,则内球B 上的分布呈( )分布。
2.1.12 两导体球半径分别为r A 和r B ,A 球带电q ,B 球不带电,现用一细导线连接,则分布在两球上的电荷之比Q A ∶Q B ( )。
2.1.13 在带等量异号电荷的二平行板间的均匀电场中,一个电子由静止自负极板释放,经t 时间抵达相隔d 的正极板,则两极板间的电场为( ),电子撞击正极板的动能为( )。


第7章 静电场中的导体和电介质 习题及答案1. 半径分别为R 和r 的两个导体球,相距甚远。
用细导线连接两球并使它带电,电荷面密度分别为1σ和2σ。
忽略两个导体球的静电相互作用和细导线上电荷对导体球上电荷分布的影响。
试证明:Rr =21σσ 。
证明:因为两球相距甚远,半径为R 的导体球在半径为r 的导体球上产生的电势忽略不计,半径为r 的导体球在半径为R 的导体球上产生的电势忽略不计,所以半径为R 的导体球的电势为R R V 0211π4επσ=14εσR= 半径为r 的导体球的电势为r r V 0222π4επσ=24εσr= 用细导线连接两球,有21V V =,所以Rr =21σσ 2. 证明:对于两个无限大的平行平面带电导体板来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同。
证明: 如图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ (1)取与平面垂直且底面分别在A 、B 内部的闭合圆柱面为高斯面,由高斯定理得S S d E S∆+==⋅⎰)(10320σσε 故 +2σ03=σ上式说明相向两面上电荷面密度大小相等、符号相反。
(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又 +2σ03=σ 故 1σ4σ=3. 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量。
解:如图所示,设金属球表面感应电荷为q ',金属球接地时电势0=V由电势叠加原理,球心电势为=O V R qdq R 3π4π4100εε+⎰03π4π400=+'=Rq R q εε 故 -='q 3q 4.半径为1R 的导体球,带有电量q ,球外有内外半径分别为2R 、3R 的同心导体球壳,球壳带有电量Q 。
第七章 静电场中的导体、电介质一、选择题:1. 已知厚度为d 的无限大带电导体平板,两表面上电荷均匀分布,电荷面密度均为σ,如图所示,则板外两侧的电场强度的大小为:[ ](A )E=02εσ (B )E=02εσ (C )E=0εσ (D )E=02dεσ2. 两个同心薄金属体,半径分别为R 1和R 2(R 2>R 1),若分别带上电量为q 1和q 2的电荷,则两者的电势分别为U 1和U 2(选无穷远处为电势零点),现用导线将两球壳相连接,则它们的电势为[ ](A )U 1 (B )U 2 (C )U 1+U 2 (D )21(U 1+U 2) 3.如图所示,一封闭的导体壳A 内有两个导体B 和C ,A 、C 不带电,B 带正电,则A 、B 、C 三导体的电势U A 、U B 、U C 的大小关系是(A )U A =U B =U C (B )U B > U A =U C(C )U B >U C>U A (D )U B >U A>U C4.一厚度为d 的“无限大”均匀带电导体板,电荷面密度为σ,则板的两侧离板的距离均为h 的两点a 、b 之间的电势差为: [ ](A )零 (B )02εσ (C )0εσh (D )02εσh5. 当一个带电导体达到静电平衡时: [ ](A) 表面上电荷密度转大处电势较高 (B) 表面曲率较大处电势。
(C)导体内部的电势比导体表面的电势高。
(D)导体内任一点与其表面上任一点的电势差等于零。
6. 如图示为一均匀带电球体,总电量为+Q ,其外部同心地罩一内、外半径分别为r 1、r 2的金属球壳、设无穷远处为电势零点,则在球壳内半径为r 的P 点处的场强和电势为: [ ](A )E=rQ U rQ 0204,4πεπε=(B )E=0,104r Q πε(C )E=0,rQ 04πε (D )E=0,204r Q πε7. 设有一个带正电的导体球壳,若球壳内充满电介质,球壳外是真空时,球壳外一点的场强大小和电势用E 1,U 1表示;若球壳内、外均为真空时,壳外一点的场强大小和电势用E 2、U 2表示,则两种情况下,壳外同一处的场强大小和电势大小的关系为: [ ](A )E 1=E 2, U 1=U 2 (B )E 1=E 2, U 1>U 2 (C )E 1>E 2, U 1>U 2 (D )E 1<E 2, U 1<U 28.一个未带电的空腔导体球壳,内半径为R ,在腔内离球心的距离为d 处(d<R ),固定一电量为+q 的点电荷,用导线把球壳接地后,再把地线撤去,选无穷远处为电势零点,则球心O 处的电势为 [ ](A )0 (B )04q dπε (C )-Rq 04πε (D))11(40Rd q-πε 9. 金属球A 与同心球壳B 组成电容器,球A 上带电荷q ,壳B 上带电荷Q ,测得球与壳间电势差为U AB ,可知该电容器的电容值为 [ ](A )q/U AB (B )Q/U AB (C )(q+Q)/U AB (D )(q+Q)/(2U AB ) 10. 如右图所示,有一接地的金属球,用一弹簧吊起,金属球原来不带电,若在它的下方放置一电量为q 的点电荷,则 [ ] (A) 只有当q>0时,金属球才下移。
(B) 只有当q<0时,金属球才下移。
(C) 无论q 是正是负金属球都下移。
(D) 无论q 是正是负金属球都不动。
11. 有一带正电荷的大导体,欲测其附近P 点处的场强,将一带电量为q 0(q 0>0)的点电荷放在p 点,如图所示,测得它所受的电场力为F ,若电量q 0不是足够小,则 [ ](A )F/q 0比P 点处场强的数值大。
(B )F/q 0比P 点处场强的数值小。
(C )F/q 0比P 点处场强的数值相等。
q。
q OA BQ Rd +q(D )F/q 0点处场强的数值关系无法确定。
12. A 、B 为两导体大平板,面积均为S ,平行放置,如图所示,A 板带电荷+Q 1,B 板带电荷+Q 2,如果使B 板接地,则AB 间电场强度的大小E 为 [ ](A )SQ 012ε (B )S Q Q 0212ε-(C )SQ 01ε (D )S Q Q 0212ε+13. 关于高斯定理,下列说法中哪一个是正确的?[ ](A )高斯面内不包围自由电荷,则面上各点电位移矢量D为零。
(B )高斯面上处处D为零,则面内必不存在自由电荷。
(C )高斯面的D通量仅与面内自由电荷有关。
(D )以上说法都不正确。
14.一导体外为真空,若测得导体表面附近电场强度的大小为 E ,则该区域附近导体表面的电荷面密度 σ 为[ ](A )ε0E/2 (B )ε0E (C )2ε0E (D )无法确定15. 孤立金属球,带有电量1.2×10-8C,当电场强度的大小为3×106V/m 时,空气将被击穿,若要空气不被击穿,则金属球的半径至少大于 [ ](A )3.6×10-2m (B )6.0×10-6m (C )3.6×10-5m (D )6.0×10-3m16. 将一空气平行板电容器接到电源上充电到一定电压后,断开电源,再将一块与板面积相同的金属板平行地插入两极板之间,则由于金属板的插入及其所放位置的不同,对电容器储能的影响为: [ ](A )储能减少,但与金属板位置无关。
(B )储能减少,且与金属板位置有关。
(C )储能增加,但与金属板位置无关。
(D )储能增加,且与金属板位置无关。
17. 两个完全相同的电容器C 1和C 2,串联后与电源连接,现将一各向同性均匀电介质板插入C 1中,则 [ ](A )电容器组总电容减小。
(B )C 1上的电量大于C 2上的电量。
(C )C 1上的电压高于C 2上的电压。
(D )电容器组贮存的总能量增大。
B1Q +218. 一空气平行板电容器,极板间距为d ,电容为C ,若在两板中间平行插入一块厚度为d/3的金属板,则其电容值变为 [ ](A )C (B )2C/3 (C )3C/2 (D )2C19. 面积为S 的空气平行板电容器,极板上分别带电量±q ,若不考虑边缘效应,则两极板间的相互作用力为: [ ](A )S 02q ε (B )S 022q ε (C )2022q S ε (D )202q Sε 20.三块互相平行的导体板,相互之间的距离d 1和d 2比板面积线度小得多,外面二板用导线连接,中间板上带电,设左右两面上电荷面密度分别为σ1和σ2,如图所示,则比值σ1/σ2为 [ ](A )d 1/d 2 (B )d 2/d 1 (C )1 (D )d 22/d 1221.C 1和C 2两个电容器,其上分别标明200pF (电容量)、500V(耐压值)和300pF 、900V ,把它们串连起来在两端加上1000V 电压,则 [ ](A )C 1被击穿,C 2不被击穿。
(B )C 2被击穿,C 1不被击穿。
(C )两者都被击穿。
(D )两者都不被击穿。
22. 一空气平行板电容器充电后与电源断开,然后在两极板间充满某种各向同性,均匀电介质,则电场强度的大小E 、电容C 、电压U 、电场能量W 四个量各自与充入介质前相比较,增大(↑)或减小(↓)的情形为: [ ](A )E ↑,C ↑,U ↑,W ↑ (B )E ↓,C ↑,U ↓,W ↓ (C )E ↓,C ↑,U ↑,W ↓ (D )E ↑,C ↓,U ↓,W ↑23.若某带电体的电荷分布的体密度ρ增大为原来的2倍,则其电场能量变为原来的[ ](A )2倍 (B )1/2倍 (C )4倍 (D )1/4倍24、用力 F 把电容器中的电介质拉出,在图(a )和图(b )的两种情况下, 电容器中储存的静电能量将 [ ] (A ) 都增加。
(B ) 都减少。
(C )(a )增加, (b )减少。
(D )(a )减少, (b )增加。
(a )充电后与电源连接 (b )充电后与电源断开3d25.一平行板电容器,充电后与电源保持联接,然后使两极板间充满相对介电常数为εr的各向同性均匀介质,这时两极板上的电荷,以及两极板间的电场强度、总的电场能量分别是原来的[ ](A)εr倍,1 倍和εr倍。
(B)1/εr倍,1 倍和εr倍。
(C)1 倍,1/εr倍和εr倍。
(D)εr倍,1 倍和1/εr倍。
二、填空题:1.两同心导体球壳,内球壳带电量+q,外球壳带电量-2q,静电平衡时,外球壳的电荷分布为:内表面带电量为;外表面带电量为。
2.将一负电荷从无穷远处移到一个不带电的导体附近,则导体内的电场强度,导体的电势。
(填增大、不变、减小)3.一任意形状的带电导体,其电荷面密度分布为σ(x、y、z),则在导体表面外附近任意点处的电场强度的大小E(x、y、z)= ,其方向。
4.一带电量为q半径为Ar的金属球A,与一原先不带电、内外半径分别为Br和Cr的金属球壳B同心放置如图.则图中P点的电场强度E= .如果用导线将A、B连接起来,则A球的电势U= .(设无穷远处电势为零)5.如图所示,把一块原来不带电的金属板B,移近一块已带有正电荷Q的金属板A,平行放置,设两板面积都是S,板间距离是d,忽略边缘效应,当B板不接地时,两板间电势差ABU= ;B板接地时'ABU= 。
6.如图示,A、B为靠得很近的两块平行的大金属平板,两板的面积均为S,板间的距离为d,今使A板带电量为q A,B板带电量为q B,且BAqq , 则A板的内侧带电量为;两板间电势差U AB= 。
S S+ + + + + + + + + + +7.如图所示,平行板电容器中充有各向同性均匀电介质,图中画出两组带有箭头的线分别表示电力线、电位移线,则其中(1)为,(2)为。
8.半径为R1和R2的两个同轴金属圆筒,其间充满着相对介电常数为εr的均匀介质,设两筒上单位长度带电量分别为+λ和-λ,则介质中的电位移矢量的大小D= ,电场强度的大小E= 。
9.一空气平行板电容器,两极板间距为d,极板上带电量分别为+q和-q,板间电势差为U,在忽略边缘效应的情况下,板间场强大小为,若在两板间平行地插入一厚度为t(t<d)的金属板,则板间电势差变为,此时电容值等于。
10.一平行板电容器,两板间充满各向同性均匀电介质,已知相对介电常数为εr,若极板上的自由电荷面密度为σ,则介质中电位移的大小D= ,电场强度的大小E= 。
11.在电容为C0的平行板空气电容器中,平行地插入一厚度为两极板距离一半的金属板,则电容器的电容C= 。