支路电流法例题

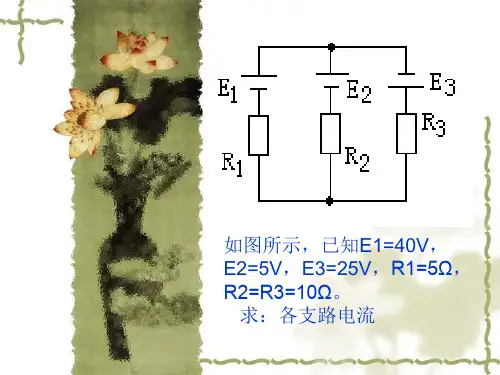
支路电流法说明：这是电工学课程直流电路章节中的一小节，故所用例题均为直流电路。

但支路电路法其实适用于任何电路的分析，是电路分析的基本方法。

一、引言（问题的引出）图1所示为一简单电路，它有三条支路，如果要求求出这三条支路的电流I 1、I 2、I 3，应该怎么办？(请学生思考并回答。

)图1 图2这个电路可通过欧姆定律及电阻串并联等效化简的方法方便地求解，如果电路变成图2，则又如何求解呢？是否可用同样方法求解呢？答案是否定的。

象这类仅仅用欧姆定律及电阻串并联等效化简的方法不能求解的电路称为复杂电路。

而支路电流法是求解复杂电路的最基本方法之一。

在支路电流法中，除了欧姆定律外，还要用到电路分析中的另一个重要定律：克希荷夫定律（或基尔霍夫定律）。

此时适当复习一下该定律。

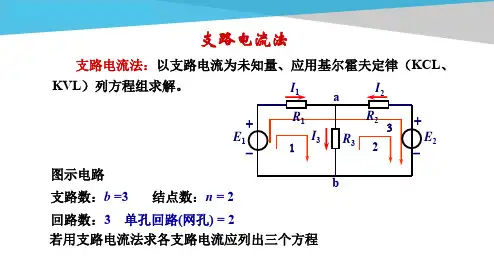
二、支路电流法支路电流法：以电路中的支路电流作为待求量，应用基尔霍夫电流定律（KCL ）和基尔霍夫电压定律（KVL ）分别对节点和回路列出所需要的方程电流。

支路电流求出后，其它电量就很容易得到。

下面用支路电流法计算图2电路的电流I 1、I 2、I 3。

1、 为了求解图2电路的3个支路电流I 1、I2、I 3，首先标出各个电流的正方 向，并明确应该列出3个互相独立的方程才能求解。

问题是这三个方程怎么列？2、 用克希荷夫定律列方程(1)先用 KCL 对节点列出方程（称节点电流方程）。

该电路有2个节点，设为A 、B 。

对节点A 有： I 1+I 2-I 3=0 (1) 对节点B 有： -I 1-I 2+I 3=0 (2)显然两式不独立，所以用KVL 可列出1个独立方程，现选（1）式。

一般地，对于有n 个节点的电路，只能列出n-1个独立电流方程。

RR 2 I 2U R2 U(2)然后用KVL 列出所需要的另二个方程（注意是独立方程），称回路电压方程。

选择二个回路，并设定其绕行方向如图所示。

（该电路共有三个回路） 对回路1应用KVL ，得：I 1R 1+I 3R 3-U S 1=0 (3) 对回路2应用KVL ，得：-I 2R 2-I 3R 3+U S 2=0 (4) 若再对回路3列方程：U S 1-I 1R 1+I 2R 2-U S 2=0 (5)很显然，该式是前二式的线性组合，不是独立方程，这样，用KVL 列出了2个相互独立的方程（3）和（4），当然也可以是（4）、（5）或（3）、（5）。

二、现以图1为例说明支路电流法的解题步骤任意设置各支路电流的参考方向（一条支路上只有一个电流）和网孔回路的绕行方向（如图1示）。

图11）、根据基尔霍夫电流定律（∑I=0）列独立的节点电流方程。

如果电路有2个节点，则只能列出1个独立的方程式。

如果电路有n个节点，则只能列出（n-1）个独立的方程式。

对于图中的节点B，其电流为I1+I2 =I3 （1）2）、根据基尔霍夫第二定律（∑u=0）列不足的回路电压方程。

上图1中共有三个未知电流，但只能列出1个独立的节点电流方程式，还要再列出两个独立的回路电压方程式，电路才能求解。

为保证回路的独立，每次所取的回路须含有一个新支路（即其他方程式中没有利用过的支路），则此回路电压方程式就是独立的，因此，我们一般选择网孔来列方程。

在列回路电压方程式时，可先标出各元件电阻两端电压的正、负极极性（如图2示）。

在用式∑u=0时，各段电压的正、负号是这样规定的：如果在绕行过程中从元件的正极点到负极点，此项电压便是正的；反之从元件的负极点绕到正极点，此项电压则是负的（简言之，“先遇正得正，先遇负得负”）。

例如图2中的两个网孔，沿图示绕行方向，根据∑u=0，得R1I1-I2R2+Us2-Us1=0 （2）I2R2+I3R3=Us2 （3）1、解联立方程组。

若已知E1，E2，R1，R2，R3，把这些已知数据代入（1）、（2）、（3）式中，得I1+I2-I3=0 (1)E1-E2=R1I1-I2R2 (2)E2=R2I2+R3I3 (3)I1= I2= I3=若为正值，电流实际方向与标明的参考方向相同；若为负值，电流的实际方向与标明的参考方向相反。

[例题1] 图所示电路中，已知电阻R1=5Ω,R2=10 Ω,R3=15Ω,E1=180v,E2=80v,求各支路电流解：(1) 设各支路电流参考方向、回路绕行方向如上图。

(2)利用KCL对节点A列写电流方程式得：I１+I２=I３(1)(3)利用KVL对回路列写电压方程式：(4)对回路ⅠE1= I１Ｒ１+I3Ｒ3 (2)(5)对回路ⅡＥ2＝Ｉ２Ｒ２＋Ｉ３Ｒ3 (3)(6)联立方程组，求出各支路电流I1+I2=I3 (1)Ｅ1=I１Ｒ１+I3Ｒ3 （2）Ｅ２＝Ｉ２Ｒ２＋Ｉ３Ｒ３（3）代入参数I1+I2-I3 =0180=5I１+15I380＝10I２＋15I３解联立方程可得：I1=12A,I2=-4A,I3=8A 求得结果中I1和I3是正值，说明电流的实际方向与参考方向是一致，I2为负值，说明电流的方向和实际方向是反向的。

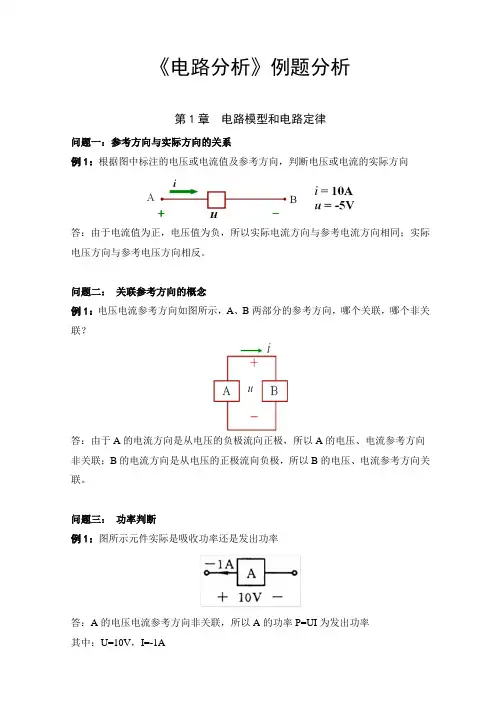
《电路分析》例题分析第1章电路模型和电路定律问题一：参考方向与实际方向的关系例1：根据图中标注的电压或电流值及参考方向，判断电压或电流的实际方向答：由于电流值为正，电压值为负，所以实际电流方向与参考电流方向相同；实际电压方向与参考电压方向相反。

问题二：关联参考方向的概念例1：电压电流参考方向如图所示，A、B两部分的参考方向，哪个关联，哪个非关联？答：由于A的电流方向是从电压的负极流向正极，所以A的电压、电流参考方向非关联；B的电流方向是从电压的正极流向负极，所以B的电压、电流参考方向关联。

问题三：功率判断例1：图所示元件实际是吸收功率还是发出功率答：A的电压电流参考方向非关联，所以A的功率P=UI为发出功率其中：U=10V，I=-1A所以：A发出功率P=UI=-10W，即，实际吸收10W。

例2：计算图示电路各元件的功率答：电压源的电压电流为关联参考方向，则功率P5V=5*2=10W，吸收功率电流源电压电流为非关联参考方向，则功率P2A=5*2=10W，发出功率满足：吸收功率=发出功率问题四：受控源的类型例1：说明下列每个受控源的类型及控制量答：a：电压控制电流源（VCCS），控制量为20Ω电阻两端电压Ub：电流控制电流源（CCCS），控制量为20Ω电阻上的电流Ic：电流控制电压源（CCVS），控制量为10Ω电阻上的电流Id：电压控制电压源（VCVS），控制量为20Ω电阻两端电压U1问题五：基尔霍夫电流定律例1：求R4和R5上的电流答：先假设R4和R5上的电流方向，对右侧R1、R2和R3构成的回路利用KCL，求解出R4上的电流，再对R4左侧的结点利用KCL，求解R5上的电流，求解过程略。

例2：求图示电路中，I a=, I b=, I c=。

答：先标注三个10Ω电阻上的电流参考方向，再用欧姆定律分别求出三个电阻上电流的大小，最后利用三个结点的电流方程求出：I a=1.5A, I b=0, I c=-1.5A。

第二章 直流电路的分析与计算一、填空题1．所谓支路电流法就是以____为未知量，依据____列出方程式，然后解联立方程得到____的数值。

2．用支路电流法解复杂直流电路时，应先列出____个独立节点电流方程，然后再列出_____个回路电压方程〔假设电路有n 条支路，m 各节点，且n>m 〕。

3．根据支路电流法解得的电流为正值时，说明电流的参考方向与实际方向____；电流为负值时，说明电流的参考方向与实际方向____。

4.某支路用支路电流法求解的数值方程组如下：则该电路的节点数为____,网孔数为___。

10201002020502321321=-+=--=++I I I I I I I5.应用基尔霍夫定律计算出某支路电流是正值，表明该支路电流的_______方向与_______方向相同；支路电流是负值，表明_______。

6.基尔霍夫第一定律又称做_______定律，其数学表达式为_______。

7.基尔霍夫第二定律又称做_______定律，其数学表达式为_______。

8.电压源与电源的等效变换只对_______等效，对_______则不等效。

9.理想电压源的内阻r=_______，理想电流源的内阻r=_______，它们之间_______等效变换。

10.电压源等效变换为电流源时，I S =_______，内阻r 数值_______，由串联改为_______。

11.二端网络中有_______，叫做有源二端网络，二端网络中没有_______，叫做无源二端网络。

12.用戴维宁定理计算有源二端网络的等效电源只对_______等效，对_______不等效。

13.叠加原理只适用于_______电路，只能用来计算_______和_______，不能计算_______。

14.叠加原理的内容是_______。

15.有两个电阻R 1.R 2，已知R 1=2R 2，把它们并联起来的总电阻为4Ω，则R 1=_______，R 2=_______16．一有源二端网络，测得起开路电压为6V ，短路电流为3A ，则等效电压源为U s =___V, R 0=____Ω。

支路电流法解题例题支路电流法是一种用于求解电路中各支路电流的电路分析方法。

它的核心思想是将电路分解成若干个支路，然后根据支路之间的关系和电路的特性，利用电流流向法或电压降落法求解各支路电流。

下面以一个例题来介绍支路电流法的应用。

假设有一个电路，其中包括一个电源、一个电阻和一个电容，具体情况如下:电源电压:V = 12V电阻值:R = 10Ω电容值:C = 1μF求电路中各支路的电流。

首先，我们将电路分解成两个支路，即电源正极和电阻支路，以及电源负极和电容支路。

然后，根据电流流向法，我们将电流从电源正极流入，从电阻支路流出，再流回电源负极。

在电源正极和电阻支路交叉口，根据左手定则，电流方向从电阻支路指向电源正极。

因此，电阻支路上的电流为 i1 = V / R = 12V / 10Ω = 1.2A。

在电源负极和电容支路交叉口，由于电容支路中电流需要守恒，因此电流方向从电容支路指向电源负极。

因此，电容支路上的电流为i2 = (V - Us) / C = (12V - 120mV) / 1μF = 11.85A(其中，Us 为电源电压降落在电容上的电压)。

最终，我们可以使用支路电流法求解电路中各支路电流。

首先，计算电源正极和电阻支路交叉口的电流为 i1 = V / R = 12V / 10Ω = 1.2A。

然后，计算电源负极和电容支路交叉口的电流为 i2 = (V - Us) / C = (12V - 120mV) / 1μF = 11.85A。

最后，我们可以使用电流流向法，将两个支路上的电流相加，得到整个电路中的电流为i = i1 + i2 = 1.2A + 11.85A = 13.05A。

综上所述，支路电流法是一种用于求解电路中各支路电流的有效的方法。

它适用于各种类型的电路，可以快速、准确地求解电路中各支路电流。

支路电流法说明：这是电工学课程直流电路章节中的一小节，故所用例题均为直流电路。

但支路电路法其实适用于任何电路的分析，是电路分析的基本方法。

一、引言（问题的引出）图1所示为一简单电路，它有三条支路，如果要求求出这三条支路的电流I 1、I 2、I 3，应该怎么办？(请学生思考并回答。

)图1 图2这个电路可通过欧姆定律及电阻串并联等效化简的方法方便地求解，如果电路变成图2，则又如何求解呢？是否可用同样方法求解呢？答案是否定的。

象这类仅仅用欧姆定律及电阻串并联等效化简的方法不能求解的电路称为复杂电路。

而支路电流法是求解复杂电路的最基本方法之一。

在支路电流法中，除了欧姆定律外，还要用到电路分析中的另一个重要定律：克希荷夫定律（或基尔霍夫定律）。

此时适当复习一下该定律。

二、支路电流法支路电流法：以电路中的支路电流作为待求量，应用基尔霍夫电流定律（KCL ）和基尔霍夫电压定律（KVL ）分别对节点和回路列出所需要的方程电流。

支路电流求出后，其它电量就很容易得到。

下面用支路电流法计算图2电路的电流I 1、I 2、I 3。

1、 为了求解图2电路的3个支路电流I 1、I2、I 3，首先标出各个电流的正方 向，并明确应该列出3个互相独立的方程才能求解。

问题是这三个方程怎么列？2、 用克希荷夫定律列方程(1)先用 KCL 对节点列出方程（称节点电流方程）。

该电路有2个节点，设为A 、B 。

对节点A 有： I 1+I 2-I 3=0 (1) 对节点B 有： -I 1-I 2+I 3=0 (2)显然两式不独立，所以用KVL 可列出1个独立方程，现选（1）式。

一般地，对于有n 个节点的电路，只能列出n-1个独立电流方程。

RR 2 I 2U R2 U(2)然后用KVL 列出所需要的另二个方程（注意是独立方程），称回路电压方程。

选择二个回路，并设定其绕行方向如图所示。

（该电路共有三个回路） 对回路1应用KVL ，得：I 1R 1+I 3R 3-U S 1=0 (3) 对回路2应用KVL ，得：-I 2R 2-I 3R 3+U S 2=0 (4) 若再对回路3列方程：U S 1-I 1R 1+I 2R 2-U S 2=0 (5)很显然，该式是前二式的线性组合，不是独立方程，这样，用KVL 列出了2个相互独立的方程（3）和（4），当然也可以是（4）、（5）或（3）、（5）。