当前位置：文档之家 › 轴测投影的基本概念汇总

轴测投影的基本概念汇总

  • 格式：ppt
  • 大小：436.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

工程制图：第九章 轴测投影图简介

工程制图：第九章 轴测投影图简介
轴测轴之间的夹角称为轴间角
2、 轴测轴、轴间角和轴向变形系数
X、Y、Z轴的轴向变形系数：
p O1 A1 , q O1B1 , r O1C1
OA
OB
OC
②空间坐标轴上的
单位长度投影到轴 测投影面上，得到 相应的轴测轴上的 单位长度，它们与 原来坐标轴上的单 位长度的比值称为
轴向变形系数
Z1
C1 A1 O1 B1
13
P.130
二、正等轴测图
3、 平行于坐标面的圆的正等测画法
1) 圆的正等测（椭圆）的画法
② 近似画法（四心法）
Z
①在正投影图上作圆的外切正方形
②画轴测轴，根据圆直径作外切正方形的 正等测—菱形。其对角线即椭圆的长、短 轴位置，顶点为大圆弧的圆心
14
③ 如图连接，交点为小圆弧的圆心 ④ 分别作大、小圆弧，即完成椭圆
1'(2')
3' 6' (4') 9' (7') 8' (10')
5'
10 7 8
2 (4)
45°
5
Ⅱ1 Ⅳ1
Ⅶ1 Ⅹ1 Ⅷ1
Ⅴ1
Ⅰ1 Ⅲ1 Ⅵ1
Ⅸ1
9 6 1(3)
P.133
例9-8 已知圆柱被截切后的两面投影，画出其正等测图
1'(2')
3' 6' (4') 9' (7') 8' (10') 5'
• 在长方体上截去左侧一角
09
二、正等轴测图
例2：
Z 18
2、 平面立体的正等测画法
Z
Z
10

第五章轴测投影详解

第五章轴测投影详解
按投射线与投影面是否垂直分为：正轴测图 斜轴测图 按轴向伸缩系数的不同情况分为：等测 二测 三测 常用的轴测图为：正等测和斜二测
5.2 正等测
P
Z1
正轴测投影图
O1 X1
Y1 X
Z
S O
Y
正轴测投影图的形成
5.2.1 轴间角和轴向伸缩系数
投影线方向
投影线与轴测投影面垂直
轴向伸缩系数
p1=q1=r1=0.82
特 简化轴向伸缩系数
p=q=r=1
Z1
性
轴间角
120°O1 120°
X1
120°
Y1
L 0.82L
边长为L的正 方形的轴测图
按简化轴向伸缩系数绘制
按实际轴向伸缩系数绘制
正等测画图步骤:
(1) 在视图上建立坐标系 (2) 画出正等测轴测轴 (3) 按坐标关系画出物体的轴测图
5.2.2 平面立体正等测画法
第五章 轴测投影 5.1 轴测投影的基本概念 5.2 正等测 5.3 斜二测
5.1 轴测投影的基本概念
5.1.1 轴测投影的形成
正投影图
P
Z S
斜轴测投影图 Z1
S0 O
X
Y
O1 X1
Y1
投影面
Z1
O1
X1
Y1
Z
O
X
Y
将物体和确定其空间位置的直角坐标系，
沿不平行于任一坐标面的方向，用平行投影法
将其投射在单一投影面上所得的具有立体感的 图形叫做轴测图。
轴测轴
2. 轴向伸缩系数 物体上平行于坐标轴的线段在轴测图上的
长度与实际长度之比叫做轴向伸缩系数。
投影面
C1 Z1
ZC

机械制图中的轴测投影名词解释

机械制图中的轴测投影名词解释

机械制图中的轴测投影名词解释引言在机械制图中，轴测投影是一种表示三维物体的方法。

通过使用透视原理，将三维物体投射到一个平面上，并利用透视的原理在二维平面上重新构建物体的形状和尺寸。

本文将解释常用的轴测投影的名词和概念。

一、等轴测投影(Isometric Projection)等轴测投影是一种最为常见的轴测投影方法。

在等轴测投影中，物体的三个坐标轴都以等角度倾斜，并以相同的比例缩放，从而保持物体的形状和比例。

等轴测投影具有简单、直观、易于理解的特点，广泛应用于机械工程、建筑设计等领域。

二、斜二测投影(Oblique Projection)斜二测投影是一种较为简单的轴测投影方法。

在斜二测投影中，物体的一个主轴与投影平面垂直，而另外两个轴则以一定的角度倾斜。

斜二测投影相对于等轴测投影而言更能突出物体的特殊形态，如斜面、切口等。

三、正视图(Front View)正视图是指物体在投影平面上的正视图形。

一般情况下，我们习惯将物体的正视图作为平面图的正视(projection)。

正视图通常以平行投影的形式展示，即通过平行于投影平面的光线将物体投影到平面上。

正视图主要用于表示物体的外形和尺寸。

四、侧视图(Side View)侧视图是指物体在投影平面上的侧视图形。

与正视图类似，侧视图也以平行投影的形式展示。

通过侧视图，我们可以更好地了解物体的高度和厚度，并很容易观察到物体的不同侧面的特征。

五、俯视图(Top View)俯视图是指物体在投影平面上的俯视图形。

俯视图与正视图和侧视图不同的是，它是通过垂直于投影平面的光线将物体投射到平面上得到的。

俯视图可以完整显示物体的上表面，以及物体上的额外细节。

六、等轴测图(Orthographic Projection)等轴测图是通过将物体在三个正交投影面上的投影叠加而得到的图形。

等轴测图能够同时显示物体的三个视图，即正视图、侧视图和俯视图。

通过等轴测图，我们可以更全面地了解物体的各个面的特征，并准确地测量物体的各个尺寸。

轴测投影

轴测投影

3.作圆柱切口的轴测图，在椭圆上自1、2、3、4、5、6各点向上引垂线， 并截取相应高度即可作出；再根据圆柱的高度作圆柱的上顶圆；
1’(4’)
2’(5’)
3’(6’) 1 X
Z
Y 2 3
O
5 4 6
O 4 5 6 45°
45°
O
2
1
3
步骤： 1.画出轴测轴（为了看清切口，最好画成仰视的 轴测图）； 2.用八点法作出下底圆的斜二测椭圆；
在工程中，轴测投影图一般作为工程辅助图样。
返回
2、轴间角和轴向伸缩系数
轴测轴——三个坐标轴X1、Y1、Z1的轴测投影X、Y、Z。 轴间角——轴测轴之间的夹角，∠XOY、∠YOZ、∠ZOX 。 轴倾角——轴测轴X、Y与水平线间的夹角。
Z 轴向伸缩系数——轴测轴上的 C 单位长度与对应坐标轴上的单 位长度之比。 O X轴轴向伸缩系数: p=OA/O1A1 X A Y轴轴向伸缩系数: q=OB/O1B1 Z轴轴向伸缩系数：r=OC/O1C1 推论: 与坐标轴平行的棱线，其轴测投影平 行于对应的轴测轴，其轴向伸缩系数 等于对应坐标轴的轴向伸缩系数。 P
高校建筑学与城市规划专业教材《画法几何与阴影透视》课件编制：北京建筑工程学院 中国建筑工业出版社出版
5
Z′
X′ O′ Y Z Y
O X
O
返回
倒圆角正等轴测图的画法
Z
返回
返回
综合法
Z′ Z
X′
O′ O
X
Y
返回
Z′
Z
X′O′ O X YY′Z′ZX′
O′ O X Y
Y′ 返回
Z′ Z
X′
O′ O
X
Y

轴测投影的基本知识

轴测投影的基本知识

Page 11
1.线性尺寸 轴测图线性尺寸，应标注在各自所在的坐标面内，尺 寸线应与被注长度平行，尺寸界线应平行于相应的轴测轴， 尺寸数字的方向应平行于尺寸线，如出现字头向下倾斜时， 应将尺寸线断开，在断开处以水平方向注写尺寸数字。轴 测图的尺寸起止符号宜用小圆点。轴测图线性尺寸的标注 如图5-2所示。
（1）正等测图。三个轴向伸缩系数都相等的轴测 图，称为正等测图，简称正等侧。
(2）正二测图。只有两个轴向伸缩系数相等的轴测 图，称为正二测图，简称正二侧。
(3）正三测图。三个轴向伸缩系数都不相等的轴测 图，称为正三测图，简称正三侧。
单击此处编轴辑母测版标投题样影式
轴测投影的基本知识
2.斜轴测图 当投影方向倾斜于轴测投影面时得到的投影图， 称为斜轴测图。斜轴测图可分为正面斜轴测图和水平 斜轴测图。
轴测投影的基本知识
Page 3
单击此处编轴辑母测版标投题样影式
轴测投影的基本知识
Page 4
1.2 轴测图的基本参数 结合图5-1对轴测图的基本参数进行解释。 （1）轴测轴。 直角坐标轴的轴测投影轴，简称轴测轴，用O 1X 1、O 1Y 1、O 1Z 1表示。 （2）轴间角。 在轴测投影面P上，三个轴测投影轴之间的夹角称为 轴间角，用∠X 1O 1Z 1 ∠Y 1O 1Z 1、∠X 1O 1Y 1表示。
单击此处编轴辑母测版标投题样影式
轴测投影的基本知识
Page 12
单击此处编轴辑母测版标投题样影式
轴测投影的基本知识
Page 13
2.圆径尺寸 轴测图中的圆径尺寸应标注在圆所在的坐标面内； 尺寸线与尺寸界线应分别平行于各自的轴测轴。圆弧 半径和小圆直径尺寸也可引出标注，但尺寸数字应注 写在平行于轴测轴的引出线上。轴测图圆径尺寸的标 注如图5-3所示。

7-1 轴测投影的基本知识

7-1 轴测投影的基本知识

X1
Y1
木材科学与工程
19
第 七章轴测投影
3）凡是平行于V面的圆或曲线，常 用正面斜二测，其轴测投影反映实形，画 法较为方便。因此，凡具有正平圆或曲线 的立体采用正面斜二测图为宜。
木材科学与工程
20
第 七章轴测投影
木材科学与工程
21
第 七章轴测投影
2．轴测轴方向的变更 在确定了轴测图的类型后，只要保持轴间
第 七章轴测投影
第一节
轴测投影的基本知识
三面投影图可以比较全面地表示空间物体 的大小。但是这种图不能反映出立体的空间形 象，立体感较差，尤其是对初学者来说不容易 看懂。为弥补此缺陷，采用轴测投影绘出物体 的投影图，叫做轴测投影图。
木材科学与工程
1
第 七章轴测投影
测投影图立体感比较强，能同时反映几个 面的形状，但是它的缺点是不能直接反映物体 各表面的真实形状和大小，因而度量性较差， 同时作图较正投影复杂，所以多数情况下只能 作为一种辅助图样，用来帮助人们读懂正投影 图。
角不变，可以根据要求来变更轴测轴的方向。
也就是说，根据物体的形状选择一适当的投射
方向，使需要表达的部分最为明显。投射方向
的选择，相当于观察者选择从哪个方向去观察
物体。
木材科学与工程
22
第 七章轴测投影
木材科学与工程
23
第 七章轴测投影
木材科学与工程
24
第 七章轴测投影
作形体的轴测投影时，应根据形体的形状 特点，利用如直线的平行性等几何特性。辅助 直线、次投影、应用形体分析法、甚至近似法 等来简化作图。 一、平面立体
表面全是平面的立体，称为平面立体或多 面体 。 作平面立体的轴测投影，归结为作出其棱 线的轴测投影。当棱线平行坐标轴时，则直线 的长度可利用轴测轴的变形系数来量度。

第四章 轴测投影

第四章 轴测投影

O
b a Y
9
【例3】已知六棱柱的正投影图，完成其正等测图。
Z
Z1
1:1
h
30°
30°
X1
Y1 Z1
X
O
c
b a Y
X1
Y1
10
【例4】已知台阶的正投影图，完成其正等测图。
Z1
Z1
X1
Y1
X1
Y1
由XOY定位,立高度作图
由YOZ定位,拉长度作图
11
【例5】已知台阶的正投影图，完成其正等测图。
Z1
Z1
1:1
O1
30°
30°
X1
Y1
30
【例3】已知形体的三面投影图，作出它的正等测图。
Z'
Z1
X'
O'
O1 X1 Y1
X O
O1
Y
O2
31
【例4】已知形体的投影图，作出它的正等测图。
示意图
32
§4－4
二、圆的斜二测图
圆的轴测投影
Z1
在立方体的斜二测投影中，
正面保持不变，侧面和顶面的 正方形变成平行四边形，圆变
圆的轴测投影
在立方体的正轴测图中，其正方形都变成相等的菱形， 在其上面的圆也都变成相等的椭圆。在菱形里作内切椭圆， 最好用“四心圆弧法”。
Z1 Z1
X1
Y1
X1
Y1
俯视
仰视
27
§4－4
a b d
30° 1:1
圆的轴测投影
作图步骤：
1.画出正方形的中心线、对角线 2.在切点处作菱形各边线的垂线，得交
Z1 1:1 Y1 45°

第五章,轴测投影图

第五章,轴测投影图
截断
例2-2
画轴测轴 画 沿轴测量画动平面 各顶点沿Y方向画20 画动平面(终止位置) 画 检查、描深
*
例3 画出给定形体的正等轴测图
画空间轴 画轴测轴 画长方体 画五棱柱 检查、描深
例4 画出圆锥的正等轴测图
确定坐标轴 画轴测轴 画圆锥底面（侧平圆） 画锥顶 画转向线 判别可见性、描深
例5 根据已知的两面投影，画出正等轴测图
三、斜二轴测图画法
例13：已知两视图，画斜二轴测图。
第五章 轴测投影图
[例14] 作出如图所示带孔圆锥台的斜二轴测图。
z′
z〞
x′
o′
o〞
a″ y〞
L
Z1
X1
O1
L2
A
O1 A
Y1
圆弧公切线
[例15] 作出如图所示物体的斜二轴测图。
z′
z〞
x′
o′
L1
L
o〞 y〞圆弧公切线
Z1
X1 L1/2 L/2
2 平行于H面的圆为椭圆，长 轴对O1X1轴偏转7°， 长轴≈1.06d, 短轴≈0.33d。
3 平行于W面的圆与平行于H 面的圆的椭圆形状相同，长 轴对O1Z1轴偏转7°。
由于两个椭圆的作图相当繁，所以当物体这 两个方向上有圆时，一般不用斜二轴测图，而采 用正等轴测图。 斜二轴测图的最大优点：
物体上凡平行于V面的平面都反映实形。
x′
x1
2
z′
Z1
圆弧公切线
A
o′ o4
A1 41
o
31
11
3
X1
21
Y1
圆
弧
y
公 切
线
[例12] 作出如图所示支架的正等轴测。

7.1轴测投影的基本知识

7.1轴测投影的基本知识

轴测投影轴测投影的基本知识了解轴测图的形成；掌握正等测和斜二测的轴向变形系数和轴间角。

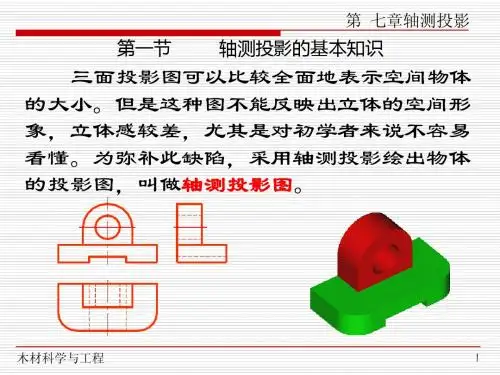
目的和要求S 0轴测投影的基本知识多面正投影图与轴测图的比较PZ 1X 1O 1Y 1ZOXY 正投影图S轴测投影的基本知识多面正投影 轴测投影度量性好，直观性差。

度量性不好，直观性较好。

轴测投影的基本知识一 概述1.轴测投影的形成YXZOP Z 1Y 1X 1O 1A 1C 1B 1C BAAa 1uuuk j iS轴测投影面 轴测投影轴测投影轴轴间角轴向变形系数p=i/u、 q=j/u、 r=k/u轴测投影的基本知识轴测：就是沿轴的方向量测的意思。

轴测投影坐标是由轴间角和轴向变形系数确定的。

所以轴测投影最基本的问题就是如何确定轴间角和轴向变形系数。

轴测投影的基本知识轴测投影采用的是平行投影法,所以:（1）物体上相互平行的线段，它们在轴测图中也相互平行且长度间的比例不变。

（2）平行于坐标轴的线段，其投影亦与相应轴测轴平行，其长度可按轴向变形系数求出。

轴测投影的基本知识PO 1X 1Y 1Z 1OZXYS正轴测投影图的形成正等轴测图正等轴测图 p = q = r 正二轴测图 p = r ≠ q 正三轴测图 p ≠ q ≠ r轴测投影的基本知识PZ1 X1O1Y1ZOX YS斜轴测投影图的形成斜二轴测图斜等轴测图 p = q = r斜二轴测图 p = r ≠ q斜三轴测图 p ≠ q ≠ r轴测投影的基本知识正等轴测投影图p=q=r=0.82， ∠X1O1Y1=∠Y1O1Z 1 = ∠X1O 1Z1 =120°轴测投影的基本知识斜二轴测投影图由图可知，斜二测图轴向变形系数和轴间角没有关联，均可任意选择，为了作图简便常取p=r=1,q=0.5，轴间角取α1 =45°。

课 程 小 结1. 轴测投影的基本概念；2. 正等测投影的轴间角和轴向变形系数；3. 斜二测投影的轴间角和轴向变形系数。

第6章轴测投影图

第6章轴测投影图
●B
Z1′
坐
标
O′
法
X1
Y1
Z
X
Y
返回
坐 标 法
返回
⑵ 切割法 例2：已知三视图，画轴测图。
切 割 法
返回
步骤一
返回
步骤二
返回
步骤三
返回
完成
返回
⑶ 叠加法 例3：已知三视图，画轴正等测图。
z′
o′
叠o 加 法
y
x′
x
Z
X
Y
返回
叠 加 法
返回
O′
X′
X Y
叠
加
Z′
法
O
X
Z
Y
返回
圆柱正等轴测图的画法
O′
O
X
Y
Z′
X
O
Y
Z
返回
圆柱正等轴测图的画法
Z′
O′ Y
X′ Y
X O
Z O
返回
例：画圆台的正等轴测图
⑵ 圆角的正等轴测图的画法
例：
简便画法：
★截取 O1D1=O1G1=A1E1=A1F1 =圆角半径
★作 O2D1⊥O1A1 ， O2G1⊥O1C1 O3 E1⊥O1A1 ， O3F1⊥A1B1
⑵ 作图步骤： •确定物体的坐标轴； •绘制正等测的轴测轴； •运用平行投影的特性作出物体上的点、线、面； •整理图线。加深加粗物体上可见的图线。
返回
⒈ 平面体的正等轴侧图画法
⑴ 坐标法 例1：画三棱锥的正等轴测图
s
Z Z s
S Z1 ●
X a b a
X
s
b
c OOcOca
Y
b

第3章 轴测投影

第3章 轴测投影

(a）正轴测投影图
(b）斜轴测投影图
图3-2 轴测投影图的形成
梁艳波 制作 舟山航海学校
建筑识图与构造
第3章 轴测投影
在轴测投影图中，空间坐标轴OX、OY、OZ在轴测投 影面P上投影为O1X1、O1Y1、O1Z1。O1X1、O1Y1、 O1Z1称为轴测投影轴，简称轴测轴；
轴测轴之间的夹角∠X1O1Y1、∠Y1O1Z1、∠Z1O1X1称 为轴间角；
第3章 轴测投影
舟山航海学校
建筑识图与构造
第3章 轴测投影
知识要点及学习程度要求
轴测投影的基本概念（理解） 轴测投影的种类和特点（了解） 正等测图的画法（掌握） 斜轴测图的画法（了解） 圆的轴测图的画法（掌握）
梁艳波 制作 舟山航海学校
建筑识图与构造
第3章 轴测投影
(a）正投影图
(b）轴测投影图
【例3-5】组合体的正等测图的画法（叠加法）如图3-8。
梁艳波 制作 舟山航海学校
建筑识图与构造
第3章 轴测投影
图3-8用叠加法作出组合体的轴测图 梁艳波 制作 舟山航海学校
建筑识图与构造
第3章 轴测投影
【例3-6】四坡顶的房屋模型的正等测画法，如图3-9。
梁艳波 制作 舟山航海学校
建筑识图与构造
要画曲面立体的轴测图必须先掌握平面上圆的轴测投影图的画法。根据正 投影图的原理可知，当圆所在的平面平行于投影面时，其投影仍为圆，而 当圆所在的平面倾斜于投影面时，它的投影为椭圆。在轴测投影中，除了 斜二测投影中有一个面不发生变形外，一般情况下的圆的轴测投影是椭圆。 图3-14为一个正方体表面三个内切圆的轴测图。
向右画，也可以选择向左画。
梁艳波 制作 舟山航海学校

轴测投影的基础知识

轴测投影的基础知识

轴测投影的基础知识
（2）斜轴测投影的形成，采用斜投影的方法向轴测投影面进行 投影，称为斜轴测投影。由这种方法画出来的图称为斜轴测投影图， 简称斜轴测图，如图6-1（b）所示。
图6-1轴测投影的形成 （a）正轴测投影（b）斜轴测投影
轴测投影的基础知识
2. 轴测轴、轴间角和轴向伸缩系数
（1）轴测轴。直角坐标轴OX、OY、OZ在轴测投影面上 的投影O1X1、O1Y1、O1Z1，称为轴测投影轴，简称轴测轴。
（2）轴间角。轴测轴之间的夹角∠X1O1Y1、∠Y1O1Z1、 ∠X1O1Z1称为轴间角。
（3）轴向伸缩系数。在空间三坐标轴上，分别取长度OA、 OB、OC，它们的轴测投影长度为O1A1、O1B1、O1C1，令
则p、q、r分别称为OX、OY、OZ轴的轴向伸缩系数。
轴测投影的基础知识
3. 轴测投影的分类
轴测投影的基础知识
1. 轴测投影的形成
轴测投影采用单面投影图，是平行投影之一， 它是把形体按平行投影法投射至单一投影面上所得 到的投影图，可分为以下两类：
（1）正轴测投影的形成，使其三个坐标轴方 向都倾斜于一个投影面P（轴测投影面），然后用 正投影的方法向该投影面投影，称为正轴测投影。 由这种方法画出来的图称为正轴测投影图，简称正 轴测图，如图6-1（a）所示。
轴测投影按轴测向变形系数分为以下三种： （1）正（或斜）等测，p=q=r。 （2）正（或斜）二测，p=r≠q。 （3）正（或斜）三测，p≠q≠r。 在道路工程中常采用正等测、正二测、斜二测三 种轴测图。这里仅介绍正等测、斜二测。
轴测投影的基础知识
4. 轴测投影的特点
物体上相互平
物体上平行于坐标
行线段的轴测投影 仍相互平行。

第五章 轴测投影

第五章 轴测投影

z1
x o y
o1 y1
x1
利用四心法
利用四心法作椭圆
（三）回转体正等测图的画法
z x’ z1 y’ y o1 o1 x1
z1
圆台的两视图
y1
圆台的两视图
判断可见性，
完成轴测图。
参见教材P118
切口圆柱正等轴测图的画法
Байду номын сангаас
完成圆角正等测图作图
第三节 斜二等轴测图
斜 —— 采用平行斜投影方法 二测 —— 三轴测轴的轴向伸缩系数中有两个 相等即 P=r ≠q
z’
z1
x’
o1
y1 x1
x
y
作立板，并判断可见性
（一） 平行于投影面的圆的正等测图的画法 立方体各面的正方形在轴测图中成了菱形。如果作 与正方形内切的圆，则该圆的正等测图为椭圆。
从立方体的轴测图可看出，三个不同位置的椭圆的方向是不 相同的。一般采用近似的四心圆弧法绘制正等测图中的椭圆。
（二）椭圆的画法：四心圆弧法
第二节 正等轴测图
使直角坐标系的三坐标轴OX、OY和OZ对轴测投影面的
倾角相等，并用正投影法将物体向轴测投影面投射，所得到
的图形称为正等轴测图，简称正等测。 正 —— 采用正投影方法 等 —— 三轴测轴的轴向伸缩系数 相同，即P=q =r
正等测图的两个参数 1.轴间角 由于直角坐标系的三坐标轴对轴测投影面的倾角相 等，根据理论分析三轴测轴的夹角均为120°
S
z1
x’ x
a` a s b`
o c`
c
C o1
y1
o
A x1
B
b
y
s`
z
三棱锥的正等测图：

建筑工程制图轴测投影

建筑工程制图轴测投影

【例 4】已知组合体旳正投影图，画出其正等测图。
O'
X' Y''
O''
Z'
Z''
Y
X
O
作图（切割法）：
（3）在长方体上切割掉一种较小旳长方体，形成一种 L 形形体
旳正等测图;
【例 】已知组合体旳正投影图，画出其正等测图。
O'
X' Y''
O''
Z'
Z''
Y
X
O
作图（切割法） ：
（4）在 L 形形体旳右侧较高部分切掉一种三棱柱，然后再在左
2. 八点法作圆旳轴测投影
z'
x’
o’ y’
A
7
D
Ep
Dp
7p
8
6
5p
Ap
x
o
1
5
Op
Cp
2
4
XP 1p
3p YP
B
3 y
C
作图：
Bp
（4）以平行四边形旳任一边长之半如Ap7p为斜边，作一等腰直
角三角形△Ap7pEp；
2. 八点法作圆旳轴测投影
z'
x’
o’ y’
A
7
D
Ep
8
6
7p
Dp 6p
5p
x 1
第二节 正轴测投影
一、正等轴测投影
1. 正等测旳轴间角与伸缩系数
正等测投影旳条件是投射方向与轴测投影面垂直，三个坐 标轴OX、OY、OZ 与轴测投影面倾斜而且倾角相等。
轴间角与 伸缩系数

第5章 轴测投影(OK)

第5章 轴测投影(OK)

水平斜轴测图，常用于绘制一个区域建筑群的总平面图，如下图所示。
【例5-5】已知建筑平面图如图5-8a所示，并已知建筑物的形状和高 度，试画出水平斜轴测图。
解：如图5-8b所示，取轴测投影轴X1 与水平线成30°，Y1轴与水平线成 60°，Z1位于铅垂位置，用铅垂方向表达建筑物的高度，画出建筑物的水平斜 轴测投影。 以水平斜轴测图来表达建筑物，既有平面图的优点，又具有直观性。图5-9a 所示的建筑群总平面图，其水平斜轴测投影如图5-9d所示。
第5章 轴测投影
图（a）为形体的三面正投影图，图（b）为同一形体的轴测投影图。
1.三面正投影图能够准确地表达出形体的形状，且作图简便，但直观性差，需要 受过专门训练者才能看懂； 2.轴测投影图的立体感较强，但度量性差，作图也较繁琐。
5.1 轴测投影的基本知识

一、轴测投影图的形成
轴测投影属于平行投影的一种 它是将形体连同确定其空间位置 的直角坐标系，用平行投影法，沿 S方向投射到选定的一个投影面P 上，所得到的投影称为轴测投影。 用这种方法画出的图，称为轴测投
线的交点。
（c）图是平面图形的正等测。其中圆弧D1B1是以O2为圆心，R2为半径画 出；圆弧B1C1是以O3为圆心，R3为半径画出。D1、B1、C1等各切点，均利 用已知的r来确定。

二、圆柱体的正轴测图 【例5-6】已知圆柱的V、H投影（见图5-11a）作出圆柱的正等轴测图。
解 1）确定参考坐标系：选顶圆的圆心为坐标原点，XOY坐标面 与上顶圆重合。 2）画出顶圆的轴测投影——椭圆，将椭圆沿Z轴向下平移H，即 得底圆的轴测投影，如图5-11 b所示。 3）作两椭圆的公切线；擦去不可见的部分，加深后即完成作图 ，如图5-11c所示。

轴测图基本知识

轴测图基本知识

轴测图基本知识:
一、基本概念
1．将物体及所在的直角坐标系沿不平行于任一坐标面方向，用平行投影法投射在投影面上获得的立体图的图形。

2．轴测投影面：获得轴测投影的平面
3．轴测轴：将互相垂直的直角坐标轴投射在轴测投影面上的投影。

4．轴间角：轴测轴之间的夹角。

5．轴向伸缩系数:
轴测投影长/实际长=轴向伸缩系数
X方向为p，y方向为q，z方向为r
P平方+q平方+r平方=1
二、性质
1．空间线段平行则轴测投影平行
2．平行坐标轴的线段投影长=实长乘以该轴的轴向伸缩系数
三、分类
1.正轴测图：投射线与轴测投影面垂直
包括：正等轴测图p=q=r=0.82 轴间角120°简化系数为1
正二轴测图p =r q=0.47 一个轴间角97°10‘，另两个轴间角131°25‘
简化系数为p=r=1，q=0.5
正三轴测图p，q，r不相等
2.斜轴测：投射线与轴测投影面倾斜
斜等轴测图p=q=r
斜二轴测图p =r 一个轴间角90°，另两个轴间角135°
简化系数为p=r=1，q=0.5
坐标面与轴测投影面平行，与坐标面平行的形状，轴测图反映实形。

斜三轴测图p，q，r不相等。

第六章 轴测投影

第六章 轴测投影

例2．画出图示建筑形体的水平斜二测。
作图：1、在建筑形体上选定直角坐标系。
2、画出轴测轴，根据正投影图，画出其水平投 影的水平斜二测，图（a）。
3、过平面图形各角点，向上作O1Z1轴平行线，截取各高 度，画出各顶面的水平斜二测，图（b）。
4、擦去多余作图线，描深，即完成建筑形体水平斜二测， 图（c）。
4、作出每一对等直径圆的公切线；图（c） 5、擦去多余作图线，描深，即完成形体的正面 斜二测。图（d）
二、水平斜轴测投影
水平斜二测的轴间角和轴向变形系数：坐标面XOY平 行于水平面，轴间角∠X1O1Y1=90°,轴向变形系数p=q=1， Z1轴向的变形系数可取任意值。选O1X1轴与水平线成30° 或60°。为简化作图，有时选轴向变形系数r=1。
3.斜三轴测图（正三测图）：三个轴测伸缩系数都不相等 （p ≠ q ≠ r）
第二节 正轴测图
一、正等测投影
当投射方向S垂直于轴测投影面P时，形体上三个坐标轴的轴向 变形系数相等，即三个坐标轴与P面倾角相等。此时在P面 上所得到的投影称为正等轴测投影，简称正等测。
根据计算，正等测的轴向变形系数p=q=r=0.82，轴间角 ∠X1O1Z1=∠X1O1Y1=∠Y1O1Z1=120°。画图时，规定把 O1Z1轴画成铅垂位置，因而O1X1轴、O1Y1轴与水平线均成 30°角，故可直接用30°三角板作图。
二、轴测轴方向的变更
在确定了轴测图的类型后，只要保持轴间 角不变，可以根据要求来变更轴测轴的方向。 也就是说，根据物体的形状选择一适当的投射 方向，使需要表达的部分最为明显。
第三节 斜轴测图
当投射方向S倾斜于轴测投影面P时，在P面上所 得到的投影称为斜轴测投影。
如果p=r，即坐标面XOZ平行于P面，得到的是正 面斜轴测；如果p=q，即坐标面XOY平行于P面， 得到的是水平斜轴测。

轴测投影的基本知识

轴测投影的基本知识

第五章轴测图如图5－1（a）所示的多面正投影图能完整、准确地反映物体的形状和大小，且度量性好，作图简便，但缺点是直观性差，只有具备一定读图能力的人才能看懂，有时工程上还需采用如图5－1（b）所示的立体感较强的图。

这种能同时反映物体长、宽、高三个方向形状，富有立体感的图，称为轴测投影图。

本章主要介绍轴测投影图的基本知识和画法。

图5－ 1 三视图与轴测图第一节轴测投影的基本知识一、轴测投影的形成如图5－2所示，将物体连同其参考直角坐标系，沿不平行于任一坐标面的方向，用平行投影法在单一投影面P上所得的具有立体感的图形，称为轴测投影图，简称轴测图。

图5－ 2 轴测图的形成在轴测图中，我们把这个单一投影面P称为轴测投影面，直角坐标系中的坐标轴OX、OY、OZ在轴测投影面上的投影O1X1、O1Y1、O1Z1称为轴测轴；而把每两根轴测轴之间的夹角，称为轴间角；三条直角坐标轴上的单位长度E的轴测投影长度为e x、e y、e z，它们与E之比，分别称为O1X1、O1Y1、O1Z1轴上的轴向伸缩系数，分别用p、q、r表示。

二、轴测图的分类按投影方向与轴测投影面的夹角，轴测图可分为：（1）正轴测图——轴测投影方向（投射线）与轴测投影面垂直时得到的轴测图。

（2）斜轴测图——轴测投影方向（投射线）与轴测投影面倾斜时得到的轴测图。

若按轴向伸缩系数的不同，轴测图又可分为（1）正（或斜）等测轴测图——p=q=r；（2）正（或斜）二测轴测图——p=r≠q；（3）正（或斜）三测轴测图——p≠q≠r；本书只介绍正等测图和斜二测图三、轴测图的基本性质由于轴测投影属于平行投影，因此轴测投影仍具有平行投影的基本性质：（1）物体上互相平行的线段，在轴测图中仍然互相平行。

（2）物体上与坐标轴平行的线段，在轴测图中也必定平行于相应的轴测轴。

且与相应的轴测轴有着相同的轴向伸缩系数。

熟练掌握与运用以上性质，既能迅速而正确地画出轴测图，又能方便地识别轴测图画法中的错误。

轴测投影的基本概念汇总

轴测投影的基本概念汇总
轴测轴上的线段长度与空间物体上对应线段长 度之比。
P
X 1 A1
C1
Z1
O1A1 OA O1B1 OB O1C1
= p X轴轴向变化率 = q Y轴轴向变化率 = r Z轴轴向变化率
O1
B1
Y1
C A O B
Z1
OC
X1
Y1
5
3. 轴测投影的性质
(1)空间相互平行的直线，它们的轴测投影也相互平行。 (2)物体上平行于坐标轴的线段,轴测投影仍与相应的 轴测轴平行。
P
特点: 物体与投影面倾斜 用正投影法
与投影面都处于倾斜位置，然后用正投影法作出物体的投影。
Z1
V
X'
Z' O'
Z
X1
X
O Y
Y1
Z1XΒιβλιοθήκη O YX1H
Y1
2
2)斜轴测图的形成 不改变原物体与投影面的相对位置，改变投 射线的方向，使投射线与投影面倾斜。
P
正投影图
Z S S0 Y
斜轴测投影图 Z1
P
X1 Z1
A1
O1 Y1
B1
Z1
A1B1=AB×p
A
B
X1
O
6
Y1
4.轴测图的分类
正等测 正轴测图 轴测图 斜轴测图 正二测 正三测 斜等测 斜二测 斜三测 p=q=r 两个轴向变化率相等 三个轴向变化率都不等 p=q=r 两个轴向变化率相等 三个轴向变化率都不等
正等测轴测图
斜二测轴测图
7
X
O
O1 X1 Y1
特点: 用斜投影法；物体正面与投影面平行
3
2 . 轴测图的基本参数
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
P
X1 Z1
A1
O1 Y1
B1
Z1
A1B1=AB×p
A
B
X1
O
6
Y1
4.轴测图的分类
正等测 正轴测图 轴测图 斜轴测图 正二测 正三测 斜等测 斜二测 斜三测 p=q=r 两个轴向变化率相等 三个轴向变化率都不等 p=q=r 两个轴向变化率相等 三个轴向变化率都不等
正等测轴测图
斜二测轴测图
7
P
特点: 物体与投影面倾斜 用正投影法
与投影面都处于倾斜位置，然后用正投影法作出物体的投影。
Z1
V
X'
Z' O'
Z
X1
X
O Y
Y1
Z1
X
O Y
X1
H
Y1
2
2)斜轴测图的形成 不改变原物体与投影面的相对位置，改变投 射线的方向，使投射线与投影面倾斜。
P
正投影图
Z S S0 Y
斜轴测投影图 Z1
轴测轴上的线段长度与空间物体上对应线段长 度之比。
P
X 1 A1
C1
Z1
O1A1 OA O1B1 OB O1C1
= p X轴轴向变化率 = q Y轴轴向变化率 = r Z轴轴向变化率
O1
B1
Y1
C A O B
Z1
OC
X1
Y1
5
3. 轴测投影的性质
(1)空间相互平行的直线，它们的轴测投影也相互平行。 (2)物体上平行于坐标轴的线段,轴测投影仍与相应的 轴测轴平行。
一、轴测投影基本概念
将物体连同其直角坐标系，沿不平行 于任一坐标面的方向，用平行投影法将其 投射在单一投影面上所得的具有立体感的 图形叫做轴测图。 投射方向垂直于轴测投影面 ——正轴测图。 投射方向倾斜于轴测投影面 ——斜轴测图。
1
1. 轴测图的形成
1)正轴测图的形成
复习多面正投影 改变物体和投影面的相对位置，使物体的正面、顶面和侧面
X
O
O1 X1 Y1
特点: 用斜投影法；物体正面与投影面平行
3
2 . 轴测图的基本参数
1)轴测投影面 2)轴测轴和轴间角
P
X1
坐标轴：OX，OY，OZ
轴测轴：O1X1，O1Y1，O1Z1
轴间角：X1O1Y1，X1O1Z1， Y1 O1 Z1
Z1
O1
Y1
Z1
O
4
X1
Y1
3)轴向变化率(轴向伸缩系数)