轴测图基本知识
- 格式:doc
- 大小:24.00 KB
- 文档页数:6






CAD教程第16章-轴测图的基本知识轴测图的基本知识一、轴测图的形成及投影特性用平行投影法将物体连同确定物体空间位置的直角坐标系一起投射到单一投影面,所得的投影图称为轴测图。
由于轴测图是用平行投影法得到的,因此具有以下投影特性:1、空间相互平行的直线,它们的轴测投影互相平行。
2、立体上凡是与坐标轴平行的直线,在其轴测图中也必与轴测轴互相平行。
3、立体上两平行线段或同一直线上的两线段长度之比,在轴测图上保持不变。
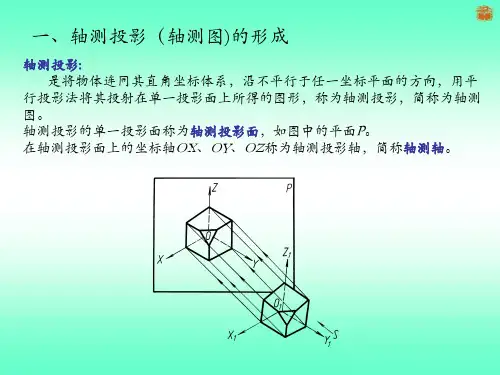
二、轴向伸缩系数和轴间角投影面称为轴测投影面。
确定空间物体的坐标轴OX、OY、OZ在P面上的投影O1X1、O1Y1、O1Z1称为轴测投影轴,简称轴测轴。
轴测轴之间的夹角∠X1O1Y1、∠Y1O1Z1、∠Z1O1X1称为轴间角。
由于形体上三个坐标轴对轴测投影面的倾斜角度不同,所以在轴测图上各条轴线长度的变化程度也不一样,因此把轴测轴上的线段与空间坐标轴上对应线段的长度比,称为轴向伸缩系数。
三、轴测图的分类轴测图分为正轴测图和斜轴测图两大类。
当投影方向垂直于轴测投影面时,称为正轴测图;当投影方向倾于轴测投影面时,称为斜轴测图。
由些可见:正轴测图是由正投影法得来的,而斜轴测图则是用斜投影法得来的。
正轴测图按三个轴向伸缩系数是否相等而分为三种:1、正等测图简称正等测:三个轴向伸缩系数都相等;2、正二测图简称正二测:只有两个轴向伸缩系数相等;3、正三测图简称正三测:三个轴向伸缩系数各不相等。
同样,斜轴测图也相应地分为三种:1、斜等测图简称斜等测:三个轴向伸缩系数都相等;2、斜二测图简称斜二测:只有两个轴向伸缩系数相等;3、斜三测图简称斜三测:三个轴向伸缩系数各不相等。
工程上用得较多的是正等测和斜二测。
本章只介绍这两种轴测图的画法。
作物体的轴测图时,应先选择画哪一种轴测图,从而确定各轴向伸缩系数和轴间角。
轴测轴可根据已确定的轴间角,按表达清晰和作图方便来安排,而Z轴常画成铅垂位置。
在轴测图中,应用粗实线画出物体的可见轮廓。




轴测图基本知识:
一、基本概念
1.将物体及所在的直角坐标系沿不平行于任一坐标面方向,用平行投影法投射在投影面上获得的立体图的图形。
2.轴测投影面:获得轴测投影的平面
3.轴测轴:将互相垂直的直角坐标轴投射在轴测投影面上的投影。
4.轴间角:轴测轴之间的夹角。
5.轴向伸缩系数:
轴测投影长/实际长=轴向伸缩系数
X方向为p,y方向为q,z方向为r
P平方+q平方+r平方=1
二、性质
1.空间线段平行则轴测投影平行
2.平行坐标轴的线段投影长=实长乘以该轴的轴向伸缩系数
三、分类
1.正轴测图:投射线与轴测投影面垂直
包括:正等轴测图p=q=r=0.82 轴间角120°简化系数为1
正二轴测图p =r q=0.47 一个轴间角97°10‘,另两个轴间角131°25‘
简化系数为p=r=1,q=0.5
正三轴测图p,q,r不相等
2.斜轴测:投射线与轴测投影面倾斜
斜等轴测图p=q=r
斜二轴测图p =r 一个轴间角90°,另两个轴间角135°
简化系数为p=r=1,q=0.5
坐标面与轴测投影面平行,与坐标面平行的形状,轴测图反映实形。
斜三轴测图p,q,r不相等。
教案首页第八章轴测图本章重点1)掌握轴测图的形成和基本作图原理。
2)掌握正等测的作图原理和作图方法3)掌握斜二测的作图原理和作图方法4)用CAD绘制轴测图本章难点1)掌握正等测和斜二测的作图方法2)掌握CAD绘制轴测图的方法本章要求1)已知物体的三视图,作其正等测立体图。
2)已知物体的三视图,作其斜二测立体图。
3)CAD绘制轴测图四、本章内容:§8-1 轴测图的基本知识一、轴测图的形成及投影特性用平行投影法将物体连同确定物体空间位置的直角坐标系一起投射到单一投影面,所得的投影图称为轴测图。
由于轴测图是用平行投影法得到的,因此具有以下投影特性:1、空间相互平行的直线,它们的轴测投影互相平行。
2、立体上凡是与坐标轴平行的直线,在其轴测图中也必与轴测轴互相平行。
3、立体上两平行线段或同一直线上的两线段长度之比,在轴测图上保持不变。
二、轴向伸缩系数和轴间角投影面称为轴测投影面。
确定空间物体的坐标轴OX、OY、OZ在P面上的投影O1X1、O1Y1、O1Z1称为轴测投影轴,简称轴测轴。
轴测轴之间的夹角∠X1O1Y1、∠Y1O1Z1、∠Z1O1X1称为轴间角。
由于形体上三个坐标轴对轴测投影面的倾斜角度不同,所以在轴测图上各条轴线长度的变化程度也不一样,因此把轴测轴上的线段与空间坐标轴上对应线段的长度比,称为轴向伸缩系数。
三、轴测图的分类轴测图分为正轴测图和斜轴测图两大类。
当投影方向垂直于轴测投影面时,称为正轴测图;当投影方向倾于轴测投影面时,称为斜轴测图。
由些可见:正轴测图是由正投影法得来的,而斜轴测图则是用斜投影法得来的。
正轴测图按三个轴向伸缩系数是否相等而分为三种:1、正等测图简称正等测:三个轴向伸缩系数都相等;2、正二测图简称正二测:只有两个轴向伸缩系数相等;3、正三测图简称正三测:三个轴向伸缩系数各不相等。
同样,斜轴测图也相应地分为三种:1、斜等测图简称斜等测:三个轴向伸缩系数都相等;2、斜二测图简称斜二测:只有两个轴向伸缩系数相等;3、斜三测图简称斜三测:三个轴向伸缩系数各不相等。
轴测图在工程上应用正投影法绘制的多面正投影图,可以完全确定物体的形状和大小,且作图简便,度量性好,依据这种图样可制造出所表示的物体。
但它缺乏立体感,直观性较差,要想象物体的形状,需要运用正投影原理把几个视图联系起来看,对缺乏读图知识的人难以看懂。
轴测图是一种单面投影图,在一个投影面上能同时反映出物体三个坐标面的形状,并接近于人们的视觉习惯,形象、逼真,富有立体感。
但是轴测图一般不能反映出物体各表面的实形,因而度量性差,同时作图较复杂。
因此,在工程上常把轴测图作为辅助图样,来说明机器的结构、安装、使用等情况,在设计中,用轴测图帮助构思、想象物体的形状,以弥补正投影图的不足。
多面正投影图与轴测图的比较如图5.0-1所示。
(a) 多面正投影图(b) 轴测图图5.0-1 多面正投影图与轴测图的比较5.1 轴测图的基本知识一、轴测图的形成轴测图是把空间物体和确定其空间位置的直角坐标系按平行投影法沿不行于任何坐标面的方向投影到单一投影面上所得的图形。
如图 5.1-1所示。
轴测图具有平行投影的所有特性。
例如:1.平行性: 物体上互相平行的线段,在轴测图上仍互相平行。
2.定比性: 物体上两平行线段或同一直线上的两线段长度之比,在轴测图上保持不变。
3.实形性: 物体上平行轴测投影面的直线和平面,在轴测图上反映实长和实形。
当投射方向S 垂直于投影面时,形成正轴测图;当投射方向S 倾斜于投影面时,形成斜轴测图。
图5.1-1 轴测图的形成二、轴测图的基本术语图5.1-2图5.1-3三、轴测图的特性由于轴测图是用平行投影法形成的,所以在原物体和轴测图之间必然保持如下关系:①若空间两直线互相平行,则在轴测图上仍互相平行。
②凡是与坐标轴平行的线段,在轴测图上必平行于相应的轴测轴,且其伸缩系数与相应的轴向伸缩系数相同。
凡是与坐标轴平行的线段,都可以沿轴向进行作图和测量,“轴测”一词就是“沿轴测量”的意思。
而空间不平行于坐标轴的线段在轴测图上的长度不具备上述特性。
四、轴测图的分类1、按投射方向分按投射方向对轴测投影面相对位置的不同,轴测图可分为两大类:①正轴测图:投射方向垂直于轴测投影面时,得到正轴测图,如图7-2 ( a )所示。
②斜轴测图:投射方向倾斜于轴测投影面时,得到斜轴测图,如图7-2 ( b )所示。
2、按轴向伸缩系数的不同分在上述两类轴测图中,按轴向伸缩系数的不同,每类又可分为三种:①正(或斜)等轴测图(简称正等测或斜等测):p 1 = q 1 = r 1 。
②正(或斜)二等轴测图(简称正二测或斜二测):p 1 =r 1 ≠ q 1 ,p 1=q 1 ≠ r 1 ,r 1 =q 1 ≠ p 1 。
③正(或斜)三轴测图(简称正三测或斜三测):p 1 ≠ q 1 ≠ r 1 。
国家标准GB/T 14692-1993 中规定,一般采用正等测、正二测、斜二测三种轴测图,工程上使用较多的是正等测和斜二测,本章主要介绍这两种轴测图的画法。
一、轴测图的形成将物体连同其参考直角坐标系沿不平行于任一坐标面的方向,用平行投影法将其投射在单一投影面上所得到的图形称为轴测图。
如图9-1-1-1所示,用正投影法形成的轴测图称为正轴测图;用斜投影法形成的轴测图称为斜轴测图。
由于轴测图能同时反映出物体长、宽、高三个方向的尺度,尽管物体的一些表面形状有所改变,但仍富有立体感,所以轴测图常用作帮助读图的辅助性图样。
图9-1-1-1 轴测图的形成多面正投影图能够准确而完整地表达物体的形状和大小,可量性好,而且作图简便,如图9-1-1-2(a)所示,因而在机械制造、工程建设中得到广泛使用。
但是,它缺乏立体感,直观性差。
为了弥补它的不足,工程上常采用轴测投影图作为辅助图样,来帮助理解较复杂的结构,在设计中也可以借助于轴测图更有效地进行空间构思。
如图9-1-1-2(b)所示,即为如图9-1-1-2(a)所示中物体的轴测投影图(简称轴测图),其直观性强,但作图过程较繁,度量性差。
图9-1-1-2 多面正投影图与轴测图的比较二、轴测图的相关术语1. 轴测投影面得到轴测投影的平面,称为轴测投影面,一般用字母P表示。
2. 轴测轴直角坐标体系的坐标轴O0X0、O0Y0、O0Z0在轴测投影面P上的投影OX、OY、OZ称为轴测轴,简称X轴、Y轴、Z轴。
3. 轴间角每两个轴测轴间的夹角,称为轴间角,即:<XOY、<XOZ、<YOZ< p>4. 轴向伸缩系数轴测轴上的单位长度与相应空间直角坐标轴上的单位长度之比,称为轴向伸缩系数。
X、Y、Z方向的轴向伸缩系数分别用p、q、r表示。
如图9-1-1-1所示,设空间O0X0轴上单位长度为O0A0,其相应轴测轴上的单位长度则为OA,则有X轴向伸缩系数:p= OA/O0A0同理,可得到Y轴向伸缩系数和Z轴向伸缩系数。
三、轴测投影的基本特性由于轴测投影属于平行投影,因此它具有平行投影的全部特性,以下几点基本特性在绘制轴测图时经常使用,应熟练掌握和运用。
1. 物体上相互平行的两条直线的轴测投影仍相互平行。
同理,物体上与坐标轴平行的直线,在轴测图中也必定与相应的轴测轴平行。
2. 空间同一线段上各段长度之比在轴测投影图中保持不变。
3. 沿坐标轴的轴向长度可以按伸缩系数进行度量。
由于平行线的轴测投影仍互相平行,因此,物体上凡是平行于O0X0、O0Y0、O0Z0轴的线段,其轴测投影必须相应平行于OX、OY、OZ轴,且具有和OX、OY、OZ轴相同的轴向伸缩系数。
在轴测图中,只有沿轴测轴方向才可以测量长度,这就是"轴测"二字的含义。
请注意:与坐标轴不平行的线段具有与之不同的伸缩系数,不能直接测量与绘制,只能按"轴测"原则,根据端点坐标,作出两端点后连线绘出。
四、轴测图的分类根据投影方向不同,轴测图可分为两类,即正轴测图和斜轴测图。
根据轴向伸缩系数不同,轴测图又可分为等测、二测和三测轴测图。
以上两种分类方法相结合,可得到六种轴测图。
1. 正轴测投影(投影方向垂直于轴测投影面)(1) 正等轴测投影(简称正等测):轴向伸缩系数p=q=r。
(2) 正二等轴测投影(简称正二测):轴向伸缩系数p=r=2q。
(3) 正三测轴测投影(简称正三测):轴向伸缩系数p≠q≠r。
2. 斜轴测投影(投影方向倾斜于轴测投影面)(1) 斜等轴测投影(简称斜等测):轴向伸缩系数p=q=r。
(2) 斜二等轴测投影(简称斜二测):轴向伸缩系数p=r=2q。
(3) 斜三测轴测投影(简称斜三测):轴向伸缩系数p≠q≠r。
工程上主要使用正等测和斜二测,本章也只介绍这两种轴测图的画法。
五、轴测图的基本作图方法和基本作图步骤1. 基本作图方法轴测图的基本作图方法有坐标法、叠加法和切割法,其中坐标法是基。
(1) 坐标法对较简单的物体,可根据物体上一些关键点(如平面立体的顶点、曲线上的控制点)的坐标值作出这些点的轴测投影,再依次连线成图。
(2) 切割法对较复杂的物体,用形体分析法可将其看成是由一个形状简单的基本体逐步切割而成,先画出该简单形体的轴测图,再在其上逐步切割。
(3) 叠加法对较复杂立体,用形体分析法可将其看成是由几个简单的基本体叠加而成,把这些基本体的轴测图按照相对位置关系叠加即可得到整个物体的轴测图。
2. 基本作图步骤绘制物体的轴测图时,应先选择确定要画哪种轴测图,从而确定各轴间角和轴向伸缩系数。
轴测图可根据已确定的轴间角,咱按表达清楚和作图方便来安排,画出坐标原点和轴测轴,一般Z轴常画出铅垂位置。
利用三种基本作图方法逐个画出各顶点或线段,用粗实线画出物体的可见轮廓线,在轴测图中,为了使画出的图形明显起见,且为了增强立体感,通常不画出物体的不可见轮廓线,但在一、轴测图的形成将物体连同其参考直角坐标系沿不平行于任一坐标面的方向,用平行投影法将其投射在单一投影面上所得到的图形称为轴测图。
如图9-1-1-1所示,用正投影法形成的轴测图称为正轴测图;用斜投影法形成的轴测图称为斜轴测图。
由于轴测图能同时反映出物体长、宽、高三个方向的尺度,尽管物体的一些表面形状有所改变,但仍富有立体感,所以轴测图常用作帮助读图的辅助性图样。
图9-1-1-1 轴测图的形成多面正投影图能够准确而完整地表达物体的形状和大小,可量性好,而且作图简便,如图9-1-1-2(a)所示,因而在机械制造、工程建设中得到广泛使用。
但是,它缺乏立体感,直观性差。
为了弥补它的不足,工程上常采用轴测投影图作为辅助图样,来帮助理解较复杂的结构,在设计中也可以借助于轴测图更有效地进行空间构思。
如图9-1-1-2(b)所示,即为如图9-1-1-2(a)所示中物体的轴测投影图(简称轴测图),其直观性强,但作图过程较繁,度量性差。
图9-1-1-2 多面正投影图与轴测图的比较二、轴测图的相关术语1. 轴测投影面得到轴测投影的平面,称为轴测投影面,一般用字母P表示。
2. 轴测轴直角坐标体系的坐标轴O0X0、O0Y0、O0Z0在轴测投影面P上的投影OX、OY、OZ称为轴测轴,简称X轴、Y轴、Z轴。
3. 轴间角每两个轴测轴间的夹角,称为轴间角,即:<XOY、<XOZ、<YOZ< p>4. 轴向伸缩系数轴测轴上的单位长度与相应空间直角坐标轴上的单位长度之比,称为轴向伸缩系数。
X、Y、Z方向的轴向伸缩系数分别用p、q、r表示。
如图9-1-1-1所示,设空间O0X0轴上单位长度为O0A0,其相应轴测轴上的单位长度则为OA,则有X轴向伸缩系数:p= OA/O0A0同理,可得到Y轴向伸缩系数和Z轴向伸缩系数。
三、轴测投影的基本特性由于轴测投影属于平行投影,因此它具有平行投影的全部特性,以下几点基本特性在绘制轴测图时经常使用,应熟练掌握和运用。
1. 物体上相互平行的两条直线的轴测投影仍相互平行。
同理,物体上与坐标轴平行的直线,在轴测图中也必定与相应的轴测轴平行。
2. 空间同一线段上各段长度之比在轴测投影图中保持不变。
3. 沿坐标轴的轴向长度可以按伸缩系数进行度量。
由于平行线的轴测投影仍互相平行,因此,物体上凡是平行于O0X0、O0Y0、O0Z0轴的线段,其轴测投影必须相应平行于OX、OY、OZ轴,且具有和OX、OY、OZ轴相同的轴向伸缩系数。
在轴测图中,只有沿轴测轴方向才可以测量长度,这就是"轴测"二字的含义。
请注意:与坐标轴不平行的线段具有与之不同的伸缩系数,不能直接测量与绘制,只能按"轴测"原则,根据端点坐标,作出两端点后连线绘出。
四、轴测图的分类根据投影方向不同,轴测图可分为两类,即正轴测图和斜轴测图。
根据轴向伸缩系数不同,轴测图又可分为等测、二测和三测轴测图。
以上两种分类方法相结合,可得到六种轴测图。