点三次Hermite插值多项式

数值分析误差限的计算公式1、误差x∗为 x 一个近似值绝对误差：e∗=x∗−x相对误差：e∗r=e∗x=x∗−xx，由于真值 x 总是不知道的，通常取e∗r=e∗x∗=x∗−xx∗误差限：|x∗−x|≤ε∗相对误差限：ε∗r=ε∗|x∗|ε(f(x∗))≈|f′(x∗)|ε(x∗)2、插值法记ωn+1(x)=(x−x0)(x−x1)⋯(x−xn)Lagrange 插值多项式系数：lk(xk)=(x−x0)⋯(x−xk−1)(x−xk+1)⋯(x−xn)(xk−x0)⋯(xk−xk−1)(x −xk+1)⋯(x−xn)Lagrange 插值多项式：Ln(x)=∑k=0nlk(x)yk=∑k=0nykωn+1(x)ω′n+1(xk)(x−xk) 余项：记 Mn+1=maxa≤x≤b|fn+1(x)|R(x)=fn+1(ξ)ωn+1(x)(n+1)!≤Mn+1(n+1)!|ωn+1(x)|均差与 NewTon 插值多项式一阶均差：f[x0,xk]=f(xk)−f(x0)xk−x0k 阶均差：f[x0,x1,⋯,xk]=f[x0,⋯,xk−2,xk]−f[x0,⋯,xk−2,xk−1]xk−xk−1f[x0,x1,⋯,xn]=f(n)(ξ)n!(x0,x1,⋯,xn,ξ∈[a,b])f[x0,x1,⋯,xk]=∑j=0kf(xj)ω′k+1(xj)NewTon 插值多项式：Pn(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn−1)余项：R(x)=f[x0,x1,⋯,xn]ωn+1(x)Hermite 插值Taylor 多项式：Pn(x)=f(x0)+f′(x0)(x−x0)+⋯+f(n)(x0)n!(x−x0)n余项：R(x)=f(n+1)(ξ)(n+1)!(x−x0)n+1若已知 f(x0),f′(x1),f(x1),f(x2)：P(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+A(x−x0)(x−x1)(x−x2)其中 A 由 P′(x1)=f′(x1) 可得余项：R(x)=14!f(4)(ξ)(x−x0)(x−x1)2(x−x2)两点三次 Hermite 插值多项式：H3(x)=αk(x)yk+αk+1(x)yk+1+βk(x)mk+βk+1(x)mk+1其中 mk=f′(xk),mk+1=f′(xk+1)⎧⎧⎧⎧⎧⎧⎧⎧⎧⎧⎧αk(x)=(1+2x−xkxk+1−xk)(x−xk+1xk−xk+1)2αk+1(x)=(1+2x−xk+1xk−xk+1)(x−xkxk+1−xk)2⎧⎧⎧⎧⎧⎧⎧⎧⎧⎧⎧βk(x)=(x−xk)(x−xk+1xk−xk+1)2βk+1(x)=(x−xk+1)(x−xkxk+1−xk)2余项：R(x)=f(4)(ξ)4!(x−xk)2(x−xk+1)2分段低次插值h=b−an对每个小区间使用对应插值公式求 Ih(x)余项对分段线性插值函数：maxa≤x≤b|f(x)−Ih(x)|≤M28h2对分段三次埃尔米特插值：maxa≤x≤b|f(x)−Ih(x)|≤M4384h43、数值积分代数精度定义：如果某个求积公式对于次数不超过 m 的多项式均能够准确成立，但对于 m+1 次多项式就不准确成立，则称该公式具有 m 次代数精度梯形公式公式与中矩形公式梯形公式：∫baf(x)dx≈b−a2f(a)+b−a2f(b)余项：R[f]=−(b−a)312f′′(η)(η∈(a,b))矩形公式：∫baf(x)dx≈(b−a)f(a+b2)余项：R[f]=(b−a)324f′′(η)(η∈(a,b))Newton-Cotes 公式将积分区间 [a,b] 分成 n 等分Simpson 公式（n=2）：∫baf(x)dx≈b−a6f(a)+b−a6f(b)+2(b−a)3f(a+b2)余项：R[f]=−(b−a)5180∗24f(4)(η)(η∈(a,b))Cotes 公式（n=4）：C=b−a90[7f(x0)+32f(x1)+12f(x2)+32f(x3)+7f(x4)]余项：R[f]=−2(b−a)7945∗46f(6)(η)(η∈(a,b))复合求积公式积分区间 [a,b] 分成 n 等分，步长 h=b−an复合梯形公式：Tn=h2[f(a)+2∑k=0n−1f(xk)+f(b)]余项：Rn(f)=−b−a12h2f′′(η)复合 Simpson 求积公式：Sn=h6[f(a)+2∑k=0n−1f(xk)+4∑k=1n−2f(x(k+1)/2)+f(b)] 其中 x(k+1)/2=xk+h2Rn(f)=−b−a180(h2)4f(4)(η)龙贝格求积算法T(0)0=h2[f(a)+f(b)]求梯形值 T0(b−a2k)，利用递推公式求 T(k)0，递推公式：T2n=12Tn+h2∑k=0n−1f(xk+12)求加速值：T(k)m=4m4m−1Tk+1m−1−14m−1T(k)m−1k=1,2,⋯高斯-勒让德求积公式积分区间为 [−1,1]∫1−1f(x)dx≈∑k=0nAkf(xk)余项：n=1 时，R1[f]=1135f(4)(η)4、解线性方程组的直接方法列主元高斯消去法在每次消元时，选取列主元在最前面，列主元为该列最大值矩阵三角分解法如果 n 阶矩阵 A 的各阶顺序主子式 Dk(k=1,2,⋯,n−1) 均不为零，则必有单位下三角矩阵 L 和上三角矩阵 U，使得 A=LU，并且 L 和 U 是唯一的。

分段三次hermite函数
分段三次 Hermite 函数是一种用于插值数据、拟合数据以及数值微分的函数。

它的特点是可以通过选择足够的基函数来适应各种不同的非线性函数。

本文将深入探讨分段三次 Hermite 函数的定义、应用和优点。

一、定义
分段三次 Hermite 函数是一种三次多项式函数。

它由基函数和插值条件构成。

1. 基函数
1）常数项
2）线性项
3）二次项
这些基函数可以用于构建分段三次 Hermite 函数，使其适应不同的非线性函数。

2. 插值条件
1）值的匹配条件
二、应用
分段三次 Hermite 函数广泛应用于数值微分、插值和拟合。

下面将分别介绍这些应用。

分段三次 Hermite 函数可以用于插值数据。

通过确定插值条件，可以得到一个分段三次 Hermite 函数，使其在给定数据点处与目标函数匹配。

这种方法常常用于构建数值框架，如数值微分和数值积分。

3. 拟合
三、优点
1. 精确度高
2. 稳定性高
分段三次 Hermite 函数具有优良的稳定性。

它可以处理大量的数据，而不会出现精度问题或数值不稳定性。

3. 方便性高
4. 可扩展性高
分段三次 Hermite 函数具有非常强的可扩展性。

它可以扩展到高维空间，适应各种不同的数据类型，从而得到非常精确的结果。

在第一个插值点上的hermite三点插
指公式
在第一个插值点上的hermite三点插指公式
Hermite三点插值法是一种采用三个插值点来求解函数f(x)在给定范围内的曲
线图的插值算法，通常是用来拟合y=f(x)在离散中提供的三个点的插值函数，在
第一个插值点的提出的这种特定的三点插值模型，即对第一个插值点位置
(x0,f(x0))，其中x0为插值点位置，f(x0)为其处的函数值，用的三点模型可写为：
f(x)=f(x0)+f'(x0)(x-x0)+[f''(x0)/2](x-x0)^2
即，把第一个插值点位置(x0,f(x0))处的点代入，可以得到其相应的函数拟合
多项式，当然，并不是每一个函数拟合多项式都能满足实际需求，这就需要注意函数拟合多项式的拟合度，可以在参数估计和函数估计的时候，使用一定的误差来估计函数值，从而获得函数拟合度较好的模型。

此外，在使用Hermite三点插值法时，需要注意三个点之间的位置关系，三个
点位于x0，x1，x2等位置，在确定每个点的位置时应该考虑到它们之间的距离，
一般来说，三个点之间的间距应保持一定，以使插值函数尽可能精确的反映函数的实际变化。

因此，要使得Hermite三点插值法能取得较好的效果，在确定三个插值点的位
置的时候要综合考虑它们之间的位置关系，以及在第一个插值点的估计时要注意拟合度，这样就能很好的进行三点插值，从而得到准确的结果。

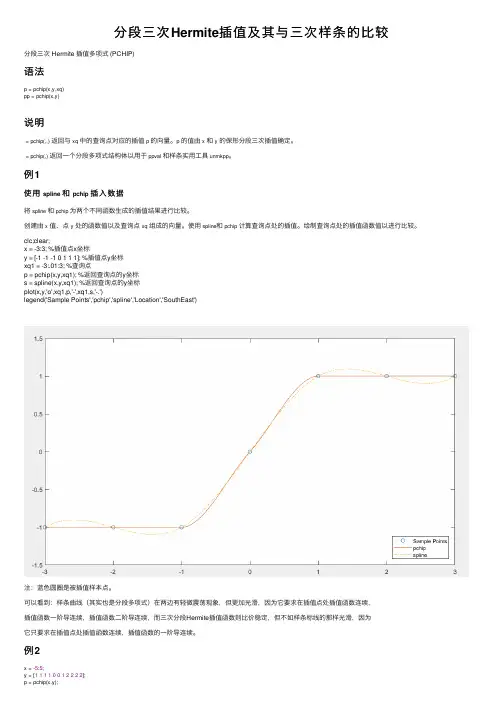
分段三次Hermite插值及其与三次样条的⽐较分段三次 Hermite 插值多项式 (PCHIP)语法p = pchip(x,y,xq)pp = pchip(x,y)说明= pchip(,,)返回与xq中的查询点对应的插值p的向量。

p的值由x和y的保形分段三次插值确定。

= pchip(,)返回⼀个分段多项式结构体以⽤于ppval和样条实⽤⼯具unmkpp。

例1使⽤spline和pchip插⼊数据将spline和pchip为两个不同函数⽣成的插值结果进⾏⽐较。

创建由x值、点y处的函数值以及查询点xq组成的向量。

使⽤spline和pchip计算查询点处的插值。

绘制查询点处的插值函数值以进⾏⽐较。

clc;clear;x = -3:3; %插值点x坐标y = [-1 -1 -1 0 1 1 1]; %插值点y坐标xq1 = -3:.01:3; %查询点p = pchip(x,y,xq1); %返回查询点的y坐标s = spline(x,y,xq1); %返回查询点的y坐标plot(x,y,'o',xq1,p,'-',xq1,s,'-.')legend('Sample Points','pchip','spline','Location','SouthEast')注：蓝⾊圆圈是被插值样本点。

可以看到：样条曲线（其实也是分段多项式）在两边有轻微震荡现象，但更加光滑，因为它要求在插值点处插值函数连续，插值函数⼀阶导连续，插值函数⼆阶导连续，⽽三次分段Hermite插值函数则⽐价稳定，但不如样条标线的那样光滑，因为它只要求在插值点处插值函数连续，插值函数的⼀阶导连续。

例2x = -5:5;y = [11110012222];p = pchip(x,y);xq = -5:0.2:5;pp = ppval(p,xq); %返回插值函数的查询点处的y坐标plot(x,y,'o',xq,pp,'-.')ylim([-0.22.2])例3x = -5:5;y = [11110012222];p = pchip(x,y);s = spline(x,y);xq = -5:0.1:5;pp = ppval(p,xq); %返回插值函数的查询点处的y坐标ss = ppval(s,xq); %返回插值函数的查询点处的y坐标figure(1);hold on;plot(x,y,'o',xq,pp,'-.',xq,ss,'b-')ylim([-0.22.2])figure(1);hold on ;legend('Sample Points','分段三次Hermite','分段三次样条','Location','SouthEast')PCHIP是分段三次hermit插值，但书中的该⽅法必须知道点的值和导数值，为什么PCHIP的变量只有函数值⽽没有导数值？在⽤pchip插值的过程中，matlab会基于所给的函数值来帮你估算各导数值。

hermite三点插指公式的插值基法hermite三点插入法的插值基法概述Hermite三点插入法是一种常用的插值方法，它使用三点来构造插值变换，这三点的x坐标满足X_0 <= X_1 < X_2，插值变换的控制点是(X_0,Y_0)、(X_1,Y_1)和(X_2,Y_2)，而且这三点之间的平均斜率值也是已知的。

根据这三点的信息，可以构造出插值变换的具体形式，从而可以用于插值计算。

原理Hermite三点插入法实际上是基于Hermite多项式插值的，要构造出插值变换的具体形式，需要同时考虑到给定的两个控制点和满足Hermite多项式条件的两个切线斜率，具体构造的步骤如下：1）首先，建立插值函数：F(x)=a_0+a_1(x-x_0)+a_2(x-x_0)(x-x_1)+a_3(x-x_0)(x-x_1)(x-x _2)2）确定a_0,a_1,a_2,a_3的值，这是满足Hermite多项式条件的比较核心的步骤，有4个未知量，3个方程：F(x_0)=y_0 , F(x_1)=y_1 , F(x_2)=y_2另外两个方程是：F'(x_0)=(y_1-y_0)/(x_1-x_0) ,F'(x_2)=(y_2-y_1)/(x_2-x_1)3）使用求解某个系数的公式进行求解，求得四个系数：a_0=y_0a_1=(y_1-y_0)/(x_1-x_0)-(x_2-x_0)(y_2-y_0)/(x_2-x_1)(x_1-x_ 0)a_2=(x_2-x_1)(y_2-y_0)/(x_2-x_1)(x_1-x_0)a_3=(x_2-x_1)(x_2-x_0)(y_2-y_1)/(x_2-x_1)(x_1-x_0) 应用Hermite三点插入法可以用于插值计算，在计算机图形学中它也是一种常用的绘图方法。

一般来说，它可以用于函数图像的渲染、曲线的插值、多维函数的插值等方面。

它可以提高函数图像的平滑度，使图像看起来更加美观，还可以减少绘图的复杂度，在某些情况下可以提高绘图效率。

代码实现分段三次 hermite 插值多项式以下是 Python 代码实现分段三次 Hermite 插值多项式：```python。

import numpy as np。

def hermite_interpolation(x, y, dy):。

"""。

分段三次 Hermite 插值多项式。

:param x: 自变量数组。

:param y: 因变量数组。

:param dy: 导数数组。

:return: 插值函数。

"""。

n = len(x) - 1。

h=x[1:]-x[:-1]#计算每个区间的步长。

a=y[:-1]#a[i]表示第i个节点的函数值。

b = dy[:-1] # b[i] 表示第 i 个节点的导数值。

c = (3 * (y[1:] - y[:-1]) / h - 2 * dy[:-1] - dy[1:]) / h # 计算 c[i]。

d = (2 * (y[:-1] - y[1:]) + dy[:-1] + dy[1:]) / h ** 2 # 计算 d[i]。

def f(x0):。

#找到x0属于哪个区间。

i = np.searchsorted(x, x0) - 1。

#判断x0是否在所求区间内。

if i < 0 or i >= n:。

raise ValueError("x0 不在所求区间内")。

t=(x0-x[i])/h[i]。

# 分段 Hermite 插值多项式。

p=(1+2*t)*((1-t)*a[i]+t*a[i+1])+t*(t-1)*h[i]*c[i]。

p=p+t*(t-1)**2*h[i]**2*d[i]#注意加括号。

return p。

return f。

```。

代码中用到了 NumPy 库中的 `searchsorted` 函数，它可以用来找到一个数在一个有序数组中的位置。

具体使用方法可以参考其官方文档。

两点三次hermite插值c++程序例题两点三次Hermite插值是一种数值分析方法，用于在给定的数据点之间估计函数值。

这种方法基于多项式插值，并使用导数信息来提高插值的准确性。

以下是一个C++程序，实现了两点三次Hermite插值：cpp#include <iostream>#include <vector>// 定义一个结构体，用于存储数据点和它们的导数struct Point {double x;double y;double dy;};// 计算两点之间的差值double difference(double a, double b) {return a - b;}// 计算两点之间的差值的平方double squareDifference(double a, double b) {return difference(a, b) * difference(a, b);}// 计算两点之间的差值的立方double cubeDifference(double a, double b) {return squareDifference(a, b) * difference(a, b);}// 两点三次Hermite插值函数double hermiteInterpolation(const std::vector<Point>& points, double x) {double result = 0.0;for (size_t i = 0; i < points.size(); ++i) {double term = points[i].y;double prod = 1.0;for (size_t j = 0; j < points.size(); ++j) {if (i != j) {double weight = cubeDifference(x, points[j].x) / (squareDifference(points[i].x, points[j].x) *squareDifference(x, points[i].x));prod *= weight;}}result += term * prod;}return result;}int main() {std::vector<Point> points = {{1.0, 2.0, 3.0},{2.0, 3.0, 4.0},{3.0, 5.0, 6.0},{4.0, 7.0, 8.0}};double x = 2.5;double y = hermiteInterpolation(points, x);std::cout << "The interpolated value at x = " << x << " is y = " << y << std::endl;return 0;}这个程序首先定义了一个结构体`Point`，用于存储数据点及其导数。

分段三次 hermite 插值多项式的数学表达Hermite插值多项式是一种用于在给定的点集上进行插值的数学工具。

与其他插值方法不同的是，Hermite插值多项式不仅考虑了函数在各个插值点上的函数值，还考虑了函数在该点上的导数值。

这使得Hermite插值多项式能够更准确地拟合函数的曲线特征，特别是在存在函数奇点或不连续点的情况下。

要理解Hermite插值多项式的具体数学表达，首先需要了解插值点和插值条件的概念。

设给定的插值点集为{(x0, f0, f'0), (x1, f1, f'1), ..., (xn, fn, f'n)}，其中xi为插值点的横坐标，fi为插值点的纵坐标，f'i为插值点的导数值。

我们的目标是构造一个多项式P(x)，满足以下条件：1.在每个插值点(xi, fi)处，多项式P(x)的函数值等于fi：P(xi) = fi；2.在每个插值点(xi, fi)处，多项式P(x)的导数值等于f'i：P'(xi) = f'i。

根据这些插值条件，我们可以得到Hermite插值多项式的数学表达式。

首先，我们需要定义一个Lagrange插值基函数Lk(x)，用于描述在插值点xi处的多项式P(x)的函数值。

Lagrange插值基函数可以通过以下公式计算得到：Lk(x) = Π(j ≠ k) [(x - xj) / (xk - xj)]其中Π是乘积符号，j和k分别表示插值点的索引。

然后，我们可以构造Hermite插值多项式Hk(x)，它的数学表达式可以通过Lagrange插值基函数和插值点的函数值、导数值得到：Hk(x) = [1 - 2(x - xi)L'i(xi)]Li(x)^2 + (x - xi)Li(x)^2 其中Li(x)表示第i个插值点处的Lagrange插值基函数，L'i(xi)表示第i个插值点处的Lagrange插值基函数的导数值。

例若()f x 在[a,b]上有三阶连续导数，且已知()f x 在[,]a b 上两个互异的 点01,x x 上的函数值01(),()f x f x 和一阶导数值'0()f x ，试求满足条件 ''001100()(),()(),()()H x f x H x f x H x f x ===的插值多项式，并估计误差。

解由给定的3 个插值条件，显然可确定一个次数不超过2次的埃尔米特插值多项式()H x ， 又有()H x 应满足插值条件()()i i H x f x =，(0,1)i =，而节点01,x x 上的线性插值函数1()N x 也满足插值条件1()(),(0,1)i iN x f x i ==，故可设1()()()()H x N x A x x x x-=--，其中A 为待定常数，上式又可记为 101000101()()()()()()[,]()()H x N x A x x x x f x x x f x x A x x x x =+--=+-+--为了确定常数A ，对上式求导，得'0110()[,][()()]H x f x x A x x x x =+-+-，令0x x =代入，且注意插值条件''001010()[,]()()H x f x x A x x f x =+-=, 于是有'01010[,]()f x x f x A x x -=-，即()H x 为'010********[,]()()()()[,]()()f x x f x H x f x x x f x x x x x x x x -=+-+---，当然也可先采用拉格朗日多项式构造，同样得到满足相同条件的插值多项式()H x余项为(3)201()()()()6fR x x x x x ξ=--。

两点三次hermite插值例题Hermite插值是一种数值分析方法，用于在给定的数据点上生成一个多项式函数，以便通过这些数据点来近似描述一个函数。

Hermite插值是利用函数值和导数值来进行插值的一种方法，它可以更精确地逼近给定的数据点。

下面我将通过一个例题来说明Hermite插值的过程。

假设我们有以下数据点，(1, 2), (1, 3), (2, 1), (2, 2)，我们要使用Hermite插值来找到通过这些点的多项式函数。

首先，我们需要计算每个数据点的导数值。

因为数据点中有重复的x值，我们需要分别计算每个x值对应的导数值。

对于数据点(1, 2)和(1, 3)，我们可以假设它们对应的导数值分别为2和3；对于数据点(2, 1)和(2, 2)，我们可以假设它们对应的导数值分别为1和2。

接下来，我们将使用这些数据点和导数值来构建Hermite插值多项式。

Hermite插值多项式的一般形式为：\[P(x) = \sum_{i=0}^{n}f[x_0, x_1, \ldots, x_i](x-x_0)(x-x_1)\ldots(x-x_{i-1}) + \sum_{i=0}^{n}f[x_0, x_1,\ldots, x_i, x_i](x-x_0)(x-x_1)\ldots(x-x_{i-1})^2\]其中，\[f[x_0, x_1, \ldots, x_i]\]表示数据点\[x_0, x_1, \ldots, x_i\]处的插值函数值。

这个式子的第一部分表示通过数据点的函数值进行插值，第二部分表示通过数据点的导数值进行插值。

我们可以根据给定的数据点和导数值，计算出Hermite插值多项式。

最终得到的多项式函数就是通过这些数据点进行Hermite插值得到的结果。

总结起来，Hermite插值是一种利用函数值和导数值进行插值的方法，可以更精确地逼近给定的数据点。

通过计算数据点的导数值和使用Hermite插值多项式的公式，我们可以得到一个通过这些数据点的多项式函数。