专题训练(四) 根据二次函数的图象确定字母系数以及代数式的符号或数值

二次函数的图像和性质确定a 、b 、c 及相关代数式的符号符号的确定1、确定a 、b 、c 的符号(1)二次函数：c bx ax y ++=2，a 的符号由________决定； (2) 2-b a 的符号由________决定，结合a 的符号，可确定______的符号； (3)c 的符号由_____决定，当抛物线与y 轴交点在y 轴的正半轴时，c _____，当抛物线与y 轴交点在y 轴的负半轴时，c ______。

(4)确定了a 、b 、c 的符号，易确定abc 的符号。

2、确定类似代数式a +b +c 的符号当x =1时， y =a +b +c 。

因此代数式a +b +c 的符号______决定；与之类似的还经常出现判断a －b +c 、4a ±2b +c 、9a ±3b +c 等等的符号。

3、由对称轴x =2b a-的确定值判断a 与b 的关系 涉及到2a 和b 的代数式时常考虑对称轴a b x 2-=的位置情况。

如：12=-a b 能得到出：b a 21-=， 即21+=a b 。

4、与抛物线的对称轴有关的一些值的符号根据抛物线的对称性可知：取到对称轴距离相等的两个不同的x 值时，y 值相等，即当m ab x +-=2或m a b x --=2时，y 值相等。

5、24-b ac 的符号：24-b ac 的符号由抛物线与x 轴交点个数决定。

6、判断在同一坐标系中两种不同的图形的正误。

如：在同一种坐标系中正确画出一次函数y ax b =+和二次函数c bx ax y ++=2，关键是两个式子中的a 、b 值应相同。

例题教学例1、如图，给出八个结论：①a ＞0；②b ＞0；③c ＞0； ④a +b +c =0；⑤abc ＜0；⑥2a +b ＞0；⒄a +c =1；④a ＞1．其中正确的结论的序号是 ____________ 。

例2、一足球队员在距离球门12米处挑射，正好射中了2．4米高的球门横梁，若足球运动路线是抛物线c bx ax y ++=2如图，则下列结论：④601-<a ，④0601<<-a ，④a －b +c >0，④a <b <－12a 正确的结论是（ ） A ．④④ B ． ④④ C ． ④④ D ． ④④例3、已知抛物线c bx ax y ++=2 (a <0)经过点(－1，0)且满足4a +2b +c >0以下结论：④a +b >0，④a +c >0，④－a +b +c >0，④b 2－2ac >5a 2其中正确的个数有 （ ）A ．1个B ．2个C ．3个D ．4个课堂反馈1、已知二次函数c bx ax y ++=2图象与x 轴交于(－2，0)(x ，0)且1<x 1<2，与y 轴正半轴交点在(0，2)下方，下列结论，④a <b <0，④2a +c >0，④4a +c <0，④2a －b +1>0其中正确个数为 ( )A ．1个B ．2个C ．3个D ．4个2、已知a <－1，点（a －1，y 1），（a ，y 2），（a +1，y 2）都在函数y =x 2的图象上，则（ ）A ．y 1<y 2<y 3B ．y 1<y 3<y 2C ．y 3<y 2<y 1D ．y 2<y 1<y 33、二次函数c bx ax y ++=2的图象如图，有下列5个结论：④ 0>abc ；④ c a b +<；④ 024>++c b a ；④ b c 32<；⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有 个。

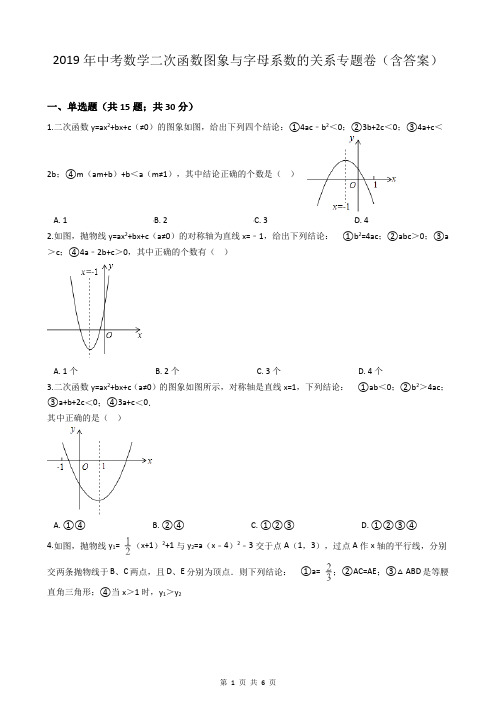
2019年中考数学二次函数图象与字母系数的关系专题卷（含答案）一、单选题（共15题；共30分）1.二次函数y=ax2+bx+c（≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②3b+2c＜0；③4a+c＜2b；④m（am+b）+b＜a（m≠1），其中结论正确的个数是（）A. 1B. 2C. 3D. 42.如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，给出下列结论：①b2=4ac；②abc＞0；③a ＞c；④4a﹣2b+c＞0，其中正确的个数有（）A. 1个B. 2个C. 3个D. 4个3.二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，下列结论：①ab＜0；②b2＞4ac；③a+b+2c＜0；④3a+c＜0．其中正确的是（）A. ①④B. ②④C. ①②③D. ①②③④4.如图，抛物线y1= （x+1）2+1与y2=a（x﹣4）2﹣3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：①a= ；②AC=AE；③△ABD是等腰直角三角形；④当x＞1时，y1＞y2其中正确结论的个数是（）A. 1个B. 2个C. 3个D. 4个5.已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：①抛物线过原点；②4a+b+c=0；③a﹣b+c＜0；④抛物线的顶点坐标为（2，b）；⑤当x＜2时，y随x增大而增大．其中结论正确的是（）A. ①②③B. ③④⑤C. ①②④D. ①④⑤6.一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示，则二次函数y=ax2+bx+c 的图象可能是（）A. B. C. D.7.二次函数y=ax2+bx+c（a、b、c是常数，且a≠0）的图象如图所示，下列结论错误的是（）A. 4ac＜b2B. abc＜0C. b+c＞3aD. a＜b8.如图所示，抛物线y=ax2+bx+c的顶点为B（﹣1，3），与x轴的交点A在点（﹣3，0）和（﹣2，0）之间，以下结论：①b2﹣4ac=0；②a+b+c＞0；③2a﹣b=0；④c﹣a=3其中正确的有（）A. 1B. 2C. 3D. 49.已知二次函数y=ax2+bx+c的图象如下，则一次函数y=ax﹣2b与反比例函数y= 在同一平面直角坐标系中的图象大致是（）A. B. C. D.10.如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（）A. ①③B. ②③C. ②④D. ②③④之间，其部分图象如图所示，则下列结论：①4a﹣b=0；②c＜0；③﹣3a+c＞0；④4a﹣2b＞at2+bt（t 为实数）；⑤点（﹣，y1），（﹣，y2），（﹣，y3）是该抛物线上的点，则y1＜y2＜y3，正确的个数有（）A. 4个B. 3个C. 2个D. 1个12.一次函数y=ax+b（a≠0）与二次函数y=ax2+bx+c（a≠0）在同一平面直角坐标系中的图象可能是（）A. B. C. D.13.二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C （，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（）A. 2个B. 3个C. 4个D. 5个14.如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1和3，则下列结论正确的是（）A. 2a﹣b=0B. a+b+c＞0C. 3a﹣c=0D. 当a= 时，△ABD是等腰直角三角形象如图所示，下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③3a+c＞0④当y＞0时，x的取值范围是﹣1≤x＜3⑤当x＜0时，y随x增大而增大其中结论正确的个数是（）A. 4个B. 3个C. 2个D. 1个二、填空题（共1题；共1分）16.如图，抛物线y=ax2+bx+c过点（﹣1，0），且对称轴为直线x=1，有下列结论：①abc＜0；②10a+3b+c＞0；③抛物线经过点（4，y1）与点（﹣3，y2），则y1＞y2；④无论a，b，c取何值，抛物线都经过同一个点（﹣，0）；⑤am2+bm+a≥0，其中所有正确的结论是________．答案部分一、单选题1.B2.C3.C4.B5.C6.A7.D8.B9.C 10.D 11.B 12.C 13.B 14.D 15.B二、填空题16.②④⑤。

2024年中考数学真题汇编专题14 二次函数的图象与性质+答案详解（试题部分）一、单选题1．（2024·内蒙古包头·中考真题）将抛物线22y x x =+向下平移2个单位后，所得新抛物线的顶点式为（ ） A ．()213y x =+− B ．()=+−2y x 12C ．()213y x =−−D ．()212y x =−−2．（2024·广东广州·中考真题）函数21y ax bx c =++与2ky x=的图象如图所示，当（ ）时，1y ，2y 均随着x 的增大而减小．A ．1x <−B ．10x −<<C ．02x <<D ．1x >3．（2024·四川凉山·中考真题）抛物线()2213y x c =−+经过()()1235202y y y ⎛⎫− ⎪⎝⎭，，，，，三点，则123y y y ，，的大小关系正确的是（ ） A ．123y y y >>B ．231y y y >>C ．312y y y >>D ．132y y y >>4．（2024·四川达州·中考真题）抛物线2y x bx c =−++与x 轴交于两点，其中一个交点的横坐标大于1，另一个交点的横坐标小于1，则下列结论正确的是（ ） A ．1b c +>B ．2b =C ．240b c +<D ．0c <5．（2024·四川泸州·中考真题）已知二次函数()2231y ax a x a =+−+−（x 是自变量）的图象经过第一、二、四象限，则实数a 的取值范围为（ ） A ．918a ≤< B ．302a << C ．908a <<D ．312a ≤<6．（2024·陕西·中考真题）已知一个二次函数2y ax bx c =++的自变量x 与函数y 的几组对应值如下表，则下列关于这个二次函数的结论正确的是（ ） A ．图象的开口向上B ．当0x >时，y 的值随x 的值增大而增大C ．图象经过第二、三、四象限D ．图象的对称轴是直线1x =7．（2024·湖北·中考真题）抛物线2y ax bx c =++的顶点为()1,2−−，抛物线与y 轴的交点位于x 轴上方．以下结论正确的是（ ） A ．0a <B ．0c <C ．2a b c −+=−D ．240b ac −=8．（2024·广东·中考真题）若点()()()1230,,1,,2,y y y 都在二次函数2y x =的图象上，则（ ） A ．321y y y >>B ．213y y y >>C ．132y y y >>D ．312y y y >>9．（2024·四川自贡·中考真题）一次函数24y x n =−+，二次函数2(1)3y x n x =+−−，反比例函数1n y x+=在同一直角坐标系中图象如图所示，则n 的取值范围是（ ）A ．1n >−B ．2n >C ．11n −<<D ．12n <<10．（2024·四川遂宁·中考真题）如图，已知抛物线2y ax bx c =++（a 、b 、c 为常数，且0a ≠）的对称轴为直线=1x −，且该抛物线与x 轴交于点()1,0A ，与y 轴的交点B 在()0,2−，()0,3−之间（不含端点），则下列结论正确的有多少个（ ）①0abc >； ②930a b c −+≥；③213a <<； ④若方程21ax bx c x +=++两根为(),m n m n <，则31m n −<<<．A ．1B ．2C ．3D ．411．（2024·江苏连云港·中考真题）已知抛物线2y ax bx c =++（a 、b 、c 是常数，a<0）的顶点为(1,2)．小烨同学得出以下结论：①0abc <；②当1x >时，y 随x 的增大而减小；③若20ax bx c ++=的一个根为3，则12a =−；④抛物线22y ax =+是由抛物线2y ax bx c =++向左平移1个单位，再向下平移2个单位得到的．其中一定正确的是（ ）A ．①②B ．②③C ．③④D ．②④12．（2024·四川广安·中考真题）如图，二次函数2y ax bx c =++（a ，b ，c 为常数，0a ≠）的图象与x 轴交于点3,02A ⎛⎫− ⎪⎝⎭，对称轴是直线12x =−，有以下结论：①0abc <；②若点()11,y −和点()22,y 都在抛物线上，则12y y <；③21142am bm a b +≤−（m 为任意实数）；④340a c +=．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个13．（2024·四川眉山·中考真题）如图，二次函数()20y ax bx c a =++≠的图象与x 轴交于点()3,0A ，与y 轴交于点B ，对称轴为直线1x =，下列四个结论：①0bc <；②320a c +<；③2ax bx a b +≥+；④若21c −<<−，则8433a b c −<++<−，其中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．414．（2024·福建·中考真题）已知二次函数()220y x ax a a =−+≠的图象经过1,2a A y ⎛⎫ ⎪⎝⎭，()23,B a y 两点，则下列判断正确的是（ ）A ．可以找到一个实数a ，使得1y a >B ．无论实数a 取什么值，都有1y a >C ．可以找到一个实数a ，使得20y <D ．无论实数a 取什么值，都有20y <15．（2024·贵州·中考真题）如图，二次函数2y ax bx c =++的部分图象与x 轴的一个交点的横坐标是3−，顶点坐标为()1,4−，则下列说法正确的是（ ）A ．二次函数图象的对称轴是直线1x =B ．二次函数图象与x 轴的另一个交点的横坐标是2C ．当1x <−时，y 随x 的增大而减小D ．二次函数图象与y 轴的交点的纵坐标是316．（2024·四川乐山·中考真题）已知二次函数()2211y x x x t =−−≤≤−，当=1x −时，函数取得最大值；当1x =时，函数取得最小值，则t 的取值范围是（ ）A ．02t <≤B ．04t <≤C ．24t ≤≤D ．2t ≥17．（2024·黑龙江绥化·中考真题）二次函数()20y ax bx c a =++≠的部分图象如图所示，对称轴为直线=1x −，则下列结论中： ①0bc> ②2am bm a b +≤−（m 为任意实数） ③31a c +< ④若()1,M x y 、()2,N x y 是抛物线上不同的两个点，则123x x +≤−．其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个18．（2024·四川广元·中考真题）如图，已知抛物线2y ax bx c =++过点()0,2C −与x 轴交点的横坐标分别为1x ，2x ，且110x −<<，223x <<，则下列结论：①<0a b c −+；②方程220ax bx c +++=有两个不相等的实数根； ③0a b +>； ④23a >； ⑤2244b ac a −>．其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个19．（2024·黑龙江牡丹江·中考真题）在平面直角坐标系中，抛物线()20y ax bx c a =++≠与x 轴交于A 、B两点，()()3,0,1,0A B −，与y 轴交点C 的纵坐标在3−～2−之间，根据图象判断以下结论：①20abc >；②423b <<；③若221122ax bx ax bx −=−且12x x ≠，则122x x +=−；④直线56y cx c =−+与抛物线2y ax bx c =++的一个交点(,)(0)m n m ≠，则12m =．其中正确的结论是（ ）A ．①②④B ．①③④C ．①②③D ．①②③④20．（2024·内蒙古赤峰·中考真题）如图，正方形ABCD 的顶点A ，C 在抛物线24y x =−+上，点D 在y 轴上．若A C ，两点的横坐标分别为m n ，（0m n >>），下列结论正确的是（ ）A ．1m n +=B ．1m n −=C ．1mn =D ．1m n= 21．（2024·四川宜宾·中考真题）如图，抛物线()20y ax bx c a =++<的图象交x 轴于点()3,0A −、()1,0B ，交y 轴于点C ．以下结论：①0a b c ++=；②320a b c ++<；③当以点A 、B 、C 为顶点的三角形是等腰三角形时，c =3c =时，在AOC 内有一动点P ，若2OP =，则23CP AP +．其中正确结论有（ ）A ．1个B ．2个C ．3个D ．4个22．（2024·黑龙江齐齐哈尔·中考真题）如图，二次函数()220y ax bx a =++≠的图象与x 轴交于()1,0−，1(,0)x ，其中123x <<．结合图象给出下列结论：①0ab >；②2a b −=−；③当1x >时，y 随x 的增大而减小；④关于x 的一元二次方程()2200ax bx a ++=≠的另一个根是2a−；⑤b 的取值范围为413b <<．其中正确结论的个数是（ ） A ．2B ．3C ．4D ．5二、填空题23．（2024·四川内江·中考真题）已知二次函数221y x x =−+的图象向左平移两个单位得到抛物线C ，点()12,P y ，()23,Q y 在抛物线C 上，则1y 2y （填“＞”或“＜”）；24．（2024·吉林长春·中考真题）若抛物线2y x x c =−+（c 是常数）与x 轴没有交点，则c 的取值范围是 ．25．（2024·黑龙江牡丹江·中考真题）将抛物线23y ax bx =++向下平移5个单位长度后，经过点()24,−，则637a b −−= ．26．（2024·四川成都·中考真题）在平面直角坐标系xOy 中，()11,A x y ，()22,B x y ，()33,C x y 是二次函数241y x x =−+−图象上三点．若101x <<，24x >，则1y 2y （填“>”或“<”）；若对于11m x m <<+，212m x m +<<+，323m x m +<<+，存在132y y y <<，则m 的取值范围是 ．27．（2024·上海·中考真题）对于一个二次函数2()y a x m k =−+（0a ≠）中存在一点(),P x y ''，使得0x m y k '−='−≠，则称2x m '−为该抛物线的“开口大小”，那么抛物线211323y x x =−++“开口大小”为 ．28．（2024·湖北武汉·中考真题）抛物线2y ax bx c =++（a ，b ，c 是常数，0a <）经过()1,1−，(),1m 两点，且01m <<．下列四个结论： ①0b >；②若01x <<，则()()2111a x b x c −+−+>；③若1a =−，则关于x 的一元二次方程 22ax bx c ++=无实数解；④点()11,A x y ，()22,B x y 在抛物线上，若1212x x +>−，12x x >，总有12y y <，则102m <≤．其中正确的是 （填写序号）．29．（2024·四川德阳·中考真题）如图，抛物线2y ax bx c =++的顶点A 的坐标为1,3n ⎛⎫− ⎪⎝⎭，与x 轴的一个交点位于0和1之间，则以下结论：①0abc >；②520b c +<；③若抛物线经过点()()126,,5,y y −，则12y y >；④若关于x 的一元二次方程24ax bx c ++=无实数根，则4n <．其中正确结论是 （请填写序号）．30．（2024·山东烟台·中考真题）已知二次函数2y ax bx c =++的y 与x 的部分对应值如下表：下列结论：①0abc >；②关于x 的一元二次方程29ax bx c ++=有两个相等的实数根；③当41x −<<时，y 的取值范围为<<0y 5；④若点()1,m y ，()22,m y −−均在二次函数图象上，则12y y =；⑤满足()212ax b x c +++<的x 的取值范围是<2x −或3x >．其中正确结论的序号为 ．三、解答题31．（2024·江苏扬州·中考真题）如图，已知二次函数2y x bx c =−++的图像与x 轴交于(2,0)A −，(1,0)B 两点．(1)求b c 、的值；(2)若点P 在该二次函数的图像上，且PAB 的面积为6，求点P 的坐标．32．（2024·安徽·中考真题）已知抛物线2y x bx =−+（b 为常数）的顶点横坐标比抛物线22y x x =−+的顶点横坐标大1． (1)求b 的值；(2)点()11,A x y 在抛物线22y x x =−+上，点()11,B x t y h ++在抛物线2y x bx =−+上． （ⅰ）若3h t =，且10x ≥，0t >，求h 的值； （ⅱ）若11x t =−，求h 的最大值．33．（2024·北京·中考真题）在平面直角坐标系xOy 中，已知抛物线()2220=−≠y ax a x a .(1)当1a =时，求抛物线的顶点坐标；(2)已知()11,M x y 和()22,N x y 是抛物线上的两点.若对于13x a =，234x ≤≤，都有12y y <，求a 的取值范围. 34．（2024·浙江·中考真题）已知二次函数2y x bx c =++（b ，c 为常数）的图象经过点(2,5)A −，对称轴为直线12x =−．(1)求二次函数的表达式；(2)若点(1,7)B 向上平移2个单位长度，向左平移m （0m >）个单位长度后，恰好落在2y x bx c =++的图象上，求m 的值；(3)当2x n −≤≤时，二次函数2y x bx c =++的最大值与最小值的差为94，求n 的取值范围．35．（2024·广西·中考真题）课堂上，数学老师组织同学们围绕关于x 的二次函数223y x ax a =++−的最值问题展开探究．【经典回顾】二次函数求最值的方法．（1）老师给出4a =−，求二次函数223y x ax a =++−的最小值． ①请你写出对应的函数解析式；②求当x 取何值时，函数y y 值；【举一反三】老师给出更多a 的值，同学们即求出对应的函数在x 取何值时，y 的最小值．记录结果，并整理成下表：注：*为②的计算结果．【探究发现】老师：“请同学们结合学过的函数知识，观察表格，谈谈你的发现．” 甲同学：“我发现，老师给了a 值后，我们只要取x a =−，就能得到y 的最小值．”乙同学：“我发现，y 的最小值随a 值的变化而变化，当a 由小变大时，y 的最小值先增大后减小，所以我猜想y 的最小值中存在最大值．”（2）请结合函数解析式223y x ax a =++−，解释甲同学的说法是否合理？（3）你认为乙同学的猜想是否正确？若正确，请求出此最大值；若不正确，说明理由．36．（2024·云南·中考真题）已知抛物线21y x bx =+−的对称轴是直线32x =．设m 是抛物线21y x bx =+−与x 轴交点的横坐标，记533109m M −=．(1)求b 的值；(2)比较M 37．（2024·四川成都·中考真题）如图，在平面直角坐标系xOy 中，抛物线L ：()2230y ax ax a a =−−>与x轴交于A ，B 两点（点A 在点B 的左侧），其顶点为C ，D 是抛物线第四象限上一点．(1)求线段AB 的长；(2)当1a =时，若ACD 的面积与ABD △的面积相等，求tan ABD ∠的值；(3)延长CD 交x 轴于点E ，当AD DE =时，将ADB 沿DE 方向平移得到A EB ''．将抛物线L 平移得到抛物线L '，使得点A '，B '都落在抛物线L '上．试判断抛物线L '与L 是否交于某个定点．若是，求出该定点坐标；若不是，请说明理由．38．（2024·山东·中考真题）在平面直角坐标系xOy 中，点()2,3P −在二次函数()230y ax bx a =+−>的图像上，记该二次函数图像的对称轴为直线x m =． (1)求m 的值；(2)若点(),4Q m −在23y ax bx =+−的图像上，将该二次函数的图像向上平移5个单位长度，得到新的二次函数的图像．当04x ≤≤时，求新的二次函数的最大值与最小值的和；(3)设23y ax bx =+−的图像与x 轴交点为()1,0x ，()()212,0x x x <．若2146x x <−<，求a 的取值范围． 39．（2024·四川乐山·中考真题）在平面直角坐标系xOy 中，我们称横坐标、纵坐标都为整数的点为“完美点”．抛物线222y ax ax a =−+（a 为常数且0a >）与y 轴交于点A ．(1)若1a=，求抛物线的顶点坐标；(2)若线段OA（含端点）上的“完美点”个数大于3个且小于6个，求a的取值范围；=交于M、N两点，线段MN与抛物线围成的区域（含边界）内恰有4个“完美点”，(3)若抛物线与直线y x求a的取值范围．2024年中考数学真题汇编专题14 二次函数的图象与性质+答案详解（答案详解）一、单选题1．（2024·内蒙古包头·中考真题）将抛物线22y x x =+向下平移2个单位后，所得新抛物线的顶点式为（ ） A ．()213y x =+− B ．()=+−2y x 12C ．()213y x =−−D ．()212y x =−− 【答案】A【分析】本题主要考查了二次函数的平移以及顶点式，根据平移的规律“上加下减．左加右减”可得出平移后的抛物线为222y x x =+−，再把222y x x =+−化为顶点式即可．【详解】解：抛物线22y x x =+向下平移2个单位后，则抛物线变为222y x x =+−，∴222y x x =+−化成顶点式则为 ()213y x =+−，故选：A ．2．（2024·广东广州·中考真题）函数21y ax bx c =++与2k y x=的图象如图所示，当（ ）时，1y ，2y 均随着x 的增大而减小．A ．1x <−B ．10x −<<C ．02x <<D ．1x >【答案】D 【分析】本题考查了二次函数以及反比例函数的图象和性质，利用数形结合的思想解决问题是关键．由函数图象可知，当1x >时，1y 随着x 的增大而减小；2y 位于在一、三象限内，且2y 均随着x 的增大而减小，据此即可得到答案．【详解】解：由函数图象可知，当1x >时，1y 随着x 的增大而减小；2y 位于一、三象限内，且在每一象限内2y 均随着x 的增大而减小，∴当1x >时，1y ，2y 均随着x 的增大而减小，故选：D ．3．（2024·四川凉山·中考真题）抛物线()2213y x c =−+经过()()1235202y y y ⎛⎫− ⎪⎝⎭，，，，，三点，则123y y y ，，的大小关系正确的是（ ）A ．123y y y >>B ．231y y y >>C ．312y y y >>D ．132y y y >>4．（2024·四川达州·中考真题）抛物线2y x bx c =−++与x 轴交于两点，其中一个交点的横坐标大于1，另一个交点的横坐标小于1，则下列结论正确的是（ ）A ．1b c +>B ．2b =C ．240b c +<D ．0c <【答案】A【分析】本题考查了二次函数的性质，设抛物线2y x bx c =−++与x 轴交于两点，横坐标分别为1212,,x x x x <，依题意，121,1x x <>，根据题意抛物线开口向下，当1x =时，0y >，即可判断A 选项，根据对称轴即可判断B 选项，根据一元二次方程根的判别式，即可求解．判断C 选项，无条件判断D 选项，据此，即可求解．【详解】解：依题意，设抛物线2y x bx c =−++与x 轴交于两点，横坐标分别为1212,,x x x x <依题意，121,1x x <>∵10a =−<，抛物线开口向下，∴当1x =时，0y >，即10b c −++>5．（2024·四川泸州·中考真题）已知二次函数()2231y ax a x a =+−+−（x 是自变量）的图象经过第一、二、四象限，则实数a 的取值范围为（ ）A ．918a ≤<B ．302a <<C ．908a <<D ．312a ≤< 【详解】解：二次函数6．（2024·陕西·中考真题）已知一个二次函数2y ax bx c =++的自变量x 与函数y 的几组对应值如下表，则下列关于这个二次函数的结论正确的是（ ）A ．图象的开口向上B ．当0x >时，y 的值随x 的值增大而增大C ．图象经过第二、三、四象限D ．图象的对称轴是直线1x =7．（2024·湖北·中考真题）抛物线2y ax bx c =++的顶点为1,2−−，抛物线与轴的交点位于x 轴上方．以下结论正确的是（ ）A ．0a <B ．0c <C ．2a b c −+=−D ．240b ac −= 【答案】C【分析】本题考查了二次函数的性质以及二次函数图像与系数的关系．根据二次函数的解析式结合二次函数的性质，画出草图，逐一分析即可得出结论．【详解】解：根据题意画出函数2y ax bx c =++的图像，如图所示：∵开口向上，与y 轴的交点位于x 轴上方，∴0a >，0c >，∵抛物线与x 轴有两个交点，∴240b ac ∆=−>，∵抛物线2y ax bx c =++的顶点为()1,2−−，∴2a b c −+=−，观察四个选项，选项C 符合题意，故选：C ．8．（2024·广东·中考真题）若点()()()1230,,1,,2,y y y 都在二次函数2y x =的图象上，则（ ）A ．321y y y >>B ．213y y y >>C ．132y y y >>D ．312y y y >> 【答案】A【分析】本题考查了二次函数的图象和性质、二次函数图象上点的坐标特征等知识点，根据二次函数的解析式得出函数图象的对称轴是y 轴（直线0x =），图象的开口向上，在对称轴的右侧，y 随x 的增大而增大，再比较即可．【详解】解∶ 二次函数2y x =的对称轴为y 轴，开口向上， ∴当0x >时， y 随x 的增大而增大，∵点()()()1230,,1,,2,y y y 都在二次函数2y x =的图象上，且012<<， ∴321y y y >>，故选∶A ．9．（2024·四川自贡·中考真题）一次函数24y x n =−+，二次函数2(1)3y x n x =+−−，反比例函数1n y x+=在同一直角坐标系中图象如图所示，则n 的取值范围是（ ）A ．1n >−B ．2n >C ．11n −<<D ．12n <<【答案】C10．（2024·四川遂宁·中考真题）如图，已知抛物线2y ax bx c =++（a 、b 、c 为常数，且0a ≠）的对称轴为直线=1x −，且该抛物线与x 轴交于点()1,0A ，与y 轴的交点B 在()0,2−，()0,3−之间（不含端点），则下列结论正确的有多少个（ ）①0abc >；②930a b c −+≥；③213a <<； ④若方程21ax bx c x +=++两根为(),m n m n <，则31m n −<<<．A ．1B ．2C ．3D ．4 【答案】B【分析】本题主要考查二次函数和一次函数的性质，根据题干可得0a >，20b a =>，32c −<<−，即可判断①错误；根据对称轴和一个交点求得另一个交点为()3,0−，即可判断②错误；将c 和b 用a 表示，即可得到332a −<−<−，即可判断③正确；结合抛物线2y ax bx c =++和直线1y x =+与x 轴得交点，即可判断④正确．【详解】解：由图可知0a >，11．（2024·江苏连云港·中考真题）已知抛物线2y ax bx c =++（a 、b 、c 是常数，a<0）的顶点为(1,2)．小烨同学得出以下结论：①0abc <；②当1x >时，y 随x 的增大而减小；③若20ax bx c ++=的一个根为3，则12a =−；④抛物线22y ax =+是由抛物线2y ax bx c =++向左平移1个单位，再向下平移2个单位得到的．其中一定正确的是（ ）A ．①②B ．②③C ．③④D ．②④【答案】B0a <，02b ∴−<即a bc ++2c a ∴=−c ∴的值可正也可负，a<2,b a =−∴抛物线为09a =−12a ∴=−，故③正确；抛物线12．（2024·四川广安·中考真题）如图，二次函数2y ax bx c =++（a ，b ，c 为常数，0a ≠）的图象与x 轴交于点3,02A ⎛⎫− ⎪⎝⎭，对称轴是直线12x =−，有以下结论：①0abc <；②若点()11,y −和点()22,y 都在抛物线上，则12y y <；③21142am bm a b +≤−（m 为任意实数）；④340a c +=．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个 <02b a−，<0b ∴.>0abc ∴.故①错误；对称轴是直线而(1−−−−故选：B.【点睛】本题考查了二次函数图像与系数之间的关系，解题的关键在于通过图像判断对称轴，开口方向以及与坐标轴的交点.13．（2024·四川眉山·中考真题）如图，二次函数()20y ax bx c a =++≠的图象与x 轴交于点()3,0A ，与y 轴交于点B ，对称轴为直线1x =，下列四个结论：①0bc <；②320a c +<；③2ax bx a b +≥+；④若21c −<<−，则8433a b c −<++<−，其中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4【详解】解：①函数图象开口方向向上，对称轴在②二次函数2b a =−，1x ∴=−时，a b c ∴−+3a c ∴+=③对称轴为直线④2c −<<∴根据抛物线与相应方程的根与系数的关系可得3c a =−，23a ∴−<−<−1233a <<，2b a =−，a bc ∴++83a ∴−<+故④正确；综上所述，正确的有②③④，14．（2024·福建·中考真题）已知二次函数()220y x ax a a =−+≠的图象经过1,2a A y ⎛⎫ ⎪⎝⎭，()23,B a y 两点，则下列判断正确的是（ ）A ．可以找到一个实数a ，使得1y a >B ．无论实数a 取什么值，都有1y a >C ．可以找到一个实数a ，使得20y <D ．无论实数a 取什么值，都有20y <【详解】解：二次函数解析式为当15．（2024·贵州·中考真题）如图，二次函数2y ax bx c =++的部分图象与x 轴的一个交点的横坐标是3−，顶点坐标为()1,4−，则下列说法正确的是（ ）A ．二次函数图象的对称轴是直线1x =B ．二次函数图象与x 轴的另一个交点的横坐标是2C ．当1x <−时，y 随x 的增大而减小D ．二次函数图象与y 轴的交点的纵坐标是3 【答案】D【分析】本题考查了二次函数的性质，待定系数法求二次函数解析式，利用二次函数的性质，对称性，增减性判断选项A 、B 、C ，利用待定系数法求出二次函数的解析式，再求出与y 轴的交点坐标即可判定选项D ．【详解】解∶ ∵二次函数2y ax bx c =++的顶点坐标为()1,4−， ∴二次函数图象的对称轴是直线=1x −，故选项A 错误；∵二次函数2y ax bx c =++的图象与x 轴的一个交点的横坐标是3−，对称轴是直线=1x −， ∴二次函数图象与x 轴的另一个交点的横坐标是1，故选项B 错误； ∵抛物线开口向下， 对称轴是直线=1x −，∴当1x <−时，y 随x 的增大而增大，故选项C 错误； 设二次函数解析式为()214y a x =++， 把()3,0−代入，得()20314a =−++，解得1a =−， ∴()214y x =−++，当0x =时，()20143y =−++=，∴二次函数图象与y 轴的交点的纵坐标是3，故选项D 正确， 故选D ．16．（2024·四川乐山·中考真题）已知二次函数()2211y x x x t =−−≤≤−，当=1x −时，函数取得最大值；当1x =时，函数取得最小值，则t 的取值范围是（ ）A ．02t <≤B ．04t <≤C ．24t ≤≤D ．2t ≥【答案】C【分析】本题考查了二次函数的图象与性质，二次函数的最值等知识．熟练掌握二次函数的图象与性质是解题的关键．由()22211y x x x =−=−−，可知图象开口向上，对称轴为直线1x =，顶点坐标为()11−，，当=1x −时，3y =，即()13−，关于对称轴对称的点坐标为()33，，由当=1x −时，函数取得最大值；当1x =时，函数取得最小值，可得113t ≤−≤，计算求解，然后作答即可． 【详解】解：∵()22211y x x x =−=−−，∴图象开口向上，对称轴为直线1x =，顶点坐标为()11−，， 当=1x −时，3y =，∴()13−，关于对称轴对称的点坐标为()33，， ∵当=1x −时，函数取得最大值；当1x =时，函数取得最小值， ∴113t ≤−≤， 解得，24t ≤≤，故选：C ．17．（2024·黑龙江绥化·中考真题）二次函数()20y ax bx c a =++≠的部分图象如图所示，对称轴为直线=1x −，则下列结论中： ①0bc> ②2am bm a b +≤−（m 为任意实数） ③31a c +< ④若()1,M x y 、()2,N x y 是抛物线上不同的两个点，则123x x +≤−．其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个18．（2024·四川广元·中考真题）如图，已知抛物线2y ax bx c =++过点()0,2C −与x 轴交点的横坐标分别为1x ，2x ，且110x −<<，223x <<，则下列结论：①<0a b c −+；②方程220ax bx c +++=有两个不相等的实数根； ③0a b +>； ④23a >； ⑤2244b ac a −>．其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【详解】解：①抛物线开口向上，∴2244b ac a −>，故⑤符合题意； 故选：C ．19．（2024·黑龙江牡丹江·中考真题）在平面直角坐标系中，抛物线()20y ax bx c a =++≠与x 轴交于A 、B两点，()()3,0,1,0A B −，与y 轴交点C 的纵坐标在3−～2−之间，根据图象判断以下结论：①20abc >；②423b <<；③若221122ax bx ax bx −=−且12x x ≠，则122x x +=−；④直线56y cx c =−+与抛物线2y ax bx c =++的一个交点(,)(0)m n m ≠，则12m =．其中正确的结论是（ ）A ．①②④B ．①③④C ．①②③D ．①②③④20．（2024·内蒙古赤峰·中考真题）如图，正方形ABCD 的顶点A ，C 在抛物线24y x =−+上，点D 在y 轴上．若A C ，两点的横坐标分别为m n ，（0m n >>），下列结论正确的是（ ）A ．1m n +=B ．1m n −=C ．1mn =D ．1mn= 先证明(AAS)ANB DMA ≌2)4n +．(2m n E +，4b +−，AM m =，四边形AC ∴、BD 互相平分，AB =90BAN DAM ∴∠+∠=︒，DAM ∠BAN ADM ∴∠=∠．90BNA AMD ∠=∠=︒，BA (AAS)ANB DMA ∴≌．AM NB ∴=，DMAN =．点A 、C 的横坐标分别为24(,)A m m ∴+−，(C (m n E +∴，2m n −−点21．（2024·四川宜宾·中考真题）如图，抛物线()20y ax bx c a =++<的图象交x 轴于点()3,0A −、()1,0B ，交y 轴于点C ．以下结论：①0a b c ++=；②320a b c ++<；③当以点A 、B 、C 为顶点的三角形是等腰三角形时，c =3c =时，在AOC 内有一动点P ，若2OP =，则23CP AP +．其中正确结论有（ ）A．1个B．2个C．3个D．4个3⎝⎭∴42323 OHOP==，∵23 OPOA=，∴OH OP OP OA=，又∵HOP POA∠=∠，Rt OCH 中，由勾股定理得∴正确的有3个，故选：C ．【点睛】本题主要考查了二次函数图象的性质，熟练掌握二次函数的相关知识是解题的关键．22．（2024·黑龙江齐齐哈尔·中考真题）如图，二次函数()220y ax bx a =++≠的图象与x 轴交于()1,0−，1(,0)x ，其中123x <<．结合图象给出下列结论：①0ab >；②2a b −=−；③当1x >时，y 随x 的增大而减小；④关于x 的一元二次方程()2200ax bx a ++=≠的另一个根是2a−；⑤b 的取值范围为413b <<．其中正确结论的个数是（ ） A ．2 B ．3 C ．4 D ．5该函数图象与该图象中，当2b a =+∴关于x 的一元二次方程b x −±=0a <，(1a x −∴=∴④正确；123x <<解得1−<a b −=−1b ∴−<−413b ∴<<∴⑤正确．综上，②③④⑤正确，共二、填空题23．（2024·四川内江·中考真题）已知二次函数221y x x =−+的图象向左平移两个单位得到抛物线C ，点()12,P y ，()23,Q y 在抛物线C 上，则1y 2y （填“＞”或“＜”）； 【答案】<【分析】本题主要考查了二次函数图象的平移以及二次函数的性质，由平移的规律可得出抛物线C 的解析式为()21y x =+，再利用二次函数图象的性质可得出答案． 【详解】解：()22211y x x x =−+=−，∵二次函数221y x x =−+的图象向左平移两个单位得到抛物线C ， ∴抛物线C 的解析式为()21y x =+， ∴抛物线开口向上，对称轴为=1x −， ∴当1x >−时，y 随x 的增大而增大， ∵23<， ∴12y y <， 故答案为：<．24．（2024·吉林长春·中考真题）若抛物线2y x x c =−+（c 是常数）与x 轴没有交点，则c 的取值范围是 ．25．（2024·黑龙江牡丹江·中考真题）将抛物线23y ax bx =++向下平移5个单位长度后，经过点()24,−，则637a b −−= ． 【答案】2【分析】此题考查了二次函数的平移，根据平移规律得到函数解析式，把点的坐标代入得到23a b −=，再整体代入变形后代数式即可．【详解】解：抛物线23y ax bx =++向下平移5个单位长度后得到22352y ax bx ax bx =++−=+−， 把点()24,−代入得到，()24222a b =⨯−−−，得到23a b −=，∴()6373273372a b a b −−=−−=⨯−=， 故答案为：226．（2024·四川成都·中考真题）在平面直角坐标系xOy 中，()11,A x y ，()22,B x y ，()33,C x y 是二次函数241y x x =−+−图象上三点．若101x <<，24x >，则1y 2y （填“>”或“<”）；若对于11m x m <<+，212m x m +<<+，323m x m +<<+，存在132y y y <<，则m 的取值范围是 ．27．（2024·上海·中考真题）对于一个二次函数2()y a x m k =−+（0a ≠）中存在一点(),P x y ''，使得0x m y k '−='−≠，则称2x m '−为该抛物线的“开口大小”，那么抛物线211323y x x =−++“开口大小”为 ．y 28．（2024·湖北武汉·中考真题）抛物线2y ax bx c =++（a ，b ，c 是常数，0a <）经过()1,1−，(),1m 两点，且01m <<．下列四个结论： ①0b >；②若01x <<，则()()2111a x b x c −+−+>；③若1a =−，则关于x 的一元二次方程 22ax bx c ++=无实数解；④点()11,A x y ，()22,B x y 在抛物线上，若1212x x +>−，12x x >，总有12y y <，则102m <≤．其中正确的是 （填写序号）．29．（2024·四川德阳·中考真题）如图，抛物线2y ax bx c =++的顶点A 的坐标为1,3n ⎛⎫− ⎪⎝⎭，与x 轴的一个交点位于0和1之间，则以下结论：①0abc >；②520b c +<；③若抛物线经过点()()126,,5,y y −，则12y y >；④若关于x 的一元二次方程24ax bx c ++=无实数根，则4n <．其中正确结论是 （请填写序号）．30．（2024·山东烟台·中考真题）已知二次函数2y ax bx c =++的y 与x 的部分对应值如下表：下列结论：①0abc >；②关于x 的一元二次方程29ax bx c ++=有两个相等的实数根；③当41x −<<时，y 的取值范围为<<0y 5；④若点()1,m y ，()22,m y −−均在二次函数图象上，则12y y =；⑤满足()212ax b x c +++<的x 的取值范围是<2x −或3x >．其中正确结论的序号为 ．【答案】①②④由2228y x y x x =−+⎧⎨=−−+⎩，解得1120x y =⎧⎨=⎩，2235x y =−⎧⎨=⎩， ∴()2,0A ，()3,5B −，由图形可得，当3x <−或2x >时，2282x x x −−+<−+，即()212ax b x c +++<，故⑤错误；综上，正确的结论为①②④， 故答案为：①②④．三、解答题31．（2024·江苏扬州·中考真题）如图，已知二次函数2y x bx c =−++的图像与x 轴交于(2,0)A −，(1,0)B 两点．(1)求b c 、的值；(2)若点P 在该二次函数的图像上，且PAB 的面积为6，求点P 的坐标． 【答案】(1)12b c =−=，(2)122434()()P P −−−，，，【分析】本题主要考查二次函数与几何图形的综合，掌握待定系数法求解析式，解一元二次方程的方法是1PABS=4n =，4n =±，32．（2024·安徽·中考真题）已知抛物线2y x bx =−+（b 为常数）的顶点横坐标比抛物线22y x x =−+的顶点横坐标大1． (1)求b 的值；(2)点()11,A x y 在抛物线22y x x =−+上，点()11,B x t y h ++在抛物线2y x bx =−+上． （ⅰ）若3h t =，且10x ≥，0t >，求h 的值； （ⅱ）若11x t =−，求h 的最大值． 【答案】(1)4b =33．（2024·北京·中考真题）在平面直角坐标系xOy 中，已知抛物线()2220=−≠y ax a x a .(1)当1a =时，求抛物线的顶点坐标；(2)已知()11,M x y 和()22,N x y 是抛物线上的两点.若对于13x a =，234x ≤≤，都有12y y <，求a 的取值范围.综上，当01a <<或4a <−，都有12y y <．34．（2024·浙江·中考真题）已知二次函数2y x bx c =++（b ，c 为常数）的图象经过点(2,5)A −，对称轴为直线12x =−．(1)求二次函数的表达式；(2)若点(1,7)B 向上平移2个单位长度，向左平移m （0m >）个单位长度后，恰好落在2y x bx c =++的图象上，求m 的值；(3)当2x n −≤≤时，二次函数2y x bx c =++的最大值与最小值的差为94，求n 的取值范围．35．（2024·广西·中考真题）课堂上，数学老师组织同学们围绕关于x 的二次函数223y x ax a =++−的最值问题展开探究．【经典回顾】二次函数求最值的方法．（1）老师给出4a =−，求二次函数223y x ax a =++−的最小值． ①请你写出对应的函数解析式；②求当x 取何值时，函数y 有最小值，并写出此时的y 值；【举一反三】老师给出更多a 的值，同学们即求出对应的函数在x 取何值时，y 的最小值．记录结果，并整理成下表：注：*为②的计算结果．【探究发现】老师：“请同学们结合学过的函数知识，观察表格，谈谈你的发现．” 甲同学：“我发现，老师给了a 值后，我们只要取x a =−，就能得到y 的最小值．”乙同学：“我发现，y 的最小值随a 值的变化而变化，当a 由小变大时，y 的最小值先增大后减小，所以我猜想y 的最小值中存在最大值．”（2）请结合函数解析式223y x ax a =++−，解释甲同学的说法是否合理？（3）你认为乙同学的猜想是否正确？若正确，请求出此最大值；若不正确，说明理由．36．（2024·云南·中考真题）已知抛物线21y x bx =+−的对称轴是直线32x =．设m 是抛物线21y x bx =+−与x 轴交点的横坐标，记533109m M −=．(1)求b 的值；(2)比较M。

专题 二次函数图象及其性质二次函数的图象与系数的关系一、考点扫描二次函数)0(2≠++=a c bx ax y 的图象与系数的关系如下：1、a 决定抛物线的开口方向：当a ＞0时，抛物线开口向上；当a ＜0时，抛物线开口向下。

2、a 决定抛物线的开口大小：a 越大，则开口越小；a 越小，则开口越大。

3、a 、b 的符号决定抛物线的对称轴：当a 、b 同号时，对称轴在y 轴的左侧；当a 、b 异号时，对称轴在y 轴的右侧。

特别地，若抛物线的对称轴是直线x ＝1，则ab2-＝1，即b ＝－2a ；若抛物线的对称轴是直线x ＝－1，则ab2-＝－1，即b ＝2a ． 4、c 是抛物线与y 轴交点的纵坐标：当0=c 时，抛物线经过原点；当c ＞0时，抛物线与y 轴交于正半轴；当c ＜0时，抛物线与y 轴交于负半轴。

5、ac b 42-决定图象与x 轴是否相交：当ac b 42-＞0时，抛物线与x 轴有两个交点；当042=-ac b 时，抛物线与x 轴只有一个交点；当ac b 42-＜0时，抛物线与x 轴没有交点。

6、根据抛物线与x 轴的位置关系可以确定b 2－4ac 的符号．因为当y ＝0时ax 2＋bx ＋c ＝0，所以抛物线与x 轴有两个交点时，方程ax 2＋bx ＋c ＝0有两个不相等的实数根，此时b 2－4ac ＞0；抛物线与x 轴只有一个交点时，方程ax 2＋bx ＋c ＝0有两个相等的实数根，此时b 2－4ac ＝0；抛物线与x 轴没有交点时，方程ax 2＋bx ＋c ＝0没有实数根，此时b 2－4ac ＜0．7、根据直线x ＝1与抛物线交点的位置可以确定a ＋b ＋c 的符号。

交点在x 轴上，a ＋b ＋c ＝0；交点在第一象限a ＋b ＋c ＞0；交点在第四象限a ＋b ＋c ＜0．同样根据直线x ＝－1与抛物线交点的位置可以确定a －b ＋c 的符号（自己探索）．反过来，可以由系数a 、b 、c 的符号可确定抛物线y ＝ax 2＋bx ＋c 的大致形状．应用上述关系，便能简洁明快地根据a 、b 、c 的符号判断抛物线的位置，或者根据抛物线的位置确定a 、b 、c 的符号。

中考数学复习----《二次函数之定义、图像以及性质》知识点总与专项练习题（含答案解析）知识点总结1. 二次函数的定义：形如()02≠++=a c bx ax y 的函数叫做二次函数。

2. 二次函数的图像：二次函数的图像是一条抛物线。

3. 二次函数的性质与图像：x 的增大而增大； 的增大而减小； 的增大而增大； 的增大而减小；①若二次函数是一般形式时，则二次函数与y 轴的交点坐标为()c ，0。

若0＞c ，则二次函数与y 轴交于正半轴；若0＜c ，则二次函数与y 轴交于负半轴。

②二次函数开口向上时，离对称轴越远的点函数值越大；二次函数开口向下时，离对称轴越远的函数值越小。

③二次函数函数值相等的两个点一定关于对称轴对称。

④二次函数的一般式化为顶点式：利用一元二次方程的配方法。

专项练习题1．（2022•济南）某学校要建一块矩形菜地供学生参加劳动实践，菜地的一边靠墙，另外三边用木栏围成，木栏总长为40m ．如图所示，设矩形一边长为xm ，另一边长为ym ，当x 在一定范围内变化时，y 随x 的变化而变化，则y 与x 满足的函数关系是（ ）A ．正比例函数关系B ．一次函数关系C ．反比例函数关系D ．二次函数关系【分析】根据题意列出y 与x 的关系式可得答案． 【解答】解：由题意得，y ＝40﹣2x ， 所以y 与x 是一次函数关系， 故选：B ．2．（2022•株洲）已知二次函数y ＝ax 2+bx ﹣c （a ≠0），其中b ＞0、c ＞0，则该函数的图象可能为（ ）A ．B ．C．D．【分析】根据c＞0，可知﹣c＜0，可排除A，D选项，当a＞0时，可知对称轴＜0，可排除B选项，当a＜0时，可知对称轴＞0，可知C选项符合题意．【解答】解：∵c＞0，∴﹣c＜0，故A，D选项不符合题意；当a＞0时，∵b＞0，∴对称轴x＝＜0，故B选项不符合题意；当a＜0时，b＞0，∴对称轴x＝＞0，故C选项符合题意，故选：C．3．（2022•阜新）下列关于二次函数y＝3（x+1）（2﹣x）的图象和性质的叙述中，正确的是（）A．点（0，2）在函数图象上B．开口方向向上C．对称轴是直线x＝1D．与直线y＝3x有两个交点【分析】A、把x＝0代入y＝3（x+1）（2﹣x），求函数值再与点的纵坐标进行比较；B、化简二次函数：y＝﹣3x2+3x+6，根据a的取值判断开口方向；C、根据对称轴公式计算；D、把函数的问题转化为一元二次方程的问题，根据判别式的取值来判断．【解答】解：A、把x＝0代入y＝3（x+1）（2﹣x），得y＝6≠2，∴A错误；B 、化简二次函数：y ＝﹣3x 2+3x +6， ∵a ＝﹣3＜0，∴二次函数的图象开口方向向下， ∴B 错误；C 、∵二次函数对称轴是直线x ＝﹣＝， ∴C 错误；D 、∵3（x +1）（2﹣x ）＝3x ， ∴﹣3x 2+3x +6＝3x ， ∴﹣3x 2+6＝0， ∵b 2﹣4ac ＝72＞0，∴二次函数y ＝3（x +1）（2﹣x ）的图象与直线y ＝3x 有两个交点， ∴D 正确； 故选：D ．4．（2022•衢州）已知二次函数y ＝a （x ﹣1）2﹣a （a ≠0），当﹣1≤x ≤4时，y 的最小值为﹣4，则a 的值为（ ） A ．21或4 B ．34或﹣21 C ．﹣34或4 D ．﹣21或4 【分析】分两种情况讨论：当a ＞0时，﹣a ＝﹣4，解得a ＝4；当a ＜0时，在﹣1≤x ≤4，9a ﹣a ＝﹣4，解得a ＝﹣．【解答】解：y ＝a （x ﹣1）2﹣a 的对称轴为直线x ＝1， 顶点坐标为（1，﹣a ），当a ＞0时，在﹣1≤x ≤4，函数有最小值﹣a ， ∵y 的最小值为﹣4， ∴﹣a ＝﹣4， ∴a ＝4；当a ＜0时，在﹣1≤x ≤4，当x ＝4时，函数有最小值， ∴9a ﹣a ＝﹣4， 解得a ＝﹣；综上所述：a的值为4或﹣，故选：D．5．（2022•荆门）抛物线y＝x2+3上有两点A（x1，y1），B（x2，y2），若y1＜y2，则下列结论正确的是（）A．0≤x1＜x2B．x2＜x1≤0C．x2＜x1≤0或0≤x1＜x2D．以上都不对【分析】根据二次函数的性质判断即可．【解答】解：∵抛物线y＝x2+3上有两点A（x1，y1），B（x2，y2），且y1＜y2，∴|x1|＜|x2|，∴0≤x1＜x2或x2＜x1≤0或0＜﹣x1＜x2或0＜x1＜﹣x2，故选：D．6．（2022•兰州）已知二次函数y＝2x2﹣4x+5，当函数值y随x值的增大而增大时，x的取值范围是（）A．x＜1B．x＞1C．x＜2D．x＞2【分析】将二次函数解析式化为顶点式，由抛物线对称轴及开口方向求解．【解答】解：∵y＝2x2﹣4x+5＝2（x﹣1）2+3，∴抛物线开口向上，对称轴为直线x＝1，∴x＞1时，y随x增大而增大，故选：B．7．（2022•广州）如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为x＝﹣2，下列结论正确的是（）A．a＜0B．c＞0C．当x＜﹣2时，y随x的增大而减小D．当x＞﹣2时，y随x的增大而减小【分析】根据图象得出a，c的符号即可判断A、B，利用二次函数的性质即可判断C、D．【解答】解：∵图象开口向上，∴a＞0，故A不正确；∵图象与y轴交于负半轴，∴c＜0，故B不正确；∵抛物线开口向上，对称轴为直线x＝﹣2，∴当x＜﹣2时，y随x的增大而减小，x＞﹣2时，y随x的增大而增大，故C正确，D不正确；故选：C．8．（2022•郴州）关于二次函数y＝（x﹣1）2+5，下列说法正确的是（）A．函数图象的开口向下B．函数图象的顶点坐标是（﹣1，5）C．该函数有最大值，最大值是5D．当x＞1时，y随x的增大而增大【分析】通过分析二次函数顶点式判断函数图象开口方向、顶点坐标、最值以及增减性即可求解．【解答】解：y＝（x﹣1）2+5中，x2的系数为1，1＞0，函数图象开口向上，A错误；函数图象的顶点坐标是（1，5），B错误；函数图象开口向上，有最小值为5，C错误；函数图象的对称轴为x＝1，x＜1时y随x的增大而减小；x＞1时，y随x的增大而增大，D正确．故选：D．9．（2022•哈尔滨）抛物线y＝2（x+9）2﹣3的顶点坐标是（）A．（9，﹣3）B．（﹣9，﹣3）C．（9，3）D．（﹣9，3）【分析】由抛物线解析式可得抛物线顶点坐标．【解答】解：∵y＝2（x+9）2﹣3，∴抛物线顶点坐标为（﹣9，﹣3），故选：B．10．（2022•岳阳）已知二次函数y＝mx2﹣4m2x﹣3（m为常数，m≠0），点P（x p，y p）是该函数图象上一点，当0≤x p≤4时，y p≤﹣3，则m的取值范围是（）A．m≥1或m＜0B．m≥1C．m≤﹣1或m＞0D．m≤﹣1【分析】先求出抛物线的对称轴及抛物线与y轴的交点坐标，再分两种情况：m＞0或m ＜0，根据二次函数的性质求得m的不同取值范围便可．【解答】解：∵二次函数y＝mx2﹣4m2x﹣3，∴对称轴为x＝2m，抛物线与y轴的交点为（0，﹣3），∵点P（x p，y p）是该函数图象上一点，当0≤x p≤4时，y p≤﹣3，∴①当m＞0时，对称轴x＝2m＞0，此时，当x＝4时，y≤﹣3，即m•42﹣4m2•4﹣3≤﹣3，解得m≥1；②当m＜0时，对称轴x＝2m＜0，当0≤x≤4时，y随x增大而减小，则当0≤x p≤4时，y p≤﹣3恒成立；综上，m的取值范围是：m≥1或m＜0．故选：A．11．（2022•陕西）已知二次函数y＝x2﹣2x﹣3的自变量x1，x2，x3对应的函数值分别为y1，y2，y3．当﹣1＜x1＜0，1＜x2＜2，x3＞3时，y1，y2，y3三者之间的大小关系是（）A．y1＜y2＜y3B．y2＜y3＜y1C．y3＜y1＜y2D．y2＜y1＜y3【分析】首先求出抛物线的对称轴，根据二次函数的增减性即可解决问题．【解答】解：∵抛物线y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴对称轴x＝1，顶点坐标为（1，﹣4），当y＝0时，（x﹣1）2﹣4＝0，解得x＝﹣1或x＝3，∴抛物线与x轴的两个交点坐标为：（﹣1，0），（3，0），∴当﹣1＜x1＜0，1＜x2＜2，x3＞3时，y2＜y1＜y3，故选：D．12．（2022•新疆）已知抛物线y＝（x﹣2）2+1，下列结论错误的是（）A．抛物线开口向上B．抛物线的对称轴为直线x＝2C．抛物线的顶点坐标为（2，1）D．当x＜2时，y随x的增大而增大【分析】根据抛物线a＞0时，开口向上，a＜0时，开口向下判断A选项；根据抛物线的对称轴为x＝h判断B选项；根据抛物线的顶点坐标为（h，k）判断C选项；根据抛物线a＞0，x＜h时，y随x的增大而减小判断D选项．【解答】解：A选项，∵a＝1＞0，∴抛物线开口向上，故该选项不符合题意；B选项，抛物线的对称轴为直线x＝2，故该选项不符合题意；C选项，抛物线的顶点坐标为（2，1），故该选项不符合题意；D选项，当x＜2时，y随x的增大而减小，故该选项符合题意；故选：D．13．（2022•盐城）若点P（m，n）在二次函数y＝x2+2x+2的图象上，且点P到y轴的距离小于2，则n的取值范围是．【分析】由题意可知﹣2＜m＜2，根据m的范围即可确定n的范围．【解答】解：∵y＝x2+2x+2＝（x+1）2+1，∴二次函数y＝x2+2x+2的图象开口向上，顶点为（﹣1，1），对称轴是直线x＝﹣1，∵P（m，n）到y轴的距离小于2，∴﹣2＜m＜2，而﹣1﹣（﹣2）＜2﹣（﹣1），当m＝2，n＝（2+1）2+1＝10，当m＝﹣1时，n＝1，∴n的取值范围是1≤n＜10，故答案为：1≤n＜10．14．（2022•长春）已知二次函数y＝﹣x2﹣2x+3，当a≤x≤时，函数值y的最小值为1，则a的值为．【分析】函数配方后得y＝﹣x2﹣2x+3＝﹣（x+1）2+4，当y＝1时，﹣（x+1）2+4＝1，可得x＝﹣1±，因为﹣1+＞，所以﹣1﹣≤x≤时，函数值y的最小值为1，进而可以解决问题．【解答】解：∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，∴图象开口向下，顶点坐标为（﹣1，4），根据题意，当a≤x≤时，函数值y的最小值为1，当y＝1时，﹣（x+1）2+4＝1，∴x＝﹣1±，∵﹣1+＞，∴﹣1﹣≤x≤时，函数值y的最小值为1，∴a＝﹣1﹣．故答案为：﹣1﹣．15．（2022•黔东南州）若二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则一次函数y＝ax+b与反比例函数y＝﹣在同一坐标系内的大致图象为（）A．B．C．D．【分析】由抛物线开口方向，对称轴位置及抛物线与y轴交点位置判断a，b，c的符号，从而可得直线与反比例函数图象的大致图象．【解答】解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴在y轴左侧，∴b＞0，∵抛物线与y轴交点在x轴下方，∴c＜0，∴直线y＝ax+b经过第一，二，三象限，反比例函数y＝﹣图象经过一，三象限，故选：C．16．（2022•湖北）二次函数y＝（x+m）2+n的图象如图所示，则一次函数y＝mx+n的图象经过（）A．第一、二、三象限B．第一、二、四象限C．第一、三、四象限D．第二、三、四象限【分析】由抛物线顶点式可得抛物线顶点坐标，由图象可得m，n的符号，进而求解．【解答】解：∵y＝（x+m）2+n，∴抛物线顶点坐标为（﹣m，n），∵抛物线顶点在第四象限，∴m＜0，n＜0，∴直线y＝mx+n经过第二，三，四象限，故选：D．17．（2022•南充）已知点M（x1，y1），N（x2，y2）在抛物线y＝mx2﹣2m2x+n（m≠0）上，当x1+x2＞4且x1＜x2时，都有y1＜y2，则m的取值范围为（）A．0＜m≤2B．﹣2≤m＜0C．m＞2D．m＜﹣2【分析】根据题意和题目中的抛物线，可以求得抛物线的对称轴，然后分类讨论即可得到m的取值范围．【解答】解：∵抛物线y＝mx2﹣2m2x+n（m≠0），∴该抛物线的对称轴为直线x＝﹣＝m，∵当x1+x2＞4且x1＜x2时，都有y1＜y2，∴当m＞0时，0＜2m≤4，解得0＜m≤2；当m＜0时，2m＞4，此时m无解；由上可得，m的取值范围为0＜m≤2，故选：A．18．（2022•呼和浩特）在平面直角坐标系中，点C和点D的坐标分别为（﹣1，﹣1）和（4，﹣1），抛物线y＝mx2﹣2mx+2（m≠0）与线段CD只有一个公共点，则m的取值范围是．【分析】根据抛物线求出对称轴x＝1，y轴的交点坐标为（0，2），顶点坐标为（1，2﹣m），直线CD的表达式y＝﹣1，分两种情况讨论：m＞0时或m＜0时，利用抛物线的性质分析求解．【解答】解：抛物线的对称轴为：x＝﹣＝1，当x＝0时，y＝2，∴抛物线与y轴的交点坐标为（0，2），顶点坐标为（1，2﹣m），直线CD的表达式y＝﹣1，当m＞0时，且抛物线过点D（4，﹣1）时，16m﹣8m+2＝﹣1，解得：m＝﹣（不符合题意，舍去），当抛物线经过点（﹣1，﹣1）时，m+2m+2＝﹣1，解得：m＝﹣1（不符合题意，舍去），当m＞0且抛物线的顶点在线段CD上时，2﹣m＝﹣1，解得：m＝3，当m＜0时，且抛物线过点D（4，﹣1）时，16m﹣8m+2＝﹣1，解得：m＝﹣，当抛物线经过点（﹣1，﹣1）时，m+2m+2＝﹣1，解得：m＝﹣1，综上，m的取值范围为m＝3或﹣1＜m≤﹣，故答案为：m＝3或﹣1＜m≤﹣．19．（2022•包头）已知实数a，b满足b﹣a＝1，则代数式a2+2b﹣6a+7的最小值等于（）A．5B．4C．3D．2【分析】由题意得b＝a+1，代入代数式a2+2b﹣6a+7可得（a﹣2）2+5，故此题的最小值是5．【解答】解：∵b﹣a＝1，∴b＝a+1，∴a2+2b﹣6a+7＝a2+2（a+1）﹣6a+7＝a2+2a+2﹣6a+7＝a2﹣4a+4+5＝（a﹣2）2+5，∴代数式a2+2b﹣6a+7的最小值等于5，故选：A．20．（2022•贺州）已知二次函数y＝2x2﹣4x﹣1在0≤x≤a时，y取得的最大值为15，则a 的值为（）A．1B．2C．3D．4【分析】先找到二次函数的对称轴和顶点坐标，求出y＝15时，x的值，再根据二次函数的性质得出答案．【解答】解：∵二次函数y＝2x2﹣4x﹣1＝2（x﹣1）2﹣3，∴抛物线的对称轴为x ＝1，顶点（1，﹣3），∴当y ＝﹣3时，x ＝1，当y ＝15时，2（x ﹣1）2﹣3＝15，解得x ＝4或x ＝﹣2，∵当0≤x ≤a 时，y 的最大值为15，∴a ＝4，故选：D ．21．（2022•嘉兴）已知点A （a ，b ），B （4，c ）在直线y ＝kx +3（k 为常数，k ≠0）上，若ab 的最大值为9，则c 的值为（ ）A ．1B ．23C ．2D ．25 【分析】由点A （a ，b ），B （4，c ）在直线y ＝kx +3上，可得，即得ab ＝a （ak +3）＝ka 2+3a ＝k （a +）2﹣，根据ab 的最大值为9，得k ＝﹣，即可求出c ＝2．【解答】解：∵点A （a ，b ），B （4，c ）在直线y ＝kx +3上，∴，由①可得：ab ＝a （ak +3）＝ka 2+3a ＝k （a +）2﹣， ∵ab 的最大值为9，∴k ＜0，﹣＝9，解得k ＝﹣，把k ＝﹣代入②得：4×（﹣）+3＝c ，∴c ＝2，故选：C ．22．（2022•凉山州）已知实数a 、b 满足a ﹣b 2＝4，则代数式a 2﹣3b 2+a ﹣14的最小值是 ．【分析】根据a ﹣b 2＝4得出b 2＝a ﹣4，代入代数式a 2﹣3b 2+a ﹣14中，然后结合二次函数的性质即可得到答案．【解答】解：∵a ﹣b 2＝4，∴b2＝a﹣4，∴原式＝a2﹣3（a﹣4）+a﹣14＝a2﹣3a+12+a﹣14＝a2﹣2a﹣2＝a2﹣2a+1﹣1﹣2＝（a﹣1）2﹣3，∵1＞0，又∵b2＝a﹣4≥0，∴a≥4，∵1＞0，∴当a≥4时，原式的值随着a的增大而增大，∴当a＝4时，原式取最小值为6，故答案为：6．。

初二数学下册二次函数的解析式与像练习题二次函数作为数学中重要的概念之一，是初中数学教学中的重点内容。

在初二数学下册，学生将进一步学习二次函数的解析式和像，并通过练习题巩固所学知识。

本文将详细介绍二次函数的解析式和像，并提供相关练习题供学生练习。

一、二次函数的解析式二次函数是指变量的平方项系数不为零的函数，一般形式为f(x) =ax² + bx + c，其中a、b、c为实数且a≠0。

在二次函数中，常见的解析式有标准式和一般式。

1. 标准式标准式是二次函数的一种常见形式，其解析式可以表示为f(x) = a(x - h)² + k，其中a为抛物线的开口方向和大小，(h, k)为抛物线的顶点坐标。

例如，对于二次函数f(x) = 2(x - 3)² + 5，其中a = 2，(h, k) = (3, 5)，从解析式可以得知该二次函数向上开口，顶点坐标为(3, 5)。

2. 一般式一般式也是二次函数的一种常见形式，其解析式为f(x) = ax² + bx + c，其中a、b、c为实数且a≠0。

例如，对于二次函数f(x) = 2x² + 3x + 1，可以从解析式中得知a = 2，b = 3，c = 1。

二、二次函数的像二次函数的像即函数的值域，也就是函数在定义域内的所有可能的取值。

对于二次函数f(x) = ax² + bx + c，其像的范围与抛物线的开口方向有关。

1. 开口向上的二次函数当二次函数的a值大于0时，抛物线向上开口，此时函数的像的范围是从顶点值开始的上方所有实数。

例如，对于二次函数f(x) = 2(x - 3)² + 5，因为a = 2大于0，所以函数的像的范围是从顶点值开始的上方所有实数。

2. 开口向下的二次函数当二次函数的a值小于0时，抛物线向下开口，此时函数的像的范围是从顶点值开始的下方所有实数。

例如，对于二次函数f(x) = -2(x - 3)² + 5，因为a = -2小于0，所以函数的像的范围是从顶点值开始的下方所有实数。

二次函数的图像与性质【十大题型】【题型1 根据二次函数解析式判断其性质】 (3)【题型2 二次函数y=ax 2+bx+c 的图象和性质】 (4)【题型3 二次函数平移变换问题】 (5)【题型4 根据二次函数的对称性求字母的取值范围】 (6)【题型5 根据二次函数的性质求最值】 (6)【题型6 根据二次函数的最值求字母的取值范围】 (7)【题型7 根据二次函数自变量的情况求函数值的取值范围】 (7)【题型8 根据二次函数的增减性求字母的取值范围】 (8)【题型9 二次函数图象与各项系数符号】 (8)【题型10 二次函数与三角形相结合的应用方法】 (11)【知识点 二次函数的图像与性质】1.定义：一般的，形如y =ax 2+bx +c (a .b .c 是常数，a ≠0)的函数叫做二次函数。

其中x 是自变量，a .b .c 分别是函数解析式的二次项系数.一次项系数.常数项。

二次函数解析式的表示方法(1)一般式：y ＝ax 2＋bx ＋c (其中a ，b ，c 是常数，a ≠0)；(2)顶点式：y ＝a (x －h )2＋k (a ≠0)，它直接显示二次函数的顶点坐标是(h ，k )；(3)交点式：y ＝a (x －x 1)(x －x 2)(a ≠0)，其中x 1，x 2是图象与x 轴交点的横坐标 ．注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -³时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.2.二次函数的图象是一条抛物线。

当a ＞0时，抛物线开口向上；当a ＜0时，抛物线开口向下。

|a |越大，抛物线的开口越小；|a |越小，抛物线的开口越大。

y =ax 2y =ax 2+k y =a (x -h )2y =a (x -h )2+k y =ax 2+bx +c 对称轴y 轴y 轴x =h x =h abx 2-=(0，0)(0，k )(h ，0)(h ，k )⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22顶点a >0时，顶点是最低点，此时y 有最小值；a <0时，顶点是最高点，此时y 有最大值。