下载文档原格式
1、空间任意力系的简化与平衡
（1）空间任意力系向一点O简化，可得到一个主矢和主矩。
主矢等于力系中各力的矢量和，即
其作用线通过简化中心O，主矩等于力系中各力向简化中心O平移时产生的附加力偶矩与力系中已知的力偶矩之矢量和，即
主矢与简化中心的位置无关，主矩一般与简化中心的位置有关。
（2）空间任意力系的平衡方程
即力系中各力在x,y,z轴上投影的代数和分别为零，及力系中各力对x,y,z 轴之矩的代数和分别为零。
空间任意力系平衡方程的投影方程也可以用力矩方程代替，但独立的平衡方程只有六个，至多能求解六个未知量。
（3）几种特殊空间力系的平衡方程：
a）空间汇交力系平衡方程
b）空间平行力系的平衡方程c）空间力偶系的平衡方程
2、物体重心的坐标式。
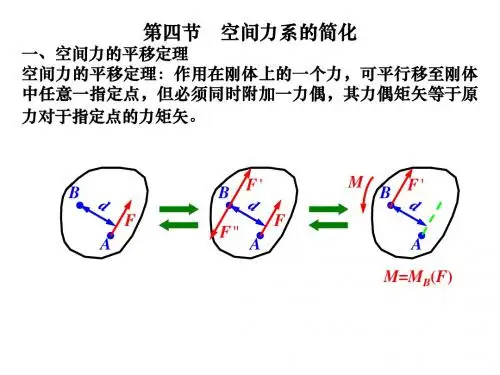
空间力系的简化RR F F F F F F F F =++=++=321'3'2'1')()()(321F M F M F M M o o o o ++=力系主矢: R F 力系主矩: oM 空间任意力系=主矢+主矩力系简化结果讨论:0=∑=i R F F )(])[()(i Ai i BA i Ai BA i Bi B F r F r F r r F r M ⨯+⨯∑=⨯+∑=⨯∑=AA i BA M M F r +=+∑⨯=01）F R =0、M O =0。
原力系是平衡力系。
2）F R =0、M O ≠0。
原力系等效于一个力偶。
力偶矩是自由矢量，可以平移到空间任意位置而不改变作用效果，所以主矢为零时主矩是一个与简化点位置无关的常量3）F R ≠0、M O =0。
原力系等效于一个力，该力经过简化点，称为原力系的合力。
)(≠∑=i A A F M M力系简化结果讨论:4.1）o R M F ⊥ROA OA O O F r F r F M M ⨯=⨯==)(4）F R ≠0、M O ≠0。
这是最一般的情况，又可细分为以下三种类型：4.2）F R ∥M O 。
主矢力F R 垂直于主矩力偶M O 中两力（F 1、F 1′）所在的平面，这时主矢力与主矩力偶怎么才能化简为一个力？力系简化结果讨论:空间力系的简化4.2）F R ∥M O 。
但力偶矩是自由矢量，可以把主矩M O 平移到主矢力F R 作用线上（图示），从而得到一个力螺旋：力螺旋由一个力和一个力偶构成，且力矢量与力偶矩矢量重合（即：力垂直于力偶中两力所在的平面）。
力螺旋对物体的作用效果是力与力偶作用效果的叠加（平移加旋转），如钻孔时钻头对工件的作用力就是力螺旋，拧螺钉时螺丝刀对螺钉的作用力也是力螺旋。
力螺旋不能再继续简化，它可以表示成图c 、d 所示任一形式。
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）力系简化结果讨论://O O O M M M -=⊥2//)()()cos (RR R O R R R R O R R O O F F F M F F F F M F F M M ⋅⋅=⋅⋅=⋅=α4.3）F R 既不平行也不垂直于M O 。
