空间任意力系的简化结果分析

力的作用点。

（在力的作用下，任意两静力学各知识点总结1. 静力学是研究物体在力系作用下的平衡规律的科学。

2. 力的三要素：（1）力的大小；（2）力的方向；（3）3. 力的效应：（1）外效应——改变物体运动状态的效应4.刚体：在外界任何作用下形状和大小都始终保持不变的物体。

点间的距离保持不变的物体）5.一个物体能否视为刚体，不仅取决于变形的大小，而且和问题本身的要求有关。

6.力：物体间相互的机械作用，这种作用使物体的机械运动状态发生变化。

7.力系：作用在物体上的一群力。

（同一物体）8.如果一个力系作用于物体的效果与另一个力系作用于该物体的效果相同，这两个力系 互为等效力系。

9.不受外力作用的物体可称其为受零力系作用。

一个力系如果与零力系作用等效，则该力系称为平衡力系。

10. 力应以矢量表示。

用 F 表示力矢量，用 F 表示力的大小。

在国际单位制中，力的单位是N 或Kn 。

（2）内效应一一引起物体形变的效应第一章•静力学公理F R = F I +F 2公理1:力的平行四边形法则作用在物体上同一点的两个力，可以合成为一个合力。

合力的作用点也在该点，合力的大小和方向，由这两个力为边构成的平行四边形的对角线确定。

公理2 :二力平衡条件作用在刚体上的两个力，使刚体保持平衡的必要和充分条件是：这两个力的大小相 等，方向相反，且作用在同一直线上。

公理3 :加减平衡力系原则在已知力系上加上或减去任意的平衡力系，与原力系对刚体的作用等效。

推理1 :作用于刚体上某点的力，可以沿着它的作用线移到刚体内任意一点，并不改变该推理2 :三力平衡汇交定理作用于刚体上三个相互平衡的力，若其中两个力的作用线汇交于一点，则此三力必在同一平面内，且第三个力的作用线通过汇交点。

4.线，5. 柔索类约束：绳索对物体的约束力，作用在接触点, ，沿着同一直线,公理4 :作用力与反作用力总是同时存在，两力的大小相等、方向相反、分别作用在两个相互作用的物体上。

《简明理论力学》——哈尔滨工业大学第二版静力学第一章静力学公理和物体的受力分析静力学：即刚体静力学，是研究刚性物体在平衡时的受力状况。

静力学研究三个问题：（1）物体的受力分析；（2）力系的等效代换；（3）力系的平衡条件极其应用。

（一）静力学公理：（1）公理1 力的平行四边形法则(三角形法则)作用在物体上同一点的两个力，可以合成为一个合力。

合力的作用点也在该点，合力的大小和方向，由这两个力为边构成的平行四边形的对角线确定。

（2）公理2 二力平衡条件作用在刚体上的两个力，使刚体保持平衡的必要和充分条件是：这两个力的等值，相反，共线。

（3）公理3 加减平衡力系原理在已知力系上加上或减去任意的平衡力系，并不改变原力系对刚体的作用。

推理1 力的可传性作用于刚体上某点的力，可以沿着它的作用线移到刚体内任意一点，并不改变该力对刚体的作用。

推理2 “三力”平衡汇交定理作用于刚体上三个相互平衡的力，若其中两个力的作用线汇交于一点，则此三力必在同一平面内，且第三个力的作用线通过汇交点。

（4）公理4 作用和反作用定律作用力和反作用力总是同时存在，同时消失，等值、反向、共线，作用在相互作用的两个物体上。

（5）公理5 刚化原理若变形体在某一力系作用下处于平衡，则将此变形体刚化为刚体，其平衡状态保持不变。

（注：反之不一定成立。

因为使刚体平衡的充要条件，对变形体是必要的但非充分的。

）（二）约束和约束力自由体(free body)：位移不受限制的物体非自由体(constrained body)：位移受到某些限制的物体约束(constraint)：对非自由体的某些位移起限制作用的周围物体约束体(constraint body)：约束非自由体运动的物体。

约束力(constraint force)：约束体作用在非自由体上的力。

注：火车是非自由体，铁轨是约束体，铁轨作用在车轮上的力为约束力。

1、工程中常见的约束（1）光滑接触约束---具有光滑接触面（线、点）的约束约束力特点：作用点：在接触处方向：沿接触处的公法线并指向受力物体；（故称为法向约束力）（2）柔索类约束--由柔软的绳索、胶带或链条等构成的约束约束力方向：柔索对物体的约束力沿着柔索背向被约束物体。

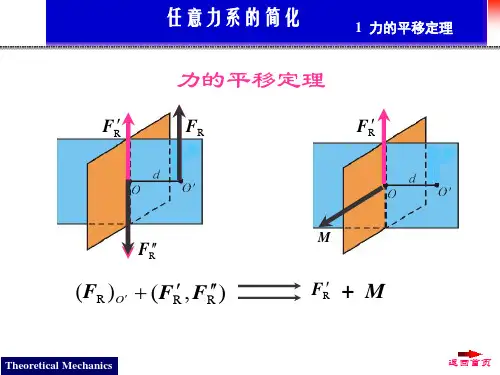
空间力系的简化RR F F F F F F F F =++=++=321'3'2'1')()()(321F M F M F M M o o o o ++=力系主矢: R F 力系主矩: oM 空间任意力系=主矢+主矩力系简化结果讨论:0=∑=i R F F )(])[()(i Ai i BA i Ai BA i Bi B F r F r F r r F r M ⨯+⨯∑=⨯+∑=⨯∑=AA i BA M M F r +=+∑⨯=01）F R =0、M O =0。

原力系是平衡力系。

2）F R =0、M O ≠0。

原力系等效于一个力偶。

力偶矩是自由矢量，可以平移到空间任意位置而不改变作用效果，所以主矢为零时主矩是一个与简化点位置无关的常量3）F R ≠0、M O =0。

原力系等效于一个力，该力经过简化点，称为原力系的合力。

)(≠∑=i A A F M M力系简化结果讨论:4.1）o R M F ⊥ROA OA O O F r F r F M M ⨯=⨯==)(4）F R ≠0、M O ≠0。

这是最一般的情况，又可细分为以下三种类型：4.2）F R ∥M O 。

主矢力F R 垂直于主矩力偶M O 中两力（F 1、F 1′）所在的平面，这时主矢力与主矩力偶怎么才能化简为一个力？力系简化结果讨论:空间力系的简化4.2）F R ∥M O 。

但力偶矩是自由矢量，可以把主矩M O 平移到主矢力F R 作用线上（图示），从而得到一个力螺旋：力螺旋由一个力和一个力偶构成，且力矢量与力偶矩矢量重合（即：力垂直于力偶中两力所在的平面）。

力螺旋对物体的作用效果是力与力偶作用效果的叠加（平移加旋转），如钻孔时钻头对工件的作用力就是力螺旋，拧螺钉时螺丝刀对螺钉的作用力也是力螺旋。

力螺旋不能再继续简化，它可以表示成图c 、d 所示任一形式。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）力系简化结果讨论://O O O M M M -=⊥2//)()()cos (RR R O R R R R O R R O O F F F M F F F F M F F M M ⋅⋅=⋅⋅=⋅=α4.3）F R 既不平行也不垂直于M O 。