第10章压杆稳定
- 格式:doc
- 大小:2.30 MB
- 文档页数:30









第10章压杆稳定学习目标:1.了解失稳的概念、压杆稳定条件及其实用计算;2.理解压杆的临界应力总图;3.掌握用欧拉公司计算压杆的临界荷载与临界应力。
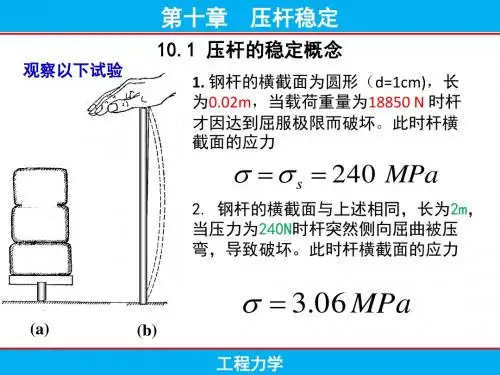
对承受轴向压力的细长杆,杆内的应力在没有达到材料的许用应力时,就可能在任意外界的扰动下发生突然弯曲甚至导致破坏,致使杆件或由之组成的结构丧失正常功能,此时杆件的破坏不是由于强度不够引起的,这类问题就是压杆稳定问题。
本章主要从压杆稳定的基本概念、不同支撑条件下的临界力、欧拉公式的适用条件以及提高压杆稳定性的措施方面加以介绍。
第一节压杆稳定的概念在研究受压直杆时,往往认为破坏原因是由于强度不够造成的,即当横截面上的正应力达到材料的极限应力时,杆才会发生破坏。
实验表明对于粗而短的压杆是正确的;但对于细长的压杆,情况并非如此。
细长压杆的破坏并不是由于强度不够,而是由于杆件丧失了保持直线平衡状态的稳定性造成的。
这类破坏称为压杆丧失稳定性破坏,简称失稳。
一、问题的提出工程结构中的压杆如果失稳,往往会引起严重的事故。
例如1907年加拿大魁北克圣劳伦斯河上长达548m的大铁桥,在施工时由于两根压杆失稳而引起倒塌,造成数十人死亡。
1909年,汉堡一个大型储气罐由于其支架中的一根压杆失稳而引起的倒塌。
这种细长压杆突然破坏,就其性质而言,与强度问题完全不同,杆件招致丧失稳定破坏的压力比招致强度不足破坏的压力要少得多,同时其失稳破坏是突然性,必须防范在先。
因而,对细长压杆必须进行稳定性的计算。
二、平衡状态的稳定性压杆受压后,杆件仍保持平衡的情况称为平衡状态。
压杆受压失稳后,其变形仍保持在弹性范围内的称为弹性稳定问题。
如图110-所示,两端铰支的细长压杆,当受到轴向压力时,如果是所用材料、几何形状等无缺陷的理想直杆,则杆受力后仍将保持直线形状。
当轴向压力较小时,如果给杆一个侧向干扰使其稍微弯曲,则当干扰去掉后,杆仍会恢复原来的直线形状,说明压杆处于稳定的平衡状态(如图)-所示)。
第10章 压杆的平衡稳定性与压杆设计刚体的平衡位形和弹性体的平衡状态都存在稳定与不稳定问题。
本章首先介绍关于弹性体平衡状态稳定性的基本概念,包括:平衡状态、平衡状态的分叉、分叉点、屈曲以及弹性平衡稳定性的静力学判别准则。
然后根据微弯的屈曲平衡状态,由平衡条件和小挠度微分方程以及端部约束条件,确定不同刚性支承条件下弹性压杆的临界力。
最后,本章还将介绍工程中常用的压杆稳定设计方法—安全因数法。
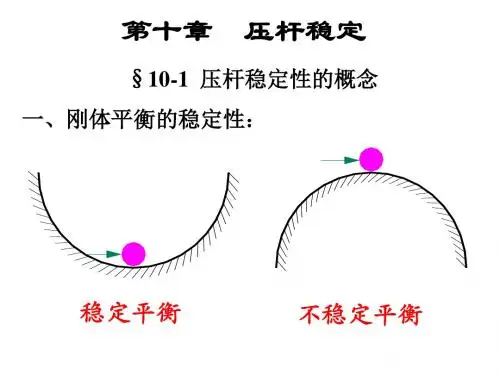
§10-1弹性体平衡状态稳定性的基本概念10-1-1 弹性稳定性的静力学判别准则结构构件或机器零件在压缩载荷或其他特定载荷作用下,在某一位置保持平衡,这一平衡位置又称为平衡状态(equilibrium configuration )。
当载荷小于一定的数值时,微小外界扰动(disturbance)使其偏离初始平衡状态;外界扰动除去后,构件仍能回复到初始平衡状态,则称初始平衡状态是稳定的(stable)当载荷大于一定的数值时,外界扰动使其偏离初始平衡状态,扰动除去后,构件不能回复到初始的平衡状态.则称初始的平衡状态是不稳定的(unstable )。
此即判别弹性稳定性的静力学准则(statical criterion for elastic stability )不稳定的平衡状态在任意微小的外界扰动下,都要转变为其他平衡状态,这种过程称为屈曲(buckling)或失稳(lost stability).通常,屈曲将导致构件失效,这种失效称为屈曲失效.由于这种失效具有突发性,常给工程带来灾难性后果.10-1-2 弹性压杆的平衡状态及分叉屈曲轴向受压的理想细长直杆(图10-1a),当轴向压力P F 小于某一数值,在任意小的扰动下使压杆偏离直线的平衡状态(例如发生微弯),扰动除去后,压杆又回到原来直线平衡状态,则称原来的直线平衡状态是稳定的。
这表明,当压力小于一定数值时,压杆只有直线一种平衡状态。
若以Δ表示压杆在屈曲时中间截面的侧向位移,则在P F Δ−坐标中当压力P F 小于某一数值时, P F Δ−关系由AB 竖直线所描述,如图10-1b 所示.(b)(a)图10-1 压杆的平衡路径当压力超过一定数值时,压杆仍可能具有直线的平衡状态,但在外界扰动下,使其偏离直线平衡状态,扰动除去后,不能再回到原来的直线平衡状态,而在某一弯曲状态下达到新的平衡,则称原来的直线平衡状态是“不稳定的”。
第10章压杆稳定10.1【学习基本要求】1、理解压杆稳定的稳定平衡、不稳定平衡、临界力的概念.2、掌握不同杆端约束下细长杆的临界力的计算公式.3、理解长度系数的意义,掌握与常见的几种约束形式对应的长度系数。
4、掌握临界力与压杆长度、横截面形状、杆端约束的关系。
5、理解压杆的柔度的概念,掌握柔度的计算方法。
6、明确欧拉公式的适用范围和临界应力计算。
7、熟练掌握大柔度杆、中柔度杆、小柔度杆的判别方法及临界应力总图。
8、掌握压杆的稳定条件。
9、能熟练运用安全系数法对不同柔度压杆的稳定性进行分析计算。
10、掌握提高压杆稳定性的措施。
10.2【要点分析】1、压杆稳定的概念稳定性:压杆能保持稳定的平衡性能称为压杆具有稳定性。
失稳:压杆不能保持稳定的平衡叫压杆失稳。
稳定平衡:细长杆在轴向压力下保持直线平衡状态,如果给杆以微小的侧向干扰力,使杆产生微小的弯曲,在撤去干扰力后,杆能够恢复到原有的直线平衡状态而保持平衡,这种原有的...直线平衡状态称为稳定平衡。
不稳定平衡:撤去干扰力后,杆不会回到原来的平衡,而是保持微弯或力F继续增大,杆继续弯曲,产生显著的变形,甚至发生突然破坏,则称原有的...平衡为不稳定平衡。
失稳:轴向压力F由小逐渐增大的过程中,压杆由稳定的平衡转变为不稳定的平衡,这种现象称为压杆丧失稳定性或压杆失稳。
临界平衡状态:压杆在稳定平衡和不稳定平衡之间的状态称为临界平衡状态。
临界压力或临界力:压杆由直线状态的稳定平衡过渡到不稳定平衡时所对应的轴向压力,称为压杆的临界压力或临界力.(即能使压杆保持微弯状态下的平衡的力)【注意】①临界状态也是一种不稳定平衡状态。
②临界状态下压杆即能在直线状态下也能在微弯状态下保持平衡。
③临界力使压杆保持微小弯曲平衡的最小压力.2、理想压杆理想压杆是指不存在初弯曲、初偏心、初应力的承受轴向压力的均匀连续、各向同性的直杆。
工程中实际压杆与理想压杆有很大的区别,因为实际压杆常常带有初始缺陷,如:①初弯曲的存在使压杆截面形心轴线不是理想直线;②初偏心的存在造成压力作用线与杆件轴线不重合;③残余应力造成材料内部留有初应力;④材质不可能是完全均匀连续的。
第10章 压杆稳定10.1【学习基本要求】1、理解压杆稳定的稳定平衡、不稳定平衡、临界力的概念。
2、掌握不同杆端约束下细长杆的临界力的计算公式。
3、理解长度系数的意义,掌握与常见的几种约束形式对应的长度系数。
4、掌握临界力与压杆长度、横截面形状、杆端约束的关系。
5、理解压杆的柔度的概念,掌握柔度的计算方法。
6、明确欧拉公式的适用范围和临界应力计算。
7、熟练掌握大柔度杆、中柔度杆、小柔度杆的判别方法及临界应力总图。
8、掌握压杆的稳定条件。
9、能熟练运用安全系数法对不同柔度压杆的稳定性进行分析计算。
10、掌握提高压杆稳定性的措施。
10.2【要点分析】1、压杆稳定的概念稳定性:压杆能保持稳定的平衡性能称为压杆具有稳定性。
失稳:压杆不能保持稳定的平衡叫压杆失稳。
稳定平衡:细长杆在轴向压力下保持直线平衡状态,如果给杆以微小的侧向干扰力,使杆产生微小的弯曲,在撤去干扰力后,杆能够恢复到原有的直线平衡状态而保持平衡,这种原有的...直线平衡状态称为稳定平衡。
不稳定平衡:撤去干扰力后,杆不会回到原来的平衡,而是保持微弯或力F 继续增大,杆继续弯曲,产生显著的变形,甚至发生突然破坏,则称原有的...平衡为不稳定平衡。
失稳:轴向压力F 由小逐渐增大的过程中,压杆由稳定的平衡转变为不稳定的平衡,这种现象称为压杆丧失稳定性或压杆失稳。
临界平衡状态:压杆在稳定平衡和不稳定平衡之间的状态称为临界平衡状态。
临界压力或临界力:压杆由直线状态的稳定平衡过渡到不稳定平衡时所对应的轴向压力,称为压杆的临界压力或临界力。
(即能使压杆保持微弯状态下的平衡的力)【注意】①临界状态也是一种不稳定平衡状态。
②临界状态下压杆即能在直线状态下也能在微弯状态下保持平衡。
③临界力使压杆保持微小弯曲平衡的最小压力。
2、理想压杆理想压杆是指不存在初弯曲、初偏心、初应力的承受轴向压力的均匀连续、各向同性的直杆。
工程中实际压杆与理想压杆有很大的区别,因为实际压杆常常带有初始缺陷,如:①初弯曲的存在使压杆截面形心轴线不是理想直线;②初偏心的存在造成压力作用线与杆件轴线不重合;③残余应力造成材料内部留有初应力;④材质不可能是完全均匀连续的。
这些缺陷不同程度的降低了压杆的稳定承载能力。
3、细长压杆的临界力细长压杆的临界力与杆件的长度、材料的力学性能、截面的几何性质和杆件两端的约束形式有关。
临界力计算公式称为欧拉公式,其统一形式为()20222c l EI l EI F r πμπ== (10.1) 【说明】①EI 为杆件的抗弯刚度;②l 0=μl 称为相当长度或计算长度,其物理意义为各种支承条件下,细长压杆失稳时挠曲线中相当于半波正弦曲线的一段长度,也就是挠曲线上两拐点间的长度,即各种支承情况下弹性曲线上相当于铰链的两点之间的距离;③μ称为长度系数,它反映了约束情况对临界力的影响,具体情况见表10-1。
4、细长压杆的临界应力压杆处于临界状态时横截面上的平均应力称为临界应力,用σcr 来表示。
压杆在弹性范围内的临界应力为22cr λπσE =A l EI A F cr 22)(μπ== (10.2) 【说明】①这是欧拉公式的另一种表达形式。
②EI 为杆件的抗弯刚度。
③I 、A 、i 2=I /A是只与杆横截面的形心主矩和截面面积,都是与截面形状和尺寸有关的几何量;④式中λ=μl /i 称为压杆的柔度或长细比,它全面地反映了压杆长度、约束条件、截面尺寸和形状对临界荷载的影响,是压杆的一个重要参数。
5、欧拉公式的适用范围欧拉公式是以压杆的挠曲线近似微分方程为依据而得到的,因此欧拉公式的适用条件是材料在线弹性范围内工作,即临界应力不超过材料的比例极限,即p 22cr σλπσ≤=E或 PσπλE ≥或P λλ≥ (10.3)【说明】①式中λ为压杆的柔度或长细比。
②式中P P /σπλE =,完全取决于材料的力学性质。
③满足λ≥λp 的压杆才能适用欧拉公式。
④适用欧拉公式的压杆称为细长杆或大柔度杆。
6、中长杆的临界应力1)直线公式对于中长杆,把临界应力与压杆的柔度表示成如下的线性关系。
λσb a cr -= (10.4)【说明】①式中a 、b 是与材料力学性质有关的系数,可以查相关手册得到。
②临界应力σcr 随着柔度λ的减小而增大。
③该式适用于P S λλλ<≤的压杆,称为中长杆或中柔度杆,式中b a S /)(S σλ-=,σS 为材料的屈服极限。
2)抛物线公式把临界应力cr σ与柔度λ的关系表示为如下形式()c c s cr a λλλλσσ≤⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-= 12 (10.5) 【说明】①式中σs 是材料的屈服强度。
②a 是与材料性质有关的系数。
③λc 是欧拉公式与抛物线公式适用范围的分界柔度。
7、粗短杆的临界应力当压杆的柔度满足λ<λs 条件时,这样的压杆称为粗短杆或小柔度杆。
实验证明,小柔度杆主要是由于应力达到材料的屈服强度(或抗压强度σb )而发生失效,属于强度问题。
8、临界应力总图 以柔度λ为横坐标,以临界应力σcr 为纵坐标,作出σcr -λ图,能够反映三类压杆的临界应力σcr 随压杆柔度λ变化的情况,称为临界应力总图。
图10-1所示的是中长杆采用直线公式的临界应力总图。
9、压杆稳定计算的安全系数法在对压杆进行稳定计算时,以临界应力除以大于1的安全系数所得的数值为准,即要求横截面上的正应力σ≤σcr /n st ,通常将稳定条件写成下列用安全系数表达的形式:st Ncr cr w n F Fn ≥==σσ (10.6)【说明】①式中,n st 为规定稳定安全系数。
②n w 称为压杆的工作安全系数。
③F N 是指压杆的轴力。
④σcr 和F cr 是指由临界应力总图得到的临界应力和临界力。
10、压杆稳定计算的折减系数法如果定义][][σϕσσ==stcrst n 为稳定许用应力,其中σcr 为压杆的临界应力,n st 为规定稳定安全系数,[σ]为强度计算时的许用应力。
ϕ称为折减系数,是一个小于1的数,是压杆长细比的函数,反映了随着压杆长细比的增加对稳定承载能力的降低。
因此,对于同种材料制成的等截面压杆,稳定条件可表达为][σϕσ≤=AFN w (10.7)式中,F N 为压杆轴向;A 为压杆的横截面面积。
【说明】①利用式(10.6)或式(10.7)就可进行稳定性校核、设计截面和确定许可荷载等三个方面的计算。
②需要指出的是,当压杆由于钉孔或其他原因而使截面有局部削弱时,因为压杆的临界力是根据整根杆的失稳来确定的,因此在稳定计算中不必考虑局部截面削弱的影响,而以毛面积进行计算。
③在强度计算中,危险截面为局部被削弱的截面,应按净面积进行计算。
11、提高压杆承载力的措施 影响压杆稳定性的因素有:压杆的截面形状,压杆的长度、约束条件和材料的性质等。
所以提高压杆承载能力的措施可以从选择合理的截面形式、减小压杆长度、改善约束条件及合理选用材料等几个方面着手。
10.3【范例讲解】例10-1图10-2所示两端球铰支承细长杆,弹性模量E =200GPa ,试用欧拉公式计算其临界力。
1)圆形截面,d =25 mm ,l =1.0 m ;图10-12)矩形截面,h =2b =40 mm ,l =1.0 m ; 3)No16工字钢,l =2.0 m 。
解:1)圆形截面杆:两端球铰: μ=1,()()4-8 422981221.910 m 6420010 1.91037.8 kN 11cr d I EI F l -π==⨯ππ⨯⨯⨯⨯===μ⨯ 2) 矩形截面杆:两端球铰:μ=1, I y <I z()()3-8 422982222.610 m1220010 2.61052.6 kN 11y y cr hb I EI F l ππμ-==⨯⨯⨯⨯⨯===⨯ 3) No16工字钢杆: 两端球铰:μ=1, I y <I z 查表I y =93.1×10-8 m 4()()22983222001093.110459 kN 12y cr EI F l ππμ-⨯⨯⨯===⨯ 例10-2图10-3所示矩形截面压杆,有三种支承方式。
杆长l =300 mm ,截面宽度b =20 mm ,高度h =12 mm ,弹性模量E =70 GPa ,λp =50,λ0=30,中柔度杆的临界应力公式为σcr =382 MPa – (2.18 MPa)λ。
试计算它们的临界力,并比较其大小。
解:(a)比较压杆弯曲平面的柔度:, , , ,y z y z y z y z y z l lI I i i i i μμλλλλ<<==⇒>长度系数: μ=2173.2y yli μλ==== 压杆是大柔度杆,用欧拉公式计算临界力;图10-2(b)(c) (a) A-A z 图10-3229()2270100.020.012 5.53 kN 173.2cr a cr y E F A A ππσλ⨯⨯=⨯=⨯=⨯⨯=(b)长度系数和失稳平面的柔度:10.31,86.60.012y yll i h μμλ⨯===== 压杆仍是大柔度杆,用欧拉公式计算临界力;229()2270100.020.01222.1 kN 86.6cr b cr y E F A A ππσλ⨯⨯=⨯=⨯=⨯⨯=(c)长度系数和失稳平面的柔度:0.5,43.3y yli μμλ===== 压杆是中柔度杆,选用经验公式计算临界力()6()(382 2.1843.3)100.020.1269.0kN cr c cr F A a b A σλ=⋅=-=-⨯⨯⨯⨯=三种情况的临界压力的大小排序为()()()cr a cr b cr c F F F <<。
例10-3图10-4所示压杆,截面有四种形式。
但其面积均为A =3.2×10 mm 2, 试计算它们的临界力,并进行比较。
弹性模量E =70 GPa ,λp =50,λ0=30,中柔度杆的临界应力公式为σcr =382 MPa – (2.18 MPa)λ。
解:(a)比较压杆弯曲平面的柔度:, , , y z y z y z y z yzllI I i i i i μμλλλλ<<==⇒>矩形截面的高与宽:222 3.210mm 4 mm 28 mm A b b b ==⨯∴==长度系数:μ=0.51299y yli μλ==== 压杆是大柔度杆,用欧拉公式计算临界力:(a)(c)(b)z 图10-42296()227010 3.2101014.6 N 1229cr a cr y E F A A ππσλ-⨯⨯=⋅=⋅=⨯⨯⨯= (b)计算压杆的柔度:正方形的边长:mm 24,mm 102.322=⨯=a a长度系数:μ=0.5918.6y z li μλλ===== 压杆是大柔度杆,用欧拉公式计算临界力:2296()227010 3.2101026.2 N 918.6cr b cr E F A A ππσλ-⨯⨯=⨯=⨯=⨯⨯⨯= (c)计算压杆的柔度:圆截面的直径:221 3.210 mm 6.38 mm 4d d π=⨯∴= 长度系数:μ=0.53440.53940.46.3810y z ll id μμλλ-⨯⨯=====⨯ 压杆是大柔度杆,用欧拉公式计算临界力:2296()227010 3.2101025 N 940.4cr c cr E F A A ππσλ-⨯⨯=⨯=⨯=⨯⨯⨯= (d)计算压杆的柔度:空心圆截面的内径和外径:2221[(0.7)] 3.210 mm 8.94 mm 4D D D π-=⨯∴= 长度系数:μ=0.5550y z i l i μλλ========== 压杆是大柔度杆,用欧拉公式计算临界力;2296()227010 3.2101073.1 N 550cr d cr E F A A ππσλ-⨯⨯=⋅=⋅=⨯⨯⨯= 四种情况的临界压力的大小排序为()()()()cr a cr c cr b cr d F F F F <<<。