第10章压杆稳定学习目标：1．了解失稳的概念、压杆稳定条件及其实用计算；2．理解压杆的临界应力总图；3．掌握用欧拉公司计算压杆的临界荷载与临界应力。
对承受轴向压力的细长杆，杆内的应力在没有达到材料的许用应力时，就可能在任意外界的扰动下发生突然弯曲甚至导致破坏，致使杆件或由之组成的结构丧失正常功能，此时杆件的破坏不是由于强度不够引起的，这类问题就是压杆稳定问题。
本章主要从压杆稳定的基本概念、不同支撑条件下的临界力、欧拉公式的适用条件以及提高压杆稳定性的措施方面加以介绍。
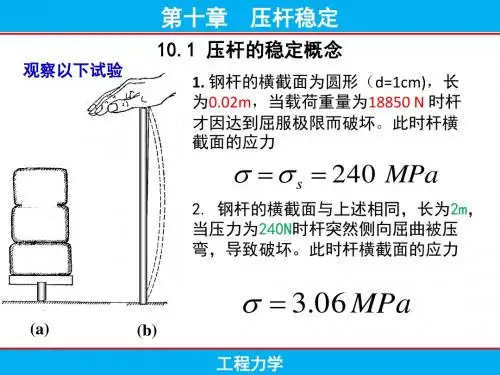
第一节压杆稳定的概念在研究受压直杆时，往往认为破坏原因是由于强度不够造成的，即当横截面上的正应力达到材料的极限应力时，杆才会发生破坏。
实验表明对于粗而短的压杆是正确的；但对于细长的压杆，情况并非如此。
细长压杆的破坏并不是由于强度不够，而是由于杆件丧失了保持直线平衡状态的稳定性造成的。
这类破坏称为压杆丧失稳定性破坏，简称失稳。
一、问题的提出工程结构中的压杆如果失稳，往往会引起严重的事故。
例如1907年加拿大魁北克圣劳伦斯河上长达548m的大铁桥，在施工时由于两根压杆失稳而引起倒塌，造成数十人死亡。
1909年，汉堡一个大型储气罐由于其支架中的一根压杆失稳而引起的倒塌。
这种细长压杆突然破坏，就其性质而言，与强度问题完全不同，杆件招致丧失稳定破坏的压力比招致强度不足破坏的压力要少得多，同时其失稳破坏是突然性，必须防范在先。
因而，对细长压杆必须进行稳定性的计算。
二、平衡状态的稳定性压杆受压后，杆件仍保持平衡的情况称为平衡状态。
压杆受压失稳后，其变形仍保持在弹性范围内的称为弹性稳定问题。
如图110-所示，两端铰支的细长压杆，当受到轴向压力时，如果是所用材料、几何形状等无缺陷的理想直杆，则杆受力后仍将保持直线形状。
当轴向压力较小时，如果给杆一个侧向干扰使其稍微弯曲，则当干扰去掉后，杆仍会恢复原来的直线形状，说明压杆处于稳定的平衡状态(如图)-所示)。
