剪切与挤压的实用计算共31页

第5章剪切和挤压的实用计算本章要点●掌握剪切的实用计算●掌握挤压的实用计算5.1剪切和剪切的实用计算5.1.1剪切的概念图5-1为一剪床剪切钢板的示意图，钢板在上、下刀刃的作用下，在相距δ区域内发生变形，当外力足够大时，钢板被切断。

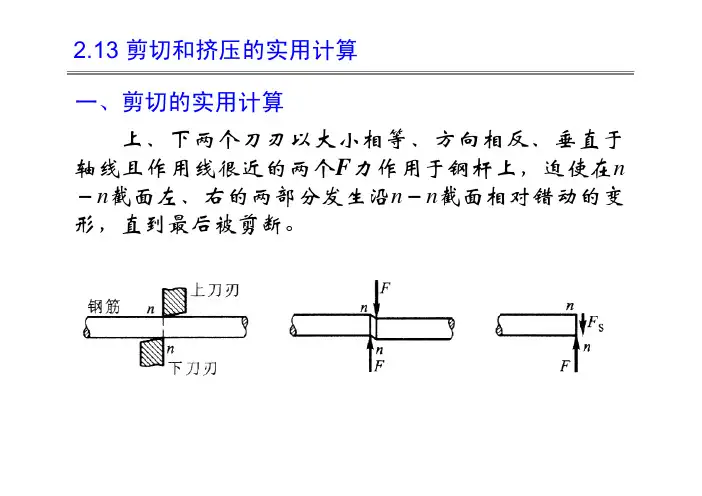
图5-1剪床剪钢板图5-2铆钉联接图5-2a为一铆钉联接简图。

当被联接件上受到外力F的作用后，力由两块钢板传到铆钉与钢板的接触面上，铆钉上受到大小相等，方向相反的两组分布力的合力F的作用(图5-2b)，使铆钉上下两部分沿中间截面m-m发生相对错动的变形，如图5-2c所示。

由上述两例，可见剪切的受力特点是：作用在杆件两侧面上且与轴线垂直的外力的合力大小相等，方向相反，作用线相距很近，其变形为使杆件两部分沿中间截面m-m在作用力的方向上发生相对错动。

杆件的这种变形称为剪切，杆件发生相对错动的中间截面m-m称为剪切面。

只有一个受剪面的剪切称为单剪，如上述两例。

有两个受剪面的剪切称为双剪，如图5-3中螺栓所受的剪切。

5.1.2剪切时的内力由截面法可得剪切面上的内力，它是剪切面上分布内力的合力，称为剪力，用F s表示（图5-4c）。

对任一分离体如（图5-4b、c）列平衡方程可得图5-3 两个受剪面F s=F图5-4剪切时的内力5.1.3剪切实用计算剪切面上分布内力的集度以τ表示，称为切应力（图5-4d）。

切应力在剪切面上分布的情况比较复杂。

为便于计算。

工程中通常采用以实验、经验为基础的实用计算，近似地认为切应力在受剪面内是均匀分布的(图5-4d)，按此假设计算出的切应力实质上是截面上的平均应力，称为名义切应力，即τ=F s/A s(5-1) 式中：τ——名义切应力Mpa，F s——剪切力N，A s——剪切面积mm2。

材料的极限切应力τu是按名义切应力概念，用试验方法得到的。

将此极限切应力除以适当的安全因数，即得材料的许用切应力[τ]=τu/n（5-2）式中：[τ]——许用切应力Mpa，τu——极限切应力Mpa，n——安全因数。

第3章剪切和挤压的实用计算3.1剪切的概念在工程实际中，经常遇到剪切问题。

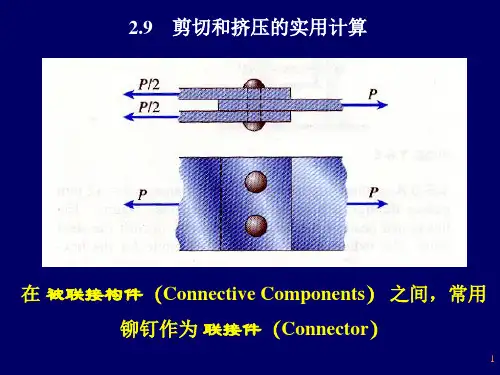
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用（图3-1a），构件的变形主要表现为沿着与外力作用线平行的剪切面（m - n面）发生相对错动（图3-1b）。

F,Hi |图3-1工程中的一些联接件，如键、销钉、螺栓及铆钉等，都是主要承受剪切作用的构件。

构件剪切面上的内力可用截面法求得。

将构件沿剪切面m—n假想地截开，保留一部分考虑其平衡。

例如，由左部分的平衡，可知剪切面上必有与外力平行且与横截面相切的内力F Q （图3-1c）的作用。

F Q称为剪力，根据平衡方程7丫=0，可求得F Q二F。

剪切破坏时，构件将沿剪切面（如图3-la所示的m-n面）被剪断。

只有一个剪切面的情况，称为单剪切。

图3-1a所示情况即为单剪切。

受剪构件除了承受剪切外，往往同时伴随着挤压、弯曲和拉伸等作用。

在图3-1中没有完全给出构件所受的外力和剪切面上的全部内力，而只是给出了主要的受力和内力。

实际受力和变形比较复杂，因而对这类构件的工作应力进行理论上的精确分析是困难的。

工程中对这类构件的强度计算，一般采用在试验和经验基础上建立起来的比较简便的计算方法，称为剪切的实用计算或工程计算。

3.2剪切和挤压的强度计算3.2.1剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。

图3-2a为一种剪切试验装置的简图，试件的受力情况如图3-2b所示，这是模拟某种销钉联接的工作情形。

当载荷F增大至破坏载荷F b时，试件在剪切面m-m及n-n处被剪断。

这种具有两个剪切面的情况，称为双剪切。

由图3-2c可求得剪切面上的剪力为F Q2-64 -图3-2由于受剪构件的变形及受力比较复杂，剪切面上的应力分布规律很难用理论方法确定，因而工程上一般采用实用计算方法来计算受剪构件的应力。

在这种计算方法中，假设应力在剪切面内是均匀分布的。

《工程力学》剪切与挤压的实用计算剪切和挤压是工程力学中两个非常重要的概念。

在工程实践中，往往需要对结构承受的剪切和挤压力进行计算，并通过计算结果来评估结构的稳定性和安全性。

本文将分别介绍剪切和挤压的概念和公式，并通过实例说明如何进行实用计算。

剪切是指力在结构内部沿着切面作用，导致结构内部产生剪应力和剪应变。

剪应力是垂直于切面方向的力与切面面积之比。

在工程实践中，常见的剪切力作用包括轴向力、剪力和扭矩。

对于轴向力和剪力，其剪应力可以通过下式计算：τ=F/A其中，τ为剪应力，F为作用力的大小，A为剪切面积。

对于扭矩作用，其剪应力的计算则需要考虑到截面形状和应力分布的不均匀性。

常见的情况是圆形截面的轴向受拉时的剪应力分布。

在这种情况下，剪应力的最大值出现在截面外圆周，可以通过下式进行计算：τ=T*r/I其中，τ为剪应力，T为扭矩的大小，r为截面距离外圆周的距离，I为截面的惯性矩。

挤压是指力在结构内部沿着压力方向作用，导致结构内部产生压应力和压应变。

挤压力作用常见于柱子或支撑结构的承重部分。

在计算挤压力时，首先需要确定结构的截面形状和尺寸。

然后可以通过下式计算挤压应力：σ=F/A其中，σ为挤压应力，F为挤压力的大小，A为截面积。

在实际工程中，剪切和挤压的计算往往需要考虑到结构的复杂性和非线性等因素。

此时，可以通过使用数值计算方法或专业软件进行计算，来得到更准确的结果。

此外，还需要根据结构的特点和工程要求，对计算结果进行适当的修正和调整。

举个例子来说明剪切和挤压的实用计算。

假设有一根圆柱形的支撑柱，柱子的直径为10cm，高度为2m。

假设柱子受到的挤压力为5000N。

1.根据柱子的直径计算出柱子的截面积：A = π * r^2 = π * (5cm)^2 = 78.54cm^22.将挤压力代入公式，计算出挤压应力：σ = F / A = 5000N / 78.54cm^2 = 63.73N/cm^2通过这个例子可以看出，挤压力的计算相对简单，只需要确定结构的截面形状和尺寸，并代入公式即可。