第6讲 剪切与挤压的实用计算

剪切和挤压的实用计算剪切和挤压是物理学中涉及材料力学行为的重要概念，广泛应用于工程设计、建筑结构、材料研究等领域。

在实际计算过程中，我们常常需要计算材料的剪切和挤压行为，以便更好地理解和预测材料在受力情况下的行为。

本文将介绍剪切和挤压的基本概念，并给出一些实用计算方法。

1.剪切：剪切是指在两个相对运动的平行平面之间的相对滑动，它是由垂直于平行平面的力引起的。

剪切力是使剪切发生的原因，剪切应力是由剪切力引起的应力。

剪切应力的计算公式为：τ=F/A其中，τ是剪切应力，F是作用在平行面上的剪切力，A是剪切应力作用的面积。

剪切应变的计算公式为：γ=Δx/h其中，γ是剪切应变，Δx是平行面滑动的位移，h是剪切应变的高度。

2.挤压：挤压是指在一个封闭容器中向内施加的力，使材料在容器内受到压缩。

挤压力是导致挤压发生的原因，挤压应力是由挤压力引起的应力。

挤压应力的计算公式为：σ=F/A其中，σ是挤压应力，F是作用在挤压面上的挤压力，A是挤压应力作用的面积。

挤压应变的计算公式为：ε=ΔL/L其中，ε是挤压应变，ΔL是受挤压材料的长度变化，L是原始长度。

3.实用计算：在实际计算中，我们往往需要确定材料的剪切和挤压强度，以及材料的最大变形能力。

剪切强度的计算方法：根据材料的剪切应力，选择适当的试验方法来测量剪切强度。

常用的试验方法有剪切强度试验和拉伸试验。

挤压强度的计算方法：根据材料的挤压应力，选择适当的试验方法来测量挤压强度。

常用的试验方法有挤压试验和压缩试验。

变形能力的计算方法：根据材料的剪切应变和挤压应变，通过试验测量材料的最大变形能力。

常用的试验方法有拉伸试验、压缩试验和剪切试验。

在计算过程中，需要考虑材料的应变硬化和弹塑性行为，并结合材料力学理论进行计算。

总结：剪切和挤压的实用计算是工程设计和材料研究中的重要环节。

通过计算剪切应力、剪切应变、挤压应力和挤压应变，可以更好地了解材料在受力情况下的行为，并为工程设计和材料选择提供依据。

第3章剪切和挤压的实用计算3.1剪切的概念在工程实际中，经常遇到剪切问题。

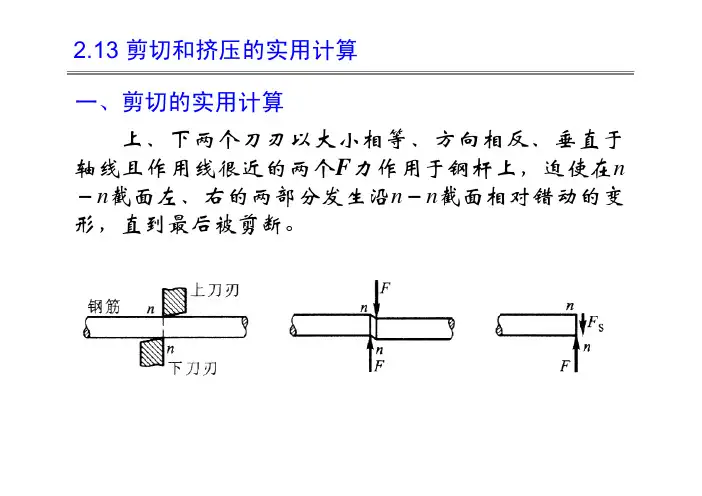
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用（图3-1a），构件的变形主要表现为沿着与外力作用线平行的剪切面（m - n面）发生相对错动（图3-1b）。

F,Hi |图3-1工程中的一些联接件，如键、销钉、螺栓及铆钉等，都是主要承受剪切作用的构件。

构件剪切面上的内力可用截面法求得。

将构件沿剪切面m—n假想地截开，保留一部分考虑其平衡。

例如，由左部分的平衡，可知剪切面上必有与外力平行且与横截面相切的内力F Q （图3-1c）的作用。

F Q称为剪力，根据平衡方程7丫=0，可求得F Q二F。

剪切破坏时，构件将沿剪切面（如图3-la所示的m-n面）被剪断。

只有一个剪切面的情况，称为单剪切。

图3-1a所示情况即为单剪切。

受剪构件除了承受剪切外，往往同时伴随着挤压、弯曲和拉伸等作用。

在图3-1中没有完全给出构件所受的外力和剪切面上的全部内力，而只是给出了主要的受力和内力。

实际受力和变形比较复杂，因而对这类构件的工作应力进行理论上的精确分析是困难的。

工程中对这类构件的强度计算，一般采用在试验和经验基础上建立起来的比较简便的计算方法，称为剪切的实用计算或工程计算。

3.2剪切和挤压的强度计算3.2.1剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。

图3-2a为一种剪切试验装置的简图，试件的受力情况如图3-2b所示，这是模拟某种销钉联接的工作情形。

当载荷F增大至破坏载荷F b时，试件在剪切面m-m及n-n处被剪断。

这种具有两个剪切面的情况，称为双剪切。

由图3-2c可求得剪切面上的剪力为F Q2-64 -图3-2由于受剪构件的变形及受力比较复杂，剪切面上的应力分布规律很难用理论方法确定，因而工程上一般采用实用计算方法来计算受剪构件的应力。

在这种计算方法中，假设应力在剪切面内是均匀分布的。

剪切与挤压的实用计算1.基本理论剪切是指沿着平面内条线上的应力沿剪切方向相对另一平面移位的力。

材料在受到剪切力作用时，会发生剪切变形并产生剪切应力。

剪切应力τ的计算公式为：τ=F/A其中，τ表示剪切应力，F表示受力，A表示受力面积。

材料的抗剪强度表示了材料在剪切载荷下破坏的抵抗能力，通常用剪切强度σs表示，剪切强度也可以通过横截面上的最大剪切应力来计算，即σs = τmax。

2.剪切计算方法在实际工程中，剪切常常涉及到材料的剪切强度计算、剪切连接件的设计以及剪切抗力的计算等。

（1）剪切强度计算根据材料的剪切性能参数，可以计算材料的抗剪强度。

一般来说，剪切强度与材料的抗拉强度有一定的关系。

对于金属材料来说，一般有以下公式用于计算剪切强度：σs=k·σu其中，σs表示材料的剪切强度，k表示剪切系数，一般取0.6~0.8，σu表示材料的抗拉强度。

（2）剪切连接件设计在机械设计中，常常需要设计剪切连接件，如销轴连接、键连接等。

设计剪切连接件时，需要根据剪切载荷和材料的强度参数来计算连接件的尺寸。

以销轴连接为例，假设在动力传动系统中，传递的扭矩为T，需设计一个销轴连接。

根据材料的抗剪强度和材料的弹性模量，可以计算出销轴的直径d。

d=[16·T/(π·τs)]^(1/3)其中，d表示销轴的直径，T表示扭矩，τs表示材料的抗剪强度。

（3）剪切抗力计算在工程结构设计中，剪切抗力的计算是非常重要的。

常见的剪切抗力计算方法有剪切弯曲理论、剪切流动理论等。

对于简支梁的剪切抗力计算来说，可以使用剪切弯曲理论。

根据弯矩与剪力之间的关系，可以得到梁上任意一点的剪切力V和弯矩M之间的关系：V = dM / dx其中，V表示剪切力，M表示弯矩，dM表示单位长度上的弯矩的变化，dx表示单位长度。

1.基本理论挤压是指沿轴线方向作用于材料上的静态或动态力。

当材料受到挤压力作用时，会发生长度方向的变形，并产生挤压应力。

第6讲教学方案——剪切与挤压的实用计算§2-13剪切和挤压的实用计算1．工程上的剪切件通过如图3-1所示的钢杆受剪和图3-2所示的联接轴与轮的键的受剪情况，可以看出，工程上的剪切件有以下特点：1）受力特点杆件两侧作用大小相等，方向相反，作用线相距很近的外力。

2）变形特点两外力作用线间截面发生错动，由矩形变为平行四边形。

(见动画：受剪切作用的轴栓)。

因此剪切定义为相距很近的两个平行平面内，分别作用着大小相等、方向相对（相反）的两个力，当这两个力相互平行错动并保持间距不变地作用在构件上时，构件在这两个平行面间的任一（平行）横截面将只有剪力作用，并产生剪切变形。

2．剪应力及剪切实用计算剪切实用计算中，假定受剪面上各点处与剪力Q 相平行的剪应力相等，于是受剪面上的剪应力为AQ=τ （3-1）式中：Q —剪力；A —剪切面积τ—名义剪切力剪切强度条件可表示为： []ττ≤=AQ（3-2） 式中：[]τ—构件许用剪切应力。

剪切面为圆形时，其剪切面积为：42d A π=对于如图3-3所示的平键，键的尺寸为l h b ⨯⨯，其剪切面积为：l b A ⋅=。

例2-14 电瓶车挂钩由插销联接，如图3-4a 。

插销材料为20#钢，[]MPa 30=τ，直径mm 20=d 。

挂钩及被联接的板件的厚度分别为mm 8=t 和mm 125.1=t 。

牵引力kN 15=P 。

试校核插销的剪切强度。

解：插销受力如图3-4b 所示。

根据受力情况，插销中段相对于上、下两段，沿m —m 和n—n 两个面向左错动。

所以有两个剪切面，称为双剪切。

由平衡方程容易求出2PQ =插销横截面上的剪应力为()[]τπτ<=⨯⨯⨯==-MPa 9.231020421015233A Q故插销满足剪切强度要求。

例2-15 如图3-8所示冲床，400max =P kN ，冲头[]400=σMPa ，冲剪钢板360=b τ MPa ，设计冲头的最小直径值及钢板厚度最大值。

《工程力学》剪切与挤压的实用计算剪切和挤压是工程力学中两个非常重要的概念。

在工程实践中，往往需要对结构承受的剪切和挤压力进行计算，并通过计算结果来评估结构的稳定性和安全性。

本文将分别介绍剪切和挤压的概念和公式，并通过实例说明如何进行实用计算。

剪切是指力在结构内部沿着切面作用，导致结构内部产生剪应力和剪应变。

剪应力是垂直于切面方向的力与切面面积之比。

在工程实践中，常见的剪切力作用包括轴向力、剪力和扭矩。

对于轴向力和剪力，其剪应力可以通过下式计算：τ=F/A其中，τ为剪应力，F为作用力的大小，A为剪切面积。

对于扭矩作用，其剪应力的计算则需要考虑到截面形状和应力分布的不均匀性。

常见的情况是圆形截面的轴向受拉时的剪应力分布。

在这种情况下，剪应力的最大值出现在截面外圆周，可以通过下式进行计算：τ=T*r/I其中，τ为剪应力，T为扭矩的大小，r为截面距离外圆周的距离，I为截面的惯性矩。

挤压是指力在结构内部沿着压力方向作用，导致结构内部产生压应力和压应变。

挤压力作用常见于柱子或支撑结构的承重部分。

在计算挤压力时，首先需要确定结构的截面形状和尺寸。

然后可以通过下式计算挤压应力：σ=F/A其中，σ为挤压应力，F为挤压力的大小，A为截面积。

在实际工程中，剪切和挤压的计算往往需要考虑到结构的复杂性和非线性等因素。

此时，可以通过使用数值计算方法或专业软件进行计算，来得到更准确的结果。

此外，还需要根据结构的特点和工程要求，对计算结果进行适当的修正和调整。

举个例子来说明剪切和挤压的实用计算。

假设有一根圆柱形的支撑柱，柱子的直径为10cm，高度为2m。

假设柱子受到的挤压力为5000N。

1.根据柱子的直径计算出柱子的截面积：A = π * r^2 = π * (5cm)^2 = 78.54cm^22.将挤压力代入公式，计算出挤压应力：σ = F / A = 5000N / 78.54cm^2 = 63.73N/cm^2通过这个例子可以看出，挤压力的计算相对简单，只需要确定结构的截面形状和尺寸，并代入公式即可。

剪切与挤压的实用计算工程构件中有许多构件往往要通过联接件联接。

所谓联接是指结构或机械中用螺栓、销钉、键、铆钉和焊缝等将两个或多个部件联接而成。

这些受力构件受力很复杂，要对这类构件作精确计算是十分困难的。

一、剪切 联接件一般受到剪切作用，并伴随有挤压作用。

剪切变形是杆件的基本变形之一，它是指杆件受到一对垂直于杆轴的大小相等、方向相反、作用线相距很近的力作用后所引起的变形，如图1（a ）所示。

此时，截面cd 相对于截面ab 将发生错动（滑移），如图1（b ）所示，即剪切变形。

若变形过大，杆件将在cd 面和ab 面之间的某一截面m-m 处被剪断，m-m 截面称为剪切面。

图1 杆件的剪切变形● 剪切的受力特点：一对大小相等、方向相反、作用线很近的、垂直于截面的力。

● 剪切的变形特点：两受力面发生相对错动。

由平衡条件可知，杆件受剪切时，剪切面上一定有一内力与外力相平衡，因此剪力Q 与外力F 的大小相等、方向相反、且都平行于截面。

注意到联接构件部位尺寸很小，受力又很复杂，若进行精确分析十分困难，工程中采用的是实用计算法。

AF =τ （1） 剪切强度条件为：[]ττ≤=AF （2） 二、挤压 挤压时两接触面上的压力称挤压力，用P iy 表示。

挤压力的大小等于外力，方向与外力方向相反。

联接件中产生挤压变形的表面称为挤压面。

图2 挤压 名义挤压应力公式为：jy jyjy A P =σ （3）式中，A jy 是挤压面面积。

当挤压面为平面接触时，挤压面积等于实际承压面积；当接触面为柱面时，挤压面积为实际面积在其直径平面上投影，其形状是一矩形，矩形的两个边长分别是圆柱体的直径和高度。

挤压强度条件为：[]jy jy jyjy A P σσ≤= （4）例：机车的联接如图，挂钩的厚度t =8mm ，销钉材料的许用切应力，许用挤压应力，牵引力，试选销直径。

（a ） （b ）解：销钉受力如图（b ）所示。

（1）根据剪切强度设计销钉直径。

剪切和挤压实用计算剪切和挤压是材料力学中常见的载荷形式，广泛应用于工程实践中。

剪切是指在材料中施加垂直于表面的切力，而挤压是指在材料中施加平行于表面的压力。

在工程设计和材料选择过程中，必须对剪切和挤压的载荷进行合理的计算，以确保结构和材料的安全性和可靠性。

本文将介绍剪切和挤压的实用计算方法，并提供一些实际应用案例，以帮助读者更好地理解和应用这些计算方法。

一、剪切的实用计算1.剪切力的计算剪切力是指作用在材料上的垂直于断面的力，可通过以下公式进行计算：剪切力=剪切应力×断面积其中，剪切应力是材料上的剪切应力，可以通过以下公式进行计算：剪切应力=剪切力/断面积2.剪切应力的计算剪切应力是剪切力对应的应力，即单位面积上的剪切力。

对于不同的材料，剪切应力的计算方法略有不同。

对于均匀材料，可以使用以下公式计算剪切应力：剪切应力=剪切力/断面积对于层合材料，由于材料的不同层之间可能存在剪切位移，剪切应力的计算较为复杂。

通常使用剪切力与剪切位移之间的关系来计算剪切应力。

3.剪切应变的计算剪切应变是指材料在受到剪切应力作用时产生的变形。

剪切应变的计算可以使用以下公式：剪切应变=切变角/材料长度其中，切变角可以通过材料变形前后标记点的位移计算得到。

二、挤压的实用计算1.挤压压力的计算挤压压力是指作用在材料上的平行于表面的压力，可以通过以下公式进行计算：挤压压力=挤压应力×断面积其中，挤压应力是指单位面积上的挤压力，可以通过以下公式进行计算：挤压应力=挤压压力/断面积2.挤压应力的计算挤压应力是指挤压压力对应的应力，即单位面积上的挤压力。

对于不同的材料，挤压应力的计算方法略有不同。

对于均匀材料，可以使用以下公式计算挤压应力：挤压应力=挤压压力/断面积对于复杂的材料结构，可以将材料分解为多个小单元，分别计算其挤压应力，再根据应力平衡原理计算整个结构的挤压应力。

3.挤压应变的计算挤压应变是指材料在受到挤压应力作用时产生的变形。

第6讲剪切与挤压的实用计算剪切和挤压是在工程中常用的加工方法，用于改变材料的形状和尺寸。

在实际应用中，经常需要对剪切和挤压进行计算，以确定加工参数和预测材料的变形和应力分布。

本文将介绍剪切和挤压的实用计算方法。

首先，我们来介绍剪切的实用计算方法。

剪切是指将材料切割成两块，其中一块固定不动，另一块沿切割面滑动。

剪切过程中，会产生剪力和剪应力。

剪切强度是指材料在剪切过程中所能承受的最大剪切应力。

剪切强度常用符号τ表示，其计算公式为：τ=F/A其中，F是作用在剪切平面上的力的大小，A是剪切平面的面积。

剪切强度是一个材料的重要指标，通常用于确定加工参数和材料选型。

在挤压方面，挤压是指将材料推入狭窄的空间中，通过外力的作用使其变形。

挤压过程中，会产生挤压压力和挤压应力。

挤压力是指挤压过程中的推力大小。

挤压力常用符号P表示，其计算公式为：P=F/A其中，F是作用在挤压材料上的力的大小，A是挤压材料的截面积。

挤压力是用来确定加工过程的关键参数，通常与模具设计和设备选型密切相关。

挤压应力是指挤压过程中材料的应力分布。

挤压应力的计算可以通过应力分析和有限元方法进行，这里不做详细介绍。

需要注意的是，挤压过程中应力集中和应力分布不均匀可能导致材料的断裂或变形，因此在工程中需要进行挤压力和挤压应力的合理计算和分析。

在实际应用中，剪切和挤压的计算可能会涉及到其他参数和力学模型，具体计算方法会根据具体情况而变化。

例如，在剪切过程中，需要考虑材料的变形和应力分布，所以可能需要使用材料力学和变形理论进行计算。

而在挤压过程中，需要考虑材料的变形和流动特性，所以可能需要使用流体力学和塑性变形理论进行计算。

总之，剪切和挤压的实用计算是工程中重要的一部分。

通过合理的计算和分析，可以确定加工参数和预测材料的变形和应力分布，为工程设计和生产提供依据，提高工作效率和生产质量。