监测接收机等效噪声温度分析
- 格式:doc
- 大小:28.00 KB
- 文档页数:4
噪声温度的测量增益法它是基于前面给出的噪声因数的定义:在这个定义中,噪声由两个因素产生。
一个是到达射频系统输入的干扰,与需要的有用信号不同。
第二个是由于射频系统载波的随机扰动(LNA ,混频器和接收机等)。
第二种情况是布朗运动的结果,应用于任何电子器件中的热平衡,器件的可利用的噪声功率为: P kT B这里的k = 波尔兹曼常量(1.38 * 10-23焦耳/K), T = 温度,单位为开尔文 B= 噪声带宽(Hz)在室温(290K)时,噪声功率谱密度P = -174dB m /H z ,因而我们有以下的公式: N out N F = P - ( -174dBm/H z + 20 * log10(BW ) +)增益 在公式中,N out P 是已测的总共输出噪声功率,-174dBm/Hz 是290K 时环境噪声的功率谱密度。
BW 是感兴趣的频率带宽(预选器中频带宽)。
Gain 是系统的增益。
NF 是DUT 的噪声系数。
公式中的每个变量均为对数。
为简化公式,我们可以直接测量输出噪声功率谱密度(dBm/Hz),这时公式变为:N out NF = P + 174dBm /Hz - Gain为了使用增益法测量噪声系数,DUT 的增益需要预先确定的。
DUT 的输入需要端接特性阻抗(射频应用为50,视频/电缆应用为75)。
输出噪声功率谱密度可使用频谱分析仪测量。
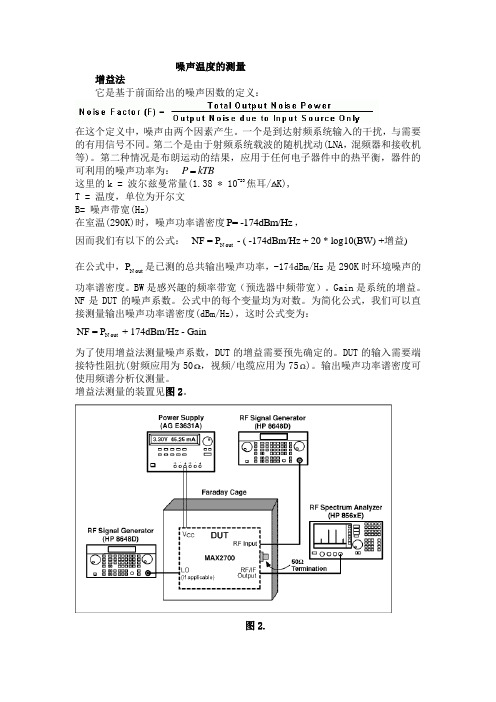
增益法测量的装置见图2。
图2.作为一个例子,我们测量MAX2700噪声系数的。
在指定的LNA 增益设置和V AGC 下测量得到的增益为80dB 。
接着,如上图装置仪器,射频输入用50负载端接。
在频谱仪上读出输出噪声功率谱密度为-90dBm/Hz 。
为获得稳定和准确的噪声密度读数,选择最优的RBW (解析带宽)与VBW(视频带宽)为RBW/VBW = 0.3。
计算得到的NF 为: -90dBm/Hz + 174dBm/Hz - 80dB = 4.0dB只要频谱分析仪允许,增益法可适用于任何频率范围内。

热噪声加性白高斯噪声(AWGN :Additive White Gaussian Noise )是最基本的噪声与干扰模型,通信中遇到的多数噪声和干扰都符合这个模型,其中最典型的是热噪声(Thermal Noise)。
一 电阻的热噪声将一个电阻从正中间画一条线分成上下两部分,那么线上的自由电子数和线下的自由电子数的数目是随机的,上下数目差也是随机的。
这个数目差意味着一个电动势,如果有闭合回路的话(如图4.8.2),就会形成一个随机电流,这就是热噪声。
叫热的原因是因为在绝对0度时,电子不运动,这样就不会有随机的电动势。
很显然,电阻的温度越高,随机性也就越强。
每个电子都在随机运动,上下数目差是这些电子随机运动的后果。
电子的总个数足以满足中心极限定律的条件,由此可知热噪声具有高斯的特征。
电子的运动速度极高。
相对于通信中的时间单位如ms 、µs 乃至ns 而言,在极短的一个时间间隔后,上下的电子数目已经毫不相关了,就是说热噪声的自相关函数对于我们的时间刻度来说是一个冲激函数,因此热噪声是一个白噪声。
综合这两点就是说:热噪声是白高斯噪声。
特别注意:白与高斯是两个单独的特征。
高斯是指一维分布,白由二维分布决定。
设()X t 是随机过程,下面的陈述A 涉及一维分布,陈述B 涉及二维分布。
A. 对X(t)进行了大量测试后发现,80%高于4.5,60%高于3.5;B .对X(t)同时观察相隔10秒的两个值()X t 和()10X t −,大量观察发现,在90%的情况下,()X t 与比10秒前相比,相差不会超过1±V ;在80%的情况下,相差不会超过±0.5V 。
物理学家告诉我们,热噪声的单边功率功率谱密度为0N KT =,其中231.3810K −=×是波尔兹曼常数,T 是绝对温度。
热噪声在带宽B 内的噪声功率KTB (本讲中所谈论的噪声功率均指在匹配负载上的可获功率)。


无线通信接收机的热噪声功率电平底噪分析无线通信接收机的热噪声功率电平底噪分析任何一个无线通信接收机能否正常工作,不仅取决于所能获得的输入信号的大小,而且也与其内部噪声以及外部噪声和干扰的大小有关。
接收机内部噪声也称为热噪声,它是由电子运动所产生的,其定义是指当温度为290?K(17?C)时,由接收机通带(通常由接收机中频带宽所决定)所截获的热噪声功率电平。
这个热噪声功率电平也称为接收机的底噪,是计算接收机的噪声的基本参数。
No=KTB(W)接收机带宽绝对温度值290?K玻尔兹曼常量1.37×10如用dBW表示,可写为No(dBw)=-204dBW+10lgB或=-174dBm+10lgB对于G网,B=200KHz(53dB),No=-121dBm通常决定无线接收机的灵敏度主要器件是输入射频放大器,因此,放大器的噪声系数也同样可用来衡量接收机灵敏度指标。
放大器噪声系数N=最大可能信噪比是把信号源内阻作为系统中唯一噪声源时输出端产生的信噪比,此时相当于负载开路状态;实测信噪比即将放大器的噪声与信号源内阻相加作为噪声源时输出端产生的信噪比。
所以N=式中:kTB-带宽为B(Hz)时的热噪声Ni-输入端噪声功率电平Na-放大器内部噪声功率电平g-放大器放大量以输入电动势表示的灵敏度(e)与N的关系可以表示为: e=式中:R为输入阻抗(50)N为接收机噪声系数B为噪声宽带(通常即接收机的中频带宽)C/N:为门限载噪比(通常与数据速率有关)在工程设计中,通常仅需知道接收机输入端(开路)的信号功率Pi(dBm)即Pi(dBm)===-174(dBm)+10lgB+N(dB)+C/N 对于G网,当B=200KHzN=4dBC/N=12dB时Pi(dBm)=-174+53+4+12 =-105dBm在扩频数字通信接收机中,链路的度量参数Eb/No(每比特能量与噪声功率谱密度的比值)与达到某预期接收机灵敏度所需的射频信号功率值的关系是从标准噪声系数F的定义中推导出来的。

目前主流接收机噪声测试方案分析
1.KEYSIGHT/R&S/Anristru等微波测试仪器巨头目前普遍采用噪声头(雪崩源)
+噪声分析仪
优点
✓测试速度快
缺点:
✓工作在140GHz以下,无法在太赫兹频段使用
✓重复性差
✓设备成本高
2.英国卢瑟福实验室,荷兰宇航局也采用泡在液氮中的吸波材料作为冷源+常
温黑体组合进行Y因值测试
优点
✓温差大,可以用于测试灵敏度较高的低温接收机
缺点:
✓测试精确度不高,液氮反射系数较高会增加测试误差
✓系统结构复杂,测试效率低
3.法国VIVA公司也采用低温杜瓦做作为冷源+常温黑体组合进行Y因值测试
优点
✓温差大,可以用于测试灵敏度较高的低温接收机
缺点:
✓测试精确度不高,低温波导出现结露结霜的问题直接影响测试灵敏度
✓系统结构复杂,设备成本高
4.航天203所自研CNAS系列液氮低温黑体作为冷源+常温黑体组合进行Y因
值测试
优点
✓温差大,可以用于测试灵敏度较高的低温接收机
缺点:
✓测试精确度不高,低温波导出现结露结霜的问题直接影响测试灵敏度
✓黑体材料反射特性不稳定,无法在太赫兹宽频段工作。
目前仅工作到220GHz ✓系统结构复杂,设备成本高
5.CHARLMES、ESA、NIST 、电子科技大学、中电13所、ALMA目前均采用TK
热源+常温黑体组合方案进行噪声测试
优点
✓精度高可追溯,校准黑体+测试黑体
✓自动化测试
✓国内有成功案列
缺点:
✓温差不够大,测试分辨率有待提高
✓对低温接收机的噪声测试无能为力。

接收机噪声系数测试方法(实用版4篇)篇1 目录1.引言2.噪声系数的定义和重要性3.传统噪声系数测量方法的局限性4.多通道射频接收机测量噪声系数的方法5.结论篇1正文接收机噪声系数测试方法是一种用于评估射频接收机性能的重要技术手段。
噪声系数是描述接收机前端放大器噪声特性的参数,它直接影响到接收机的灵敏度和信噪比。
因此,对接收机噪声系数的精确测量具有重要的实际意义。
一、引言射频接收机广泛应用于通信、广播、导航等领域,其性能指标直接影响到整个系统的性能。
噪声系数是描述接收机前端放大器噪声特性的参数,它直接影响到接收机的灵敏度和信噪比。
因此,对接收机噪声系数的精确测量具有重要的实际意义。
二、噪声系数的定义和重要性噪声系数(Noise Figure,NF)是指接收机前端放大器在输入信号一定时,输出信号噪声功率与输入信号噪声功率之比。
噪声系数越小,表示接收机前端放大器的噪声性能越好,灵敏度和信噪比越高。
因此,噪声系数是评估接收机性能的重要参数之一。
三、传统噪声系数测量方法的局限性传统的噪声系数测量方法主要包括噪声源法、噪声桥法和反射法等。
这些方法在测量低噪声系数的接收机时存在一定的局限性,主要表现在以下几个方面:1.测量范围有限:传统方法的测量范围通常在 100 MHz 以下,对于高频噪声系数的测量能力较弱。
2.测量精度受限:传统方法的测量精度受到噪声源、测试环境和被测器件等因素的影响,难以实现高精度测量。
3.测量时间较长:传统方法的测量时间通常较长,不利于高效、快速地评估接收机性能。
四、多通道射频接收机测量噪声系数的方法针对传统噪声系数测量方法的局限性,研究人员提出了多种针对多通道射频接收机的噪声系数测量方法。
这些方法主要利用多通道切换、噪声注入和数字信号处理等技术来实现高精度、高效率的噪声系数测量。
1.多通道切换测量法:通过设计多个射频开关,实现不同通道之间的切换,从而在不同通道切换的过程中测量噪声系数。
接收机射频热噪声分析摘要:本文首选介绍了电路噪声理论基础,通过建立了接收机射频通道的简化模型,推导了射频通道的噪声系数表达式,并分析了接收机射频通道的热噪声特性。
关键词:射频热噪音分析在电子系统中,噪声被用来描述附加在电信号上面的、任何不希望出现的扰动。
在无线电通信、雷达和导航系统中,信号传递过程的各个环节,都会附加各种各样的噪声。
这些噪声对通信、雷达和导航系统的性能起着制约作用。
实现低噪声设备的前提是发展电路噪声理论,设计低噪声电路及器件。
目前随着集成电路一类器件的发展及应用,对复杂电路的噪声分析计算以及设计,已经越来越具有重要性。
1接收机射频热噪声概述1.1热噪声含义在实际接收机系统中,由于自然或者人为的原因,存在各种起伏不定的随机的电压或者电流波动,这些波动叠加在有用信号上面会对系统的信息传递产生影响。
而这些随机的波动往往是人们不希望出现的,因此被称为噪声。
接收机输出的信号上面叠加的噪声一部分是在进入接收机前就已经具有的,称为外部噪声,另一部分是接收机内部产生的,称为内部噪声。
外部噪声是信号在传输介质中传播时引入的噪声,包括人为噪声、大气噪声和空间噪声等。
内部噪声是由接收机自身引入的,如电阻中的自由电子热运动引起的热噪声,晶体管中的载流子随机产生、复合和扩散引起的散弹噪声等,也称之为起伏噪声。
其中,热噪声是由于导体内部自由电子和振动粒子的热相互作用而产生的。
热相互作用导致电阻两端电子到达速度随机变化,因此电阻两端的电位差也随机变化,在某个值附近上下波动。
电子设备的电阻总会产生热噪声。
1.2热噪声特征1928年J.B.Johnson首先研究了热噪声,所以热噪声也被称为约翰逊噪声。
由于热噪声的频率可以覆盖全部频段,并且在整个频域的功率谱密度为一恒定值,因此也被称为白噪声。
一个阻值为R的电阻,在噪声频带宽度B内,产生的电压均方值是:一个实际电阻可以等效为一个理想电阻和一个电压源串联的形式,如图一(a)所示,其中R是无噪声的理想电阻,用戴维南定理可以将该电路变换为一个电阻和一个电流源并联的形式,如图一(b)所示。
热噪声加性白高斯噪声(AWGN :Additive White Gaussian Noise )是最基本的噪声与干扰模型,通信中遇到的多数噪声和干扰都符合这个模型,其中最典型的是热噪声(Thermal Noise)。
一 电阻的热噪声将一个电阻从正中间画一条线分成上下两部分,那么线上的自由电子数和线下的自由电子数的数目是随机的,上下数目差也是随机的。
这个数目差意味着一个电动势,如果有闭合回路的话(如图4.8.2),就会形成一个随机电流,这就是热噪声。
叫热的原因是因为在绝对0度时,电子不运动,这样就不会有随机的电动势。
很显然,电阻的温度越高,随机性也就越强。
每个电子都在随机运动,上下数目差是这些电子随机运动的后果。
电子的总个数足以满足中心极限定律的条件,由此可知热噪声具有高斯的特征。
电子的运动速度极高。
相对于通信中的时间单位如ms 、µs 乃至ns 而言,在极短的一个时间间隔后,上下的电子数目已经毫不相关了,就是说热噪声的自相关函数对于我们的时间刻度来说是一个冲激函数,因此热噪声是一个白噪声。
综合这两点就是说:热噪声是白高斯噪声。
特别注意:白与高斯是两个单独的特征。
高斯是指一维分布,白由二维分布决定。
设()X t 是随机过程,下面的陈述A 涉及一维分布,陈述B 涉及二维分布。
A. 对X(t)进行了大量测试后发现,80%高于4.5,60%高于3.5;B .对X(t)同时观察相隔10秒的两个值()X t 和()10X t −,大量观察发现,在90%的情况下,()X t 与比10秒前相比,相差不会超过1±V ;在80%的情况下,相差不会超过±0.5V 。
物理学家告诉我们,热噪声的单边功率功率谱密度为0N KT =,其中231.3810K −=×是波尔兹曼常数,T 是绝对温度。
热噪声在带宽B 内的噪声功率KTB (本讲中所谈论的噪声功率均指在匹配负载上的可获功率)。
监测接收机等效噪声温度分析
【摘要】文章从RDSS系统运行的实际情况出发,对地面监测接收机的热噪声进行了论述,引入了等效噪声温度的概念,并对级联网络的等效噪声温度给予了求解,在此基础上最后对RDSS系统地面监测接收机的等效噪声温度进行了分析和研究。
【关键词】接收机;热噪声;等效噪声温度
1.引言
由于RDSS系统采用卫星传输体制,用户入站信号在到达地面中心站前须经卫星转发,远距离传输后到达接收机的信号是很微弱的,如何使接收机的噪声尽可能低,从而使信号与噪声的功率比尽可能满足后端信号处理单元的工作要求,是系统设计的一个至关重要问题。
而从研究通信系统的角度看,接收机线性或准线性放大器、变频器以及线路的电阻损耗引起的噪声,均可以作为等效热噪声来处理,或者有的本身就是热噪声,所以文章从热噪声出发,引入等效噪声温度的概念,继而对级联网络的等效噪声温度进行求解,在此基础上对RDSS系统地面监测接收机的等效噪声温度给予分析。
2.热噪声基本概念
热噪声是由于传导媒质中带电粒子(通常是电子)随机运动而产生的。
其功率谱密度试验结果及热力学和量子力学的分析表明,阻值为R的电阻(或物体)其两端所呈现的热噪声电压,服从高斯分布,其均值为零,均方值为2R(πkT)2/3h,单位为(V2);而热噪声的单边功率谱密度N(f)为:
N(f)=4Rhf/(ehf/kT-1)(V2/Hz)(1)
式中,T为物体的绝对温度,(K);
k为波耳兹曼常数,1.38054×10-23 (J/K);
h为布朗克适量,6.6254×10-34(J·S);
f为频率(Hz)。
如图1所示,当此电阻与线性网络匹配连接即R=Rin时,热噪声源输出的是最大噪声功率。
匹配负载所得到的最大噪声单边功率谱密度,用n0表示,即:
n0=hf/(ehf/kT-1)(W/Hz)(2)
当f<<kT/h时,ehf/kT?1+hf/kT,则上式化简为:
n0=kT(W/Hz)(3)
从(3)式可以看出,此时的噪声单边功率谱密度n0与T成正比、与R无关,并且不随频率而变化,即呈现均匀谱,因而借用光谱的概念把f<<kT/h时的热噪声称之为白噪声。
由于线性网络总是有一定频带的,设Bn为线性网络的噪声等效带宽(Hz),则匹配负载得到的噪声功率N为:
N=kTBn(W)(4)
3.等效噪声温度的引入
在卫星通信中,我们遇到的大部分电路是线性的,因此我们可以用一个线性网络来描述。
无论是有源的线性网络如放大器、变频器,还是无源的线性网络如滤波器,其内部总是会不同程度地产生噪声。
这些内部噪声可能是热噪声也可能不是,而为了分析、设计线路的方便,我们希望能把它们统统等效成热噪声来处理,因而引入等效噪声温度的概念。
如图2左图所示,网络内部产生噪声。
把内部产生的噪声功率归算到网络的输入端,并用DN表示,则由(4)式,网络输出的噪声功率应为:
N=(kTiBn+DN)Gp (5)
式中kTiBn是输入端匹配电阻在环境温度为Ti条件下产生的输入热噪声功率;GP是网络最大功率增益。
我们假想有一个温度Te,如果一个输入匹配电阻在这个温度所产生白噪声功率正好等于上述附加的噪声功率DN,即:
DN=kTeBn (6)
那么,我们就称Te为等效噪声温度,也就是DN等效为由一个温度为Te的热噪声源产生的功率。
这样式(5)就可以写成:
N=kBnGp(Ti+Te)(7)
式中,Ti是物理温度,而Te则完全是一个等效的温度。
如果令:
Te’=Ti+Te (8)
则:
N=kT’BnGp (9)
即网络可看作是一个无噪声理想网络,所有噪声等效为输入匹配电阻在Te′温度时所产生的热噪声(参看图2)。
Te′为总的输入端等效噪声温度,利用它可比较两个或多个系统。
若两个系统的总等效噪声温度相同,即使外部或内部噪声情况不一样,这两个系统的灵敏度是相同的。
4.级联网络等效噪声温度的求解
考虑到地面监测接收机是一个级联网络,我们首先对级联网络总的等效噪声温度进行求解。
如图3所示,画出了3个网络级联的情况。
图中输入、输出及网络间均匹配连接,G、B、Te分别代表各网络的功率增益、噪声等效带宽、等效噪声温度,并用B1-2、B2-3分别标记第一、二两级及第二、三两级的总噪声等效带宽,B1-3则为三级的总噪声等效带宽。
这样,第一级网络的输出噪声功率为:
kB1G1(T1+Te1)
把它作为第二级网络的输入噪声功率,则第二级网络的噪声输出为:
kB1-2G1G2(T1+Te1)+kB2G2Te2
第三级的输出噪声功率为:
kB1-3G1G2G3(T1+Te1)+kB2-3G2G3Te2+kB3G3Te3 (10)
为了求级联网络总的输入端等效噪声温度Te,我们把三级网络看成一个增益为G1G2G3、噪声等效带宽为B1-3的网络,那么其输出噪声功率应为kB1-3G1G2G3(T1+Te)。
与(10)式直接比较可求得:
Te=Te1+Te2B2-3/G1B1-3+Te3B3/G1G2B1-3 (11)
5.RDSS系统监测接收机等效噪声温度分析
如图4所示,地面站接收机由低噪声放大器,下变频器,中频单元级联而成。
在这个级联网路中,低噪声放大器的带宽(约500MHz)大于下变频器的带宽(约40MHz),而下变频器的带宽又大于中频单元的带宽(约8MHz),即对于图3,满足B1≥B2≥B3。
这意味着前级输出噪声的频谱宽度大于后级网络的带宽,最后一级带宽最窄,故整个带宽决定于最后一级,可以把它看成是整个网络的带宽。
也就是对于(11)式,满足等式B1-3=B2-3=B3,故(11)式可化简为:Te=Te1+Te2/G1+Te3/G1G2 (12)
由(12)式可以看出,如果第一级网络(即低噪声放大器)的增益足够大,使得Te2/G1<<Te1,则整个网络的等效噪声温度将基本决定于第一级的等效噪声温度,即Te≈Te1,而后级(即下变频器,中放)的噪声影响就不是太大。
因此,由上面分析,我们可得出如下结论:为降低RDSS系统地面监测接收机的等效噪声温度Te,应降低接收机前端低噪声放大器的等效噪声温度,并使其有足够大的增益。
6.结束语
目前,从卫星导航系统需要出发,通过对热噪声基本概念、等效噪声温度的引入和级联网络等效噪声温度的求解,对RDSS系统监测接收机等效噪声温度进行了分析研究,决定该系统地面监测接收机前端低噪声放大器采用的是低噪声场效应晶体管放大器,其等效噪声温度约40K,增益约60分贝,它由六个管子级联而成,噪声性能好,增益高。
作为接收机的前端设备,低噪场放很好地完成了将天线接收到的微弱入站信号进行低噪声、高增益放大的任务,从而提高了整个RDSS系统的接收灵敏度。
参考文献
[1]C.Macabiau, E.Chatre.Impact of Evil Waveforms on GBAS Performance.Position Location and Navigation Symposium,IEEE PLANS,22-9,2000.
[2]A.J.Jakab.Quality Monitoring of GPS Signals.Master Degree.Calgary,Alberta.2001.
[3]T.J.Nagle.GPS Civil Monitoring Performance Specification.DOT-VNTSC-FAA-09-08,April 30,2009.
[4]付梦印,王美玲,吴江等.利用GPS卫星信号测量车辆航向[J].传感器世界,1997(1O):12-15.
[5]于国强,邱致和等.导航与定位[M].北京:国防工业出版社,2000:215-216.
[6]许其风.我国成功发射导航定位卫星[J].测绘信息与工程,2001.
[7]葛榜军,廖春发.卫星应用现状与发展(上册):总装备部卫星有效载荷及应用技术专业组应用技术分组[M].中国科学技术出版社,2001.。