二次函数中的存在性问题(平行四边形)ppt课件

专题：二次函数中的平行四边形存在性问题类型一：已知三个定点，再找一个定点构成平行四边形（平面内有三个点满足）1.已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0)，与y 轴的正半轴交于点C．⑴直接写出抛物线的对称轴，及抛物线与x 轴的另一个交点B 的坐标；⑵当点C 在以AB 为直径的⊙P 上时，求抛物线的解析式；⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A、B、C 为顶点的四边形是平行四边形？若存在,请求出点M 的坐标；若不存在,请说明理由．类型：已知两个定点，再找两个点构成平行四边形1．已知，如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点，与x 轴交于A、B 两点，A 点在B 点左侧。

点B 的坐标为(1，0),OC=30B．(1)求抛物线的解析式；(2)若点D 是线段AC 下方抛物线上的动点，求四边形ABCD 面积的最大值：(3)若点E 在x 轴上，点P 在抛物线上。

是否存在以A、C、E、P 为顶点且以AC 为一边的平行四边形?若存在，求点P 的坐标；若不存在，请说明理由．2、练习如图，抛物线：c bx x y ++=221与x 轴交于A、B（A 在B 左侧），顶点为C（1，﹣2）。

（1）求此抛物线的关系式；并直接写出点A、B 的坐标；（2）求过A、B、C 三点的圆的半径；（3）在抛物线上找点P，在y 轴上找点E，使以A、B、P、E 为顶点的四边形是平行四边形，求点P、E 的坐标。

1．如图，抛物线223y x x =--与x 轴交A、B 两点（A 点在B 点左侧），直线l 与抛物线交于A、C 两点，其中C 点的横坐标为2．（1）求A、B 两点的坐标及直线AC 的函数表达式；（2）P 是线段AC 上的一个动点，过P 点作y 轴的平行线交抛物线于E 点，求线段PE 长度的最大值；（3）点G 抛物线上的动点，在x 轴上是否存在点F，使A、C、F、G 这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F 点坐标；如果不存在，请说明理由．2、练习：如图，抛物线y=x2+bx+c的顶点为D（-1，-4），与y轴交于点C（0，-3），与x轴交于A，B 两点（点A在点B的左侧）。

二次函数中的平行四边形的存在性问题一、已知三个定点,再找一个定点构成平行四边形（平面内有三个点满足）在直角坐标平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形,请写出点M的坐标。

2与x轴的一个交点为A(-1,0），与y轴的正半轴交于点C．1.已知抛物线b-=2+axaxy+⑴直接写出抛物线的对称轴，及抛物线与x轴的另一个交点B的坐标;⑵当点C在以AB为直径的⊙P上时,求抛物线的解析式；⑶坐标平面内是否存在点M，使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形？若存在,请求出点M的坐标；若不存在，请说明理由．二、已知两个定点，再找两个点构成平行四边形①确定两定点连接的线段为一边，则两动点连接的线段应和已知边平行且相等)2.已知抛物线：x x y 22121+-=（1）求抛物线1y 的顶点坐标.（2）将抛物线1y 向右平移2个单位，再向上平移1个单位，得到抛物线2y ，求抛物线2y 的解析式. （3）如下图，抛物线2y 的顶点为P ，x 轴上有一动点M ，在1y 、2y 这两条抛物线上是否存在点N ，使O （原点）、P 、M 、N 四点构成以OP 为一边的平行四边形，若存在，求出N 点的坐标;若不存在，请说明理由.②两定点连接的线段没确定为平行四边形的边时，则这条线段可能为平行四边形得边或对角线3．如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2．（1）求A 、B 两点的坐标及直线AC 的函数表达式；(2）P 是线段AC 上的一个动点，过P 点作y 轴的平行线交抛物线于E 点, 求线段PE 长度的最大值；(3）点G 抛物线上的动点,在x 轴上是否存在点F,使A 、C 、F 、G 这样 的四个点为顶点的四边形是平行四边形？如果存在,求出所有满足条件的F点坐标；如果不存在，请说明理由．4．已知:如图所示，关于x 的抛物线2(0)y ax x c a =++≠与x 轴交于点(20)A -，、点(60)B ，，与y 轴交于点C ．（1）求出此抛物线的解析式，并写出顶点坐标；（2）在抛物线上有一点D,使四边形ABDC为等腰梯形，写出点D的坐标，并求出直线AD的解析式;（3)在(2）中的直线AD交抛物线的对称轴于点M，抛物线上有一动点P，x轴上有一动点Q．是否存在以、、、为顶点的平行四边形？如果存在,请直接写出点Q的坐标；如果不存在,请说明理由．A M P Q练习:1．如图，抛物线经过A(﹣1，0），B（5,0），C（0，）三点．（1）求抛物线的解析式;(2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；(3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标;若不存在，请说明理由．2．如图，抛物线y=ax2+bx+c(a≠0）与y轴交于点C(0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0)，抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．(1）求抛物线的解析式;(2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标；若不存在,请说明理由;（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标．3．已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0）,B(β,0），且=﹣2，（1）求抛物线的解析式．（2）抛物线的对称轴为l,与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N,使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．4．如图，直线y=﹣x+3与x轴交于点C，与y轴交于点B，抛物线y=ax2+x+c经过B、C两点．（1)求抛物线的解析式；（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值？（3）在（2）的结论下,过点E作y轴的平行线交直线BC于点M，连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．5．如图，抛物线与x轴交于A、B两点,与y轴交于点C，且OA=2，OC=3．(1)求抛物线的解析式;(2）作Rt△OBC的高OD，延长OD与抛物线在第一象限内交于点E，求点E的坐标；（3）①在x轴上方的抛物线上，是否存在一点P，使四边形OBEP是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由；②在抛物线的对称轴上，是否存在上点Q，使得△BEQ的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由．。

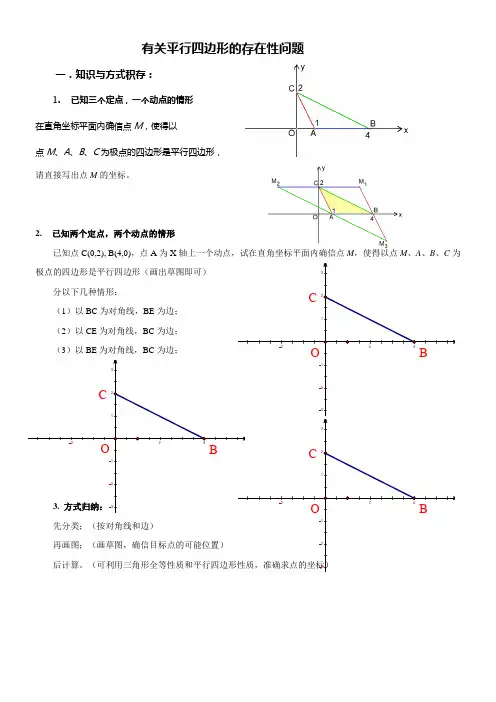
有关平行四边形的存在性问题一．知识与方式积存：1.已知三个定点，一个动点的情形在直角坐标平面内确信点M，使得以点M、A、B、C为极点的四边形是平行四边形，请直接写出点M的坐标。

二．例题解析：如图，抛物线32++=bx ax y 与y 轴交于点C ，与x 轴交于A 、B 两点，31tan =∠OCA ，6=∆ABC S ． （1）求点B 的坐标； （2）求抛物线的解析式及极点坐标；（3）设点E 在x 轴上，点F 在抛物线上，若是A 、C 、E 、F 组成平行四边形，请求出点E 的坐标．巩固练习：1. 已知抛物线322++-=x x y 与x 轴的一个交点为 A(-1,0)，与y 轴的正半轴交于点C ． 问坐标平面内是不是存在点M ，使得以点M 和抛物线上的三点A 、B 、C 为极点的四边形是平行四边形？假设存在，请求出点M 的坐标；假设不存在，请说明理由．2. 假设点P 是x 轴上一点，以P 、A 、D 为极点作平行四边形，该平行四边形的另一极点E 在y 轴上，写出点P的坐标．3．如图，抛物线223y x x =-++与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，极点为D .（1）直接写出（2）连接BC 于点F ，设点P CAB Oyx4. 已知抛物线22y x x a =-+（0a <）与y 轴相交于点A ，极点为M .直线12y x a =-别离与x 轴，y 轴相交于B C ，两点，而且与直线AM 相交于点N .在抛物线22y x x a =-+（0a <）上是不是存在一点P ，使得以P A C N ，，，为极点的四边形是平行四边形？假设存在，求出P 点的坐标；假设不存在，试说明理由.5．如图，已知抛物线)0(2≠++=a c bx ax y 的极点坐标为Q ()1,2-，且与y 轴交于点C ()3,0，与x 轴交于A 、B 两点（点A 在点B 的右边），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD ∥y 轴，交AC 于点D ． (1)求该抛物线的函数关系式；(2)当△ADP 是直角三角形时，求点P 的坐标；(3)在问题(2)的结论下，假设点E 在x 轴上，点F 在抛物线上， 问是不是存在以A 、P 、E 、F 为极点的平行四边形？假设存在， 求点F 的坐标；假设不存在，请说明理由．6. 如图，抛物线21y ax bx =++与x 轴交于两点A （－1，0），B （1，0），与y 轴交于点C ． (1)求抛物线的解析式；（12+-=x y ）(2)过点B 作BD ∥CA 与抛物线交于点D ，求四边形ACBD 的面积；四边形ACBD 的面积S =12AB •OC +12AB •DE 112123422=⨯⨯+⨯⨯= （也可直接求直角梯形ACBD 的面积为4）(3)在x 轴下方的抛物线上是不是存在一点M ，过M 作MN ⊥x 轴于点N ，使以A 、M 、N 为极点的三角形与△BCD 相似？假设存在，那么求出点M 的坐标；假设不存在，请说明理由．。

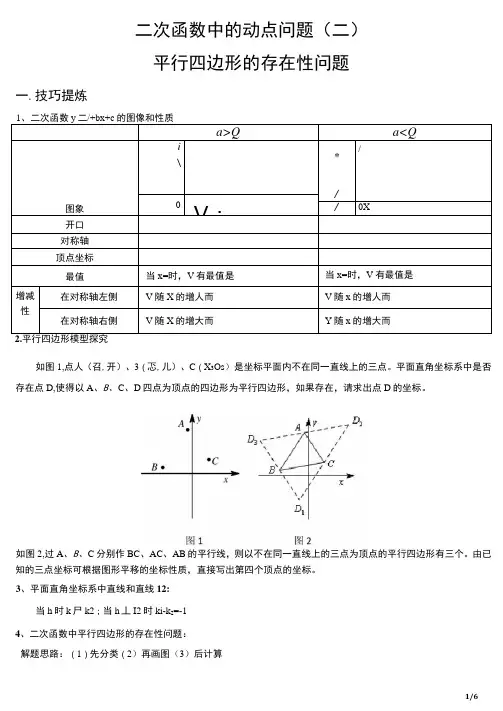
二次函数中的动点问题（二）平行四边形的存在性问题一.技巧提炼如图1,点人（召,开）、3（忑,儿）、C（X3Os）是坐标平面内不在同一直线上的三点。

平面直角坐标系中是否存在点D,使得以A、B、C、D四点为顶点的四边形为平行四边形，如果存在，请求出点D的坐标。

如图2,过A、B、C分别作BC、AC、AB的平行线，则以不在同一直线上的三点为顶点的平行四边形有三个。

由已知的三点坐标可根据图形平移的坐标性质，直接写出第四个顶点的坐标。

3、平面直角坐标系中直线和直线12:当h时k尸k2；当h丄I2时ki-k2=-14、二次函数中平行四边形的存在性问题：解题思路：（1）先分类（2）再画图（3）后计算二、精讲精练1、已知抛物线y=ax-+bx+c与x轴相交于A、E两点（A、B分别在原点的左右两侧），与y轴正半轴相交于C点，且OA：OB：OC=1：3：3,AABC的面积为6,（如图1）（1）求抛物线的解析式：（2）坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由；（3）如图2,在直线BC±方的抛物线上是否存在一动点P,ABCP面枳最大？如果存在，求出最人面积,2、如图，己知抛物线经过A(-2,0),B(・3,3)及原点6顶点为C(1)求抛物线的函数解析式：(2)设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标。

【变式练习】7如图，对称轴为直线x二一的抛物线经过点A(6,0)和B(0,4)・2(1)求抛物线解析式及顶点坐标；(2)设点E(x,y)是抛物线上一动点，且位于第四彖限，四边形0EAF是以0A为对角线的平行四边形, 求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；①当平行四边形OEAF的面积为24时，请判断平行四边形0EAF是否为菱形？②是否存在点E,使平行四边形0EAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由.、方法规律1、平行四边形模型探究如图1，点&（內,开）、3（七,儿）、C（X3，”）是坐标平面内不在同一直线上的三点。

二次函数中的平行四边形存在性问题
例1：在平面直角坐标系中，已知抛物线经过A(-4，0)，B(0，-4)，C(2，0)三点.:(1)求抛物线的解析式；(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S.求S 关于m 的函数关系式，并求出S 的最大值； (3)若点P 是抛物线上的动点，点Q 是直线y=－x 上的动点，判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标.
1、如图1，抛物线322++-=x x y 与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为
D ．
（1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴；（2）连结BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作PF //DE 交抛物线于点F ，设点P 的横坐标为m ．①用含m 的代数式表示线段PF 的长，并求出当m 为何值时，四边形PEDF 为平行四边形？设△BCF 的面积为S ，求S 与m 的函数关系．
例2、已知抛物线322++-=x x y 与x 轴的一个交点为 A(-1,0)，与y 轴的正半轴交于点C ． 问坐标平面内是否存在点M ，使得以点M 和抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形？若存在，请求出点M 的坐标；若不存在，请说明理由．
1、已知抛物线22y x x a =-+（0a <）与y 轴相交于点A ，顶点为M .直线12
y x a =-分别与x 轴，y 轴相交于B C ，两点，并且与直线AM 相交于点N .在抛物线22y x x a =-+（0a <）上是否存在一点P ，使得以P A C N ，，，为顶点的四边形是平行四边形？若存在，求出P 点的坐标；若不存在，试说明理由.。

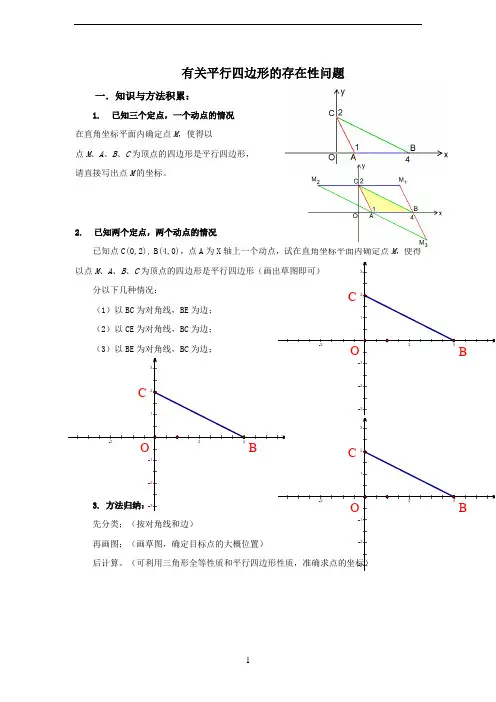
有关平行四边形的存在性问题一．知识与方法积累：1.已知三个定点，一个动点的情况在直角坐标平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形，请直接写出点M的坐标。

二．例题解析：如图，抛物线32++=bxaxy与y轴交于点C，与x轴交于A、B两点，31tan=∠OCA，6=∆ABCS．（1）求点B的坐标；（2）求抛物线的解析式及顶点坐标；（3）设点E在x轴上，点F在抛物线上，如果A、C、E、F构成平行四边形，请求出点E的坐标．巩固练习：1. 已知抛物线322++-=xxy与x轴的一个交点为 A(-1,0)，与y轴的正半轴交于点C．问坐标平面内是否存在点M，使得以点M和抛物线上的三点A、B、C为顶点的四边形是平行四边形若存在，请求出点M的坐标；若不存在，请说明理由．2. 若点P是x轴上一点，以P、A、D为顶点作平行四边形，该平行四边形的另一顶点E在y轴上，写出点P的坐标．CAB Oyx3．如图，抛物线223y x x =-++与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为D .（1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴；（2）连接BCPF DE ∥为平行四边形4. 已知抛物线y =2x =分别与x 轴，y 轴相交于B C ，两点，并且与直线AM 相交于点N .在抛物线22y x x a =-+（0a <）上是否存在一点P ，使得以P A C N ，，，为顶点的四边形是平行四边形若存在，求出P 点的坐标；若不存在，试说明理由.5．如图，已知抛物线)0(2≠++=a c bx ax y 的顶点坐标为Q ()1,2-，且与y 轴交于点C ()3,0，与x 轴交于A 、B 两点（点A 在点B 的右侧），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD ∥y 轴，交AC 于点D ． (1)求该抛物线的函数关系式；(2)当△ADP 是直角三角形时，求点P 的坐标；(3)在问题(2)的结论下，若点E 在x 轴上，点F 在抛物线上， 问是否存在以A 、P 、E 、F 为顶点的平行四边形若存在， 求点F 的坐标；若不存在，请说明理由．6. 如图，抛物线21y ax bx =++与x 轴交于两点A （－1，0），B （1，0），与y 轴交于点C ．(1)求抛物线的解析式；（12+-=x y ）(2)过点B 作BD ∥CA 与抛物线交于点D ，求四边形ACBD 的面积；四边形ACBD 的面积S =12AB •OC +12AB •DE 112123422=⨯⨯+⨯⨯= （也可直接求直角梯形ACBD 的面积为4）(3)在x 轴下方的抛物线上是否存在一点M ，过M 作MN ⊥x 轴于点N ，使以A 、M 、N 为顶点的三角形与△BCD 相似若存在，则求出点M 的坐标；若不存在，请说明理由．。

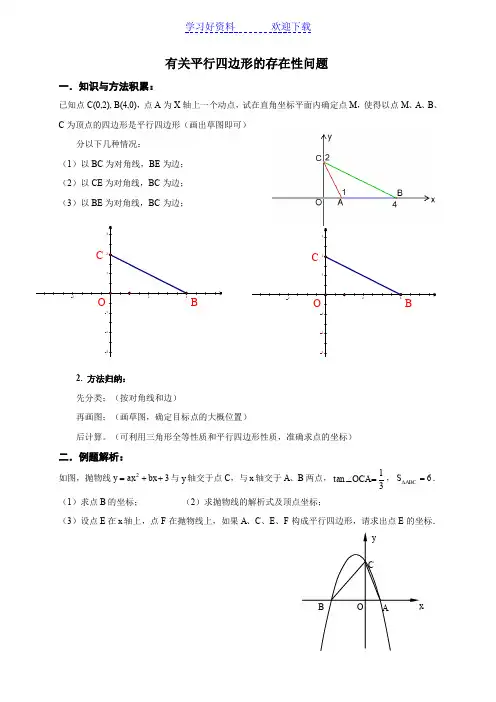
有关平行四边形的存在性问题一．知识与方法积累：已知点C(0,2), B(4,0)，点A 为X 轴上一个动点，试在直角坐标平面内确定点M ，使得以点M 、A 、B 、C 为顶点的四边形是平行四边形（画出草图即可）分以下几种情况：（1）以BC 为对角线，BE 为边；（2）以CE 为对角线，BC 为边； （3）以BE 为对角线，BC 为边；2. 方法归纳：先分类；（按对角线和边）再画图；（画草图，确定目标点的大概位置）后计算。

（可利用三角形全等性质和平行四边形性质，准确求点的坐标）二．例题解析：如图，抛物线32++=bx ax y 与y 轴交于点C ，与x 轴交于A 、B 两点，31tan =∠OCA ，6=∆ABC S ． （1）求点B 的坐标； （2）求抛物线的解析式及顶点坐标；（3）设点E 在x 轴上，点F 在抛物线上，如果A 、C 、E 、F 构成平行四边形，请求出点E 的坐标．321123422468OBC321123422468OBCCABOy x巩固练习：1. 已知抛物线322++-=x x y 与x 轴的一个交点为 A(-1,0)，与y 轴的正半轴交于点C ． 问坐标平面内是否存在点M ，使得以点M 和抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形？若存在，请求出点M 的坐标；若不存在，请说明理由．2. 已知抛物线22y x x a =-+（0a <）与y 轴相交于点A ，顶点为M .直线12y x a =-分别与x 轴，y 轴相交于B C ，两点，并且与直线AM 相交于点N .在抛物线22y x x a =-+（0a <）上是否存在一点P ，使得以P A C N ，，，为顶点的四边形是平行四边形？若存在，求出P 点的坐标；若不存在，试说明理由.3.已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0)，与y 轴的正半轴交于点C ． ⑴直接写出抛物线的对称轴，及抛物线与x 轴的另一个交点B 的坐标； ⑵当点C 在以AB 为直径的⊙P 上时，求抛物线的解析式；⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形？若存在,请求出点M 的坐标；若不存在,请说明理由．4.已知抛物线22y x x a =-+（0a <）与y 轴相交于点A ，顶点为M .直线12y x a =-分别与x 轴，y 轴相交于B C ，两点，并且与直线AM 相交于点N .(1)填空：试用含a 的代数式分别表示点M 与N 的坐标，则()()M N ， ， ， ； (2)如图，将NAC △沿y 轴翻折，若点N 的对应点N ′恰好落在抛物线上，AN ′与x 轴交于点D ，连结CD ，求a 的值和四边形ADCN 的面积；(3)在抛物线22y x x a =-+（0a <）上是否存在一点P ，使得以P A C N ，，，为顶点的四边形是平行四边形？若存在，求出P 点的坐标；若不存在，试说明理由.第（4）题xy BC ODA MN N ′ BN①确定两定点连接的线段为一边，则两动点连接的线段应和已知边平行且相等5.已知，如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点，与x 轴交于A 、B 两点，A 点在B 点左侧。

二次函数存在性问题 专题---------平行四边形存在性姓名：例1：如图，在平面直角坐标系xOy 中，抛物线y=（x ﹣m ）2﹣m 2+m 的顶点为A ，与y 轴的交点为B ，连结AB ，AC ⊥AB ，交y 轴于点C ，延长CA 到点D ，使AD=AC ，连结BD ．作AE ∥x 轴，DE ∥y 轴．（1）当m=2时，求点B 的坐标；（2）求DE 的长？（3）①设点D 的坐标为（x ，y ），求y 关于x 的函数关系式？②过点D 作AB 的平行线，与第（3）①题确定的函数图象的另一个交点为P ，当m 为何值时，以，A ，B ，D ，P 为顶点的四边形是平行四边形？1、已知二次函数c bx x y ++=2，其图像抛物线交x 轴的于点A （1，0）、B （3，0），交y 轴于 点C.直线l 过点C ，且交抛物线于另一点E （点E 不与点A 、B 重合）.(1)求此二次函数关系式；(2)若直线1l 经过抛物线顶点D ，交x 轴于点F ，且1l ∥l ，则以点C 、D 、E 、F 为顶点的四边形能否为平行四边形？若能，求出点E 的坐标；若不能，请说明理由.(3)若过点A 作AG ⊥x 轴，交直线l 于点G ，连OG 、BE ，试证明OG ∥BE.例2：如图，矩形OABC 在平面直角坐标系xOy 中，点A 在x 轴的正半轴上，点C 在y 轴的正半轴上，OA=4，OC=3，若抛物线的顶点在BC 边上，且抛物线经过O ，A 两点，直线AC 交抛物线于点D ．（1）求抛物线的解析式；（2）求点D 的坐标；（3）若点M 在抛物线上，点N 在x 轴上，是否存在以A ，D ，M ，N 为顶点的四边形是平行四边形？若存在，求出点N 的坐标；若不存在，请说明理由．1、如图，抛物线y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，过点A作直线AC⊥x 轴，交直线y=2x于点C；（1）求该抛物线的解析式；（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．:3、如图，抛物线经过A（﹣1，0），B（5，0），C（0，）三点．（1）求抛物线的解析式；（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；（3）点M 为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．。