最小二乘法在经济预测中的应用
- 格式:doc
- 大小:46.00 KB
- 文档页数:11

最小二乘法是一种数学优化技术,它通过最小化误差的平方和来寻找数据的最佳函数匹配。
在许多领域,如线性回归分析、曲线拟合、机器学习、信号处理、控制系统、金融预测和经济建模等,最小二乘法都得到了广泛的应用。
以下是一些最小二乘法的用法举例:1. 线性回归分析线性回归分析是一种统计学方法,用于研究因变量和自变量之间的关系。
最小二乘法可以用于估计线性回归模型的参数,使得预测值和实际观测值之间的残差平方和最小化。
2. 曲线拟合曲线拟合是一种数学方法,用于将一组数据拟合到一个特定的函数模型中。
最小二乘法可以用于估计模型的参数,使得模型预测值和实际观测值之间的残差平方和最小化。
3. 机器学习机器学习是一种人工智能技术,用于让计算机从数据中学习并自动改进其性能。
最小二乘法可以用于训练机器学习模型,例如线性回归模型、逻辑回归模型和支持向量机等。
4. 信号处理信号处理是一种技术,用于对信号进行变换、分析和合成。
最小二乘法可以用于估计信号的参数,例如频率、幅度和相位等,使得信号的预测值和实际观测值之间的残差平方和最小化。
5. 控制系统控制系统是一种技术,用于控制系统的行为并使其达到预期的性能指标。
最小二乘法可以用于估计控制系统的参数,例如传递函数和状态空间模型等,使得控制系统的预测值和实际观测值之间的残差平方和最小化。
6. 金融预测金融预测是一种技术,用于预测金融市场的走势和未来趋势。
最小二乘法可以用于估计金融模型的参数,例如ARIMA模型和神经网络模型等,使得模型的预测值和实际观测值之间的残差平方和最小化。
7. 经济建模经济建模是一种技术,用于建立经济系统的数学模型并对其进行仿真和分析。
最小二乘法可以用于估计经济模型的参数,例如生产函数和需求函数等,使得模型的预测值和实际观测值之间的残差平方和最小化。

最小二乘法在回归分析和趋势预测中的应用最小平方法,又称最小二乘法。
其方法的计算依据是利用算术平均数的数学性质,在我们介绍算术平均数的数学性质时,有两条性质分别是:一、各个变量值与平均数的离差之和等于零,用表达式表示即0)(=-∑x x ;二、各个变量值与平均数的离差平方之和为最小值,用表达式表示为最小值=-∑2)(x x 。
这两条数学性质已证明过,我们把它们应用到回归分析和趋势预测中来。
回归分析和时间序列趋势预测中,主要是为求得回归方程或趋势方程,但在求得方程的参数时,就要用到上面的两条数学性质。
最小平方法的数学依据是实际值(观察值)与理论值(趋势值)的离差平方和为最小。
据此来拟合回归方程或趋势方程。
1、利用最小平方法拟合直线回归方程拟合直线回归方程的主要问题就在于估计待定参数a 和b 之值,而用最小平方法求出的回归直线是原有资料的“最佳”拟合直线。
假设直线回归方程为:bx a y c +=,其中a 是直线的截距,b 是直线的斜率,称回归系数。
a 和b 都是待定参数。
将给定的自变量x 之值代入上述方程中,可求出估计的因变量y 之值。
这个估计值不是一个确定的数值,而是y 许多可能取值的平均数,所以用c y 表示。
当x 取某一个值时,y 有多个可能值。
因此,将给定的x 值代入方程后得出的c y 值,只能看作是一种平均数或期望值。
配合直线方程的具体方法如下:∑=-=最小值2)(c y y Q (1) 用直线方程bx a y c +=代入式(1)得:最小值=--=∑2)(bx a y Q (2) 分别求Q 关于a 和Q 关于b 的偏导,并令它们等于0:⎪⎩⎪⎨⎧=---=∂∂=---=∂∂∑∑0))((20)1)((2x bx a y b Q bx a y a Q整理后得出由下列两个方程式所组成的标准方程组:⎩⎨⎧+=+=∑∑∑∑∑2x b x a xy x b na y (3)根据已知的或样本的相应资料x 、y 值代入式(3),可求出a 和b 两个参数:⎪⎪⎩⎪⎪⎨⎧-=--=∑∑∑∑∑∑∑n x b n y a x x n y x xy n b 22)( (4)只要把a 和b 两个参数代入c y ,就可得到直线回归方程bx a y c +=。

标准最小二乘法标准最小二乘法(Ordinary Least Squares, OLS)是一种常用于回归分析的方法,旨在通过拟合数据来找到最合适的模型。
在本文中,将详细介绍标准最小二乘法的原理、应用和计算步骤。
标准最小二乘法的原理十分简单直观,它通过寻找使得拟合模型与观测数据之间误差的平方和最小的参数估计值。
在回归分析中,我们通常会假设一个线性模型来描述自变量和因变量之间的关系。
标准最小二乘法通过最小化残差的平方和来找到最佳拟合的模型。
残差即观测值与拟合值之间的差异。
在应用标准最小二乘法进行回归分析时,需要先确定一个合适的模型。
通常,我们会选择一个线性模型来描述因变量和自变量之间的关系,然后通过参数估计找到最佳的拟合模型。
这一过程可以通过最小化残差平方和的方法来实现。
在计算步骤上,标准最小二乘法可以分为以下几个关键步骤。
首先,需要确定线性模型的形式,并根据实际情况选择自变量。
其次,通过收集样本数据,计算出相关的变量值。
然后,利用计算出的变量值进行模型参数的估计。
最后,通过计算残差平方和,确定最佳的拟合模型。
标准最小二乘法在实际应用中具有广泛的意义和应用价值。
例如,在经济学中,可以利用标准最小二乘法来估计供求关系和弹性系数。
在工程领域,可以通过标准最小二乘法来建立物理模型并进行预测。
在社会科学中,也可以利用标准最小二乘法来研究变量之间的关系。
总结而言,标准最小二乘法是一种常用的回归分析方法,通过最小化残差平方和来找到最佳的拟合模型。
它的计算步骤简单清晰,适用于各个领域的数据分析和预测。
通过合理应用标准最小二乘法,可以有效地研究自变量和因变量之间的关系,为实际问题提供有力的解决方案。
综上所述,标准最小二乘法是一种重要的分析工具,具有广泛的应用前景。
它不仅可以帮助我们理解数据,还可以通过拟合模型来进行预测和分析。
在实际应用中,我们应当遵循标准最小二乘法的原理和计算步骤,以确保分析结果的准确性和可靠性。
通过深入学习和理解标准最小二乘法,我们能够更好地利用这一工具解决实际问题。


最小二乘法实现公式最小二乘法是一种常用的回归分析方法,用于估计线性模型中的参数。
它通过最小化观测值与预测值之间的误差平方和,来确定最优的参数估计值。
下面将详细介绍最小二乘法的原理和应用。
一、最小二乘法原理最小二乘法的基本思想是,通过找到一条线(或曲线),使得该线与观测数据点之间的误差最小化。
具体来说,对于一个线性模型 y = β0 + β1x + ε,其中 y 是因变量,x 是自变量,β0 和β1 是待估计的参数,ε 是误差项。
最小二乘法的目标是找到最优的参数估计值β0* 和β1*,使得观测值与预测值之间的误差平方和最小化。
为了实现最小二乘法,需要定义一个衡量误差的函数,通常选择误差的平方和作为目标函数。
即最小化目标函数:min Σ(yi - (β0 + β1xi))^2通过对目标函数求导,可以得到参数估计值的解析解。
令目标函数的导数等于零,可以得到以下两个方程:Σyi - nβ0 - β1Σxi = 0Σxiyi - β0Σxi - β1Σxi^2 = 0解这个方程组,可以求得最优的参数估计值β0* 和β1*。
最小二乘法的核心思想就是通过最小化误差平方和来确定最优的参数估计值。
二、最小二乘法的应用最小二乘法广泛应用于各个领域的回归分析中。
下面将介绍最小二乘法在经济学、统计学和工程学中的应用。
1. 经济学中的应用最小二乘法在经济学中被广泛应用于建立经济模型和估计经济参数。
经济学家可以利用最小二乘法来估计需求函数、供给函数和生产函数等。
通过回归分析,经济学家可以研究各种经济变量之间的关系,并对经济现象进行解释和预测。
2. 统计学中的应用最小二乘法是统计学中最常用的参数估计方法之一。
通过最小二乘法,统计学家可以估计线性回归模型中的参数,并进行统计推断。
最小二乘法还可以用于解决多重共线性、异方差性和自相关等统计问题。
3. 工程学中的应用最小二乘法在工程学中有着广泛的应用。
例如,在信号处理中,最小二乘法可以用于信号滤波和信号重构。
最小二乘估计原理最小二乘估计原理是一种常用的参数估计方法,它在统计学和经济学等领域有着广泛的应用。
最小二乘估计原理的核心思想是通过最小化观测值与估计值之间的残差平方和来确定参数的估计值,从而使得模型拟合数据的效果最佳。
在本文中,我们将详细介绍最小二乘估计原理的基本概念、应用场景以及具体的计算方法。
最小二乘估计原理的基本概念。
最小二乘估计原理的基本思想是通过最小化残差平方和来确定参数的估计值。
在线性回归模型中,我们通常假设因变量与自变量之间存在线性关系,即Y = β0 + β1X + ε,其中Y表示因变量,X表示自变量,β0和β1分别表示截距和斜率,ε表示误差项。
最小二乘估计原理要求通过最小化观测值与估计值之间的残差平方和来确定参数的估计值,即使得残差平方和达到最小值时,参数的估计值即为最小二乘估计值。
最小二乘估计原理的应用场景。
最小二乘估计原理广泛应用于线性回归模型的参数估计中。
在实际应用中,我们经常需要根据样本数据来估计模型的参数,从而进行预测或者推断。
最小二乘估计原理可以帮助我们确定最优的参数估计值,使得模型能够最好地拟合观测数据。
除了线性回归模型,最小二乘估计原理还可以应用于其他类型的模型参数估计中,例如非线性模型、多元回归模型等。
最小二乘估计的具体计算方法。
在实际应用中,最小二乘估计的具体计算方法通常包括以下几个步骤,首先,建立模型,确定自变量和因变量之间的关系;其次,利用样本数据来估计模型的参数,即通过最小化残差平方和来确定参数的估计值;最后,进行参数估计的检验,判断参数的估计结果是否显著。
在具体计算过程中,通常需要利用计量经济学中的相关工具和方法,例如OLS(Ordinary Least Squares)估计方法、假设检验、置信区间估计等。
最小二乘估计原理的优缺点。
最小二乘估计原理作为一种常用的参数估计方法,具有以下优点,首先,计算简单,易于理解和应用;其次,具有较好的数学性质和统计性质,例如无偏性、有效性等;最后,适用范围广泛,可以应用于各种类型的模型参数估计中。
最小二乘法和theil-sen趋势估计方法概述说明以及解释1. 引言1.1 概述引言部分将总体介绍本篇文章的研究主题和方法。
本文将探讨最小二乘法和Theil-Sen趋势估计方法,这两种方法旨在通过拟合数据来寻找变量间的关系,并用于预测和估计未来的趋势。
最小二乘法是一种常见且广泛应用的回归分析方法,而Theil-Sen趋势估计方法是一种鲁棒性更强的非参数统计方法。
1.2 文章结构引言部分还需要简要描述整篇文章的结构以供读者参考。
本文包含以下几个主要部分:引言、最小二乘法、Theil-Sen趋势估计方法、对比与对比分析、结论与展望。
每个部分将详细说明相关概念、原理及其在实际应用中的特点。
1.3 目的引言部分还需明确指出本文的目的。
本文旨在比较和对比最小二乘法和Theil-Sen趋势估计方法,评估它们在不同场景下的优缺点,并为读者提供选择适当方法进行数据拟合和趋势预测的依据。
此外,我们也会展望未来这两种方法的改进和应用领域扩展的可能性。
以上为“1. 引言”部分的详细清晰撰写内容。
2. 最小二乘法:2.1 原理介绍:最小二乘法是一种常用的回归分析方法,用于寻找一个函数(通常是线性函数)来逼近已知数据点的集合。
其基本原理是通过最小化实际观测值与模型预测值之间的残差平方和,寻找到使得残差最小化的系数,并将其作为估计值。
利用最小二乘法可以得到拟合直线、曲线或者更复杂的函数来描述数据点之间的关系。
2.2 应用场景:最小二乘法广泛应用于各种领域和行业,包括经济学、社会科学、物理学等。
例如,在经济学中,最小二乘法可以用于研究变量之间的关系以及预测未来趋势。
在工程领域,它可以用于建立模型并进行参数估计。
2.3 优缺点分析:最小二乘法具有以下优点:- 算法简单易行:只需要对数据进行简单处理即可求解出最佳拟合曲线。
- 表示能力强:可以适应不同类型函数的拟合。
- 结果一致性较好:针对相同数据集,得到的结果通常是一致的。
然而,最小二乘法也存在一些缺点:- 对异常值敏感:在数据集中存在离群值时,会对拟合曲线产生较大影响。
一、最小二乘法最小二乘法是一种常用的数据拟合方法,它通过最小化实际观测值与模型预测值之间的差异来寻找最佳拟合曲线或平面。
在统计学和经济学中,最小二乘法常常用于回归分析,计算出拟合曲线的斜率和截距,从而评估自变量对因变量的影响。
Stata软件提供了一系列的最小二乘法命令,包括regress、ivregress、qreg等,用户可以根据具体的需求选择合适的命令进行数据拟合和参数估计。
在Stata中,使用最小二乘法进行数据拟合的命令有:1. regress:该命令用于执行普通最小二乘回归分析,对于单变量或多变量回归分析都适用。
2. ivregress:该命令用于执行被认为与误差项相关的内生变量的最小二乘估计。
3. qreg:该命令用于进行分位数回归分析,对于分布式数据的回归分析非常有用。
通过这些命令,用户可以方便地进行数据拟合和参数估计,快速得到符合最小二乘法原理的拟合结果,从而进行进一步的统计分析和推断。
二、GMM广义矩估计(GMM)是一种参数估计方法,它通过最大化或最小化一组样本矩来估计模型参数。
在经济学、金融学和计量经济学等领域,GMM广泛应用于参数估计和模型拟合。
Stata软件提供了一系列的GMM命令,用户可以根据具体的需求使用不同的命令进行模型估计和拟合。
在Stata中,使用GMM进行参数估计和模型拟合的命令有:1. ivreg:该命令用于执行广义矩估计的内生变量回归分析。
2. gmm:该命令用于执行广义矩估计的一般模型估计。
用户可以根据具体的模型结构和需求使用该命令进行参数估计和模型拟合。
通过这些命令,用户可以方便地进行广义矩估计的参数估计和模型拟合,得到符合GMM原理的拟合结果,从而进行进一步的统计分析和推断。
三、极大似然估计极大似然估计是一种常用的参数估计方法,它通过寻找最大化给定数据样本的概率函数的参数值来估计模型的未知参数。
在统计学、经济学和金融学等领域,极大似然估计被广泛应用于模型的参数估计和拟合。
最小二乘法在回归分析和趋势预测中的应用最小平方法,又称最小二乘法。
其方法的计算依据是利用算术平均数的数学性质,在我们介绍算术平均数的数学性质时,有两条性质分别是:一、各个变量值与平均数的离差之和等于零,用表达式表示即0)(=-∑x x ;二、各个变量值与平均数的离差平方之和为最小值,用表达式表示为最小值=-∑2)(x x 。
这两条数学性质已证明过,我们把它们应用到回归分析和趋势预测中来。
回归分析和时间序列趋势预测中,主要是为求得回归方程或趋势方程,但在求得方程的参数时,就要用到上面的两条数学性质。
最小平方法的数学依据是实际值(观察值)与理论值(趋势值)的离差平方和为最小。
据此来拟合回归方程或趋势方程。
1、利用最小平方法拟合直线回归方程拟合直线回归方程的主要问题就在于估计待定参数a 和b 之值,而用最小平方法求出的回归直线是原有资料的“最佳”拟合直线。
假设直线回归方程为:bx a y c +=,其中a 是直线的截距,b 是直线的斜率,称回归系数。
a 和b 都是待定参数。
将给定的自变量x 之值代入上述方程中,可求出估计的因变量y 之值。
这个估计值不是一个确定的数值,而是y 许多可能取值的平均数,所以用c y 表示。
当x 取某一个值时,y 有多个可能值。
因此,将给定的x 值代入方程后得出的c y 值,只能看作是一种平均数或期望值。
配合直线方程的具体方法如下:∑=-=最小值2)(c y y Q (1) 用直线方程bx a y c +=代入式(1)得:最小值=--=∑2)(bx a y Q (2) 分别求Q 关于a 和Q 关于b 的偏导,并令它们等于0: 整理后得出由下列两个方程式所组成的标准方程组:⎩⎨⎧+=+=∑∑∑∑∑2x b x a xy x b na y (3)根据已知的或样本的相应资料x 、y 值代入式(3),可求出a 和b 两个参数:⎪⎪⎩⎪⎪⎨⎧-=--=∑∑∑∑∑∑∑n x b n y a x x n y x xy n b 22)( (4)只要把a 和b 两个参数代入c y ,就可得到直线回归方程bx a y c +=。
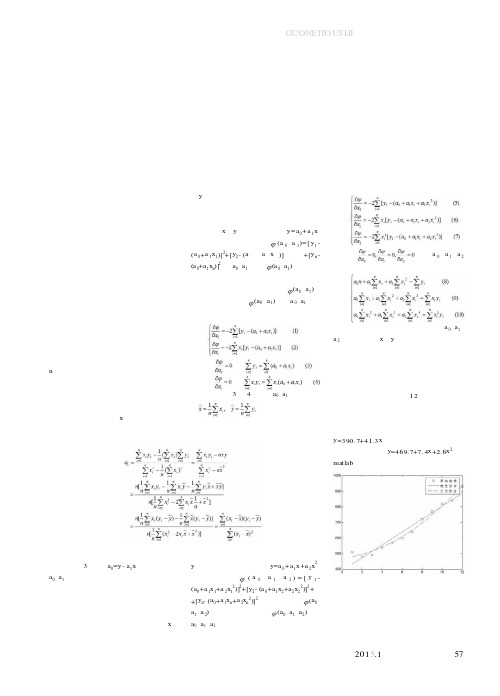
---------------------------------------------------------------最新资料推荐------------------------------------------------------ 最小二乘法在经济预测中的应用最小二乘法在经济预测中的应用王超(绍兴文理学院数学系,浙江绍兴 312019)摘要:作为经济预测中的一种方法,本文介绍了最小二乘法的基本原理,利用最小二乘法建立了线性回归预测模型,同时对相关系数和标准偏差进行检验.最后给出了利用最小二乘法进行经济预测的实例. 关键词:最小二乘法;线性回归;产品生产预测一引言绍兴的经济较为发达,它和宁波、温州三地区的经济位与浙江省前几位,乃致在全国,在长三角开发区中所占的经济地位都很重要. 以绍兴县为例,该县是全国经济百强县之一,全县大都以染料、纺织和布匹等生产加工为主. 笔者了解到支撑绍兴县经济支柱的大部分是以生产加工上述产品的中小企业甚至家庭型企业. 由于他们规模不是很大,因此相应的各技术部门没有很好的配备,所以进行生产管理的方式没有像大型企业那样规范,他们产品的年产量往往根据企业主近几年摸爬滚打中积累起来对市场的判断来制订的,而没有进行科学的经济预测,这常常导致大量产品销售不够或大量产品积压在家,给企业带来严重影响. 经济预测是进行经济决策活动的一个重要组成部分. 在实际经济活动中,预测的结果可以揭示经济现象在未来时期发展变化的情况和发现经济发展过1 / 11程中存在的问题,从而为进行决策、制订计划、提高经济管理水平以及获取较好的经济效益提供了科学依据. 运用定量预测模型进行预测的方法有很多,依据笔者对许多家庭型企业的了解及对企业主知识层次的分析,本文介绍的最小二乘法在经济预测中的应用方法简单明了,比较适合这些企业在进行预测产品产量时参考, 从而能够避免盲目的生产和经营,尽可能地为企业获得最大利润. 二最小二乘法最小二乘法是由实验或调查的数据,建立线性型公式的一种常用方法. 在建立线性型公式中,虽然有很多种不同的方法来求样本回归函数(即,真实总体回归函数的估计值),但是,在回归分析中最广泛应用的方法是最小二乘法. 如果变量yx和有精确的线性关系比如说,那么即观测值与回归值是相等的. 事实上现实世界中的诸多变量的关系未必都是如此,由于受诸多随机因数的干扰使得物与物之间没有那种很明确的对应关系. 比如说人的身高和体重就是一个对应,我们都知道长的高的人不一定就重,同理长的矮的人也不一定就轻,但身高和体重的确存在着一定的关系,而这种关系并非是所能确定的. 那么我们要寻求身高和体重之间的关系就需要通过数学的方法. 首先调查统计得出数据;其次把数据描绘出来;然后拟合一条跟已有的图象最接近的曲线,这样就可以相对地将身高和体重之间的关系表示出来. 在处理类似的事情中常常用到最小二乘法. 所谓最小二乘法就是:选择参数10,bb,使得全部观测的残差平方和最小. 用数学公式---------------------------------------------------------------最新资料推荐------------------------------------------------------3 / 11表示为:为了说明这个方法, 先解释一下最小二乘原理. (一元线性回归方程) 由于总体回归方程不能进行参数估计, 我们只能对样本回归函数来估计即:从(1.1) 公式可以看出:残差ie 是iY 的真实值与估计值之差, 估计总体回归函数最优方法是, 选择10, BB 的估计量10,bb , 使得残差ie 尽可能的小. 总之, 最小二乘原理就是选择样本回归函数使得所有 Y 的估计值与真实值差的平方和为最小, 这种确定10,bb 的方法叫做最小二乘法.在经济关系中, 往往某一指标与多个因素有关, 如果这种关系具备一定的线性相关性, 就可以用多元回归分析来处理, 假设由观测得到一组数据:),...,,(),...,,...,,(),,...,,(212222111211nmnnmmxxxxxxxxx 1y 2y , , ny 令向量分别为:),...,( ),...,,(),...,,(),...,(2, 121222122121,111nnmmmmnnyyyYxxxXxxxXxxxX如果向量组mXXX,...,,21与 Y 存在线性关系,得到 n 元线性预测公式(1.2)其矩阵形式为:(1.3)其中maaa,...,,10为待定常数,亦称回归系数. 如何来确定maaa,...,,10的值呢?将每组观测值代入(1.3)就得到:特别地时(1.4)与iy 间存在差异.记我们选择这样的maaa,...,,10使每个偏差都尽量小,因为偏差()有正有负,所以偏差的代数和并不能反映总体偏差的大小,而数学上处理起来也比较繁杂,所以通常采用使偏差平方和为最小. 即最小(1.5)显然,偏差平方和随maaa,...,,10的变化而取不同的值,可把 S 视为maaa,...,,10的多元函数,并求极值得:---------------------------------------------------------------最新资料推荐------------------------------------------------------5 / 11整理得:mimiiinininnniiimmiiyxxaxxaxxaxayxxxaxxaxaxayxaxaxa1111122211011111121221111011112211.........(1.6) 将上述 m+1 个方程式联立起来就maaa,...,,10求解, 则得到公式(1.5) 的待定系数值, 从而确定了多元线性预测公式. 特别地当时,10,aa 的估计公式为:0) (1.7) 三相关系数与标准偏差 1 相关系数 R 以两个变量的情况为例,因为只要任意给定两个变量yx,的一组数据, 都可以经过计算给出一个经验公式, 这个公式在多大程度上反映了yx,的关系呢? 因为只要通过最小二乘法采取强拟合我们同样可以把一组毫无线性关系的数据表成线性关系,但这条直线并不能很好地反映了变量yx和的实际关系,缺乏应用价值,例如:012345678910111213141513579111315原始散点图强拟合后散点图为此我们一方面要建立从经验上认为有意义的方程,另一方面我们必须用数学方法进行拟合效果和显著性相关检验. 其公式如下:我们称 R=yyxxxyLLL为yx和的相关系数,其中:由上可推算:yyLRS)1由,有,所以,R 越接近 1, S 越接近 0,yx,的线性关系越好. (1)当0, 时,即ie =0,称yx,完全线性关系. (2)当 0,时。
说明yx,无关,即不存在线性关系. (3)当时,可选定相关系数的显著性水平,按的值查相关系数显著性检验表求出临界值(4)当时,说明ix 的值的变化对iy 的值的变化影响很大,yx,存在强相关关系. (5)当时,所求相关关系是无效的,即经验公式是无意义的. 2 标准偏差2其中:---------------------------------------------------------------最新资料推荐------------------------------------------------------7 / 11xyS-------标准偏差 iy --------实例值--------预测值 n --------数据点个数四 预测实例 经验公式是平面上统计点的分布呈线性时的表示形式, 同时它也是最小 二乘理论的形之根本 , 即无论是线性的还是非线性的最后都是要化为这种形式.下面我 们就散点图呈曲线的情况进行预测. 例:对 纺织品销售额的拟合.我们选取销售额为因变量, 单位为万元, 拟合销售额关于时间 x 的趋势曲线. 以 1991 年为基准年, 取值 x =1, 2019 年 x =11, 19912019 年的数据如表一. 表一 年份 x 1991 1992 1993 1994199519961997 1998 1999 20192019 y 19.8 25.6 40.0 49.0 68.0 92.0 112.0138.0182.0 238.0432.0作出表一所给数据的分布图:销售额趋势图0199150100150201950300350销售额40045019931995199719992019年份年份 由散布图可以看出统计点是非线性的, 它大致呈指数形分布. 我们就取经验公式(1.8) 来拟合这条曲线. 这个经验公式所反映的点的排列是非线性的, 我们可以通过取对数将其转化为线性函数 从而运用最小二乘法确定这个线性函数. 即:其中 进而计算的值.取;iy 为各年的销售额;,根据具体数据代入得到如下的表格 . 表二年份2.986 1992 2 25.6 43.243 6.486 1993 3 40.0 9 3.689 11.067 1994 4 49.0 16 3.892 15.568 1995 5 68.0 254.220 21.10 1996 6 92.0 36 4.522 27.132 1997 7 112.0 49 4.718 33.026 1998 8 138.0 64 4.927 39.416 1999 9 182.0 815.204 46.836 2019 10 238.0 100 5.472 54.72 2019 11 432.0 121 6.608 66.748 合计 66 1396.4 506 48.941 325.085 得出:即:查对数表得,将代入(1.8)式中,因此得到了所求的经验公式为:(1.9)下面计算相应系数进行显著性检查:,那么查看关系表(按)---------------------------------------------------------------最新资料推荐------------------------------------------------------9 / 11 得到回归临界值, 因为751. , 说明yx,间存在强相关关系, 可以按公式:进行外推预测, 预测该企业 2019和 2003 年的销售额为:(万元)9044万元)以上是根据散点分布趋势选取曲线来拟合得出的结果, 那么如果我们强行用线性关系即来拟合曲线, 会得出怎样的结果呢? 同样根据数据表 年份 时间序号ix 销售额(万元)iyiiyx 2ix2iy1991 1 19.8 19.8 1 392.04 1992 2 25.6 51.2 4 655.36 1993 3 40.0120 9 1600 1994 4 49.0 196 16 2401 1995 5 68.0 340 25 4624 19966 92.0 552 36 8464 1997 7 112.0 784 49 12544 1998 8 138.0 110464 19044 1999 9 182.0 1638 81 33124 2019 10 238.0 2380 100566442019 11 432.0 4752 121186644 合计 66 1396.4 11937506326116.4得出:得出:因而:( 2.0) 相关系数 879. 08 .14884911查看关系表(按) 得到回归临界值,说明我们可以按公式来进行趋势预测,得出:万元)万元)我们把两组数据比较一下:(万元)9044万元).629(3277.4731万元)万元)显然第二种方法的结果误差太大,这是由于没有考虑散点图分布发展的趋势,强行采用线性拟合的结果. 由此可见. 某产品在一个时期内产量比较稳定,就可用最小二乘法进行趋势预测,但选用曲线来拟合散点时必须依据散点的趋势正确选择曲线,否则有可能出现类似本文的情况即,两条曲线的显著性系数都符合要求都可以用来预测,但其中的一条由于没有分析散点的发展趋势以致于产生的误差太大. 所以企业在日常生产管理中预测方法的科学性,将很大程度上决定企业的利润,从而给经营者制定或调整计划提供了理论依据. Application in Economic Forecasting of Least Square Method Wang Chao Abstract: As a method in economic prediction ,the least square method has been introduced in this paper. We setup the linear regression model with the least square method under usual and special conditions.we also test the coefficientof correlation and standard deviation at the same time .Finally ,we give two examples on economic prediction---------------------------------------------------------------最新资料推荐------------------------------------------------------with the least square method . Key Words: least square method ; linear regression ; production predicting致谢本文写作过程是在丁春梅老师的指导下完成.丁老师不仅提供了参考资料和数据资料,而且还提出了宝贵的修改意见,在此致以衷心的感谢.同时感谢大学四年里所有给予传道授业和帮助的老师们. 参考文献 1 韩於羹,应用数理统计,北京航空航天出版社, 157-191 2 徐天群、董亚娟等,应用数理统计学习指导,武汉大学出版社, 156-170 3 方开泰、全辉等,实用回归分析,科学出版社, 20-94, 141-160 4 岳苓水、赵宝贵,最小二乘法在商品销售预测中的应用,地质技术经济管理, 1997.1 57-60 5 杜国毅,最小二乘法在经济预测中的应用,内蒙古统计, 2019.6 53-5411 / 11。