Eviews做单位根检验和格兰杰因果分析

居民消费物价指数、消费者信心指数的相关数据，利用EVIEWS软件，将这几个指标数据进行相关分析。

特别在这里说明的是，因为同时参与了学校的本科生科研赞助---关于CCI （消费者信心指数）的一个项目，因此本人接下来的几个实验都将以CCI及相关影响指标为数据目标，研究CCI与其他因素间的关系。

本实验，则首先进行相关指标的稳定性检验。

【实验过程】（实验步骤、记录、数据、分析）本实验首先将通过多种方法对我国CCI序列进行平稳性分析：首先导入数据到eviews中,建立序列取名为CCI：然后我们首先通过折线图来直接观察其走势，如下图：从下图我们容易看到：CCI曲线基本是围绕100的轴线上下波动的，但是相比于白噪声序列，其波动幅度明显较大。

可以看到08年11月以前，其波动一直是在轴线以下，而在08年11月以后，数据都明显高于100。

联系当时的实事背景，我们不难解释这一点：2008年11月，正是国家公布四万亿投资的时候，而这之前，由于全球金融危机以及股市大跌的影响，我国居民的消费者信心指数都是较低的；国家的四万亿政策犹如一剂强心剂，立刻使得CCI有了直线的上升，一下子提高了消费者的信心。

为了判别序列是否稳定，我们绘制CCI序列的自相关图，如下：由每个Q统计量的伴随概率可以知道：都是拒绝原假设的，即存在某个K，使得滞后K期的自相关系数显著非零，即拒绝原数列是白噪声序列。

随后对其进行ADF检验：我们首先对序列本身进行单位根检验,分别采用带常数项，线性趋势，和无等三种情况进行检验。

可以从下图看到检验结果对应的p值均显著大于0.05,因此接受原假设,存在单位跟,即CCI序列本身是不平稳的.带常数项线性趋势无因此,考虑对其一阶差分进行单位根检验:可以看到,其一阶差分的单位根检验结果对应的p值显著小于0.01,拒绝存在单位根的原假设，因此我们可以得出结论:CCI的一阶差分序列是平稳的.然后我们通过PP检验来检验序列的平稳性：我们分别采用带常数项，线性趋势，和无等三种情况进行检验。

Eviews基本操作指引：1、ADF检验双击序列——打开序列数据窗口——View——Unit Root Test ——单位根检验对话框（1 st difference ，即检验△X ； intercept：包含截距项； trend：包含趋势项）临界值判断：如果ADF检验值小于某一显着性水平下的临界值，则序列在此显着性水平下平稳。

2、根据SIC和AC值确定VAR的滞后期单位根检验操作的输出结果中3、建立VAR模型在workfile里——Quick——Estimate VAR…——对话窗缺省的是非约束VAR，另一选择是向量误差修正模型。

给出内生变量的滞后期间。

给出用于运算的样本范围。

Endogenous要求给出VAR模型中所包括的内生变量。

Exogenous要求给出外生变量（一般包含常数项）。

结果显示中，回归系数下第一个括号中的为标准差，第二个括号中的为t值。

4、脉冲响应分析（Response of * to * Innovations）/ 方差分解（Variance Decornposition）在进行脉冲响应函数诊断之前，需要先检验VAR模型的平稳性，用AR根图(Inverse Roots of AR Characteristic polunomial)进行检验。

AR根图中，如果点都落在单位圆里，才可以做脉冲分析～如果模型不平稳，则要重新修改变量，去掉不显着变量。

VAR模型估计结果窗口中——View——impulse response——table5、协整关系检验前提条件：序列同阶单整打开序列组数据窗口——View——Cointegration Test…——6、误差修正模型Quick——Estimate VAR…——对话窗——选择VEC——相比较VAR的设置中要多填入误差修正项个数（Number of CE’s），且此时的外生变量设置中不需要再另外设置常数项。

——OK7、格兰杰因果检验前提条件：序列间存在协整关系Eviews可以直接给出两个变量间的双向格兰杰因果检验结果。

EVIEWS各种检验（一）、ADF是单位根检验，第一列数据y做ADF检验，结果如下Null Hypothesis:Y has a unit rootExogenous:Constant,Linear Trend外因的Lag Length:0(Automatic based on SIC,MAXLAG=10)t-Statistic Prob.*Augmented Dickey-Fuller test statistic-3.8200380.0213Test critical values:1%level-4.0987415%level-3.47727510%level-3.166190在1%水平上拒绝原假设，序列y存在单位根，为不平稳序列。

但在5%、10%水平上均接受原假设，认为y平稳。

对y进行一阶差分，差分后进行ADF检验：Null Hypothesis:Y has a unit rootExogenous:NoneLag Length:0(Automatic based on SIC,MAXLAG=10)t-Statistic Prob.* Augmented Dickey-Fuller test statistic-9.3282450.0000Test critical values:1%level-2.5999345%level-1.94574510%level-1.613633可见，在各水平上y都是平稳的。

因此，可以把原序列y看做一阶单整。

第二列xADF检验如下：Null Hypothesis:X has a unit rootExogenous:Constant,Linear TrendLag Length:0(Automatic based on SIC,MAXLAG=10)t-Statistic Prob.* Augmented Dickey-Fuller test statistic-3.2167370.0898Test critical values:1%level-4.0987415%level-3.47727510%level-3.166190在1%、5%水平上拒绝原假设，序列x存在单位根，为不平稳序列。

Eviews格兰杰因果关系检验结果说明一、经济变量之间的因果性问题计量经济模型的建立过程，本质上是用回归分析工具处理一个经济变量对其他经济变量的依存性问题，但这并不是暗示这个经济变量与其他经济变量间必然存在着因果关系。

由于没有因果关系的变量之间常常有很好的回归拟合，把回归模型的解释变量与被解释变量倒过来也能够拟合得很好，因此回归分析本身不能检验因果关系的存在性，也无法识别因果关系的方向。

假设两个变量，比如国内生产总值GDP和广义货币供给量M，各自都有滞后的分量GDP （-1），GDP（-2）…，M（-1），M（-2），…，显然这两个变量都存在着相互影响的关系。

但现在的问题是：究竟是M引起GDP的变化，还是GDP引起M的变化，或者两者间相互影响都存在反馈，即M引起GDP的变化，同时GDP也引起M的变化。

这些问题的实质是在两个变量间存在时间上的先后关系时，是否能够从统计意义上检验出因果性的方向，即在统计上确定GDP是M的因，还是M是GDP的因，或者M和GDP互为因果。

因果关系研究的有趣例子是回答“先有鸡还是先有蛋”的问题。

1988年有两位学者Walter N. Thurman和Mark E. Fisher用美国1930——1983年鸡蛋产量（EGGS）和鸡的产量（CHICKENS）的年度数据，对此问题进行了统计研究。

他们运用格兰杰的方法检验鸡和蛋之间的因果关系，结果发现，鸡生蛋的假设被拒绝，而蛋生鸡的假设成立，因此，蛋为因，鸡为果，也就是先有蛋。

他们并建议作其他诸如“谁笑在最后谁笑得最好”、“骄傲是失败之母”之类的格兰杰因果检验。

二、格兰杰因果关系检验经济学家开拓了一种可以用来分析变量之间的因果的办法，即格兰杰因果关系检验。

该检验方法为2003年诺贝尔经济学奖得主克莱夫·格兰杰（Clive W. J. Granger）所开创，用于分析经济变量之间的因果关系。

他给因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。

以1978~2006年间实际可支配收入（X）和居民实际消费总支出(Y)之间的因果关系为例，做格兰杰检验
1.点击E-view主画面顶部按钮File/New/Workfile，如下图
弹出下图
2.在上图中的Workfile frequency中选择Annual，并输入Start date：1978 和End date：
2006，点击OK，如下图所示
3.再点击主画面中Objects/New Object，弹出如下窗口
4.选择Group，并在Name for Object框输入你要定义的名字如g1,得到下图
5.点击obs右边的单元格，此时该单元格下方所在列会变蓝，如图
在对话框中输入变量名称X,Y及其变量值
6.点击主页面Quick/Group Statistics/Granger Causality Test,得到下图
输入y x,点击Ok，得到下图，
将2改为1点击OK得到下图
武汉理工大学杨超上传。

Eviews做单位根检验和格兰杰因果分析一，首先我根据ADF检验结果，来说明这两组数据对数情况下是否是同阶单整的（同阶单整即说明二者是协整的，这是一种协整检验的方法），我对你的两组数据分别作了单位根检验，结果如下：1.LNFDI水平下的ADF结果：Null Hypothesis: LNFDI has a unit rootExogenous: ConstantLag Length: 2 (Automatic based on AIC, MAXLAG=3) Augmented Dickey-Fuller test statistict-Statistic Prob.*-1.45226403166189 0.526994561264069Test critical values:1% level -4.004424924017175% level -3.0988964053233710% level -2.69043949557234*MacKinnon (1996) one-sided p-values.Warning: Probabilities and critical values calculated for 20observations and may not be accurate for a sample size of 14从上面的t-Statistic对应的值可以看到，-1.45226403166189大于下面所有的临界值，因此LNFDI在水平情况下是非平稳的。

然后我对该数据作了二阶，再进行ADF检验结果如下：t-Statistic Prob.*- 2.8606168858628 0.0770552989049772Test critical values:1% level -4.057909684396635% level -3.1199095651240810% level -2.70110325490427看到t-Statistic的值小于10% level下的-2.70110325490427，因此可以认为它在二阶时，有90%的可能性，是平稳的。

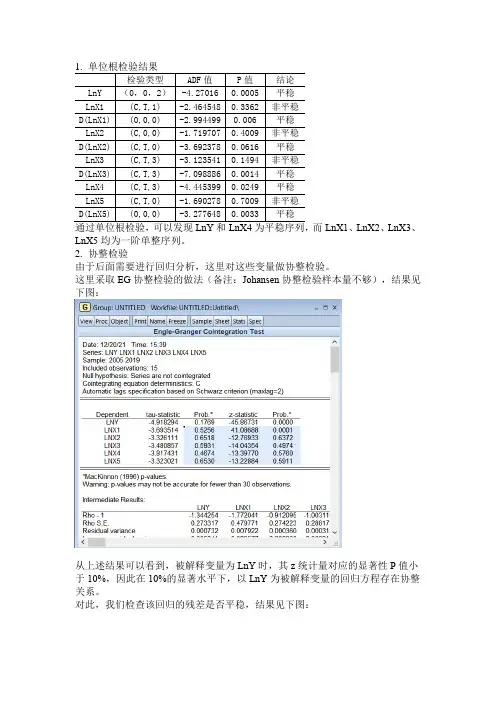
1.单位根检验结果检验类型ADF值P值结论LnY （0，0，2）-4.27016 0.0005 平稳LnX1 (C,T,1) -2.464548 0.3362 非平稳D(LnX1) (0,0,0) -2.994499 0.006 平稳LnX2 (C,0,0) -1.719707 0.4009 非平稳D(LnX2) (C,T,0) -3.692378 0.0616 平稳LnX3 (C,T,3) -3.123541 0.1494 非平稳D(LnX3) (C,T,3) -7.098886 0.0014 平稳LnX4 (C,T,3) -4.445399 0.0249 平稳LnX5 (C,T,0) -1.690278 0.7009 非平稳D(LnX5) (0,0,0) -3.277648 0.0033 平稳通过单位根检验，可以发现LnY和LnX4为平稳序列，而LnX1、LnX2、LnX3、LnX5均为一阶单整序列。

2.协整检验由于后面需要进行回归分析，这里对这些变量做协整检验。

这里采取EG协整检验的做法（备注：Johansen协整检验样本量不够），结果见下图：从上述结果可以看到，被解释变量为LnY时，其z统计量对应的显著性P值小于10%，因此在10%的显著水平下，以LnY为被解释变量的回归方程存在协整关系。

对此，我们检查该回归的残差是否平稳，结果见下图：由残差的单位根检验结果可以看出，此时残差为平稳序列，即该回归存在协整关系。

3.格兰杰因果关系检验由前面的协整检验知LnY与解释变量存在长期的均衡关系，在此基础上，我们对其进行格兰杰因果关系检验。

从上图可以看出LnX1和LnX5不是LnY的格兰杰原因，而LnX2、LnX3、LnX4均是LnY的格兰杰原因，因此我们将建立以LnY为被解释变量，以LnX2、LnX3、LnX4为解释变量的回归。

4.回归结果首先对LnY与LnX2、LnX3、LnX4做协整检验，结果如下：从结果可以看出被解释变量为LnY时，其tau统计量对应的显著性P值小于10%，因此在10%的显著水平下，以LnY为被解释变量的回归存在协整关系。

eviews格兰杰因果关系检验步骤嘿，朋友们！今天咱就来讲讲 eviews 格兰杰因果关系检验的那些步骤。

这可真是个有意思的事儿呢！你想想看，就好像我们要去探索一个神秘的领域，得一步一步稳稳当当走过去。

首先呢，咱得把数据准备好，就像战士上战场得把武器弹药准备齐全一样。

数据可得靠谱啊，不能有啥马虎的。

然后呢，打开 eviews 这个神奇的工具。

嘿，这就像是打开了一扇通往神秘世界的大门。

在里面，我们要找到那个专门做格兰杰因果关系检验的地方。

接着，把我们准备好的数据放进去，就像给机器喂粮食一样。

这时候可别着急，得慢慢来，要确保数据都乖乖进去了，没有乱跑。

之后呢，就是设置一些参数啦。

这就好比给这个检验过程定个规矩，告诉它咱要怎么个检验法。

可不能乱了套呀！再然后，就等着它出结果啦。

这过程就像等待一场比赛的结果一样，心里有点小紧张呢。

等啊等，终于结果出来了。

出来结果后可别急着高兴或者沮丧，得仔细看看，分析分析。

这就像拿到了一份考试成绩单，得看看自己哪儿做得好，哪儿还需要改进。

你说这格兰杰因果关系检验是不是挺有趣的？就像在一个大迷宫里找线索一样。

咱得细心，得耐心，才能找到我们想要的答案。

要是不按照这些步骤来，那可就像没头苍蝇一样乱撞啦，能得出啥好结果呢？所以啊，大家可得记住这些步骤，一步一步来。

在这个过程中，咱可能会遇到一些小麻烦，小挫折，但别怕呀！就像爬山一样，总会有难走的地方，但只要坚持，就能爬到山顶，看到美丽的风景。

总之呢，eviews 格兰杰因果关系检验步骤虽然有点多，但只要咱认真对待，肯定能搞明白的。

大家加油哦！别嫌麻烦，这可是探索知识的乐趣所在呀！。

Eviews做单位根检验和格兰杰因果分析一，首先我根据ADF检验结果，来说明这两组数据对数情况下是否是同阶单整的（同阶单整即说明二者是协整的，这是一种协整检验的方法），我对你的两组数据分别作了单位根检验，结果如下：1.LNFDI水平下的ADF结果：Null Hypothesis: LNFDI has a unit rootExogenous: ConstantLag Length: 2 (Automatic based on AIC, MAXLAG=3 Augmented Dickey-Fuller test statistict-Statistic Prob.*-1.45226403166189 0.526994561264069Test critical values:1% level -4.004424924017175% level -3.0988964053233710% level -2.69043949557234*MacKinnon (1996 one-sided p-values.Warning: Probabilities and critical values calculated for 20observations and may not be accurate for a sample size of 14从上面的t-Statistic对应的值可以看到， -1.45226403166189大于下面所有的临界值，因此LNFDI在水平情况下是非平稳的。

然后我对该数据作了二阶，再进行ADF检验结果如下：t-Statistic Prob.*- 2.8606168858628 0.0770552989049772Test critical values:1% level -4.057909684396635% level -3.1199095651240810% level -2.70110325490427看到t-Statistic的值小于10% level下的-2.70110325490427，因此可以认为它在二阶时，有90%的可能性，是平稳的。

金融论文计量教学根据我以往写论文所用到的检验方法，特别总结出这篇《如何用EViews计量软件帮金融类论文建模分析》，其中有基本操作、单位根检验、VAR模型估计、格兰杰因果关系检验、脉冲响应分析以及方差分解。

希望能够帮助有这方面需求的同学们排难解疑。

关键词：单位根 VAR Granger 脉冲响应方差分解目录一、录入数据写金融类论文，常常会用到股市的日数据，而股市是一周5天制的时间序列数据，因此，一般按照（很多事实证明一般都是错的）下面这样创建文件，File—New--Workfile如图1-1图1-1然后录入数据：打开Quick—Empty Group,从Excel文档直接复制粘贴到下面数据录入窗口，如图1-2图1-2再然后，我们会发现，数据和样本区间不一致，如下图1-3：图1-3相信不少同学在这里就抓狂了，尼玛这EViews咋这么难啊！！！这是因为股市日数据属于不规则类型的时间序列数据即非规范日期数据，关于这类数据如何导入到EViews软件中的问题，相信很多写论文的同学们遇到过，下面将为同学们介绍正确的导入不规则时间序列数据的方法。

首先，创建一个新的Excel文档，把想录入的数据依列排好，注意A列就是数据的日期，后面才是选用的样本数据，而第一行是各数据的英文缩写。

如下图1-4所示：图1-4然后保存文档，例如：另存为：桌面/（注意关闭该Excel文档，文档处于打开状态将影响下面的导入数据步骤）其次，打开EViews点击左上角的File—Open—Foreign Data asWorkfile，如下图1-5所示：图1-5选中桌面/，点击打开，就出现下图1-6的情况：图1-6接下来，直接点击完成，就出现下图1-7：图1-7然后，双击Range最后一步，在弹出的对话框中选择Dated-specificed by date series,这是eviews为我们提供的处理非规范日期数据的工具。

在Date Series 中输入你导入的数据中属于日期的列名。

Eviews格兰杰因果关系检验结果说明Eviews格兰杰因果关系检验结果说明一、经济变量之间的因果性问题计量经济模型的建立过程，本质上是用回归分析工具处理一个经济变量对其他经济变量的依存性问题，但这并不是暗示这个经济变量与其他经济变量间必然存在着因果关系。

由于没有因果关系的变量之间常常有很好的回归拟合，把回归模型的解释变量与被解释变量倒过来也能够拟合得很好，因此回归分析本身不能检验因果关系的存在性，也无法识别因果关系的方向。

假设两个变量，比如国内生产总值GDP和广义货币供给量M，各自都有滞后的分量GDP(-1)，GDP(-2)…，M(-1)，M(-2)，…，显然这两个变量都存在着相互影响的关系。

但现在的问题是:究竟是M引起GDP的变化，还是GDP引起M的变化，或者两者间相互影响都存在反馈，即M引起GDP的变化，同时GDP也引起M的变化。

这些问题的实质是在两个变量间存在时间上的先后关系时，是否能够从统计意义上检验出因果性的方向，即在统计上确定GDP是M的因，还是M是GDP的因，或者M和GDP互为因果。

因果关系研究的有趣例子是回答“先有鸡还是先有蛋”的问题。

1988年有两位学者Walter N. Thurman和Mark E. Fisher用美国1930——1983年鸡蛋产量(EGGS)和鸡的产量(CHICKENS)的年度数据，对此问题进行了统计研究。

他们运用格兰杰的方法检验鸡和蛋之间的因果关系，结果发现，鸡生蛋的假设被拒绝，而蛋生鸡的假设成立，因此，蛋为因，鸡为果，也就是先有蛋。

他们并建议作其他诸如“谁笑在最后谁笑得最好”、“骄傲是失败之母”之类的格兰杰因果检验。

二、格兰杰因果关系检验经济学家开拓了一种可以用来分析变量之间的因果的办法，即格兰杰因果关系检验。

该检验方法为2003年诺贝尔经济学奖得主克莱夫?格兰杰(Clive W. J. Granger)所开创，用于分析经济变量之间的因果关系。

他给因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。

Eviews‎格兰杰因果关‎系检验结果说‎明一、经济变量之间‎的因果性问题‎计量经济模型‎的建立过程，本质上是用回‎归分析工具处‎理一个经济变‎量对其他经济‎变量的依存性‎问题，但这并不是暗‎示这个经济变‎量与其他经济‎变量间必然存‎在着因果关系‎。

由于没有因果‎关系的变量之‎间常常有很好‎的回归拟合，把回归模型的‎解释变量与被‎解释变量倒过‎来也能够拟合‎得很好，因此回归分析‎本身不能检验‎因果关系的存‎在性，也无法识别因‎果关系的方向‎。

假设两个变量‎，比如国内生产‎总值GDP和‎广义货币供给‎量M，各自都有滞后‎的分量GDP‎（-1），GDP（-2）…，M（-1），M（-2），…，显然这两个变‎量都存在着相‎互影响的关系‎。

但现在的问题‎是：究竟是M引起‎G DP的变化‎，还是GDP引‎起M的变化，或者两者间相‎互影响都存在‎反馈，即M引起GD‎P的变化，同时GDP也‎引起M的变化‎。

这些问题的实‎质是在两个变‎量间存在时间‎上的先后关系‎时，是否能够从统‎计意义上检验‎出因果性的方‎向，即在统计上确‎定GDP是M‎的因，还是M是GD‎P的因，或者M和GD‎P互为因果。

因果关系研究‎的有趣例子是‎回答“先有鸡还是先‎有蛋”的问题。

1988年有‎两位学者Wa‎l ter N. Thurma‎n和Mark‎E. Fisher‎用美国193‎0——1983年鸡‎蛋产量（EGGS）和鸡的产量（CHICKE‎N S）的年度数据，对此问题进行‎了统计研究。

他们运用格兰‎杰的方法检验‎鸡和蛋之间的‎因果关系，结果发现，鸡生蛋的假设‎被拒绝，而蛋生鸡的假‎设成立，因此，蛋为因，鸡为果，也就是先有蛋‎。

他们并建议作‎其他诸如“谁笑在最后谁‎笑得最好”、“骄傲是失败之‎母”之类的格兰杰‎因果检验。

二、格兰杰因果关‎系检验经济学家开拓‎了一种可以用‎来分析变量之‎间的因果的办‎法，即格兰杰因果‎关系检验。

该检验方法为‎2003年诺‎贝尔经济学奖‎得主克莱夫·格兰杰（Clive W. J. Grange‎r）所开创，用于分析经济‎变量之间的因‎果关系。

Eviews格兰杰因果关系检验结果说明一、经济变量之间的因果性问题计量经济模型的建立过程，本质上是用回归分析工具处理一个经济变量对其他经济变量的依存性问题，但这并不是暗示这个经济变量与其他经济变量间必然存在着因果关系。

由于没有因果关系的变量之间常常有很好的回归拟合，把回归模型的解释变量与被解释变量倒过来也能够拟合得很好，因此回归分析本身不能检验因果关系的存在性，也无法识别因果关系的方向。

假设两个变量，比如国内生产总值GDP和广义货币供给量M，各自都有滞后的分量GDP （-1），GDP（-2）…，M（-1），M（-2），…，显然这两个变量都存在着相互影响的关系。

但现在的问题是：究竟是M引起GDP的变化，还是GDP引起M的变化，或者两者间相互影响都存在反馈，即M引起GDP的变化，同时GDP也引起M的变化。

这些问题的实质是在两个变量间存在时间上的先后关系时，是否能够从统计意义上检验出因果性的方向，即在统计上确定GDP是M的因，还是M是GDP的因，或者M和GDP互为因果。

因果关系研究的有趣例子是回答“先有鸡还是先有蛋”的问题。

1988年有两位学者Walter N. Thurman和Mark E. Fisher用美国1930——1983年鸡蛋产量（EGGS）和鸡的产量（CHICKENS）的年度数据，对此问题进行了统计研究。

他们运用格兰杰的方法检验鸡和蛋之间的因果关系，结果发现，鸡生蛋的假设被拒绝，而蛋生鸡的假设成立，因此，蛋为因，鸡为果，也就是先有蛋。

他们并建议作其他诸如“谁笑在最后谁笑得最好”、“骄傲是失败之母”之类的格兰杰因果检验。

二、格兰杰因果关系检验经济学家开拓了一种可以用来分析变量之间的因果的办法，即格兰杰因果关系检验。

该检验方法为2003年诺贝尔经济学奖得主克莱夫·格兰杰（Clive W. J. Granger）所开创，用于分析经济变量之间的因果关系。

他给因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。