eviews讲解单位根检验

Eviews残差单位根检验步骤1. 概述Eviews是一种广泛用于计量经济学研究的数据分析软件，它提供了一系列的统计分析工具，其中包括残差单位根检验。

残差单位根检验是判断时间序列数据是否平稳的重要方法之一，本文将介绍在Eviews 软件中进行残差单位根检验的具体步骤。

2. 数据准备在进行残差单位根检验之前，首先需要利用Eviews进行时间序列模型的拟合，得到模型的残差序列。

在Eviews中，可以使用最小二乘法、一般最小二乘法等方法估计时间序列模型，得到残差序列。

以ARMA(p,q)模型为例，其残差序列可以通过以下步骤获取：(1) 打开Eviews软件，导入所需数据；(2) 选择“Quick/Estimate Equation”或“Proc/Estimate Equation”，在弹出的窗口中输入ARMA(p,q)模型的方程形式，点击“OK”进行模型估计；(3) 在估计结果页面，找到残差序列并将其保存。

3. 单位根检验Eviews提供了多种单位根检验的方法，如ADF检验、Phillips-Perron检验等。

下面将以ADF检验为例，介绍在Eviews中进行残差单位根检验的步骤。

(1) 打开Eviews软件，打开保存的残差序列数据；(2) 选择“View/Residual Diagnostics/Unit Root Test”；(3) 在弹出的窗口中选择ADF单位根检验，设置滞后阶数和趋势项，并点击“OK”进行检验；(4) 在ADF单位根检验结果页面，查看检验统计量的数值及其显著性水平，进行单位根检验的判断。

4. 检验结果解读进行残差单位根检验后，需要对检验结果进行解读。

在Eviews中，一般使用的显著性水平为0.05，若检验统计量的值小于相应的临界值，就可以拒绝原假设，即残差序列是平稳的。

相反，若检验统计量的值大于临界值，则不能拒绝原假设，残差序列是非平稳的。

在解读检验结果时，需要注意控制滞后阶数和趋势项的选择，以及检验结果的稳健性和有效性。

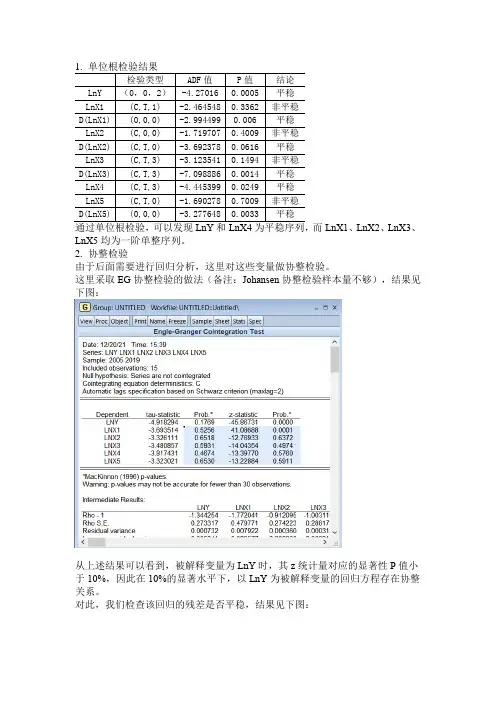
1.单位根检验结果检验类型ADF值P值结论LnY （0，0，2）-4.27016 0.0005 平稳LnX1 (C,T,1) -2.464548 0.3362 非平稳D(LnX1) (0,0,0) -2.994499 0.006 平稳LnX2 (C,0,0) -1.719707 0.4009 非平稳D(LnX2) (C,T,0) -3.692378 0.0616 平稳LnX3 (C,T,3) -3.123541 0.1494 非平稳D(LnX3) (C,T,3) -7.098886 0.0014 平稳LnX4 (C,T,3) -4.445399 0.0249 平稳LnX5 (C,T,0) -1.690278 0.7009 非平稳D(LnX5) (0,0,0) -3.277648 0.0033 平稳通过单位根检验，可以发现LnY和LnX4为平稳序列，而LnX1、LnX2、LnX3、LnX5均为一阶单整序列。

2.协整检验由于后面需要进行回归分析，这里对这些变量做协整检验。

这里采取EG协整检验的做法（备注：Johansen协整检验样本量不够），结果见下图：从上述结果可以看到，被解释变量为LnY时，其z统计量对应的显著性P值小于10%，因此在10%的显著水平下，以LnY为被解释变量的回归方程存在协整关系。

对此，我们检查该回归的残差是否平稳，结果见下图：由残差的单位根检验结果可以看出，此时残差为平稳序列，即该回归存在协整关系。

3.格兰杰因果关系检验由前面的协整检验知LnY与解释变量存在长期的均衡关系，在此基础上，我们对其进行格兰杰因果关系检验。

从上图可以看出LnX1和LnX5不是LnY的格兰杰原因，而LnX2、LnX3、LnX4均是LnY的格兰杰原因，因此我们将建立以LnY为被解释变量，以LnX2、LnX3、LnX4为解释变量的回归。

4.回归结果首先对LnY与LnX2、LnX3、LnX4做协整检验，结果如下：从结果可以看出被解释变量为LnY时，其tau统计量对应的显著性P值小于10%，因此在10%的显著水平下，以LnY为被解释变量的回归存在协整关系。

eviews各种检验（⼀）、ADF是单位根检验，第⼀列数据y做ADF检验，结果如下Null Hypothesis: Y has a unit rootExogenous: Constant, Linear Trend 外因的Lag Length: 0 (Automatic based on SIC, MAXLAG=10)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -3.820038 0.0213Test critical values: 1% level -4.0987415% level -3.47727510% level -3.166190在1%⽔平上拒绝原假设，序列y存在单位根，为不平稳序列。

但在5%、10%⽔平上均接受原假设，认为y平稳。

对y进⾏⼀阶差分，差分后进⾏ADF检验：Null Hypothesis: Y has a unit rootExogenous: NoneLag Length: 0 (Automatic based on SIC, MAXLAG=10)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -9.328245 0.0000Test critical values: 1% level -2.5999345% level -1.94574510% level -1.613633可见，在各⽔平上y都是平稳的。

因此，可以把原序列y看做⼀阶单整。

第⼆列xADF检验如下：Null Hypothesis: X has a unit rootExogenous: Constant, Linear TrendLag Length: 0 (Automatic based on SIC, MAXLAG=10)t-Statistic Prob.* Augmented Dickey-Fuller test statistic -3.216737 0.0898Test critical values: 1% level -4.0987415% level -3.47727510% level -3.166190在1%、5%⽔平上拒绝原假设，序列x存在单位根，为不平稳序列。

ADF检验就是单位根检验，把数据输入Eviews之后，点击左上角的View--Unit Root Test,（但好
像更好用一些），之后可以选择一阶、二阶差分之后的序列是否存在单位根，同时可以选检验的方程中是否存在存在趋势项、常数项等。

一般进行ADF检验要分3步：
1 对原始时间序列进行检验，此时第二项选level，第三项选None.如果没通过检验，说明原始时间序列不平稳；
2 对原始时间序列进行一阶差分后再检验，即第二项选1st difference，第三项选intercept,若仍然未通过检验，则需要进行二次差分变换；
3 二次差分序列的检验，即第二项选择2nd difference ，第四项选择Trend and intercept.一般到此时间序列就平稳了！
看结果：
1%，5%，10%指的是显著水平，如果ADF检验值（t值）大于某显著水平值（一般是5%），则不通过检验，即存在单位根（不平稳），此时，可通过一阶差分再来查看单位根是否平稳，p值指的是接受原假设的概率。

在报告上的写法：
：r=0
H
: r=1
H
1
，序列有单位根，非平缓。

反之……
如果ADF检验值>临界值，则接受H
（注：H
的写法，选中要设置为下标的字母，点击菜单栏格式——字体，选择效
果中的下标，确定。

或直接选中的那个红色项进行格式设置）
操作：图/line&symbol。

单位根检验的eviews操作单位根检验是时间序列分析中常用的方法，用于检测序列是否具有随机游走性。

本文将介绍如何在Eviews中进行单位根检验。

首先，打开Eviews软件，导入要进行单位根检验的时间序列数据。

接下来，依次选择“View”-“Coefficient Tests”-“Unit Root Test”。

在“Unit Root Test”窗口中，首先需要在右侧“Specification”栏选择要进行的单位根检验方法。

通常使用的有ADF（Augmented Dickey-Fuller）检验、PP（Phillips-Perron）检验、KPSS（Kwiatkowski-Phillips-Schmidt-Shin）检验等方法。

这里以ADF检验为例。

在“ADF Specification”选项卡中，可以输入滞后阶数和趋势项。

滞后阶数一般为0或1，趋势项可以是无、常数项或常数项和趋势项。

一般情况下，选择一次滞后和常数项即可。

接下来，点击“OK”按钮即可进行单位根检验。

分析结果将会显示在新打开的“Unit Root Test Results”窗口中。

其中，关注ADF统计量及其p值。

当ADF统计量的绝对值小于临界值，或者p值大于0.05时，说明序列存在单位根，即不平稳；否则可以拒绝存在单位根的假设，说明序列是平稳的。

另外，在“Unit Root Test Results”窗口中还可以看到检验时的样本量、滞后阶数、趋势项、估计方程等信息，方便用户进行进一步分析。

除了ADF检验以外，PP检验和KPSS检验的操作也与ADF检验类似，不再赘述。

总之，单位根检验是时间序列分析中常用的方法，在Eviews中进行单位根检验非常方便，只需要几步操作即可得到结果，为后续的进一步分析提供基础。

我国1978-2003年GDP数据平稳性分析实验报告
开机进入eviews系统，建立时间序列，导入以下数据：
x(年度）y（GDP）x(年度）y（GDP）
1978 1991
1979 1992
1980 1993
1981 1994
1982 1995
1983 1996
1984 7171 1997
1985 1998
1986 1999
1987 2000
1988 2001
1989 2002
1990 2003
绘制y的时序图可初步判断该序列是不平稳的。

如图所示：
120000
100000
80000
60000
40000
20000
78808284868890929496980002
Y
接着进行单位根检验：
输入y，弹出如下窗口：
选择ADF检验，level（水平序列），trend and intercept，滞后期数设为2.得到：
可知，在原假设下，单位根的t检验统计量的值为，比在1％，5％，10％这三个显著性水平下的单位根检验的临界值都要大，故接受原假设，可知该时间序列存在单位根，为非平稳序列。

继续对该序列的一阶差分进行检验。

得到
单位根的t检验统计量的值为，比在10％显著性水平下的单位根检验的临界值要小，即拒绝原假设，表明该序列的一阶差分为平稳序列。