齿轮系统的接触模态分析

齿轮传动系统的动力学与模态分析刘荫荫;熊曼辰【摘要】为了提高齿轮设计的准确性，结合UG软件参数化建模功能，建立齿轮传动三维实体模型。

利用ADAMS软件对齿轮传动系统进行了动力学分析，在高速传动中施加实际传动载荷，得到了齿轮传动系统的振动频率范围和高频率点。

通过 ANSYS Workbench软件对齿轮传动系统和单一齿轮模型进行模态分析，得到齿轮传动系统和齿轮模型的固有频率和振型，通过与动力学分析得到的频率进行对比，验证了齿轮传动系统的设计准确性，从而为今后齿轮的传动分析提供了数据支持，并为传动过程中的故障分析提供了参考。

%To improve the accuracy of the gear design,build three-dimensional solid model of the transmission gear in the parametric modeling module of UG software.Dynamic analysis of gear transmission system by using ADAMS software and actual load applied in high-speed gear transmission were finished,based on the above conditions,the vibration frequency range and high frequency point can be obtained.ANSYS Workbench was used to analyze the modal of gear transmission sys-tem and a single gear and get both the natural frequencies and mode shapes,through comparing the frequency gained by dy-namics analysis,verified the design accuracy of gear transmission system and provided data support for the gear transmission after analysis and a reference for failure analysis in the transmission process.【期刊名称】《新技术新工艺》【年(卷),期】2014(000)009【总页数】4页(P100-103)【关键词】ADAMS;动力学分析;ANSYS Workbench;模态分析;固有频率【作者】刘荫荫;熊曼辰【作者单位】昆明理工大学机电工程学院，云南昆明 650000;昆明理工大学机电工程学院，云南昆明 650000【正文语种】中文【中图分类】TH132.4渐开线齿轮是一种重要的机械零件，因为齿轮传动的平稳性而在高速传动设置中作为传动装置的核心部分起重要作用。

齿轮的精确建模及其接触应力有限元分析齿轮是机械设备中重要的元件，它们的使用范围十分广泛，在它们的设计和制造中，准确的建模和模拟计算对于确定传动性能和寿命至关重要。

然而，齿轮传动存在不确定性和实际复杂度，传统的理论分析方法难以完全表述齿轮传动的特性，因此不能准确预测传动系统的状态及性能。

随着计算机技术的不断发展，由于有限元分析技术的出现，对齿轮传动性能和寿命的计算变得十分方便。

以精确建模及其接触应力有限元分析为目标，可以精确模拟齿轮传动的接触状态和接触应力，从而更好地表达系统性能、可靠性和可持续性，实现传动性能和精度的优化。

首先，要正确建模齿轮的接触过程，必须完善模型的拓扑结构和几何结构。

若要真实地反映齿轮接触过程，需要建立具有齿轮几何和物理特性的有限元模型，并分析参数要求，建立模型以进行计算。

其次，要准确模拟出齿轮接触过程，必须准确地定义接触点的表面特性；为了获得准确的接触应力分布，必须建立解析模型，采用物理尺度分析参数，综合考虑不同材料的特性，并考虑载荷的特点，以保证模型的准确性和可靠性。

此外，需要考虑齿轮接触过程中的多相现象。

实际情况下，在齿轮接触过程中，热变形和武豆形齿面接触过程会产生润滑膜，需要考虑润滑膜的影响，以获得更准确的模拟结果。

在实际计算中，润滑膜会影响接触应力的分布，因此，精确分析齿轮接触过程中的润滑膜结构及其特性是非常必要的。

此外，有限元法用于齿轮传动性能分析时，也必须考虑轴、轴承、定位器及其他各种传动元件的性能。

轴承等各种元件的设计，会影响齿轮的接触侧的咬合情况，因此也会影响齿轮的接触状态和接触应力。

在完成模型的建立后，就可以使用有限元分析技术，通过不断改变不同的参数和条件，对齿轮传动性能进行精确模拟，并得出合理的结果和结论。

使用该方法，可以分析齿轮传动系统中各种参数和齿轮及其接触表面的特性，比如形象、弯曲度、几何曲线、接触条件等，可以得出齿轮传动的最佳设计参数，提高传动精度和可靠性。

根据图1可知赫兹接触理论模型的接触半宽为：式中，E1、E2为齿轮1、齿轮2、齿轮2的泊松比；L为接触面长度；最大值；F n为外力；R1为齿轮1的分度圆半径；的分度圆半径；b为接触面半宽。

赫兹接触理论模型的接触应力为：（考虑齿轮传动中小齿轮单对齿啮合系数Z B ；节点区域系数Z H ；弹性系数Z E ；重合度系数Z L ；螺旋角系数Z β；荷系数K ；太阳轮上转矩T 1；齿轮传动比i ，得到最大接触应力为：（由弹性理论可得内力与体积力的关系方程为：体内的应力与表面力存在的边界条件为：式中，F Sx 、F Sy 、F Sz 为表面力在x 为表面外法线方向余弦。

对于具有接触面的结构，在承受荷载的过程中，面的状态变化影响接触体的应力场，接触状态。

分析接触问题的常用方法有数学规划法、元法和有限元法，对复杂的接触问题常用有限元法。

有限接触点的柔度方程组为：式中，δi ，A 和C Aij 为物体A 在接触点子矩阵；δi ，B 和C Bij 为物体B 在接触点矩阵；m 1为外力作用点数；R Ak 为载荷向量。

由于两相互接触物体一般不会产生渗透，两接触面间的接触关系以阻止穿透的发生，表面接触，存在大变形的摩擦接触时可引入额外因子虽然拉朗格朗日乘子模型能够得到接近零的穿透量，但计算量较大。

当允许有较小的穿透量时可使得接触状态图1赫兹接触理论模型F nR 1σHmax2bR 2F n图2基于UG的齿轮对接触仿真模型图3基于UG的齿轮对接触分析位移云图得到齿轮对的应力云图如图4所示。

可知齿轮对在接触区的应力较大，且最大应力发生在齿轮对接触面上，与实际情况相符，齿轮对的最大应力为15.53MPa，远小于材料的屈服应力。

通过对齿轮对接触面处的接触分析可进一步了解齿轮对的传动性能情况。

图4基于UG的齿轮对接触分析应力云图得到齿轮对的接触力与接触压力云图如图5所示。

将视图进行局部选择，图5（a）为齿轮对接触面处接触力云图，图5（b）为齿轮对接触面处的接触压力云图。

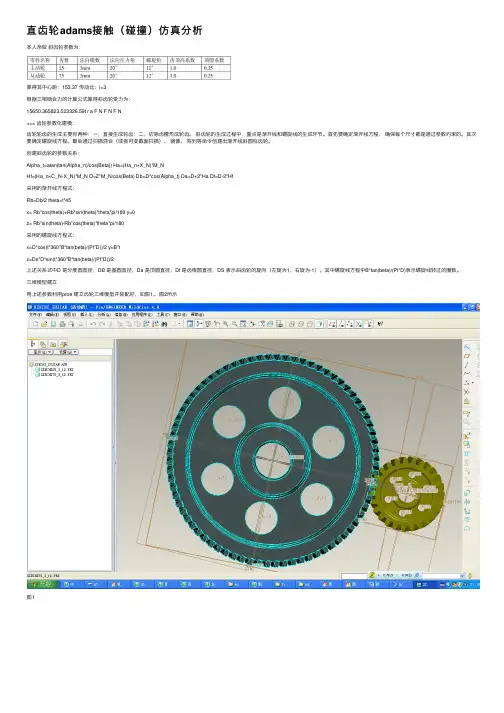
直齿轮adams接触（碰撞）仿真分析本⼈亲做斜齿轮参数为：算得其中⼼距：153.37 传动⽐：i=3根据三相啮合⼒的计算公式算得斜齿轮受⼒为：15650.365823.523326.59t r a F N F N F N=== 齿轮参数化建模：齿轮轮齿的⽣成主要有两种：⼀，直接⽣成轮齿；⼆，切除齿槽形成轮齿。

斜齿轮的⽣成过程中，重点是渐开线和螺旋线的⽣成环节。

⾸先要确定渐开线⽅程，确保每个尺⼨都是通过参数约束的。

其次要确定螺旋线⽅程。

最后通过扫描混合（或者可变截⾯扫描）、镜像、阵列等命令创建出渐开线斜圆柱齿轮。

创建斜齿轮的参数关系：Alpha_t=atan(tan(Alpha_n)/cos(Beta)) Ha=(Ha_n+X_N)*M_NHf=(Ha_n+C_N-X_N)*M_N D=Z*M_N/cos(Beta) Db=D*cos(Alpha_t) Da=D+2*Ha Df=D-2*Hf采⽤的渐开线⽅程式：Rb=Db/2 theta=t*45x= Rb*cos(theta)+Rb*sin(theta)*theta*pi/180 y=0z= Rb*sin(theta)-Rb*cos(theta)*theta*pi/180采⽤的螺旋线⽅程式：x=D*cos(t*360*B*tan(beta)/(PI*D))/2 y=B*tz=Ds*D*sin(t*360*B*tan(beta)/(PI*D))/2上述关系式中D 是分度圆直径，DB 是基圆直径，Da 是顶圆直径，Df 是齿根圆直径，DS 表⽰斜齿轮的旋向（左旋为1，右旋为-1）。

其中螺旋线⽅程中B*tan(beta)/(PI*D)表⽰螺旋线转过的圈数。

三维模型建⽴⽤上述参数利⽤proe 建⽴齿轮三维模型并装配好，如图1,、图2所⽰图1图2将三维模型导⼊adams定义导⼊模型后，逐步进⾏：材料属性定义，添加约束，添加驱动，添加负载，添加接触⼒，然后得到仿真处理前期⼯作，如图3，图4所⽰图3图4、仿真后处理仿真后处理得到斜齿轮三个⽅向上波动图和均值。

基于UG的某行星齿轮流量计齿轮系统的模态分析UG软件作为广泛应用于机械设计和制造领域的软件平台，为工程师提供了全面的设计、分析和仿真功能。

本文将基于UG软件对某行星齿轮流量计齿轮系统进行模态分析，并深入探讨齿轮系统的性能。

行星齿轮流量计是一种常用于测量液体或气体体积流量的装置，而齿轮系统是其核心部件之一。

本设计采用了行星齿轮系统，由一组内啮合于齿轮挂架周边的小齿轮与一组密合外啮合的大齿轮构成，并通过转动传递动力。

齿轮系统的稳定性和运行效率对流量计的性能有着至关重要的影响。

在基于UG软件进行模态分析前，首先需要建立模型。

采用Solid Edge软件建立了整个行星齿轮流量计的三维模型，并将该模型导入到UG平台进行分析。

在建立模型时，需要注意每个齿轮之间的啮合配合尺寸与公差要求，以保证齿轮系统的运转稳定。

模态分析主要是对齿轮系统的振动响应情况进行分析。

在UG的求解过程中，将根据齿轮系统的自由度及其几何结构、材料属性、质量等因素，计算系统在某一特定条件下的固有频率和固有振型。

通常情况下，系统的前几个固有频率相对最低的自然频率决定了某些环节的构建机件的准则。

根据计算结果，可以对设计进行优化和改进，从而提高齿轮系统的稳定性和运行效率。

该行星齿轮流量计齿轮系统经模态分析计算，得到了其前三阶模态振型和频率。

在分析过程中，发现齿轮系统存在较为明显的固有频率，并且共振振动趋势明显，震荡范围也比较广泛。

在实际应用中，如果行星齿轮流量计的齿轮系统运转时发现存在这样的问题，就需要对设计加以优化，以避免共振引起的机械故障。

在行星齿轮流量计齿轮系统中，行星齿轮是一个重要的组件，其优化设计将对系统的动力学性能产生显著影响。

通过调整行星齿轮半径、齿轮数和轴向距等参数，可以改变系统的自振频率和响应性能，从而优化齿轮系统的作用性能。

总之，基于UG软件进行的行星齿轮流量计齿轮系统模态分析极大地提升了该系统的稳定性和运行效率，为其在实际工程应用中提供了强有力的保障。

基于ANSYS的齿轮弯曲应力、接触应力以及模态分析随着汽车性能和速度的提高，对变速箱齿轮也提出了更高的要求。

为较好地改善齿轮传动性能，有必要对齿轮进行静力学以及动力学分析。

对于齿轮的静力学分析，本文利用ANSYS对齿轮进行了齿根弯曲应力分析以及齿轮接触应力分析。

对于齿轮的动力学分析，本文利用ANSYS对其进行了模态分析，提取了齿轮的前十阶固有频率和固有振型。

最后实验表明，基于ANSYS的齿轮弯曲应力和接触应力相比较传统方法具有一定的裕度，而模态分析能较形象地展现其振型。

标签：齿轮；弯曲应力；接触应力；模态分析引言随着汽车性能和速度的提高，对变速箱齿轮也提出了更高的要求。

改善齿轮传动性能成为齿轮设计中的重要内容。

为了避免由于齿轮接触疲劳而引发的行驶事故，有必要对齿轮的齿根弯曲应力和齿面接触应力进行分析和评估。

同理，为避免由于齿轮共振引起的轮体破坏，有必要对齿轮进行固有特性分析，通过调整齿轮的固有振动频率使其共振转速离开工作转速。

齿轮的工作寿命与最大弯曲应力值的六次方成反比，因此最大弯曲应力略微减小，齿轮工作寿命即会大大提高[1]。

齿轮的最大弯曲应力往往出现在齿轮的齿根过渡曲线处，因此精确计算渐开线齿轮齿根过渡曲线处的应力，进而合理设计过渡曲线，对延长齿轮工作寿命、提高齿轮承载能力至关重要。

为了进行齿面接触强度计算，分析齿面失效和润滑状态，必须分析齿面的接触应力。

经典的齿面接触应力计算公式是建立在弹性力学基础上，而对于齿轮的接触强度计算均以两平行圆柱体对压的赫兹公式为基础。

但由于齿轮副啮合齿面的几何形状十分复杂，采用上面的方法准确计算轮齿应力和载荷分配等问题非常困难甚至无法实现。

随着计算机的普及，齿轮接触问题的数值解法获得了越来越广泛的应用。

齿轮副在工作时，在内部和外部激励下将发生机械振动。

振动系统的固有特性，一般包括固有频率和主振型，它是系统的动态特性之一，同时也可以作为其它动力学分析的起点，对系统的动态响应、动载荷的产生与传递以及系统振动的形式等都具有重要的影响。

齿轮副的接触分析及模态分析程* 2018101171.齿轮的相关参数齿顶直径：24齿底直径：20齿数：10厚度：4密度：7.8E3弹性模量：2.06E11摩擦系数：0.1中心距：442.建立模型从主菜单中选择Preference命令，在对话框中选择“Structural”复选框定义单元类型主菜单中选择Preprocessor>Element Type>Add/Edit/Delete，设置“Solid”，“4node 182”在Element Types对话框中单击【Options】弹出单元选项对话框，对PLANE182单元进行设置定义实常数选择Preprocessor>Real Constants>Add/Edit/Delete，设置常数单元类型，中将厚度设置为4定义材料属性从主菜单中选择Preprocessor>Material Props>Material Models，设置材料的弹性模量EX=2.06E11、泊松比PRXY=0.3，材料密度为7.8E3，摩擦系数为0.1建立齿轮面模型将当前坐标系设置为总体柱坐标系。

从实用菜单中选择WorkPlane>Change Actives CS to>Global Cylindrical定义关键点：Preprocessor>Modeling>Create>Keypoints>In Active CS，编号1（20，0）；定义辅助点：Preprocessor>Modeling>Create>Keypoints>In Active CS偏移工作平面到给定位置选择WorkPlane>Offset WP to>Keypoints +，选择110号辅助点旋转工作平面选择WorkPlane>Offset WP by Increments，在“XY,YZ,ZX,ZXAngles”文本框中输入-50,0,0将激活的坐标系设置为工作平面坐标系：选择WorkPlane>Change Actives CS to>Working Plane建立第二个关键点，Preprocessor>Modeling>Create>Keypoints>In Active CS ，2（12.838，0）设置总体柱坐标系，选择WorkPlane>Change Actives CSto>Global Cylindrical建立其余辅助点：Preprocessor>Modeling>Create>Keypoints>In Active CS，设置编号依次为120，130，140，150，160，其坐标依次为（16，43）、（16，46）、（16，49）、（16，52）、（16，55）a.偏移工作平面到给定位置选择WorkPlane>Offset WP to>Keypoints +，选择120号辅助点b.旋转工作平面，选择WorkPlane>Offset WP by Increments，在“XY,YZ,ZX,ZXAngles”文本框中输入3,0,0c. 将激活的坐标系设置为工作平面坐标系：选择WorkPlane>Change Actives CS to>Working Plane建立第三个关键点：Preprocessor>Modeling>Create>Keypoints>In Active CS，3（13.676，0）重复以上a—c，建立其余的辅助点和关键点，分别把工作平面平移到编号为130，140，150，160的辅助点，然后旋转工作平面，旋转角度均为3,0,0，再讲工作平面设为当前坐标系，在工作平面中分别建立编号为4，5，6，7的关键点，其坐标依次为（14.513，0）、（15.351，0）、（16.189，0）、（17.027，0）建立编号为8，9，10的关键点，选择WorkPlane>Change Actives CSto>Global Cylindrical、Preprocessor>Modeling>Create>Keypoints>In Active CS，建立关键点8（24，9.875）、9（24，13）、10（20，5）创建圆弧线选择Preprocessor>Modeling>Create>Lines>Straight Line，按顺序连接关键点，再将其相加使其成为一条线Preprocessor>Modeling>Operate>Booleans>Add>Lines，删除原来的线偏移工作平面到总坐标系的原点：WorkPlane>Offset WP to>Global Origin将工作平面与总体坐标系对齐：WorkPlane>Align WP with>Global Cartesian将工作平面旋转13°，选择WorkPlane>Offset WP by Increments，在“XY,YZ,ZX Angles”文本框中输入13,0,0将所有线沿着X-Z面进行镜像（在Y方向），选择Preprocessor>Modeling>Reflect>Lines把每个齿顶上的两条线粘起来，选择Preprocessor>Modeling>Operate>Booleans>Glue>Lines 把齿顶上的两条线加起来，成为一条线，Preprocessor>Modeling>Operate>Booleans>Add>Lines 在柱坐标系下复制线，设置坐标系选择WorkPlane>Change Actives CS to>Global Cylindrical，主菜单选择Preprocessor>Modeling>Copy>Lines把齿底上的所有线粘起来，Preprocessor>Modeling>Operate>Booleans>Glue>Lines，分别选择齿低的两条线，再把齿底上的所有线加起来把所有线粘起来，选择Preprocessor>Modeling>Operate>Booleans>Glue>Lines用当前定义的所有线生成一个面，选择Preprocessor>Modeling>Create>Areas>Arbitrary>By Lines创建圆面，选择Preprocessor>Modeling>Create>Areas>Circle>Solid Circle从齿轮面中减去圆面，选择Preprocessor>Modeling>Operate>Booleans>Subtract>Areas在直角坐标系下复制面，设置坐标系选择WorkPlane>Change Actives CS to>Global Cartesian，复制Preprocessor>Modeling>Copy>Areas创建局部坐标系，选择WorkPlane>Local Coordinate Systems>Create Local CS>At Specified Loc+将当前坐标系设置为局部坐标系，选择WorkPlane>Change Actives CS to>Specified Coord Sys在局部坐标系下复制面，选择Preprocessor>Modeling>Copy>Areas删除第二个面，选择Preprocessor>Modeling>Delete>Area and Below，生成结果划分网格对齿面划分网格，选择Preprocessor>Meshing>MeshTool定义接触对（1）从应用菜单中选择Select>Entities，在类型下拉列表中选“Lines”,点击【Apply】（2）打开先选择对话框，选择一个齿轮上可能与另一个齿轮相接触的线，点击【OK】（3）在实体选择对话框中选择“Nodes”,在选择方式中选择“Attached to ”,在单选列表中选择“Lines, all”（4）选择Select>Como/Assembly>Create Component，在“Component name”文本框中输入”node1”,点击【OK】（5）从实用菜单中选择Select>Everything（6）在实体选择对话框中在类型下拉列表中选“Lines”,选择方式选“By Num/Pick”,点击【Apply】，弹出线选择对话框，选择另一个齿轮上可能与前一个齿轮相接触的线，点击【OK】在实体选择对话框中选择“Nodes”,在选择方式中选择“Attached to ”,在单选列表中选择“Lines, all”（7）选择Select>Como/Assembly>Create Component，在“Component name”文本框中输入”node2”,点击【OK】（8）从实用菜单中选择Select>Everything（9）点击工具栏中的【接触定义向导】（10）选择工具条中的第一项，会打开下一步操作向导，在对话框中选择”NODE2”，并点击【Next】（12）在对话框选取“NODE1”，点击【NEXT】（13）点击【Create】,建立接触对3.定义边界条件并求解（1）施加位移边界，选择WorkPlane>Change Actives CS to>Global Cylindrical；选择Preprocessor>Modeling>Move/Modify>Rotate Node CS>To Active CS，打开节点选择的对话框，要求选择欲旋转的坐标系的节点；选择第一个齿轮内径上所有节点，从实用菜单中选择Select>Entities，弹出实体选择对话框，选择第一个齿轮内径上所有的节点选择Solution>Define Loads>Apply>Structural>Displacement>on Nodes，点开节点选择对话框，要求选择欲施加位移约束的节点。

齿轮传动轴的动态特性测试与模态分析引言齿轮传动系统在机械装置中扮演着关键的角色，它通过齿轮的相互啮合传递力与运动。

在实际应用中，齿轮传动轴的动态特性对于确保传动系统的稳定性、可靠性以及寿命都起着至关重要的作用。

本文将深入探讨齿轮传动轴的动态特性测试与模态分析，以提供对传动系统性能优化的基础理论和实践指导。

一、齿轮传动轴动态特性的测试方法1. 强制激励法强制激励法是一种常用的齿轮传动轴动态测试方法，它通过对传动轴施加特定的荷载或力矩，从而观察其自由振动状态下的响应特性。

一般情况下，引入外加力或力矩后，通过合适的传感器采集传动轴的振动响应信号，并将其转化为频谱图分析，可以获得传动轴在不同激励条件下的振动模态。

2. 自由振动法自由振动法是另一种常用的齿轮传动轴动态测试方法，它在没有外界强制激励的情况下，通过对传动轴施加初速度或初位移，观察其自由振动过程中的响应特性。

测试时应尽量降低传动轴的阻尼，以减小振动信号的衰减，并采集振动响应信号进行频谱分析，进而得到传动轴的振动模态。

二、齿轮传动轴的模态分析1. 模态分析的基本原理模态分析是一种通过对某个结构或系统施加激励并测量其振动响应，来研究其特定振动模态的方法。

在齿轮传动轴的模态分析中，通过将传动轴固定在一端，施加激励并测量振动响应，可以得到传动轴的自由振动模态频率、振型和阻尼比等信息。

这些信息对于齿轮传动轴的动态特性和谐波分析等方面具有重要的意义。

2. 模态分析的步骤a. 激励源与传感器的安装：在模态分析实验中，需要选择合适的激励源，如锤击法、电磁激振器等，并通过传感器采集传动轴的振动信号。

传感器通常安装在传动轴的不同位置，以获取全面的振动模态信息。

b. 数据采集与处理：采集传感器测得的振动信号，并对其进行滤波和放大等处理。

通常使用频谱分析方法将时域信号转换为频域信号，得到传动轴不同频率上的振动响应特性。

c. 振型识别与模态提取：通过对频谱图的分析，可以识别出传动轴的振动模态，并提取出相应的模态参数，如频率、振型和阻尼比。

基于ANSYS的齿轮静力学分析及模态分析齿轮是一种常用的机械传动装置，广泛应用于机械传动系统中。

在设计齿轮时，常常需要进行静力学分析和模态分析，以确保其性能和可靠性。

基于ANSYS软件的齿轮静力学分析和模态分析方法是一种常用的设计方法。

首先，进行齿轮静力学分析需要获取齿轮的几何参数和材料性质。

几何参数包括齿轮的齿数、模数、齿宽等，材料性质包括齿轮的材料弹性模量、泊松比等。

然后，使用ANSYS软件建立齿轮的三维有限元模型，并进行网格划分。

在建立完有限元模型之后，进行齿轮静力学分析。

首先要定义齿轮的边界条件和载荷情况。

边界条件包括固定约束和辅助约束，以模拟实际应用中的固定情况。

载荷情况包括齿轮的输入转矩和速度，以及传递给齿轮的负载。

然后，应用静力学方程，利用ANSYS软件进行静力学计算，得到齿轮的应力和变形分布情况。

通过齿轮静力学分析，可以评估齿轮的传动性能和承载能力。

根据分析结果，可以进行结构优化，以提高齿轮的性能和可靠性。

除了静力学分析，模态分析也是齿轮设计中的重要环节。

模态分析主要用于研究齿轮的固有振动特性。

通过模态分析可以确定齿轮的固有频率和振型，以及可能产生共振的模态。

在模态分析中，需要定义齿轮的材料性质和几何参数，建立三维有限元模型，并进行网格划分。

然后，通过ANSYS软件进行模态分析，得到齿轮的固有频率和振型。

通过模态分析，可以了解齿轮的振动特性和共振情况，以及可能导致振动问题的关键频率。

根据分析结果，可以采取措施来避免共振问题，提高齿轮的振动稳定性。

总的来说，基于ANSYS的齿轮静力学分析和模态分析方法可以帮助工程师了解齿轮的承载性能和振动特性，以指导齿轮的设计和优化。

这些分析结果对于提高齿轮的传动效率和可靠性非常重要。

因此，建议在齿轮设计过程中，尽量采用ANSYS软件进行静力学分析和模态分析，以确保设计的准确性和可靠性。

基于ANSYS的齿轮静力学分析及模态分析齿轮是常用的动力传动装置，广泛应用于机械设备中。

在设计齿轮传动系统时，静力学分析和模态分析是非常重要的步骤。

本文将重点介绍基于ANSYS软件进行齿轮静力学分析和模态分析的方法和步骤。

1.齿轮静力学分析齿轮静力学分析旨在分析齿轮传动系统在静态负载下的应力和变形情况。

以下是基于ANSYS进行齿轮静力学分析的步骤：步骤1：几何建模使用ANSYS中的几何建模工具创建齿轮的三维模型。

确保模型准确地包含所有齿轮的几何特征。

步骤2：材料定义使用ANSYS的材料库定义齿轮材料的力学性质，例如弹性模量、泊松比和密度等。

步骤3：加载条件定义定义加载条件，包括对齿轮的力或力矩、支撑条件等。

加载条件应符合实际使用情况。

步骤4：网格划分使用ANSYS的网格划分工具对齿轮模型进行网格划分。

确保网格划分足够细致以捕捉齿轮的几何特征。

步骤5：模型求解使用ANSYS中的有限元分析功能对齿轮模型进行求解，得到齿轮在加载条件下的应力和变形分布情况。

步骤6：结果分析分析模型求解结果，评估齿轮的强度和刚度。

如果发现应力或变形过大的区域，需要进行相应的结构优化。

2.齿轮模态分析齿轮模态分析用于确定齿轮传动系统的固有频率和模态形态。

以下是基于ANSYS进行齿轮模态分析的步骤：步骤1：几何建模同齿轮静力学分析中的步骤1步骤2：材料定义同齿轮静力学分析中的步骤2步骤3：加载条件定义齿轮模态分析中，加载条件通常为空载条件。

即不施加任何外力或力矩。

步骤4：网格划分同齿轮静力学分析中的步骤4步骤5：模型求解使用ANSYS中的模态分析功能对齿轮模型进行求解，得到其固有频率和模态形态。

步骤6：结果分析分析模型求解结果，确定齿轮传动系统的固有频率和模态形态。

根据结果可以评估齿轮传动系统的动力特性和工作稳定性。

综上所述，基于ANSYS进行齿轮静力学分析和模态分析可以有效地评估齿轮传动系统的强度、刚度和动力特性。

这些分析结果对于优化齿轮设计和确保齿轮传动系统的正常工作非常重要。

齿轮接触问题问题描述1、求解目的一对啮合的齿轮在工作的时候产生接触，分析其接触的位置、面积和接触力的大小。

2、尺寸描述标准齿轮齿顶直径24，齿底直径20，齿数10，厚度4，弹性模量2.06e11，摩擦系数0.1，中心距44一、问题分析1、单元类型分析element style在进行有限元分析的时候，首先应该根据分析问题的几何结构、分析类型和所分析的问题精度要求，选定适合具体分析的单元类型。

在本题目中，选择4节点的四边形单元plane182，它不仅可以计算平面应力问题，还可以用于分析平面应变，轴对称问题。

2、建模分析由于分析问题需要，只需要建立齿轮的一个截面。

首先创建齿轮渐开线轮廓关键点keypoints，然后通过连接关键点的形式创建线line，运用布尔运算的add操作将线加在一起。

由于齿轮具有对称的结构，所以创建完一个渐开线齿廓后，可以通过复制映射的方法，创建其它的齿廓，最后将所有的渐开线齿廓运用布尔运算加（add）在一起，就得到整个齿轮。

最后通过映射操作，得到另一个齿轮。

1实体模型如图示（1）对前处理完成的模型进行划分网格操作，如图示（2）对齿轮施加约束，约束加在两个齿轮的回转中心处的24个节点上，约束类型为ALL DOF如上图示。

3、齿轮接触点处的变形图，接触点处齿轮受到另一个齿轮的挤压力的作用会产生一定的变形，如图示，其中黑线表示变形后的位置。

4接触应力（1）两个齿轮接触点处的应力contack pressure（2）等效应力von mises四，报告总结有限元分析的步骤是：前处理，加载与求解，后处理。

其中前处理的建模是基础，准确无误的建立好模型才能在进行完网格划分后，对所建立的模型进行正确的求解，得到正确的结果。

对所求解的问题要有正确的建模分析，根据它的求解目的有正确的单元类型分析，同时要又正确的有限元分析。

根据后处理得到的结果分析实际问题的可靠性，安全性等等。

齿轮系统动⼒学及接触问题摘要齿轮⾮线性接触特性及啮合刚度的研究对于齿轮接触特性的研究，可以采⽤解析法和数值法。

解析法包括材料⼒学计算法和弹性⼒学计算法等，数值法包括接触问题的有限元法和边界元法。

齿轮接触特性计算的解析法把啮合轮齿简化为两圆柱体通过Hertz公式计算接触应⼒及接触变形。

但由于齿轮齿廓曲率半径沿齿⾯变化，加之Hertz公式不能确定齿⾯接触疲劳强度计算中的累积塑性变形，因此其计算结果较为近似往往⽤修正系数(动载系数、齿向载荷分布系数、齿间载荷分配系数等)对接触应⼒进⾏修正。

对于齿轮接触变形的计算公式，G Lundberg、H .Winter、梅泽清彦、寺内喜男等分别采⽤材料⼒学和弹性⼒学⽅法进⾏了推导。

接触问题数值⽅法的研究始于70年代中期，⽽后得到⼴泛应⽤。

0.C. Zienkiewicz、A.Fr ancevilla、N .Okamoto、 J. T. Stadter、T .D .Sachdeva等分别⽤刚度矩阵修正法或间隙单元法研究了⼆维及三维弹性接触问题。

J.Tseng、陈万吉、李润⽅等提出了接触问题有限元混合法。

该⽅法以接触内⼒作为基本未知量，将整个系统总刚度矩阵凝缩到接触边界，形成关于接触内⼒的柔度⽅程，⼤⼤缩短了计算时间。

⽽后，李润⽅、陈万吉、B .C. Lee等将接触问题的表⾯⾮线性和材料⾮线性相藕合。

提出了有摩擦的弹塑性接触有限元混合法。

T.An dersion等提出了⼆维弹性接触问题的边界元法，⽽后逐渐发展到三维接触问题、热弹性问题等。

这些研究成果为齿轮接触特性的数值分析提供了理论基础。

S. M. Vijayakar⽤弹性接触有限元法研究了斜齿轮、锥齿轮、蜗轮蜗杆的接触应⼒。

李润⽅等对轮齿接触特性作了深⼊的研究考虑了轮齿的弹塑性变形、齿⾯摩擦、本体温度等的影响，并对轮齿啮合过程作分析，给出了最佳齿廓修形曲线等重要结论。

C.Gosselin等⽤有限元法分析了直齿轮和锥齿轮接触区的位移和应⼒，并与解析解进⾏了⽐较，两者相差20%以上。

1.1弹性固体的Hertz接触理论in 模型简化及其条件为了计算局部的变形我们对接触模型引入一些简化•每个物体均看作一个弹性的半空间体•我荷作用于平表面上•表面间无靡擦，只传递法向压力按照这种简化，根据两物体中的一般应力分布由物体的形状及它们被支承的方式而引起。

此外，已经充分发展了的解决弹性半空间体边值问题的方法，对解决接触问题是有效的。

为使这种简化合理，必须满足如下两个条件：•接触区的有效尺寸远远小于物体的尺寸•接触区的有效尺寸远远小于相对曲率半径第一个条件显然是必要的，用以保证以无限延伸的物体为基础所计算的应力场，不因其边界靠近高应力区而受重大影响。

第二个条件也是必要的，首先，为了保证紧靠接触区外的表面兴体上近似于半空间的平表面：其次，为了保证夜触区的应变足够小，时期处于线弹性理论的范I韦1内。

当然，把该理论的结果应用于低弹件模最的材料时必须小心，比如橡皮，很容易产生超出小应变限制的变形。

我们假设表而是无摩擦的，因此在两表而之间只传递法向压力。

虽然从物理上讲接触压力必须垂直于作用面，而作用面不一定是平的，但是线弹性理论并不计及由于它们产生的变形所造成的边界力的改变。

因此，鉴于每个物体都理想化为具有一个平表面的半空间体，我们取作用面上法向力平行于Z轴作用。

1 1.2 非协调接触几何描述当两个为协调固体接触的时候，它们最初是在一个点上或一条线上接触。

我们在列出弹性力学问题的方程之前，对接触面做儿何学上的分析是必要的。

我们建立一个亿初始接触点为坐标原点的直角坐标系，建立接触的几何模型，如图1J所示。

在宏观尺度上，表面外形函数以及它的一阶和二阶导数在接触区都是连续的。

于是我们町以用如下形式的表达式来近似地表示原点附近的曲面召=Asr + B^y2 + QXV+ （11）通过选择x和y轴的方位，使得xy项消失，式（4 1）可写成：21 =扌（击* + 和2）（1.2a）式中的R和R是该曲而在原点的主曲率半径。

齿轮动态接触分析结果对比内容：对比分析APDL经典界面、命令流分析、理论计算的齿轮接触应力结果1.模型的几何尺寸两个齿轮的基本参数如表1，表2所示，其中齿厚为10mm，根据表中的数据可以计算出两个齿轮的中心距离为81mm。

表1.1大齿轮的基本参数表1.2小齿轮的基本参数2、单元的选择及材料常数用8节点SOLID185单元模拟齿轮，通过接触向导建立齿轮之间的接触对和齿轮的刚性约束，则接触单元和目标单元将自动分配，两个齿轮的材料均为45号钢。

3、边界条件主动齿轮，约束齿轮内缘的径向位移和轴向位移，大齿轮为被动齿轮约束径向位移和轴向位移。

模拟齿轮组工况为小齿轮均匀转速0.2rad/s，大齿轮承受1200N/m的阻力扭矩，计算时间为1s。

4、齿面接触应力图4.1直齿圆柱齿轮受力分析112/tan/costr tn tF T dF FF F==∂=∂载荷、齿面相对滑动方向、摩擦因数和润滑状态有关。

齿面接触应力中赫兹应力占主要部分，并以此应力为接触疲劳强度计算基础应力。

maxE=σ （ 式一）式中：Σρ--综合曲率半径，mm 。

121121sin cos sin ==212cos 1d d '''∂∂∂=••'±±∂±Σρρμμρρρμμ （式二）接触线长度与重合度有关，按式 计算：2=bL Z ε （式三）Z ε为接触疲劳强度计算的重合度系数，表达式为Z ε=（式四） 将综合半径和接触线长度代入（式一），同时引入载荷系数K H ,可得：[]H H E H E H Z Z Z Z Z εε=≤σσ 其中H Z --区域系数。

式中H σ、[]H σ的单位为MPa ，d 1的单位为mm 。

5、ansysAPDL 齿轮动态分析结果5.1时间历程后处理器通过时间历程后处理器我们可以将接触应力随着时间的变化值导出。

如图5.1时间历程后处理器所示图5.1时间历程后处理器5.2导出某一点的接触应力值选取某一单元节点，该点的的接触应力随时间的变化值如下所示：TIME ESOL CONTPRESCONTPRES_20.10000 0.000000.20000 0.000000.30000 0.000000.40000 0.000000.50000 0.000000.60000 0.000000.70000 0.000000.80000 0.000000.90000 0.000001.0000 0.000001.1000 0.000001.2000 0.000001.3000 0.000001.4000 0.000001.5000 0.000001.6000 0.000001.7000 0.000001.8000 0.000001.9000 0.000002.0000 0.000002.1000 0.000002.2000 0.000002.3000 0.000002.4000 0.000002.5000 0.142461E+0072.6000 0.884816E+0082.7000 0.176954E+0092.8000 0.263984E+0092.9000 0.349861E+0093.0000 0.434189E+0093.1000 0.522552E+0093.2000 0.608327E+0093.3000 0.653361E+0093.4000 0.701361E+0093.5000 0.748924E+0093.6000 0.794247E+0093.7000 0.842083E+0093.8000 0.888082E+0093.9000 0.935456E+0094.0000 0.983938E+0094.1000 0.102099E+0104.2000 0.104590E+0104.3000 0.107369E+0104.4000 0.110070E+0104.5000 0.113327E+0104.6000 0.115482E+0104.7000 0.117339E+0104.8000 0.119205E+0104.9000 0.120717E+0105.0000 0.121669E+0105.1000 0.122092E+0105.2000 0.122325E+0105.3000 0.122426E+0105.4000 0.122624E+0105.5000 0.122597E+0105.6000 0.122706E+0105.7000 0.122850E+0105.8000 0.123096E+0105.9000 0.123222E+0106.0000 0.123352E+010图5.2是某一单元节点的接触应力曲线图，从图中我们可以看出在6秒时，该点处的接触应力达到最大值为1233MPa。