ANSYS粘弹性材料Prony总结

在做粘弹性分析之前建议先看一些粘弹性理论方面的书籍，知道一些基本概念，在做粘弹性分析之前建议先看一些粘弹性理论方面的书籍，知道一些基本概念，ansys中粘弹性材料模型的参数可以直接指定，也可以通过蠕变或者松弛实验数据输入。

最终的参数是基本单元的数目，基本单元对应的迟豫时间，各单元的相对剪切模量，各单元的相对体积模量，初始剪切模量，初始泊松比。

以上是一位高人告诉我的,我也不是特别清楚,下面是一篇关于粘弹性模型的帖子,你看看吧转贴一篇大海之子和dengnch两位学兄写的帖子，原来发在有限元联盟，希望对你有帮助。

ANSYS中粘弹性材料的参数意义：我用的材料知道时温等效方程（W.L.F.方程），ANSYS 中的本构模型用MAXWELL模型表示。

１．活化能与理想气体常数的比值（Tool-Narayanaswamy Shift Function）或者时温方程的第一个常数。

２．一个常数当用Tool-Narayanaswamy Shift Function（这个方程我不懂）的方程描述，或者是时温方程第２个常数３．定义体积衰减函数的MAXWELL单元数（在时温方程中用不到）４．时温方程的参考温度５．决定１、２、３、４参数的值６－１５定义体积衰减函数的系数，１６－２５定义fictive temperature的松弛时间这２０个数最终用来定义fictive temperature（在理论手册中介绍，不用在时温方程中）２６－３０和３１－３５分别定义了材料在不同物理状态时的热扩散系数３６－４５用来定义fictive temperature的fictive temperature的一些插值一类的数值，时温方程也用不到４６剪切模量开始松弛的值４７松弛时间无穷大的剪切模量的值４８体积模量开始松弛的值４９松弛时间无穷大的体积模量的值５０描述剪切松弛模量的MAXWELL模型的单元数５１－６０拟合剪切松弛模量的prony级数的系数值６１－７０拟合剪切松弛模量的prony级数的指数系数值（形式参看理论手册）７１描述体积松弛模量的MAXWELL模型的单元数７６－８５拟合体积松弛模量的prony级数的系数值８５－９５拟合体积松弛模量的prony级数的指数系数值（形式参看理论手册）进入ansys非线性粘弹性材料有两项：（1）maxwell(麦克斯韦)模型前面大海之子兄弟介绍了，最多可以输入95个常数（2）prony(普朗尼）模型这个模型下面又有三项：（a)shear Responsea1: 即理论中的C1-Relative modulus: 相对剪切模量t1: 即理论中的C2-Relative time: 相对时间（b） Volumetric Response（容积响应）a1: 即理论中的C1-Relative modulus: 相对弹性模量t1: 即理论中的C2-Relative time: 相对时间（c） Shift function (转换函数)有三项可以选择：（I） William-Landel, ferry: 时温等效方程Tref: 即理论中的C1-Relative temperature: 相对温度（对应《粘弹性理论》中的时温等效方程（WFL方程）应该是玻璃化转变温度）C1,C2: 没有什么好说的了，就是WFL方程的常量，与材料有关；（II） Tool-Narayanaswamy 方程Tref: 即理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）C1: 没有什么好说的了，就是TN常量；（III）用户定义Tref: 即理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）C1: 没有什么好说的了，就是方程的常量；-------------------------------------------------------------------------我做的结构是夹层板壳结构，就是利用粘弹性材料剪切耗能，师兄用nastran计算的时候，对粘弹性材料，只输入了粘弹性材料的剪切模量，我认为至少没考虑温度，另外还有频率问题。

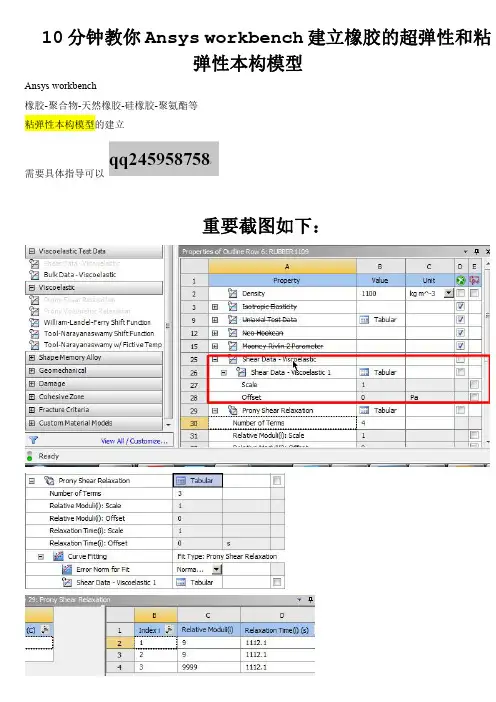
10分钟教你Ansys workbench建立橡胶的超弹性和粘弹性本构模型Ansys workbench橡胶-聚合物-天然橡胶-硅橡胶-聚氨酯等粘弹性本构模型的建立需要具体指导可以重要截图如下：补充：ANSYS 粘弹性材料1.1ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分，在载荷作用下弹性部分是即时响应的，而粘性部分需要经过一段时间才能表现出来。

一般的，应力函数是由积分形式给出的，在小应变理论下，各向同性的粘弹性本构方程可以写成如下形式：()()002t t de d G t d I K t d d d σττττττ∆=-+-⎰⎰(1)其中σ＝Cauchy 应力()G t ＝为剪切松弛核函数()K t ＝为体积松弛核函数e ＝为应变偏量部分（剪切变形）∆＝为应变体积部分（体积变形）t ＝当前时间τ＝过去时间I ＝为单位张量。

该式是根据松弛条件本构方程(1)，通过将一点的应变分解为应变球张量（体积变形）和应变斜张量（剪切变形）两部分，推导而得的。

这里不再敖述，可参考相关文献等。

ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种，一种是广义Maxwell 单元（VISCO88和VISCO89）所采用的Maxwell 形式，一种是结构单元所采用的Prony 级数形式。

实际上，这两种表示方式是一致的，只是具体数学表达式有一点点不同。

1.2Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为：()1exp G n i G i i t G t G G τ∞=⎛⎫=+- ⎪⎝⎭∑(2)()1exp K n i K i i t K t K K τ∞=⎛⎫=+- ⎪⎝⎭∑(3)其中，G ∞和i G 是剪切模量，K ∞和i K 是体积模量，G i τ和K i τ是各Prony 级数分量的松弛时间(Relative time)。

再定义下面相对模量(Relative modulus)0G i i G G α=(4)0K i i K K α=(5)其中，0G ，0K 分别为粘弹性材质的瞬态模量，并定义式如下：()010G n i i G G t G G ∞====+∑(6)()010Kn i i K K t K K ∞====+∑(7)在ANSYS 中，Prony 级数的阶数G n 和K n 可以不必相同，当然其中的松弛时间G i τ和K i τ也不必相同。

A N S Y S常用材料弹性模量及泊松比摩擦系数CAE常用材料弹性模量及泊松比摩擦系数摩擦系数━━━━━━━━━━━━━━━━━━━━━━━━摩擦副材料摩擦系数μ无润滑有润滑────────────────────────钢-钢 0.15* 0.1-0.12*0.1 0.05-0.1钢-软钢 0.2 0.1-0.2钢-不淬火的T8 0.15 0.03钢-铸铁 0.2-0.3* 0.05-0.150.16-0.18钢-黄铜 0.19 0.03钢-青铜 0.15-0.18 0.1-0.15*0.07钢-铝 0.17 0.02钢-轴承合金 0.2 0.04钢-夹布胶木 0.22 -钢-钢纸 0.22 -钢-冰 0.027* -0.014石棉基材料-铸铁或钢 0.25-0.40 0.08-0.12皮革-铸铁或钢 0.30-0.50 0.12-0.15材料(硬木)-铸铁或钢 0.20-0.35 0.12-0.16 软木-铸铁或钢 0.30-0.50 0.15-0.25钢纸-铸铁或钢 0.30-0.50 0.12-0.17毛毡-铸铁或钢 0.22 0.18软钢-铸铁 0.2*,0.18 0.05-0.15软钢-青铜 0.2*,0.18 0.07-0.15铸铁-铸铁 0.15 0.15-0.160.07-0.12铸铁-青铜 0.28* 0.16*0.15-0.21 0.07-0.15铸铁-皮革 0.55*,0.28 0.15*,0.12铸铁-橡皮 0.8 0.5皮革-木料 0.4-0.5* -0.03-0.05铜-T8钢 0.15 0.03铜-铜 0.20 -黄铜-不淬火的T8钢 0.19 0.03黄铜-淬火的T8钢 0.14 0.02黄铜-黄铜 0.17 0.02黄铜-钢 0.30 0.02黄铜-硬橡胶 0.25 -黄铜-石板 0.25 -黄铜-绝缘物 0.27 -青铜-不淬火的T8钢 0.16 -青铜-黄铜 0.16 -青铜-青铜 0.15-0.20 0.04-0.10 青铜-钢 0.16 -青铜-夹布胶木 0.23 -青铜-钢纸 0.24 -青铜-树脂 0.21 -青铜-硬橡胶 0.36 -青铜-石板 0.33 -青铜-绝缘物 0.26 -铝-不淬火的T8钢 0.18 0.03 铝-淬火的T8钢 0.17 0.02铝-黄铜 0.27 0.02铝-青铜 0.22 -铝-钢 0.30 0.02铝-夹布胶木 0.26 -硅铝合金-夹布胶木 0.34 -硅铝合金-钢纸 0.32 -硅铝合金-树脂 0.28 -硅铝合金-硬橡胶 0.25 -硅铝合金-石板 0.26 -硅铝合金-绝缘物 0.26 -钢-粉末冶金 0.35-0.55* -木材-木材 0.4-0.6* 0.1*0.2-0.5 0.07-0.10麻绳-木材 0.5-0.8* -0.545号淬火钢-聚甲醛 0.46 0.01645号淬火钢-聚碳酸脂 0.30 0.0345号淬火钢-尼龙9(加 0.57 0.023%MoS2填充料)45号淬火钢-尼龙9(加 0.48 0.02330%玻璃纤维填充物)45号淬火钢-尼龙1010 0.039 -(加30%玻璃纤维填充物)45号淬火钢-尼龙1010 0.07 -(加40%玻璃纤维填充物)45号淬火钢-氯化聚醚 0.35 0.03445号淬火钢-苯乙烯 0.35-0.46 0.018-丁二烯-丙烯腈共聚体(ABS)━━━━━━━━━━━━━━━━━━━━━━━━注:1.表中滑动摩擦系数是试验数值,只能作为近似计算参考.2.表中带"*"者为静摩擦系数.各种工程用塑料的摩擦系数━━━━━━━━━━━━━━━━━━━━━━━━━━下试样上试样(钢) 上试样(塑料)静摩擦动摩擦静摩擦动摩擦(塑料) 系数μs系数μk系数μs系数μk──────────────────────────聚四氟乙烯 0.10 0.05 0.04 0.04聚全氟乙丙烯 0.25 0.18 - -低密度聚乙烯 0.27 0.26 0.33 0.33高密度聚乙烯 0.18 0.08-0.12 0.12 0.11聚甲醛 0.14 0.13 - -聚偏二氟乙烯 0.33 0.25 - -聚碳酸酯 0.60 0.53 - -聚苯二甲酸乙 0.29 0.28 0.27* 0.20*二醇酯聚酰胺(尼龙66) 0.37 0.34 0.42* 0.35*聚三氟氯乙烯 0.45* 0.33* 0.43* 0.32*聚氯乙烯 0.45* 0.40* 0.50* 0.40*聚偏二氯乙烯 0.68* 0.45* 0.90* 0.52*━━━━━━━━━━━━━━━━━━━━━━━━━━注:*表示粘滑运动.常用材料的滚动摩擦系数━━━━━━━━━━━━━━━━━━━━摩擦副材料滚动摩擦系数 k,cm────────────────────淬火钢-淬火钢 0.001铸铁-铸铁 0.05木材-钢 0.03-0.04木材-木材 0.05-0.08铁或钢质车轮-木面 0.15-0.25钢质车轮-钢轨 0.05━━━━━━━━━━━━━━━━━━━━注:表中滚动摩擦系数是试验值,只能作近似参考.材料弹性模量及泊松比━━━━━━━━━━━━━━━━━━━━━━━━━名称弹性模量 E 切变模量 G 泊松比μGPa GPa─────────────────────────镍铬钢 206 79.38 0.25-0.30合金钢 206 79.38 0.25-0.30碳钢 196-206 79 0.24-0.28铸钢 172-202 0.3球墨铸铁 140-154 73-76 0.23-0.27灰铸铁 113-157 44 0.23-0.27白口铸铁 113-157 44 0.23-0.27冷拔纯铜 127 48轧制磷青铜 113 41 0.32-0.35轧制纯铜 108 39 0.31-0.34轧制锰青铜 108 39 0.35铸铝青铜 103 41冷拔黄铜 89-97 34-36 0.32-0.42轧制锌 82 31 0.27硬铝合金 70 26轧制铝 68 25-26 0.32-0.36 铅 17 7 0.42玻璃 55 22 0.25混凝土 14-23 4.9-15.7 0.1-0.18 纵纹木材 9.8-12 0.5横纹木材 0.5-0.98 0.44-0.64橡胶 0.00784 0.47电木 1.96-2.94 0.69-2.06 0.35-0.38 尼龙 28.3 10.1 0.4可锻铸铁 152拔制铝线 69大理石 55花岗石 48石灰石 41尼龙1010 10.7夹布酚醛塑料 4-8.8石棉酚醛塑料 1.3高压聚乙烯 0.15-0.25低压聚乙烯 0.49-0.78聚丙烯 1.32-1.42。

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:•什么是塑性•塑性理论简介•ANSYS程序中所用的性选项•怎样使用塑性•塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

ANSYS弹性及塑性（详细、全⾯）1讲解⽬录什么是塑性 (1)路径相关性 (1)率相关性 (1)⼯程应⼒、应变与真实应⼒、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使⽤塑性 (6)ANSYS输⼊ (7)输出量 (7)程序使⽤中的⼀些基本原则 (8)加强收敛性的⽅法 (8)查看结果 (9)塑性分析实例（GUI⽅法） (9)塑性分析实例（命令流⽅法） (14)弹塑性分析在这⼀册中,我们将详细地介绍由于塑性变性引起的⾮线性问题--弹塑性分析,我们的介绍⼈为以下⼏个⽅⾯:什么是塑性塑性理论简介ANSYS程序中所⽤的性选项怎样使⽤塑性塑性分析练习题什么是塑性塑性是⼀种在某种给定载荷下,材料产⽣永久变形的材料特性,对⼤多的⼯程材料来说,当其应⼒低于⽐例极限时,应⼒⼀应变关系是线性的。

另外,⼤多数材料在其应⼒低于屈服点时，表现为弹性⾏为，也就是说，当移⾛载荷时，其应变也完全消失。

由于屈服点和⽐例极限相差很⼩，因此在ANSYS程序中，假定它们相同。

在应⼒⼀应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类⾮线性问题叫作与路径相关的或⾮保守的⾮线性。

路径相关性是指对⼀种给定的边界条件，可能有多个正确的解—内部的应⼒，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的⼤⼩可能是加载速度快慢的函数，如果塑性应变的⼤⼩与时间有关，这种塑性叫作率⽆关性塑性，相反，与应变率有关的性叫作率相关的塑性。

⼤多的材料都有某种程度上的率相关性，但在⼤多数静⼒分析所经历的应变率范围，两者的应⼒－应变曲线差别不⼤，所以在⼀般的分析中，我们变为是与率⽆关的。

⼯程应⼒，应变与真实的应⼒、应变：塑性材料的数据⼀般以拉伸的应⼒—应变曲线形式给出。

粘弹性人工边界应用中的几个关键问题及其在ANSYS 中的实现蒋伟河海大学土木工程学院，江苏南京 (210098)E-mail: jw800403@摘 要：粘弹性人工边界能同时模拟半无限地基的能量辐射效应和弹性恢复能力，精度较高，计算结果稳定，在工程中受到越来越广泛的应用。

本文通过粘弹性人工边界理论，比较全面地介绍了粘弹性人工边界应用中人工边界的设置、参数选取、波动输入方法等几个关键问题以及在通用有限元分析软件ANSYS 中的实现，并结合平面问题算例，验证了该方法的有效性和准确性。

关键词：粘弹性人工边界；结构-地基动力相互作用；ANSYS ；波动输入1. 引言半无限地基的模拟问题是结构-地基动力相互作用分析中的一个关键问题。

目前通常的做法是在截取的有限域截断面上设置人工边界，合理地设置人工边界对于正确反映结构-地基的整体动力特性很重要。

人工边界大致可分为全局人工边界和局部人工边界两大类。

局部人工边界与全局人工边界相比，具有所需计算机存储量小、计算时间短、实用性强等优点，因此在实际工程中得到了比较广泛的应用。

局部人工边界中，工程上目前较常用的有廖振鹏等提出的透射边界[1]、Lysmer 等提出的粘性边界[2]，以及Deeks 在粘性边界的基础上提出了粘弹性人工边界[3]等。

透射边界虽具有较高精度，但在实际应用中一般仅限于二阶精度以内，并且存在编程较复杂、计算中可能引起高频失稳等问题。

粘性边界虽只有一阶精度，但概念清楚，易于程序实现，所以应用比较广泛，但其仅考虑了对散射波的吸收，不能模拟半无限地基的弹性恢复能力。

粘弹性边界具有能同时模拟散射波辐射和半无限地基的弹性恢复能力的优点，且能克服粘性边界引起的低频漂移问题，稳定性好。

目前，粘弹性人工边界已经开始应用到实际工程中，并越来越受到工程界的重视。

本文将以二维平面问题结合大型通用有限元计算软件ANSYS ，就粘弹性人工边界如何实现的几个问题做一简要的介绍。

ANSYS中粘弹性材料的参数意义：我用的材料知道时温等效方程（W.L.F.方程），ANSYS 中的本构模型用MAXWELL模型表示。

１．活化能与理想气体常数的比值（Tool-Narayanaswamy Shift Function）或者时温方程的第一个常数。

２．一个常数当用Tool-Narayanaswamy Shift Function的方程描述，或者是时温方程第２个常数３．定义体积衰减函数的MAXWELL单元数（在时温方程中用不到）４．时温方程的参考温度５．决定１、２、３、４参数的值６－１５定义体积衰减函数的系数，１６－２５定义fictive temperature的松弛时间这２０个数最终用来定义fictive temperature（在理论手册中介绍，不用在时温方程中）２６－３０和３１－３５分别定义了材料在不同物理状态时的热扩散系数３６－４５用来定义fictive temperature的fictive temperature的一些插值一类的数值，时温方程也用不到４６剪切模量开始松弛的值４７松弛时间无穷大的剪切模量的值４８体积模量开始松弛的值４９松弛时间无穷大的体积模量的值５０描述剪切松弛模量的MAXWELL模型的单元数５１－６０拟合剪切松弛模量的prony级数的系数值６１－７０拟合剪切松弛模量的prony级数的指数系数值（形式参看理论手册）７１描述体积松弛模量的MAXWELL模型的单元数７６－８５拟合体积松弛模量的prony级数的系数值８５－９５拟合体积松弛模量的prony级数的指数系数值（形式参看理论手册）进入ansys非线性粘弹性材料有两项：（1）maxwell(麦克斯韦)模型最多可以输入95个常数（2）prony(普朗尼）模型这个模型下面又有三项：（a)shear Responsea1: 即理论中的C1-Relative modulus: 相对剪切模量t1: 即理论中的C2-Relative time: 相对时间（b）V olumetric Response（容积响应）a1: 即理论中的C1-Relative modulus: 相对弹性模量t1: 即理论中的C2-Relative time: 相对时间（c）Shift function (转换函数)有三项可以选择：（I）William-Landel, ferry: 时温等效方程Tref: 即理论中的C1-Relative temperature: 相对温度（对应《粘弹性理论》中的时温等效方程（WFL方程）应该是玻璃化转变温度）C1,C2: 没有什么好说的了，就是WFL方程的常量，与材料有关；（II）Tool-Narayanaswamy 方程Tref: 即理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）C1: 没有什么好说的了，就是TN常量；（III）用户定义Tref: 即理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）C1: 没有什么好说的了，就是方程的常量；-------------------------------------------------------------------------《粘弹性理论》TB, Lab, MAT, NTEMP, NPTS, TBOPT, EOSOPT如果Lab:MATMaterial reference number (defaults to 1; maximum equals 100,000).NTEMP:Number of temperatures for which data will be provided. Default = 1; Max = 6.NPTS:Number of pairs of Prony series. Default = 1 pair; Max = 6 pairs.TBOPT:Defines the relaxation behavior for viscoelasticity.1--(or SHEAR) relaxation behavior of the shear response.2--(or BULK) relaxation behavior of the volumetric response.如果Lab:SHIFTNTEMP:Allows one temperature for which data will be provided.NPTS:Number of material constants to be entered as determined by the shift function specified by3--for TBOPT = WLF2--TBOPT = TNTBOPT:Defines the shift function1--( or WLF) William-Landel-Ferry shift function.2--(or TN) Tool-Narayanaswamy shift function.100--(or USER) User-defined shift function。

首先想要澄清一下粘弹性的概念，很多人认为粘弹性就是蠕变或者松弛，这不完全对。

描述粘弹性更为准确的方式应该叫做率依赖，就是本构方程中当时刻应力不仅与当时刻的应变有关，还与当时刻应变速率有关（如果还与以往的历史相关的话，就叫做粘弹塑性了）。

而蠕变与松弛只是当应力或者应变维持在定值的时候，产生的应变增加与应力减小的现象。

分清这个概念很重要，因为在abaqus中定义这些行为的方式是截然不同的，具体来说明一下粘弹性与蠕变（松弛）吧。

1粘弹性狭义上来讲粘弹性是材料在加载过程中应力变化与应变，应变率之间关系的描述，也可以称为率依赖问题。

如果你想要实现冲击载荷作用下粘弹性材料的反应，这个问题属于率依赖问题，你可以使用两种方法定义材料的力学响应，这就是微分型与积分性本构，虽然微分型本构比较直观明了，平衡方程也好获得，但是一般常用的还是基于遗传积分的积分性本构，毕竟微分型本构在基于时间或者频率离散的有限元方法中难于准确实现。

一般的粘弹性本构模型就那几个，比如maxwell，kelvin，剩下的就是它们的串联与并联，如果你有个新模型是n个maxwell串联的，你可以通过遗传积分公式轻易获得松弛模量与蠕变模量。

然而这里又会引出一个新的问题，学过粘弹性力学的人都知道，只要涉及到粘弹性问题势必逃不过一个数学工具——laplace变换,在这里不想多讲laplace变换的内容，大家对于这个数学工具应该都很清楚（如果是初学的话推荐两本书与粘弹性，laplace变化有关的教材，一个是周光泉的粘弹性理论，还有一本南京工学院，即东南大学出版的《积分变化这本书》），只谈谈它的物理意义吧，其实laplace变换的最核心思想在于时域与频域的转化，一个在时域内控制方程为偏微分方程的转化到频域内就是常微分方程了，对于粘弹性的松弛模量与蠕变模量也是这个道理，它存在着时域表示方法与频域表示方法。

它们在abaqus中的关键字为：*VISCOELASTIC, TIME= define1*VISCOELASTIC, FREQUENCY= d efine2其中define1，define2分别为数据定义方式，详细的可参考Abaqus Analysis User's Manual 18.7 Viscoelasticity。

1.粘弹性：ANSYS中的粘弹性模型是Maxwell模型的通用积分形式，其松弛函数由Prony级数表示。

该模型功能全面，Maxwell、Kevin和标准线性实体都是其特殊形式，全面支持亚粘弹性和大应变超粘弹性。

大应变超粘弹性基于Simo建议的列式，粘弹性行为的定义分为超弹性和松弛两个部分，所有的ANSYS超弹性材料模型都可采用粘弹性选项（PRONY）。

2. 粘弹性是率相关行为, 材料特性可能与时间和温度都有关，粘弹性响应可看作由弹性和粘性部分组成。

–弹性部分是可恢复的, 且是瞬时的。

–粘性部分是不可恢复的, 且在整个时间范围内发生。

ANSYS 中能模拟线性粘弹性，这导致如下假设:
–应变率与瞬态应力成比例
–瞬态应变与瞬态应力也成比例
–限于小应变、小变形行为(NLGEOM,OFF)
–
C5=1
FICT TEMP可以从帮助文件里找到
注意密度。

ANSYS中的泊松比NUXY和prxyANSYS中的泊松比NUXY和prxy横向应变与纵向应变之比值称为泊松比µ，也叫横向变性系数，它是反映材料横向变形的弹性常数。

在材料的比例极限内，由均匀分布的纵向应力所引起的横向应变与相应的纵向应变之比的绝对值。

比如，一杆受拉伸时，其轴向伸长伴随着横向收缩(反之亦然)，而横向应变e' 与轴向应变e 之比称为泊松比V。

材料的泊松比一般通过试验方法测定。

可以这样记忆：空气的泊松比为0，水的泊松比为0.5，中间的可以推出。

主次泊松比的区别Major and Minor Poisson's ratio主泊松比PRXY，指的是在单轴作用下，X方向的单位拉（或压）应变所引起的Y方向的压（或拉）应变次泊松比NUXY，它代表了与PRXY成正交方向的泊松比，指的是在单轴作用下，Y方向的单位拉（或压）应变所引起的X方向的压（或拉）应变。

PRXY与NUXY是有一定关系的：PRXY/NUXY=EX/EY对于正交各向异性材料，需要根据材料数据分别输入主次泊松比，但是对于各向同性材料来说，选择PRXY或NUXY来输入泊松比是没有任何区别的，只要输入其中一个即可简单推到如下：假如在单轴作用下：(1）X方向的单位拉（或压）应变所引起的Y方向的压（或拉）应变为b;（2）Y方向的单位拉（或压）应变所引起的X方向的压（或拉）应变为a;则根据胡克定律得σ=EX×a＝EY ×b→EX/EY ＝b／a又∵PRXY/NUXY＝b／a∴PRXY/NUXY=EX/EY1.在正交各项异性材料中才有PRXY和NUXY的概念，其实是PR??的下标与通常说的泊松比一致，而NU??的下标则相反，如下PRXY=Vxy,NUXY=Vyx为何有主(或大)泊松比和次(或小)泊松比之分呢?原来正交各项异性的刚度矩阵(或柔度矩阵)可以用12个工程常数决定，其中三个杨氏模量、六(三对)个泊松比和三个剪切模量。

ANSYS 粘弹性材料1.1 ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分，在载荷作用下弹性部分是即时响应的，而粘性部分需要经过一段时间才能表现出来。

一般的，应力函数是由积分形式给出的，在小应变理论下，各向同性的粘弹性本构方程可以写成如下形式：()()002t t de d G t d I K t d d d σττττττ∆=-+-⎰⎰ (1) 其中σ＝Cauchy 应力()G t ＝为剪切松弛核函数()K t ＝为体积松弛核函数e ＝为应变偏量部分（剪切变形）∆＝为应变体积部分（体积变形）t ＝当前时间τ＝过去时间I ＝为单位张量。

该式是根据松弛条件本构方程(1)，通过将一点的应变分解为应变球张量（体积变形）和应变斜张量（剪切变形）两部分，推导而得的。

这里不再敖述，可参考相关文献等。

ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种，一种是广义Maxwell 单元（VISCO88 和 VISCO89）所采用的Maxwell 形式，一种是结构单元所采用的Prony 级数形式。

实际上，这两种表示方式是一致的，只是具体数学表达式有一点点不同。

1.2 Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为：()1exp G n i G i it G t G G τ∞=⎛⎫=+- ⎪⎝⎭∑ (2) ()1exp K n i K i i t K t K K τ∞=⎛⎫=+- ⎪⎝⎭∑ (3) 其中，G ∞和i G 是剪切模量，K ∞和i K 是体积模量，G i τ和K i τ是各Prony 级数分量的松弛时间(Relative time)。

再定义下面相对模量(Relative modulus)0G i i G G α= (4)0K i i K K α= (5)其中，0G ，0K 分别为粘弹性材质的瞬态模量，并定义式如下：()010Gn i i G G t G G ∞====+∑ (6)()010Kn i i K K t K K ∞====+∑ (7)在ANSYS 中，Prony 级数的阶数G n 和K n 可以不必相同，当然其中的松弛时间G i τ和Ki τ也不必相同。