当前位置：文档之家 › (完整版)ANSYS粘弹体分析

(完整版)ANSYS粘弹体分析

  • 格式：doc
  • 大小：493.51 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

CAE-ANSYS Mechanical介绍(超弹性、粘弹性)

CAE-ANSYS Mechanical介绍(超弹性、粘弹性)

应用多种超弹性本构的案例：膝盖韧带分析
Cartilage(软骨) Isotropic Mooney-Rivlin
Ligament(韧带) Transversely isotropic Neo-Hookean
Meniscus(半月板)
Fung
W
2
I1
3
F2 (I4 )
Orthotropic Hyperelastic:
i 1
2i
3 i
3
第三类分子统计学本构模型，Neo-Hookean、Gent。
W
2
I1
3
5
超弹性模型 介绍
6
超弹性模型 选择
• 2阶项的 Mooney-Rivlin模型（ANSYS提供2,3,5,9参数的 模型）
W C1I1 3 C2 I2 3
W C1(I1 3) C2 (I2 3) C3 (I1 3)(I2 3)
Cauchy应力 剪切松弛模量 Green应变
t
0
2G t
de
d
d
t
I 0
K
t
d
d
d
式中σ——Cauchy应力(真实应力)
G(t)——为剪切松弛核函数
K(t)——为体积松弛核函数(由于体积几乎不变，可不考虑)
e——为应变偏量部分(剪切变形)
Δ——为应变体积部分(体积变形)
t——当前时间
τ——过去时间
粘弹性模型 静态 时温等效
• 时温等效原理 升高温度与延长时间对分子运动或高聚物的粘弹行为都
是等效的，这个等效性可以借助转换因子aT，将在某一温度 下测定的力学数据转换成另一温度下的数据.
静态下，升高温度与延长时间等效 降低温度与缩短时间等效

ansys粘塑性分析-Anand模型

ansys粘塑性分析-Anand模型

式中
[ ( )] ε&cr
− C4
= C1e T
sinh
C2σ
C3
C1
=
A,
C2
=
ξ
s
,
C3
=
1, m
C4
=
Q R
双曲正弦蠕变方程和 Anand 模型的主要区别是演化方程 [变形 抗力(s)], 下面解释
演化方程(应变强化/软化)为:
式中
( ) s& = ⎪⎩⎪⎨⎧ho
B
a
B B
⎪⎭⎪⎬⎫ε&in
s t res s (e.g., psi, MPa) s t res s (e.g., psi, MPa)
dimensionless
dimensionless, a>1.0
所有常数必须为正的。
前面幻灯片所示的 Anand 模型的9个材料常 数可以通过命令或材料 GUI 定义(如下所示):
– 通过 TB,ANAND 定义 Anand 模型。
8
9
Pa ra m e te r De scription
so Q/R
A
initial value of deformation res is t anc e activation energy divided by universal gas constant pre-exponential factor
ANAND支持的单元
• 仅有三种单元类型支持Anand模型: VISCO106-108
– VISCO106-108 是基于惩罚的混合 U-P 单 元(参考本书第2章)。
• VISCO106 是低阶2D单元。 • VISCO107 是低阶3D单元。 • VISCO108 是高阶2D单元。

(完整版)ANSYS粘弹体分析

(完整版)ANSYS粘弹体分析

ANSYS 中粘弹材质属性参数输入和分析 (1)1.1 ANSYS 中表征粘弹性属性问题 ............................................................................................................... 1 1.2 Prony 级数形式 .......................................................................................................................................... 1 1.3 Maxwell 形式 .............................................................................................................................................. 3 1.3 建模与载荷条件 . (5)1.3.1 模型设计 .......................................................................................................................................... 5 1.3.2 有限元建模 ...................................................................................................................................... 5 1.3.3 理论解析解计算式 .......................................................................................................................... 6 1.4 有限元数值解与结果比较 . (6)1.4.1 Plane183，Prony 级数方式 ............................................................................................................. 6 1.4.5 算例结论 . (10)ANSYS 中粘弹材质属性参数输入和分析1.1 ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分，在载荷作用下弹性部分是即时响应的，而粘性部分需要经过一段时间才能表现出来。

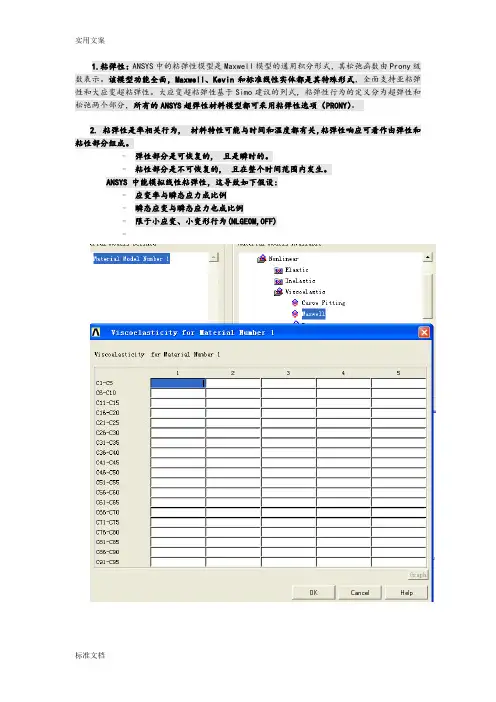
ansys粘弹性maxwell模型全参数总结材料

ansys粘弹性maxwell模型全参数总结材料

1.粘弹性：ANSYS中的粘弹性模型是Maxwell模型的通用积分形式，其松弛函数由Prony级数表示。

该模型功能全面，Maxwell、Kevin和标准线性实体都是其特殊形式，全面支持亚粘弹性和大应变超粘弹性。

大应变超粘弹性基于Simo建议的列式，粘弹性行为的定义分为超弹性和松弛两个部分，所有的ANSYS超弹性材料模型都可采用粘弹性选项（PRONY）。

2. 粘弹性是率相关行为, 材料特性可能与时间和温度都有关，粘弹性响应可看作由弹性和粘性部分组成。

–弹性部分是可恢复的, 且是瞬时的。

–粘性部分是不可恢复的, 且在整个时间范围内发生。

ANSYS 中能模拟线性粘弹性，这导致如下假设:
–应变率与瞬态应力成比例
–瞬态应变与瞬态应力也成比例
–限于小应变、小变形行为(NLGEOM,OFF)
–
C5=1
FICT TEMP可以从帮助文件里找到
注意密度。

ansys高级非线性分析五粘弹性

ansys高级非线性分析五粘弹性

& σ = SR (εin )σo
等效有效应力 应变率强化 [应力比率] (TB,RATE) 静态屈服应力 (TB,BISO/MISO/NLISO)
3
应力比率
ε &in m & SR (εin ) = 1+ γ & &in ) = 1+ εin SR (ε γ
m
PERZYNA
Perzyna 模型
2
1
PEIRCE
Peirce 模型
0 0 1 2 3 4 5
正则化应变率
September 30, 2001 Inventory #001491 5-8
粘塑性
... RATE 粘塑性选项
• 这意味着应力比率作为应变率的函数而改变。 这意味着应力比率作为应变率的函数而改变。
用 Perzyna 模型的例子
September 30, 2001 Inventory #001491 5-9
粘塑性
... RATE 粘塑性选项
• 关于 关于RATE模型的一些假设 模型的一些假设: 模型的一些假设
Training Manual
Advanced Structural Nonlinearities 6.0
September 30, 2001 Inventory #001491 5-3
粘塑性
... 粘塑性理论的背景
• ANSYS中率相关塑性模型的总结 中率相关塑性模型的总结: 中率相关塑性模型的总结
CREEP Behavior Isotropic or anisotropic creep (see HILL below) No explicitly defined yield surface RATE 1 Strain rate- or time-dependent Isotropic or anisotropic viscoplasticity (see HILL below) Includes yield surface ANAND Isotropic

ANSYS弹性及塑性（详细、全面）1讲解

ANSYS弹性及塑性（详细、全面）1讲解

ANSYS弹性及塑性（详细、全⾯）1讲解⽬录什么是塑性 (1)路径相关性 (1)率相关性 (1)⼯程应⼒、应变与真实应⼒、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使⽤塑性 (6)ANSYS输⼊ (7)输出量 (7)程序使⽤中的⼀些基本原则 (8)加强收敛性的⽅法 (8)查看结果 (9)塑性分析实例（GUI⽅法） (9)塑性分析实例（命令流⽅法） (14)弹塑性分析在这⼀册中,我们将详细地介绍由于塑性变性引起的⾮线性问题--弹塑性分析,我们的介绍⼈为以下⼏个⽅⾯:什么是塑性塑性理论简介ANSYS程序中所⽤的性选项怎样使⽤塑性塑性分析练习题什么是塑性塑性是⼀种在某种给定载荷下,材料产⽣永久变形的材料特性,对⼤多的⼯程材料来说,当其应⼒低于⽐例极限时,应⼒⼀应变关系是线性的。

另外,⼤多数材料在其应⼒低于屈服点时，表现为弹性⾏为，也就是说，当移⾛载荷时，其应变也完全消失。

由于屈服点和⽐例极限相差很⼩，因此在ANSYS程序中，假定它们相同。

在应⼒⼀应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类⾮线性问题叫作与路径相关的或⾮保守的⾮线性。

路径相关性是指对⼀种给定的边界条件，可能有多个正确的解—内部的应⼒，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的⼤⼩可能是加载速度快慢的函数，如果塑性应变的⼤⼩与时间有关，这种塑性叫作率⽆关性塑性，相反，与应变率有关的性叫作率相关的塑性。

⼤多的材料都有某种程度上的率相关性，但在⼤多数静⼒分析所经历的应变率范围，两者的应⼒－应变曲线差别不⼤，所以在⼀般的分析中，我们变为是与率⽆关的。

⼯程应⼒，应变与真实的应⼒、应变：塑性材料的数据⼀般以拉伸的应⼒—应变曲线形式给出。

ansys高级非线性分析五粘弹性

ansys高级非线性分析五粘弹性

粘塑性
A. 粘塑性背景
Training Manual
• 与前述的率无关塑性相反, 率相关塑性与应变速率或时间有关。从
材料的观点看, 粘塑性 和蠕变是相同的。
– 通常, 对工程用途, 蠕变用于描述在恒载荷下应变的变化。通常当温度 达到材料熔点的30-60%时, 蠕变变形就很重要，而且, 时间更长，蠕 变和塑性应变解耦。
Training Manual
记住首先定义线弹性材 料(EX 和 PRXY)。
否则, 当定义粘塑性时, 材料GUI将提示该信息。
第112页/共34页
Advanced Structural Nonlinearities 6.0
粘塑性
... 定义 RATE 材料特性
• 本例中选择了双线性等向强化的各向异性粘塑性。
• 当输入RATE常数后, 会出现率无关塑性参数对话框。
– 该例中, 输入双线性等向强化模型( BISO)的值, 即屈服应力和剪切模 量。
第143页/共34页
粘塑性
... 定义 RATE 材料特性
• 最后, 需要输入HILL参数来指定各向异性。
– 下面对话框中需要输入6个应力比率。
Training Manual
have different time scales
type problems
Temperature effects included as Can input temperature-dependent Anand's equation considers
part of equation (or material material constants, but equations do temperature effects directly. No

ANSYS弹性及塑性分析非常经典

ANSYS弹性及塑性分析非常经典

什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力.应变与真实应力.应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS 输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)査看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中，我们将详细地介绍由于塑性变性引起的非线性问题一弹塑性分析，我们的介绍人为以下几个方而：•什么是塑性•塑性理论简介•ANSYS程序中所用的性选项•怎样使用塑性•塑性分析练习题什么是塑性塑性是一种在某种给定载荷下，材料产生永久变形的材料特性，对大多的工程材料来说, 当其应力低于比例极限时，应力一应变关系是线性盹另外，大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说•当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假左它们相同。

在应力一应变的曲线中.低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给左的边界条件，可能有多个正确的解一内部的应力，应变分布一存在，为了得到真正正确的结果.我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力一应变曲线差别不大，所以在一般的分析中.我们变为是与率无关的• 工程应力，应变与真实的应力.应变：塑性材料的数据一般以拉伸的应力一应变曲线形式给出。

ANSYS弹性及塑性分析(详细、全面分析)1

ANSYS弹性及塑性分析(详细、全面分析)1

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:∙什么是塑性∙塑性理论简介∙ANSYS程序中所用的性选项∙怎样使用塑性∙塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

ansys高级非线性分析七粘弹性

ansys高级非线性分析七粘弹性

September 30, 2001 Inventory #001491 7-4
粘弹性
... 粘弹性理论背景
Training Manual
Advanced Structural Nonlinearities 6.0
• 粘弹性是率相关行为 材料特性可能与时间和温度都有关，粘弹性 粘弹性是率相关行为, 响应可看作由弹性和粘性部分组成。 响应可看作由弹性和粘性部分组成。
响应
t
ε = constant
(plus delta function)
ε
←δ(t-to)
加载
t
响应
t
September 30, 2001 Inventory #001491 7-14
粘弹性
... Kelvin-Voigt 模型
• Kelvin-Voigt 模型有以下特征 模型有以下特征:
– 对蠕变 在外载作用下 应变是指数的并渐近至 σo/E 对蠕变, 在外载作用下,
– 首先定义一些常用的术语 – 通过使用一维流变模型来解释线性粘弹性行为，这将有助于说明广义 通过使用一维流变模型来解释线性粘弹性行为， Maxwell 模型的基本特征。 模型的基本特征。 – 使用所有粘弹性材料通用的一般输入要求。 使用所有粘弹性材料通用的一般输入要求。 – 焦点将转至 WLF 偏移函数和聚合物。 偏移函数和聚合物。 – 将他讨论 TN偏移函数及其对玻璃材料的适用性。 偏移函数及其对玻璃材料的适用性。 偏移函数及其对玻璃材料的适用性
η
September 30, 2001 Inventory #001491 7-11
粘弹性
... Maxwell 模型
• Maxwell模型是一个串联的弹簧和阻尼器。 模型是一个串联的弹簧和阻尼器。 模型是一个串联的弹簧和阻尼器 σ spring = σ dashpot

粘弹性边界-刘晶波-ansys中实现

粘弹性边界-刘晶波-ansys中实现

粘弹性人工边界在ANSYS中的实现作者：河海水妖 2007-11-07 00:25:58标签：知识/探索ansys粘弹性人工边界动力边界条件粘弹性人工边界在ANSYS中的实现从半空间无限域取一4X2的矩形平面结构，顶部中间一定范围内受随时间变化的均布荷载，荷载如下p(t)=t 当0< DIV>p(t)=2-t 当1<=t<=2时p(t)=0 当t>2时材料弹性模量E=2.5，泊松比0.25，密度1网格尺寸0.1X0.1，在网格边界上所有结点加法向和切向combin14号单元用以模拟粘弹性人工边界（有关理论可参考刘晶波老师的相关文章）。

combine14单元的两个结点，其中一个与实体单元相连，另一个结点固定。

网格图如图1所示时程分析的时间步长为0.02秒，共计算16秒。

计算得到四个控制点位移时程图如图2所示，控制点坐标A(0,2)、B(0,1)、C(0,0)、D(2,2).计算所用命令流如下：/PREP7L=4 !水平长度H=2 !竖起深度E=2.5 !弹性模量density=1 !密度nu=0.25 !泊松比dxyz=0.1 !网格尺寸G = E/(2.*(1.+nu)) !剪切模量alfa = E*(1-nu)/((1.+nu)*(1.-2.*nu)) !若计算平面应力，此式需要修改 Cp=sqrt(alfa/density) !压缩波速Cs=sqrt(g/density) !剪切波速R=sqrt(L*L/4.+H*H/4.) !波源到边界点等效长度KbT=0.5*G/R*dxyzKbN=1.0*G/R*dxyzCbT=density*Cs*dxyzCbN=density*Cp*dxyzET, 1, plane42,,,2 !按平面应变计算et, 2, combin14, ,, 2 !切向et, 3, combin14, ,, 2 !法向r, 2, KbT, CbTr, 3, KbN, CbNMP, EX, 1, EMP, PRXY, 1, nuMP, DENS, 1, densityrectng,-L/2.,L/2,0.,Hasel, allaesize, all, dxyzmshape,0,2Dmshkey,1amesh, all!以下建立底边界法向和切向弹簧阻尼单元nsel,s,loc,y,0.*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,1,npnpnum=node((ip-1)*dxyz-L/2.,0.,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x.,y-dxyz/2,z !定义底边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x-dxyz/2.,y,z !定义底边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddo!以下建立左边界法向和切向弹簧阻尼单元nsel,s,loc,x,-L/2*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,2,np !侧边界最下面一个点按底边界上处理npnum=node(-L/2,(ip-1)*dxyz,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x-dxyz/2.,y,z !定义左边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x,y-dxyz/2.,z !定义左边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddo!以下建立右边界法向和切向弹簧阻尼单元nsel,s,loc,x,L/2*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,2,np !侧边界最下面一个点按底边界上处理npnum=node(L/2,(ip-1)*dxyz,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x+dxyz/2.,y,z !定义右边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x,y-dxyz/2.,z !定义右边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddoallsel,all/pnum,type,1/number,1eplotfinish/soluANTYPE,trans!*TRNOPT,FULLLUMPM,0btime=0.02etime=16.00dtime=0.02*DO,itime,btime,etime,dtimeTIME,itimensel,s,loc,y,H !选中需要加荷载的点nsel,r,loc,x,-L/4,L/4*if,itime,lt,1.,thenf,all,fy,1*itime*elseif,itime,ge,1.0,and,itime,le,2.0f,all,fy,1*(2-itime)*elsef,all,fy,0.0*endifallsel,allSOLVE*ENDDO另外，还用自己编写的有限元程序计算了一下这个例子，并与ANSYS得到的结果进行了比较，结果非常吻合，这里给出A点的比较结果。

ANSYS中粘弹性材料的参数意义

ANSYS中粘弹性材料的参数意义

ANSYS中粘弹性材料的参数意义：我用的材料知道时温等效方程（W.L.F.方程），ANSYS 中的本构模型用MAXWELL模型表示。

１．活化能与理想气体常数的比值（Tool-Narayanaswamy Shift Function）或者时温方程的第一个常数。

２．一个常数当用Tool-Narayanaswamy Shift Function的方程描述，或者是时温方程第２个常数３．定义体积衰减函数的MAXWELL单元数（在时温方程中用不到）４．时温方程的参考温度５．决定１、２、３、４参数的值６－１５定义体积衰减函数的系数，１６－２５定义fictive temperature的松弛时间这２０个数最终用来定义fictive temperature（在理论手册中介绍，不用在时温方程中）２６－３０和３１－３５分别定义了材料在不同物理状态时的热扩散系数３６－４５用来定义fictive temperature的fictive temperature的一些插值一类的数值，时温方程也用不到４６剪切模量开始松弛的值４７松弛时间无穷大的剪切模量的值４８体积模量开始松弛的值４９松弛时间无穷大的体积模量的值５０描述剪切松弛模量的MAXWELL模型的单元数５１－６０拟合剪切松弛模量的prony级数的系数值６１－７０拟合剪切松弛模量的prony级数的指数系数值（形式参看理论手册）７１描述体积松弛模量的MAXWELL模型的单元数７６－８５拟合体积松弛模量的prony级数的系数值８５－９５拟合体积松弛模量的prony级数的指数系数值（形式参看理论手册）进入ansys非线性粘弹性材料有两项：（1）maxwell(麦克斯韦)模型最多可以输入95个常数（2）prony(普朗尼）模型这个模型下面又有三项：（a)shear Responsea1: 即理论中的C1-Relative modulus: 相对剪切模量t1: 即理论中的C2-Relative time: 相对时间（b）V olumetric Response（容积响应）a1: 即理论中的C1-Relative modulus: 相对弹性模量t1: 即理论中的C2-Relative time: 相对时间（c）Shift function (转换函数)有三项可以选择：（I）William-Landel, ferry: 时温等效方程Tref: 即理论中的C1-Relative temperature: 相对温度（对应《粘弹性理论》中的时温等效方程（WFL方程）应该是玻璃化转变温度）C1,C2: 没有什么好说的了，就是WFL方程的常量，与材料有关；（II）Tool-Narayanaswamy 方程Tref: 即理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）C1: 没有什么好说的了，就是TN常量；（III）用户定义Tref: 即理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）C1: 没有什么好说的了，就是方程的常量；-------------------------------------------------------------------------《粘弹性理论》TB, Lab, MAT, NTEMP, NPTS, TBOPT, EOSOPT如果Lab:MATMaterial reference number (defaults to 1; maximum equals 100,000).NTEMP:Number of temperatures for which data will be provided. Default = 1; Max = 6.NPTS:Number of pairs of Prony series. Default = 1 pair; Max = 6 pairs.TBOPT:Defines the relaxation behavior for viscoelasticity.1--(or SHEAR) relaxation behavior of the shear response.2--(or BULK) relaxation behavior of the volumetric response.如果Lab:SHIFTNTEMP:Allows one temperature for which data will be provided.NPTS:Number of material constants to be entered as determined by the shift function specified by3--for TBOPT = WLF2--TBOPT = TNTBOPT:Defines the shift function1--( or WLF) William-Landel-Ferry shift function.2--(or TN) Tool-Narayanaswamy shift function.100--(or USER) User-defined shift function。

ansys高级非线性分析七粘弹性 共41页

ansys高级非线性分析七粘弹性 共41页

粘弹性
B. 流变模型
Training Manual
• 在详细讨论 ANSYS 中可用的粘弹性选项之前, 对一些常用的流变 模型(1-D)进行总结有助于理解粘弹性行为。
• 下面的讨论依赖于两个基本模型, 弹簧和缓冲器
– 弹簧采用 Hooke 定律作为应力和应变的关系，这代表弹性固体。
s
E
– 缓冲器(或阻尼器)定义应力和应变率间的行为, 用于表示粘性流体。
– Maxwell 模型充分地描述了应力松弛而不是蠕变。 – Kelvin-Voigt 模型充分地描述了蠕变而不是应力松弛。 – SLM 提供了一个简单的蠕变和松弛行为的表示法。
• 速率效应如下:
– 快速加载极限: sE0E1e – 缓慢加载极限: sE0e
September 30, 2001 Inventory #001491 7-17
– 这是一些高阶单元(能使用退化形式)，虽然可能, 但不推荐用它们作为 低阶单元(减去中间节点)。
– 目前 2D 平面应力、壳和梁单元对粘弹性不可用。 – VISCO88/89 单元有应力刚化能力, 但假设为小应变、小位移行为。
September 30, 2001 Inventory #001491 7-19
Advanced Structural Nonlinearities 6.0
粘弹性
... 广义 Maxwell 模型
Training Manual
• 广义 Maxwell 模型是由k 个并联的弹簧 和缓冲器组成.
G0
G1
h1
k
s si i 0
s i

si i

G
i e
i

hi Gi

ANSYS中粘弹性材料及参数意义

ANSYS中粘弹性材料及参数意义

ANSYS中粘弹性材料的参数意义：我用的材料知道时温等效方程（W.L.F.方程），ANSYS 中的本构模型用MAXWELL模型表示。

１．活化能与理想气体常数的比值（Tool-Narayanaswamy Shift Function）或者时温方程的第一个常数。

２．一个常数当用Tool-Narayanaswamy Shift Function的方程描述，或者是时温方程第２个常数３．定义体积衰减函数的MAXWELL单元数（在时温方程中用不到）４．时温方程的参考温度５．决定１、２、３、４参数的值６－１５定义体积衰减函数的系数，１６－２５定义fictive temperature的松弛时间这２０个数最终用来定义fictive temperature（在理论手册中介绍，不用在时温方程中）２６－３０和３１－３５分别定义了材料在不同物理状态时的热扩散系数３６－４５用来定义fictive temperature的fictive temperature的一些插值一类的数值，时温方程也用不到４６剪切模量开始松弛的值４７松弛时间无穷大的剪切模量的值４８体积模量开始松弛的值４９松弛时间无穷大的体积模量的值５０描述剪切松弛模量的MAXWELL模型的单元数５１－６０拟合剪切松弛模量的prony级数的系数值６１－７０拟合剪切松弛模量的prony级数的指数系数值（形式参看理论手册）７１描述体积松弛模量的MAXWELL模型的单元数７６－８５拟合体积松弛模量的prony级数的系数值８５－９５拟合体积松弛模量的prony级数的指数系数值（形式参看理论手册）进入ansys非线性粘弹性材料有两项：（1）maxwell(麦克斯韦)模型最多可以输入95个常数（2）prony(普朗尼）模型这个模型下面又有三项：（a)shear Responsea1: 即理论中的C1-Relative modulus: 相对剪切模量t1: 即理论中的C2-Relative time: 相对时间（b）V olumetric Response（容积响应）a1: 即理论中的C1-Relative modulus: 相对弹性模量t1: 即理论中的C2-Relative time: 相对时间（c）Shift function (转换函数)有三项可以选择：（I）William-Landel, ferry: 时温等效方程Tref: 即理论中的C1-Relative temperature: 相对温度（对应《粘弹性理论》中的时温等效方程（WFL方程）应该是玻璃化转变温度）C1,C2: 没有什么好说的了，就是WFL方程的常量，与材料有关；（II）Tool-Narayanaswamy 方程Tref: 即理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）C1: 没有什么好说的了，就是TN常量；（III）用户定义Tref: 即理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）C1: 没有什么好说的了，就是方程的常量；-------------------------------------------------------------------------《粘弹性理论》TB, Lab, MAT, NTEMP, NPTS, TBOPT, EOSOPT如果Lab:MATMaterial reference number (defaults to 1; maximum equals 100,000).NTEMP:Number of temperatures for which data will be provided. Default = 1; Max = 6.NPTS:Number of pairs of Prony series. Default = 1 pair; Max = 6 pairs.TBOPT:Defines the relaxation behavior for viscoelasticity.1--(or SHEAR) relaxation behavior of the shear response.2--(or BULK) relaxation behavior of the volumetric response.如果Lab:SHIFTNTEMP:Allows one temperature for which data will be provided.NPTS:Number of material constants to be entered as determined by the shift function specified by3--for TBOPT = WLF2--TBOPT = TNTBOPT:Defines the shift function1--( or WLF) William-Landel-Ferry shift function.2--(or TN) Tool-Narayanaswamy shift function.100--(or USER) User-defined shift function。

利用ANSYS的曲线拟合功能模拟粘弹性材料

利用ANSYS的曲线拟合功能模拟粘弹性材料

利用 ANSYS 的曲线拟合功能模拟粘弹性材料
王甲勇，张争奇，栗培龙，武斌
长安大学，陕西西安（710064）
E-mail：jiayong.wang@
摘 要：为了实现对粘弹性材料的模拟，本文采用大型有限元软件 ANSYS 中自带的粘弹性 材料曲线拟合功能，用 prony 级数形式拟合剪切松弛模量和体积松弛模量，通过 APDL 参数 化语言实现动荷载的模拟，利用后处理分析动荷载作用下材料内部的第一、二、三以及 vonmiss 应力，得到变形发展图。证明了用其自带的曲线拟合功能模拟粘弹性的可能性，为 研究粘弹性材料和沥青混合料永久变形预估提供了一种用有限元直接模拟粘弹性材料简单 实用方法。 关键词：有限元，粘弹性，力学响应，Prony 级数
1. 引言
车辙是沥青混合料在高温时受荷载作用发生的剪切流动不可恢复变形,是路面常见的病 害之一，影响行车舒适性和安全性，并且车辙病害的处治很难，如何处治和预测车辙深度是 国内外的一个研究热点。
随着计算机和有限元技术的发展，研究人员开始用有限元技术来模拟沥青混合料，并取 得了丰厚的成果[1,2]。有限元提供给用户模拟粘弹性材料的模块[3,4]包括用于蠕变分析的蠕变 模块和 MAXWELL 模型模拟粘弹性模块以及自定义模块。使用最广泛的是蠕变模块和用户 自定义模块；其中蠕变模块是利用实验测的蠕变曲线进行回归拟和得到有限元中输入参数， 这会造成实验信息的遗漏，并只能用于静力分析；而用户自定义模块是建立在对材料本构关 系明确认识的基础上，要求用户确保开发程序的有效性，但目前并没成熟的粘弹性本构关系 理论。
∑ G (t)
=
G∞
+
nG i =1
Gi
exp
⎛ ⎜ ⎝
−
t

ANSYS弹性及塑性分析(详细、全面分析)1

ANSYS弹性及塑性分析(详细、全面分析)1
目
录
什么是塑 性…………………………………………………………………………1 路径相关 性………………………………………………………………………1 率相关 性…………………………………………………………………………1 工程应力、应变与真实应力、应 变……………………………………………1 什么是激活塑 性…………………………………………………………………2 塑性理论介 绍………………………………………………………………………2 屈服准 则…………………………………………………………………………2 流动准 则…………………………………………………………………………3 强化准 则…………………………………………………………………………3 塑性选 项……………………………………………………………………………5 怎样使用塑 性………………………………………………………………………6 ANSYS输 入…………………………………………………………………… 7 输出 量……………………………………………………………………………7 程序使用中的一些基本原 则……………………………………………………8 加强收敛性的方 法………………………………………………………………8 查看结 果…………………………………………………………………………9 塑性分析实例（GUI方法）
大。 流动准则： 流动准则描述了发生屈服时，塑性应变的方向，也就是说，流动准 则定义了单个塑性应变分量（， 等）随着屈服是怎样发展的。 一般来说，流动方程是塑性应变在垂直于屈服面的方向发展的屈服 准则中推导出来的。这种流动准则叫作相关流动准则，如果不用其它的 流动准 则（从其它不同的函数推导出来）。则叫作不相关的流动准 则。 强化准则： 强化准则描述了初始屈服准则随着塑性应变的增加是怎样发展的。 一般来说，屈服面的变化是以前应变历史的函数，在ANSYS程序 中，使用了两种强化准则。 等向强化是指屈服面以材料中所作塑性功的大小为基础在尺寸上扩 张。对Mises屈服准则来说，屈服面在所有方向均匀扩张。见图3-2。

ANSYS弹性及塑性分析1

ANSYS弹性及塑性分析1

什么是塑性⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1路径相关性⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1率相关性⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1工程应力、应变与真实应力、应变⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1什么是激活塑性⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2塑性理论介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2屈服准则⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2流动准则⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3强化准则⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3塑性选项⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5怎样使用塑性⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 ANSYS 输入⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7输出量⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7程序使用中的一些基本原则⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8加强收敛性的方法⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8查看结果⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9塑性分析实例（GUI 方法）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9塑性分析实例（命令流方法）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14弹塑性分析在这一册中 , 我们将详细地介绍由于塑性变性引起的非线性问题 -- 弹塑性分析 , 我们 的介绍人为以下几个方面 :什么是塑性 塑性理论简介ANSYS 程序中所用的性选项怎样使用塑性 塑性分析练习题什么是塑性塑性是一种在某种给定载荷下 , 材料产生永久变形的材料特性 ,对大多的工程材料来说 当其应力低于比例极限时 , 应力一应变关系是线性的 。

另外, 大多数材料在其应力低于屈服点 时，表现为弹性行为，也 就 是说，当 移 走 载 荷 时，其应变也完全消失。

粘弹性边界-刘晶波-ansys中实现

粘弹性边界-刘晶波-ansys中实现

粘弹性人工边界在ANSYS中的实现作者：河海水妖 2007-11-07 00:25:58标签：知识/探索ansys粘弹性人工边界动力边界条件粘弹性人工边界在ANSYS中的实现从半空间无限域取一4X2的矩形平面结构，顶部中间一定范围内受随时间变化的均布荷载，荷载如下p(t)=t 当0< DIV>p(t)=2-t 当1<=t<=2时p(t)=0 当t>2时材料弹性模量E=2.5，泊松比0.25，密度1网格尺寸0.1X0.1，在网格边界上所有结点加法向和切向combin14号单元用以模拟粘弹性人工边界（有关理论可参考刘晶波老师的相关文章）。

combine14单元的两个结点，其中一个与实体单元相连，另一个结点固定。

网格图如图1所示时程分析的时间步长为0.02秒，共计算16秒。

计算得到四个控制点位移时程图如图2所示，控制点坐标A(0,2)、B(0,1)、C(0,0)、D(2,2).计算所用命令流如下：/PREP7L=4 !水平长度H=2 !竖起深度E=2.5 !弹性模量density=1 !密度nu=0.25 !泊松比dxyz=0.1 !网格尺寸G = E/(2.*(1.+nu)) !剪切模量alfa = E*(1-nu)/((1.+nu)*(1.-2.*nu)) !若计算平面应力，此式需要修改 Cp=sqrt(alfa/density) !压缩波速Cs=sqrt(g/density) !剪切波速R=sqrt(L*L/4.+H*H/4.) !波源到边界点等效长度KbT=0.5*G/R*dxyzKbN=1.0*G/R*dxyzCbT=density*Cs*dxyzCbN=density*Cp*dxyzET, 1, plane42,,,2 !按平面应变计算et, 2, combin14, ,, 2 !切向et, 3, combin14, ,, 2 !法向r, 2, KbT, CbTr, 3, KbN, CbNMP, EX, 1, EMP, PRXY, 1, nuMP, DENS, 1, densityrectng,-L/2.,L/2,0.,Hasel, allaesize, all, dxyzmshape,0,2Dmshkey,1amesh, all!以下建立底边界法向和切向弹簧阻尼单元nsel,s,loc,y,0.*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,1,npnpnum=node((ip-1)*dxyz-L/2.,0.,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x.,y-dxyz/2,z !定义底边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x-dxyz/2.,y,z !定义底边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddo!以下建立左边界法向和切向弹簧阻尼单元nsel,s,loc,x,-L/2*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,2,np !侧边界最下面一个点按底边界上处理npnum=node(-L/2,(ip-1)*dxyz,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x-dxyz/2.,y,z !定义左边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x,y-dxyz/2.,z !定义左边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddo!以下建立右边界法向和切向弹簧阻尼单元nsel,s,loc,x,L/2*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,2,np !侧边界最下面一个点按底边界上处理npnum=node(L/2,(ip-1)*dxyz,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x+dxyz/2.,y,z !定义右边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x,y-dxyz/2.,z !定义右边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddoallsel,all/pnum,type,1/number,1eplotfinish/soluANTYPE,trans!*TRNOPT,FULLLUMPM,0btime=0.02etime=16.00dtime=0.02*DO,itime,btime,etime,dtimeTIME,itimensel,s,loc,y,H !选中需要加荷载的点nsel,r,loc,x,-L/4,L/4*if,itime,lt,1.,thenf,all,fy,1*itime*elseif,itime,ge,1.0,and,itime,le,2.0f,all,fy,1*(2-itime)*elsef,all,fy,0.0*endifallsel,allSOLVE*ENDDO另外，还用自己编写的有限元程序计算了一下这个例子，并与ANSYS得到的结果进行了比较，结果非常吻合，这里给出A点的比较结果。

ANSYS弹性及塑性分析(详细、全面分析)

ANSYS弹性及塑性分析(详细、全面分析)

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:•什么是塑性•塑性理论简介•ANSYS程序中所用的性选项•怎样使用塑性•塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ANSYS 中粘弹材质属性参数输入和分析 (1)1.1 ANSYS 中表征粘弹性属性问题 ............................................................................................................... 1 1.2 Prony 级数形式 .......................................................................................................................................... 1 1.3 Maxwell 形式 .............................................................................................................................................. 3 1.3 建模与载荷条件 . (5)1.3.1 模型设计 .......................................................................................................................................... 5 1.3.2 有限元建模 ...................................................................................................................................... 5 1.3.3 理论解析解计算式 .......................................................................................................................... 6 1.4 有限元数值解与结果比较 . (6)1.4.1 Plane183，Prony 级数方式 ............................................................................................................. 6 1.4.5 算例结论 . (10)ANSYS 中粘弹材质属性参数输入和分析1.1 ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分，在载荷作用下弹性部分是即时响应的，而粘性部分需要经过一段时间才能表现出来。

一般的，应力函数是由积分形式给出的，在小应变理论下，各向同性的粘弹性本构方程可以写成如下形式：()()002tt de d G t d I K t d d d σττττττ∆=-+-⎰⎰ (0.1)其中σ＝Cauchy 应力()G t ＝为剪切松弛核函数 ()K t ＝为体积松弛核函数 e ＝为应变偏量部分（剪切变形）∆＝为应变体积部分（体积变形）t ＝当前时间 τ＝过去时间 I ＝为单位张量。

该式是根据松弛条件本构方程(0.1)，通过将一点的应变分解为应变球张量（体积变形）和应变斜张量（剪切变形）两部分，推导而得的。

这里不再敖述，可参考相关文献等。

ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种，一种是广义Maxwell 单元（VISCO88 和 VISCO89）所采用的Maxwell 形式，一种是结构单元（如Plane183，Plane182等）所采用的Prony 级数形式。

实际上，这两种表示方式是一致的，只是具体数学表达式有一点点不同。

1.2 Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为：()1exp Gn i Gi itG t G G τ∞=⎛⎫=+- ⎪⎝⎭∑ (0.2)()1exp Kn i Ki itK t K K τ∞=⎛⎫=+- ⎪⎝⎭∑ (0.3) 其中，G ∞和i G 是剪切模量，K ∞和i K 是体积模量，Gi τ和Ki τ是各Prony 级数分量的松弛时间。

再定义下面相对模量0G i i G α= (0.4)0K i i K K α= (0.5)其中，0G ，0K 分别为粘弹性材质（固体推进剂）的瞬态模量，并定义式如下：()010Gn i i G G t G G ∞====+∑ (0.6)()010Kn i i K K t K K ∞====+∑ (0.7)在ANSYS 中，Prony 级数的阶数G n 和K n 可以不必相同，当然其中的松弛时间G i τ和Ki τ也不必相同。

对于粘弹性问题，粘弹体的泊松比一般是取为时间的函数()t μμ=。

不过有时情况允许也可近似设为常数，这时根据弹性常数关系就有：()()()()()()21312E t G t E t K t μμ=+=- (0.8)其中，()E t 为松弛模量，由实验来确定。

()()(),,E t G t K t 的相应系数比相同。

这样就可以将()G t 和()K t 统一于()E t 形式。

若我们将松弛模量表示为Prony 级数形式，即：()1exp n i i itE t E E τ∞=⎛⎫=+-⎪⎝⎭∑ (0.9) 于是，()G t 和()K t 中有，G K n n n ==，G Ki i i τττ==，G K i i i ααα==。

类似于0G 、0K ，我们也同样定义瞬态松弛模量0E ：()010Gn i i E E t E E ∞====+∑ (0.10)这样，由(0.8)可得()()00021312E G E K μμ=+=- (0.11)要注意的是，ANSYS 中对Prony 级数的支持项数不能超过6项，即6n ≤。

这确实是一个遗憾。

另外，――――――――――――――――――――――――――――――――――――――――――The viscoelasticity input for SHELL181, PLANE182, PLANE183, SOLID185, SOLID186, SOLID187, SOLSH190, SHELL208, and SHELL209 consists of elasticity properties and relaxation properties . The underlying elasticity is specified by either the MP command (for hypoelasticity) or by the TB ,HYPER command (for hyperelasticity). Use the TB ,PRONY or TB ,SHIFT commands to input the relaxation properties.―――――――――――――――――――――――――――――――――――――――――――――― 可见，此时除了由Prony 级数形式附加粘弹性，还需输入“弹性”属性。

这里我对hypoelasticity 不了解，具体也说不上来。

在ANSYS 帮助文档里有这样一段：――――――――――――――――――――――――――――――――――――――――――!Small Strain Viscoelasticitymp,ex,1,20.0E5 !elastic properties mp,nuxy,1,0.3tb,prony,1,,2,shear !define viscosity parameters (shear) tbdata,1,0.5,2.0,0.25,4.0 tb,prony,1,,2,bulk !define viscosity parameters (bulk) tbdata,1,0.5,2.0,0.25,4.0!Large Strain Viscoelasticity tb,hyper,1,,,moon !elastic properties tbdata,1,38.462E4,,1.2E-6tb,prony,1,,1,shear !define viscosity parameters tbdata,1,0.5,2.0 tb,prony,1,,1,bulk !define viscosity parameters tbdata,1,0.5,2.0―――――――――――――――――――――――――――――――――――――――――――1.3 Maxwell 形式――――――――――――――――――――――――――――――――――――――― For the viscoelastic elements VISCO88 and VISCO89 the material properties are expressed in integral form using the kernel function of the generalized Maxwell elements as:――――――――――――――――――――――――――――――――――――――()()11exp exp GKn i G i i n i K i i G G G K K K ξξλξξλ∞=∞=⎛⎫=+- ⎪⎝⎭⎛⎫=+- ⎪⎝⎭∑∑ (0.12)())00i i i iC G G GD K K K ∞∞=-=- (0.13)其中ξ为折算时间，由于不考虑温度载荷，方程中的折算时间就是实际时间，即t ξ=，类同Prony 级数情形的。

―――――――――――――――――――――――――――――――――――――――ξ = reduced or pseudo timeG(ξ) = shear relaxation kernel function K(ξ) = bulk relaxation kernel functionn G = number of Maxwell elements used to approximate the shear relaxation kernel (input constant 50) n K = number of Maxwell elements used to approximate the bulk relaxation kernel (input constant 71) C i = constants associated with the instantaneous response for shear behavior (input constants 51–60) D i = constants associated with the instantaneous response for bulk behavior (input constants 76–85) G 0 = initial shear modulus (input constant 46)G ∞= final shear modulus (input constant 47)K 0 = initial bulk modulus (input constant 48)K ∞ = final bulk modulus (input constant 49)G i λ = constants associated with a discrete relaxation spectrum in shear (input constant 61-70) K i λ= constants associated with a discrete relaxation spectrum in bulk (input constant 86-95)―――――――――――――――――――――――――同Prony 技术情形一样的： 由试验数据拟合得到(0.12)；由(0.12)即可确定：级数项数,G K n n ；K 和G 的初始值和稳态值：0,K K ∞和0,G G ∞；时间松弛系数Gi λ、Ki λ； 再分别根据(0.13)计算得到参数,i i C D 。