粘弹性人工边界在ANSYS中实现

粘弹性人工边界的有限元分析徐浩【摘要】采用数值方法集中比较了工程中广泛应用的几种人工边界在SSI体系分析中的动力反应,研究结果表明:粘性边界能较好的模拟土的边界但计算的位移会发生整体的飘逸,精度也不如粘弹性边界;粘弹性边界能很好的模拟土一结构相互作用体系中土的边界问题,但实现过程比较麻烦.【期刊名称】《山西建筑》【年(卷),期】2011(037)009【总页数】2页(P72-73)【关键词】人工边界;SSI体系;粘弹性人工边界;有限元法【作者】徐浩【作者单位】同济大学土木工程学院建筑工程系,上海,200092【正文语种】中文【中图分类】TU411土木工程中有许多涉及弹性半无限地基的振动及波动问题,诸如土—结构动力相互作用(SSI)问题、地震波的传播问题、动力机器基础的振动问题、打桩及道路交通引起的振动问题等。

对这类问题用有限元法求解与用其他计算方法相比具有可灵活地适用于地基物性的不均匀性并可考虑地基的非线性特性等优点。

但由于有限元法必须对求解对象的全领域进行离散,故在分析弹性半无限地基问题时必须截取一定范围的计算模型,这就要求在切取的边界上建立人工边界,用于模拟切除的无限域影响。

目前人工边界主要分为两类：一类是全局人工边界条件,如边界元法等;另一类是局部人工边界条件,如旁轴近似人工边界、透射人工边界、粘弹性人工边界等。

局部人工边界具有时空解耦的特点,得到了广泛的应用。

其中粘弹性人工边界是通过沿人工边界设置一系列由弹簧和阻尼器组成的简单物理元件来吸收射向人工边界的波动能量和反射波的散射,其模型简单,物理意义清晰,便于在大型通用有限元计算软件中得到实现。

ANSYS是一功能强大的有限元计算软件,其中的 ANSYS中的Combin14单元和 LSDYNA中的Combin165单元,是弹簧与阻尼器的元件,易于实现粘弹性人工边界。

本文在 ANSYS中实现了粘弹性边界并进行了验证和对比。

粘弹性人工边界作为一种应力边界条件,该应力是边界结点位移和速度的函数,一般形式写为：由式(1)可以看出,粘弹性边界相当于在边界结点每个方向施加一个一段固定的单向弹簧—阻尼元件,而且该弹簧—阻尼元件的刚度和阻尼系数仅与该边界结点在该方向该时刻的反应相关,从而通过粘性阻尼的吸能作用和弹簧的刚性恢复作用模拟无限域对广义结构的影响。

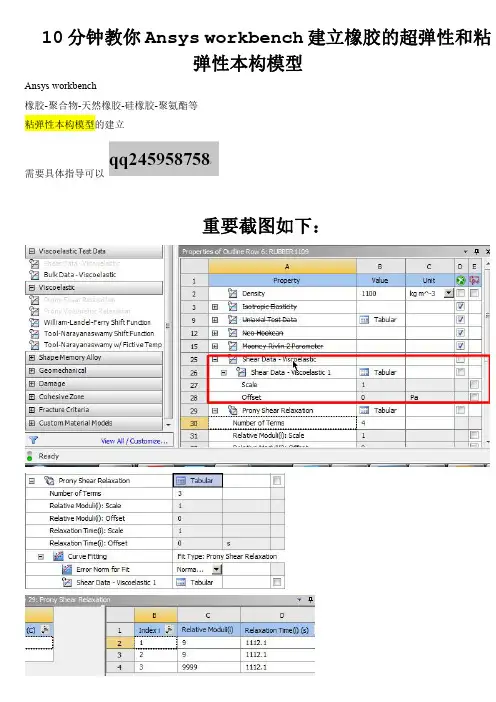
10分钟教你Ansys workbench建立橡胶的超弹性和粘弹性本构模型Ansys workbench橡胶-聚合物-天然橡胶-硅橡胶-聚氨酯等粘弹性本构模型的建立需要具体指导可以重要截图如下：补充：ANSYS 粘弹性材料1.1ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分，在载荷作用下弹性部分是即时响应的，而粘性部分需要经过一段时间才能表现出来。

一般的，应力函数是由积分形式给出的，在小应变理论下，各向同性的粘弹性本构方程可以写成如下形式：()()002t t de d G t d I K t d d d σττττττ∆=-+-⎰⎰(1)其中σ＝Cauchy 应力()G t ＝为剪切松弛核函数()K t ＝为体积松弛核函数e ＝为应变偏量部分（剪切变形）∆＝为应变体积部分（体积变形）t ＝当前时间τ＝过去时间I ＝为单位张量。

该式是根据松弛条件本构方程(1)，通过将一点的应变分解为应变球张量（体积变形）和应变斜张量（剪切变形）两部分，推导而得的。

这里不再敖述，可参考相关文献等。

ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种，一种是广义Maxwell 单元（VISCO88和VISCO89）所采用的Maxwell 形式，一种是结构单元所采用的Prony 级数形式。

实际上，这两种表示方式是一致的，只是具体数学表达式有一点点不同。

1.2Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为：()1exp G n i G i i t G t G G τ∞=⎛⎫=+- ⎪⎝⎭∑(2)()1exp K n i K i i t K t K K τ∞=⎛⎫=+- ⎪⎝⎭∑(3)其中，G ∞和i G 是剪切模量，K ∞和i K 是体积模量，G i τ和K i τ是各Prony 级数分量的松弛时间(Relative time)。

再定义下面相对模量(Relative modulus)0G i i G G α=(4)0K i i K K α=(5)其中，0G ，0K 分别为粘弹性材质的瞬态模量，并定义式如下：()010G n i i G G t G G ∞====+∑(6)()010Kn i i K K t K K ∞====+∑(7)在ANSYS 中，Prony 级数的阶数G n 和K n 可以不必相同，当然其中的松弛时间G i τ和K i τ也不必相同。

ansys 边界条件
ANSYS边界条件是指在ANSYS软件中给定模型的边界附加的限制条件，用于模拟真实世界中的物理现象。

通过添加边界条件，可以模拟出实际物理系统中的交互作用和约束条件，并且可以在ANSYS中计算出与这些条件相应的物理量。

在ANSYS中，边界条件可以被分为以下几种类型：
1. 几何边界条件：这种边界条件是指模型的几何形状或者物体表面自然的物理限制条件，如模型表面的固定支撑条件、物体的自由表面、周期性约束等。

2. 力和位移边界条件：这种边界条件是指在模型表面施加的力和位移条件，如加速度、质量、速度等。

3. 热边界条件：这种边界条件是指在模型表面施加的热约束条件，如导热系数、温度、热流量等。

4. 电磁边界条件：这种边界条件是指在电磁场中施加的电磁条件，如电场、磁场、电荷等。

在ANSYS中，可以通过界面和菜单来设置边界条件，也可以通过输入APDL命令来设置。

正确的边界条件设置可以使模拟结果更加准确，因此，在进行ANSYS仿真时，边界条件的设置是非常重要的一步。

- 1 -。

用ANSYS二次开发计算弹性-粘弹性复合结构的模态参数廖文冬;陈前
【期刊名称】《振动工程学报》
【年(卷),期】2004(017)0z2
【摘要】弹性-粘弹性复合结构目前在结构减振方面应用很广泛,但是现有的有限元分析软件系统尚不能有效地计算这种复合结构,因此本文将ANSYS进行二次开发,利用ANSYS进行前处理并计算出单元矩阵,再利用外挂程序进行模态计算,最后将结果返回ANSYS进行后处理.理论计算结果与实验结果进行比较,比较结果说明这种方法是可行的,计算精度满足要求.
【总页数】3页(P1074-1076)
【作者】廖文冬;陈前
【作者单位】南京航空航天大学航空宇航学院,南京,210016;南京航空航天大学航空宇航学院,南京,210016
【正文语种】中文
【中图分类】TB33;TB125
【相关文献】
1.弹性-粘弹性复合结构随机响应的各阶谱矩的计算方法 [J], 冉志;张天舒;方同
2.弹性-粘弹性复合板模态密度研究 [J], 王宏伟;赵德有
3.大型粘弹性复合结构的模态分析 [J], 刘曙远
4.附加粘弹性阻尼器结构模态阻尼比的计算 [J], 刘保东
5.弹性——粘弹性复合结构模态理论 [J], 陈前;朱德懋
因版权原因，仅展示原文概要，查看原文内容请购买。

粘弹性人工边界在ANSYS中的实现作者：河海水妖 2007-11-07 00:25:58标签：知识/探索ansys粘弹性人工边界动力边界条件粘弹性人工边界在ANSYS中的实现从半空间无限域取一4X2的矩形平面结构，顶部中间一定范围内受随时间变化的均布荷载，荷载如下p(t)=t 当0< DIV>p(t)=2-t 当1<=t<=2时p(t)=0 当t>2时材料弹性模量E=2.5，泊松比0.25，密度1网格尺寸0.1X0.1，在网格边界上所有结点加法向和切向combin14号单元用以模拟粘弹性人工边界（有关理论可参考刘晶波老师的相关文章）。

combine14单元的两个结点，其中一个与实体单元相连，另一个结点固定。

网格图如图1所示时程分析的时间步长为0.02秒，共计算16秒。

计算得到四个控制点位移时程图如图2所示，控制点坐标A(0,2)、B(0,1)、C(0,0)、D(2,2).计算所用命令流如下：/PREP7L=4 !水平长度H=2 !竖起深度E=2.5 !弹性模量density=1 !密度nu=0.25 !泊松比dxyz=0.1 !网格尺寸G = E/(2.*(1.+nu)) !剪切模量alfa = E*(1-nu)/((1.+nu)*(1.-2.*nu)) !若计算平面应力，此式需要修改 Cp=sqrt(alfa/density) !压缩波速Cs=sqrt(g/density) !剪切波速R=sqrt(L*L/4.+H*H/4.) !波源到边界点等效长度KbT=0.5*G/R*dxyzKbN=1.0*G/R*dxyzCbT=density*Cs*dxyzCbN=density*Cp*dxyzET, 1, plane42,,,2 !按平面应变计算et, 2, combin14, ,, 2 !切向et, 3, combin14, ,, 2 !法向r, 2, KbT, CbTr, 3, KbN, CbNMP, EX, 1, EMP, PRXY, 1, nuMP, DENS, 1, densityrectng,-L/2.,L/2,0.,Hasel, allaesize, all, dxyzmshape,0,2Dmshkey,1amesh, all!以下建立底边界法向和切向弹簧阻尼单元nsel,s,loc,y,0.*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,1,npnpnum=node((ip-1)*dxyz-L/2.,0.,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x.,y-dxyz/2,z !定义底边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x-dxyz/2.,y,z !定义底边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddo!以下建立左边界法向和切向弹簧阻尼单元nsel,s,loc,x,-L/2*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,2,np !侧边界最下面一个点按底边界上处理npnum=node(-L/2,(ip-1)*dxyz,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x-dxyz/2.,y,z !定义左边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x,y-dxyz/2.,z !定义左边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddo!以下建立右边界法向和切向弹簧阻尼单元nsel,s,loc,x,L/2*get,np,node,,count !得到选中的结点数，存入np*get,npmax,node,,num,maxd !得到已经定义的最大结点数，存入npmax*do,ip,2,np !侧边界最下面一个点按底边界上处理npnum=node(L/2,(ip-1)*dxyz,0.)x=nx(npnum)y=ny(npnum)z=nz(npnum)npmax=npmax+1n,npmax,x+dxyz/2.,y,z !定义右边界法向结点以便与边界点形成法向单元 type,3real,3e,npnum,npmaxd,npmax,all,0. !约束新生成的点npmax=npmax+1n,npmax,x,y-dxyz/2.,z !定义右边界切向结点以便与边界点形成切向单元 type,2real,2e,npnum,npmaxd,npmax,all,0. !约束新生成的点*enddoallsel,all/pnum,type,1/number,1eplotfinish/soluANTYPE,trans!*TRNOPT,FULLLUMPM,0btime=0.02etime=16.00dtime=0.02*DO,itime,btime,etime,dtimeTIME,itimensel,s,loc,y,H !选中需要加荷载的点nsel,r,loc,x,-L/4,L/4*if,itime,lt,1.,thenf,all,fy,1*itime*elseif,itime,ge,1.0,and,itime,le,2.0f,all,fy,1*(2-itime)*elsef,all,fy,0.0*endifallsel,allSOLVE*ENDDO另外，还用自己编写的有限元程序计算了一下这个例子，并与ANSYS得到的结果进行了比较，结果非常吻合，这里给出A点的比较结果。

粘弹性人工边界应用中的几个关键问题及其在ANSYS 中的实现蒋伟河海大学土木工程学院，江苏南京 (210098)E-mail: jw800403@摘 要：粘弹性人工边界能同时模拟半无限地基的能量辐射效应和弹性恢复能力，精度较高，计算结果稳定，在工程中受到越来越广泛的应用。

本文通过粘弹性人工边界理论，比较全面地介绍了粘弹性人工边界应用中人工边界的设置、参数选取、波动输入方法等几个关键问题以及在通用有限元分析软件ANSYS 中的实现，并结合平面问题算例，验证了该方法的有效性和准确性。

关键词：粘弹性人工边界；结构-地基动力相互作用；ANSYS ；波动输入1. 引言半无限地基的模拟问题是结构-地基动力相互作用分析中的一个关键问题。

目前通常的做法是在截取的有限域截断面上设置人工边界，合理地设置人工边界对于正确反映结构-地基的整体动力特性很重要。

人工边界大致可分为全局人工边界和局部人工边界两大类。

局部人工边界与全局人工边界相比，具有所需计算机存储量小、计算时间短、实用性强等优点，因此在实际工程中得到了比较广泛的应用。

局部人工边界中，工程上目前较常用的有廖振鹏等提出的透射边界[1]、Lysmer 等提出的粘性边界[2]，以及Deeks 在粘性边界的基础上提出了粘弹性人工边界[3]等。

透射边界虽具有较高精度，但在实际应用中一般仅限于二阶精度以内，并且存在编程较复杂、计算中可能引起高频失稳等问题。

粘性边界虽只有一阶精度，但概念清楚，易于程序实现，所以应用比较广泛，但其仅考虑了对散射波的吸收，不能模拟半无限地基的弹性恢复能力。

粘弹性边界具有能同时模拟散射波辐射和半无限地基的弹性恢复能力的优点，且能克服粘性边界引起的低频漂移问题，稳定性好。

目前，粘弹性人工边界已经开始应用到实际工程中，并越来越受到工程界的重视。

本文将以二维平面问题结合大型通用有限元计算软件ANSYS ，就粘弹性人工边界如何实现的几个问题做一简要的介绍。

粘弹性人工边界在有限元分析中的应用杜兴华;高扬【摘要】主要介绍了粘弹性人工边界的相关理论,牯弹性人工边界单元在ANSYS 中的具体实现方法,以及相关参数的计算公式.并且通过一个算例验证了粘弹性人工边界具有良好的计算精度和稳定性.【期刊名称】《低温建筑技术》【年(卷),期】2012(034)001【总页数】3页(P76-78)【关键词】粘弹性人工边界;ANSYS;地下结构【作者】杜兴华;高扬【作者单位】天津大学建筑工程学院,天津300072;天津大学建筑工程学院,天津300072【正文语种】中文【中图分类】TU471.2半无限地基的模拟是地下结构数值分析的一个关键问题。

目前普遍采用有限域来模拟半无限域，所以人工边界选取得是否合理，直接关系到数值分析的准确性。

目前较常用的有透射边界、粘性边界，粘弹性人工边界等。

透射边界虽具有较高精度，但编程较复杂、计算中可能引起高频失稳等问题［1］。

粘性边界概念清楚，易于程序实现，所以应用比较广泛，但其仅考虑了对散射波的吸收，不能模拟半无限地基的弹性恢复能力。

粘弹性边界具同时模拟散射波辐射和半无限地基的弹性恢复能力的优点，且能克服粘性边界引起的低频漂移问题，稳定性好。

目前，粘弹性人工边界已应用到实际工程中，并越来越受到工程界的重视。

1 粘弹性人工边界相关问题1.1 粘弹性人工边界理论粘弹性人工边界的推导过程同粘性边界相类似，在假设边界上不存在能量反射前提下，基于二维散射波为柱面波的情形可推导出任一半径γb处，以γb为外法线的微元面上应力同该处速度和位移的关系为：其中，G为剪切模量;ρ为介质密度;cs为介质中的剪切波速。

由式(1)可以看出，如果在半径rb处截断介质，并且在截断边界处施加等效的物理元件就可以消除波在人工边界处的反射。

由公式可知施加的物理元件为一个弹簧和一个阻尼器。

对于平面内波动问题，在人工边界的切线和法线两个方向上均需施加弹簧阻尼器，法线方向上的弹簧阻尼器值应从理论上重新推导，但可以将G和cs 简单地用E和cp替换。

ANSYS 粘弹性材料1.1 ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分，在载荷作用下弹性部分是即时响应的，而粘性部分需要经过一段时间才能表现出来。

一般的，应力函数是由积分形式给出的，在小应变理论下，各向同性的粘弹性本构方程可以写成如下形式：()()002t t de d G t d I K t d d d σττττττ∆=-+-⎰⎰ (1) 其中σ＝Cauchy 应力()G t ＝为剪切松弛核函数()K t ＝为体积松弛核函数e ＝为应变偏量部分（剪切变形）∆＝为应变体积部分（体积变形）t ＝当前时间τ＝过去时间I ＝为单位张量。

该式是根据松弛条件本构方程(1)，通过将一点的应变分解为应变球张量（体积变形）和应变斜张量（剪切变形）两部分，推导而得的。

这里不再敖述，可参考相关文献等。

ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种，一种是广义Maxwell 单元（VISCO88 和 VISCO89）所采用的Maxwell 形式，一种是结构单元所采用的Prony 级数形式。

实际上，这两种表示方式是一致的，只是具体数学表达式有一点点不同。

1.2 Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为：()1exp G n i G i it G t G G τ∞=⎛⎫=+- ⎪⎝⎭∑ (2) ()1exp K n i K i i t K t K K τ∞=⎛⎫=+- ⎪⎝⎭∑ (3)其中，G ∞和i G 是剪切模量，K ∞和i K 是体积模量，G i τ和Ki τ是各Prony 级数分量的松弛时间(Relative time)。

再定义下面相对模量(Relative modulus) 0G i i G G α= (4)0K i i K K α= (5)其中，0G ，0K 分别为粘弹性材质的瞬态模量，并定义式如下：()010Gn i i G G t G G ∞====+∑ (6)()010Kn i i K K t K K ∞====+∑ (7)在ANSYS 中，Prony 级数的阶数G n 和K n 可以不必相同，当然其中的松弛时间G i τ和K i τ也不必相同。