当前位置：文档之家 › 材料力学(金忠谋)第六版答案第06章.doc

材料力学(金忠谋)第六版答案第06章.doc

  • 格式：doc
  • 大小：943.50 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

材料力学(金忠谋)第六版课后习题及答案

材料力学(金忠谋)第六版课后习题及答案

解
（1） ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示，各杆材料皆为铸铁，许用拉应力[σ +]=400kg/cm2， 许用压应力[σ − ]=600kg/cm2，各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示，柱的横截面为边长20cm的正方形，材料服从虎克定律，其
弹性模量 E = 0.10 ×105 MPa．如不计柱自重，试求：
（1） （2） （3） （4）
作轴力图； 各段柱横截面上的应力； 各段柱的纵向线应变； 柱的总变形．
解：
（1） 轴力图
（2） AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
（3） AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力，大小为 Τ1 =
Ρ 2
DC 杆受压力，大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg

金属材料及热处理第六版习题册答案解析

金属材料及热处理第六版习题册答案解析

金属材料与热处理习题册答案绪论一、填空题1、成分、组织、热处理、性能之间。

2、石器时代、青铜器时代、铁器时代、钢铁时代、人工合成材料时代。

3、成分、热处理、性能、性能。

二、选择题：1、A2、B3、C三、简答题1、掌握金属材料与热处理的相关知识对机械加工有什么现实意义？答：机械工人所使用的工具、刀夹、量具以及加工的零件大都是金属材料，所以了解金属材料与热处理后相关知识，对我们工作中正确合理地使用这些工具，根据材料特点正确合理地选择和刃磨刀具几何参数；选择适当的切削用量；正确选择改善零件工艺必能的方法都具有非常的现实意义。

2、如何学好《金属材料与热热处理》这门课程？答：在学习过程中，只要认真掌握重要的概念和基本理论，按照材料的成分和热处理决定组织，组织决定其性能，性能又决定其用途这一内在关系进行学习和记忆；注意理论联系实际，认真完成作业和实验等教学环节，是完全可以学好这门课程的。

第一章金属的结构和结晶1-1金属的晶体结构一、填空题1、非晶体晶体晶体2、体心立方面心立方密排立方体心立方面心立方密排立方3、晶体缺陷点缺陷面缺陷二、判断题1、√2、√3、×4、√三、选择题1、A2、C3、C四、名词解释1、晶格与晶胞：P5答：将原子简化为一个质点，再用假想的线将它们连接起来，这样就形成了一个能反映原子排列规律的空间格架，称为晶格；晶胞是能够完整地反映晶体晶格特征的最小几何单元。

3、单晶体与多晶体答：只由一个晶粒组成称为单晶格，多晶格是由很多大小，外形和晶格排列方向均不相同的小晶格组成的。

五、简答题书P6□1-2纯金属的结晶一、填空题1、液体状态固体状态2、过冷度3、冷却速度冷却速度4、晶核的产生长大5、强度硬度塑性二、判断题1、×2、×3、×4、×5、√6、√三、选择题1、C、B、A2、B3、A4、A四、名词解释1、结晶与结晶潜热 (P8)答：（1）结晶：是金属从高温液体状态，冷却凝固为原子有序排列的固体状态的过程。

材料力学(金忠谋)第六版答案-附录

材料力学(金忠谋)第六版答案-附录

材料力学(金忠谋)第六版答案-附录附录I 截面图形的几何性质I-1 求下列截面图形对z 轴的静矩与形心的位置。

解：（a ）)2)2((2)2(2h t h b t h ht t h bt s z ++=⋅++=hb h t h b h b t h t h b t A s y zc +++=+++==2)2()()2)2((22（b ）322332219211)}2)4()43()41()43(32(])4()43[(2{4442DD D D D D D D D D s z =--⨯-+⨯⨯-=ππDD D D D DAs y z c 1367.0])2()43[(2)44(219211223=-⨯+⨯==π（c ）]22)[(22)(2h t t b t h ht t t t b s z +⋅-=⨯+⨯⨯-=tb)(2)(2t b h h t t b A s y z c -++-==I-2 试求（1）图示工字形截面对形心轴 y 及 z 的惯性矩zI 与I y 。

（2）图示 T 字形截面对形心轴的惯矩zI 与I y 。

解(a)12)2)((12)2)((123333t h t b bh t h t b bh J z ---=---=12))2(2(12))(2(1222333t t h b t t t h tb J y -+=-+=(b) cmy c 643.9)520515(2)515(552522=⨯+⨯-⨯+⨯=(b433423231615121551252010186520)643.91025(12205515)5.2643.9(12515cm J cm J y z =⨯+⨯==⨯⨯--+⨯+⨯⋅-+⨯=I-3 求图示椭圆截面对长轴的惯矩、惯性半径与对形心的极惯矩。

解：θθcos ,sin ⋅=⋅=a z b yθθd b dy cos = ⎰⎰--⋅==∴b bbbz zdyy dA y J 222322223224cos sin 2cos cos sin 2ab d abd b a b J bb z πθθθθθθθππ==⋅=⎰⎰--)(4)(42422333b a ab b a ab J J J b ab ab AJ i y z p zz +=+=+====ππππI-4 试求图示的41的圆面积（半径a ）对于z ，yyy 轴的惯性积zyI 。

材料力学(金忠谋)第六版完整版问题详解

材料力学(金忠谋)第六版完整版问题详解

第一章 绪论1-1 求图示杆在各截面（I ）、（II ）、（III ）上的力，并说明它的性质．解：（a ）I-I 截面： N = 20KN (拉)II-II 截面： N = -10KN （压）III-III 截面： N = -50KN (压)（b ）I-I 截面： N = 40KN （拉）II-II 截面： N = 10KN (拉)III-III 截面： N = 20KN （拉）1-2 已知P 、M 0、l 、a ，分别求山下列图示各杆指定截面（I ）、(II)上的力解：（a ）：（I ）截面：力为零。

（II ）截面：M = Pa （弯矩）Q = -P （剪力）（b ）：（I ）截面：θsin 31P Q =θsin 61PL M = （II ）截面：θsin 32P Q = θsin 92PL M =（c ）：（I ）截面：L M Q 0-= 021M M = （II ）截面：L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙，试求（1）支座反力，（2）1-1、2-２、3-3各横截面上的力（1-1，2-2是无限接近集中力偶作用点．）解：10110=⨯=A Y （KN ）1055.110-=+⨯-=A M （KN-M ）（1-1） 截面：10110=⨯=Q （KN ）521110-=⨯⨯-=M （KN-M ） （2-2）截面：10=Q （KN ）055=-=M （KN-M ）（2-3）截面：10=Q （KN ）551110-=+⨯⨯-=M （KN-M ）1-4 求图示挂钩AB 在截面 1-1、2-2上的力．解：（1-1）截面：P N 32=a P M ⋅=43 （2-2）截面：P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座，B 端用拉杆约束住，求拉杆的力和在梁1-1截面上的力．解：（1）拉杆力T ：1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT （KN ）（拉） （2）（1-1）截面力：Q 、N 、M ：5030sin -=-=οT Q （KN ）6.8630cos -=-=οT N （KN ）（压）()2550.030sin =⨯=οT M （KN-M ）1-6 一重物 P ＝10 kN 由均质杆 AB 及绳索 CD 支持如图示，杆的自重不计。

材料力学(金忠谋)第六版完整编辑版规范标准答案

材料力学(金忠谋)第六版完整编辑版规范标准答案
1-2已知P、M0、l、a，分别求山下列图示各杆指定截面（I）、(II)上的内力
解：（a）：（I）截面：内力为零。
（II）截面：M = Pa（弯矩）
Q = -P（剪力）
（b）：（I）截面：
（II）截面：
（c）：（I）截面：
（II）截面：
1-3图示AB梁之左端固定在墙内，试求（1）支座反力，（2）1-1、2-２、3-3各横截面上的内力（1-1，2-2是无限接近集中力偶作用点．）
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中，杆（1）是铸铁的，E1=120Gpa， ＝80MPa；杆（2）是铜的，EA＝100GPa， ＝60Gpa；杆（3）是钢的，EA＝200GPa， =120Mpa。载荷P＝160kN，设A1：A2：A3=2：２：１，试确定各杆的截面积。
解:
各杆的应力关系为
解
（1）
(2)
2-11铰接的正方形结构如图所示，各杆材料皆为铸铁，许用拉应力[ +]=400kg/cm2，许用压应力[ ]=600kg/cm2，各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力，大小为
DC杆受压力，大小为
得
得
故
2-12图示拉杆沿斜截面m－n由两部分胶合而成，设在胶合面上许用拉应力[ ]＝100MPa，许用剪应力 =50MPa，胶合面的强度控制杆件的拉力，试求：为使杆件承受最大拉力P， 角的值应为多少？若横截面面积为4cm2，并规定 ，试确定许可载荷P。
解:
只计P时，有
只计2P时，有
且有
联立，解得
(方向水平向左) (方向水平向右)
（b）

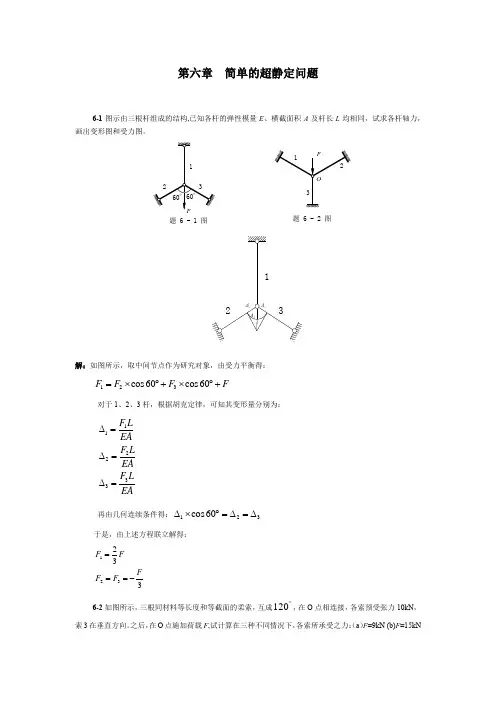
家电公司研发部资料材料力学习题答案(六)

家电公司研发部资料材料力学习题答案(六)

第六章 简单的超静定问题6-1图示由三根杆组成的结构,已知各杆的弹性模量E 、横截面积A 及杆长L 均相同，试求各杆轴力，画出变形图和受力图。

123Δ2Δ3Δ1解：如图所示，取中间节点作为研究对象，由受力平衡得：123cos60cos60F F F F =⨯︒+⨯︒+对于1、2、3杆，根据胡克定律，可知其变形量分别为：112233F L EA F L EA F L EA ∆=∆=∆=再由几何连续条件得：123cos60∆⨯︒=∆=∆于是，由上述方程联立解得：123233F F FF F ===-6-2如图所示，三根同材料等长度和等截面的柔索，互成︒120，在O 点相连接，各索预受张力10kN ，索3在垂直方向。

之后，在O 点施加荷载F ,试计算在三种不同情况下，各索所承受之力：（a ）F =9kN (b)F =15kN题 6 - 1 图题 6 - 2 图(c)F =21kN 。

答：（a ）F =9kN 时，12313,4N N kN N kN ===（b ）F =15kN 时，12315,0N N kN N ===（c ）F =21kN 时，12321,0N N kN N === 解：首先计算当绳索3刚好无拉力时荷载F 的值。

如图所示，取节点O 作为研究对象。

由于绳索上实现施加了10KN 的拉力，因此由节点的竖向平衡可知：12cos60cos60F F F =⨯︒+⨯︒则F=10KN(1)由于F=9KN<10KN (不太明白怎么做)于是绳索3中仍然有拉力。

……(2)由于F=15KN>10KN 于是绳索3中没有拉力。

因此由节点的竖向平衡可知：12cos60cos60F F F =⨯︒+⨯︒则123150F F KN F KN===(3)由于F=21KN>10KN 于是绳索3中没有拉力。

因此由节点的竖向平衡可知：12cos60cos60F F F =⨯︒+⨯︒则123210F F KN F KN===6-3图示对称结构中，杆BC 为刚性杆，其余四根杆的EA 均相同，试求荷载F 作用下四根杆的轴力。

材料力学金忠谋第六版答案第章

材料力学金忠谋第六版答案第章
解：
(a) (b)
(c )(d)
(e)
8-6已知矩形截面梁某截面上的弯矩和剪力分别为M＝10kN·m，FS＝120kN，试绘出截面上1、2、3、4各点单元体的应力状态，并求其主应力。
解：
8-7在棱柱形单元体的AB面上以及与ABC面平行的前后面上（与纸平面平行的面），均无应力作用。在AC面和BC面上的正应力均为-15MPa，试求AC和BC面上的剪应力与此单元体主应力的大小和方向。
解：(a)
(b)
(c)
(d)
8-12直径d＝2cm的受扭圆轴，今测得与轴线成 方向的线应变 。已知E＝200GPa， =，试求扭转力矩 。
解：
8-13一个No28a工字钢梁，受力如图所示，今测得在梁的中性层上K点、与轴线成 方向上的线应变 。已知E＝200GPa， =。试求此时梁承受的载荷P。
解： :
解：
8-22图示半径为 ，厚度为t的圆板，在周边受径向均有载荷q作用，试求圆板厚度变化量 及体积应变 。
解：
（1）
(2)
解：
所以三个主应力：
8-10在一块厚钢块上挖了一条贯穿的槽，槽的宽度和深度都是1cm。在此槽内紧密无隙地嵌入了一铝质立方块，其尺寸是111cm，并受P＝6kN压缩力如图示，试求铝立方块的三个主应力。假定厚钢块是不变形的，铝的E=71GPa， ＝。
解
8-11已知单元体的应力圆如图所示（应力单位：MPa）。试作出主单元体的受力图，并指出与应力圆上A点相对应的截面位置（在主单元体图上标出）。
解：(a)
（与 方向夹角）
(b)
（与 方向夹角）或 （与水平方向交角）
(c)
（与 方向夹角）
(d)
8-4单元体各面的应力如图示（应力单位为MPa），试用解析法和图解法计算主应力的大小及所在截面的方位，并在单元体内注明。

材料力学课后习题答案6章

材料力学课后习题答案6章

由切应力互等定理可知，纵截面上的切应力 τ x 与 τ 2max 一样大。 左、右端面上弯曲正应力构成的轴向合力分别为
Fx1 =
bh Fa 1 σ1max ( ) = 2 2 2h bh Fa 1 Fx 2 = σ 2max ( ) = h 2 2
左、右端面上弯曲切应力构成的竖向合力大小相等，其值为
(也可用左侧题号书签直接查找题目与解)
6-3
图示带传动装置，胶带的横截面为梯形，截面形心至上、下边缘的距离分别为
y1 与 y2，材料的弹性模量为 E。试求胶带内的最大弯曲拉应力与最大弯曲压应力。
题 6-3 图 解：由题图可见，胶带中性层的最小曲率半径为
ρmin = R1
依据
σ=
Ey ρ
可得胶带内的最大弯曲拉应力和最大弯曲压应力分别为
Fy 1 = F y 2 =
1ห้องสมุดไป่ตู้F 6
Fa 2h
顺便指出，纵截面上弯曲切应力构成的轴向合力为
FSx = τ x ( ab) =
3．检查单元体的平衡方程是否满足
∑F ∑F
x
= 0，Fx 2 − Fx1 − FSx = = 0，Fy1 − Fy 2
y
Fa Fa Fa − − =0 h 2 h 2h F F = − =0 6 6
题 6-10 图 解：1.查№18 工字钢的有关数据 工字钢截面大致形状及尺寸符号示如图 6-10。
图 6-10 由附录 F 表 4 查得
h = 180mm，b = 94mm t = 10.7mm，I z = 1660cm 4，Wz = 185cm 3
2．计算顶边 AB 的长度改变量 顶边处有
3
σ max =
计算中用到 h1 = h / 2 − t = 79.3mm。

材料力学第六章重点解析

材料力学第六章重点解析

本章基本要求：• 1. 熟练掌握梁的变形计算。

• 2. 熟练掌握弯曲刚度的计算。

•3. 熟练掌握简单超静定梁的计算。

•本章研究：• 1. 二重积分法求弯曲变形。

• 2. 叠加法求弯曲变形。

• 3. 弯曲刚度条件。

•4. 变形比较法求超静定梁。

第六章弯曲变形§6-1 工程中的弯曲变形问题一. 挠曲线、挠度与转角1 . 挠曲线：变形后梁的轴线成为一个光滑、连续的在xy 平面内的曲线称之。

挠曲线方程：w = f （x ）—亦称弹性曲线方程。

§6-2 挠曲线的微分方程xy③式为挠曲线的近似┄┄③微分方程。

Arrayx••AθBθmaxw()p ΛΛΛΛ)M ’F s ’F sM w c2•••aLaF a L F a F 12231+-M ’F sM w c22BFθaBF 2θBM θaBMθ•••⎫⎛223l qb xqdxdx x qdx•••mm m 0432.010432.4-=⨯-CδBw EN BθBθ确定超静定次数：一次超静定。

(+)(-)qF RBw B =0等效系统w F w q F sql 8535二. 解题步骤1. 确定超静定次数：以确定补充方程数。

2. 取静定基：解除多余约束，以静定系统代替超静定系统。

3. 建立力的等效系统：在静定基上加上多余约束未知力以及原有的外力，使之与原受力系统等效。

4. 建立变形的等效系统：即找变形协调条件。

为了使变形等效，在多余约束未知力作用点上的挠度或转角一般为：w （或θ）= 0 ；或w （或θ）= 常数。

5. 用叠加法求多余约束未知力作用点上的位移w （或θ）。

此方法称为变形比较法。

6. 作弯矩图；求最大正应力。

MA=+=AM Aq A θθθ；F F F F 808.0167135≈=∴F RC F ’RC•••（+）F RC= w c MlF RCEIFl EI Fl w 33max0208.048≈=EIFl EI ql w 34max 013.03845≈=4.缩小跨度，增加或加固支座：l ↓、M ↓3.采用卸载装置：想法将载荷传递给大地或大件物体。

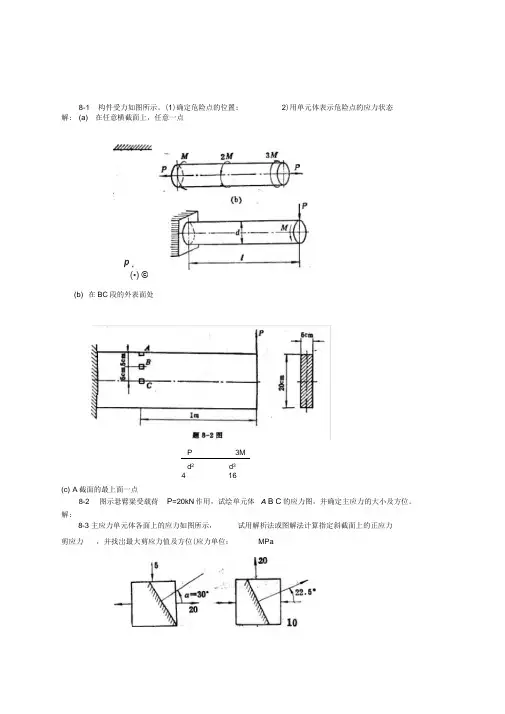
材料力学金忠谋第六版答案第章

材料力学金忠谋第六版答案第章

8-1 构件受力如图所示。

(1)确定危险点的位置; (a) 在任意横截面上，任意一点(•) ©(b) 在BC 段的外表面处p解: 2)用单元体表示危险点的应力状态P 3M d 2d 3416(c) A 截面的最上面一点8-2 图示悬臂粱受载荷 解:P =20kN 作用，试绘单元体 A B C 的应力图，并确定主应力的大小及方位。

8-3 主应力单元体各面上的应力如图所示，试用解析法或图解法计算指定斜截面上的正应力剪应力，并找岀最大剪应力值及方位(应力单位： MPa45° （与140方向夹角）单元体各面的应力如图示（应力单位为MPa ，试用解析法和图解法计算主应力的大小及所在 截面的方位，并在单元体内注明。

解：（a ）（b ）（C ）（d ） 8-5解：⑻1 22 45° (与12COS 2220方向夹角)20 520— COS 60° 13.75MPa2(b)2COS 2201020^COS 135°25.606MPa(c)-2sin2 245°20 10sin 2（与1方向夹角）或135° 135010.606MPa（与水平方向交角）(d)8-4作岀图示单元体的三向应力图，并求岀主应力和最大剪应力，画岀主单元体。

15MPa0;30MPa（方向平行于 AB ）解:⑻(c ) (e)ZE?M= 10kN • m, F S = 120kN ，试绘岀截面上 1、2、3、8-64各点单元体的应力状态，并求其主应力。

解：8-7 在棱柱形单元体的 AB 面上以及与ABC 面平行的前后面上（与纸平面平行的面），均无应力作用。

在AC 面和BC 面上的正应力均为-15MPa ,试求AC 和BC 面上的剪应力与此单元体主应力的大小和方向。

x 0 已知矩形截面梁某截面上的弯矩和剪力分别为解:(d)8-8 某点的应力状态如图所示，已知试参考如何根据已知数据直接作出应力图解：x, y面上无故为主应力2, 3，所以可以直接作应力圆l.OOQlEa■ K!8-9 每边均为icm的钢质立方体，放在边长均为的刚性方槽内，立方体顶上承受总压力材料的E= 200GPa, 试求钢质立方体内三个主应力之值。

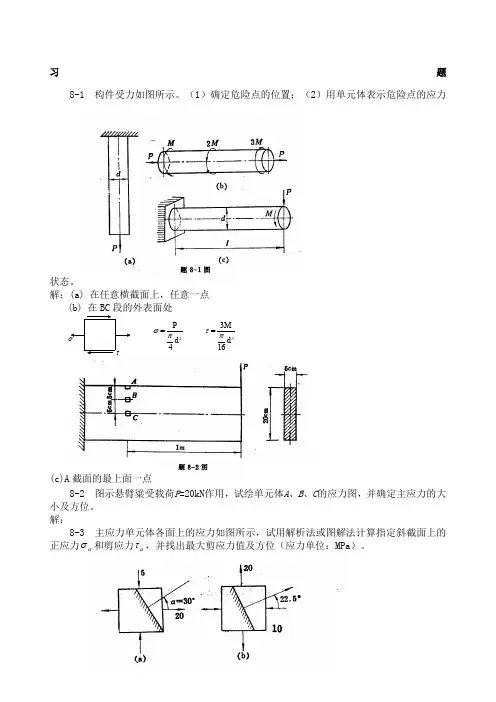
材料力学金忠谋第六版答案第章

材料力学金忠谋第六版答案第章

习 题8-1 构件受力如图所示。

（1）确定危险点的位置；（2）用单元体表示危险点的应力状态。

解：(a) 在任意横截面上，任意一点(b) 在BC 段的外表面处 24P d σπ=3316M dτπ=(c)A 截面的最上面一点8-2 图示悬臂粱受载荷P =20kN 作用，试绘单元体A 、B 、C 的应力图，并确定主应力的大小及方位。

解：8-3 主应力单元体各面上的应力如图所示，试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ，并找出最大剪应力值及方位（应力单位：MPa ）。

解：(a) ()()1212205205cos 2cos 6013.752222MPa ασσσσσα+---+-=+=+= 45α= （与120σ=方向夹角） (b)()()()121220102010cos 2cos 135 5.6062222MPa ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=- 45α= （与1σ方向夹角）或135（与水平方向交角） (c)45α= （与140σ=方向夹角）(d)8-4 单元体各面的应力如图示（应力单位为MPa ），试用解析法和图解法计算主应力的大小及所在截面的方位，并在单元体内注明。

解：(a)(b)(c)(d)8-5 作出图示单元体的三向应力图，并求出主应力和最大剪应力，画出主单元体。

解：(a) (b)(c ) (d)(e)8-6 已知矩形截面梁某截面上的弯矩和剪力分别为M ＝10kN ·m ，F S ＝120kN ，试绘出截面上1、2、3、4各点单元体的应力状态，并求其主应力。

解：8-7 在棱柱形单元体的AB 面上以及与ABC 面平行的前后面上（与纸平面平行的面），均无应力作用。

在AC 面和BC 面上的正应力均为-15MPa ，试求AC 和BC 面上的剪应力与此单元体主应力的大小和方向。

材力习题册(第六版)参考答案(1-3章)

材力习题册(第六版)参考答案(1-3章)

D
)
2．轴向拉伸细长杆件如图 2 所示，其中 1-1 面靠近集中力作用的左端面，则正确的说法 A．1-1、2-2 面上应力皆均匀分布 B．1-1、2-2 面上应力皆非均匀分布 C．1-1 面上应力非均匀分布， 2-2 面上应力均匀分布 D．1-1 面上应力均匀分布， 2-2 面上应力非均匀分布
（图 B 端 D 任意点 A ) B 都是横截面 D 都是 45 斜截面
0 0
14. 轴向拉伸杆，正应力最大的截面和剪应力最大的截面 (
15. 设轴向拉伸杆横截面上的正应力为 σ ，则 45 斜截面上的正应力和剪应力 ( D )。 B 均为 σ D 均为 σ /2 C δ 和ψ D σ s、 δ 和 ψ
17. 由拉压变形公式 l A C A C
F l FN l 即 E N 可知，弹性模量 ( A )。 A l EA
B 与载荷成正比 D 与横截面面积成正比
与载荷、杆长、横截面面积无关 与杆长成正比 A )是正确的。 内力随外力增大而增大 内力随外力增大而减小 C B D
18. 在下列说法，(
B 内力与外力无关 D 内力沿杆轴不变 ) 。 σ ＞300MPa σ ＜200MPa B ） 。 B. 剪切面面积为 bh,挤压面面积为 bc； D. 剪切面面积为 bh,挤压面面积为 ch。 C ） ，计算挤压面积
19. 一拉伸钢杆，弹性模量 E＝200GPa，比例极限为 200MPa，今测得其轴向应变 ε ＝ 0.0015，则横截面上的正应力 ( A C σ ＝Eε ＝300MPa 200MPa＜σ ＜300Mpa
= －2(arctan
)=2.5×
rad
2．试求图示结构 m m 和 n n 两截面的内
-2-

材料力学答案第六章

材料力学答案第六章

第六章答案第六章弯曲应力6.1钢丝直径d=0.4mm,弹性模量E=200GPa,若将钢丝弯成直径 D=400mm 的圆弧时，试求钢丝横截面上的最大弯曲正应力。

（200MPa ）解：钢丝的弯矩和中性层曲率半径之间的关系为： 则：心旦，由弯曲正应力公式得f 二如=荃，钢丝弯成圆弧后，产生的弯E(2) rr —J —Ed 3200 100.4 -200MPakJ——200 MPa -maxDD40026.2矩形截面梁如图所示。

b ==8cm, h =12cm, 试求危险截面上(20.8MPa, 10.4MPa, 0) 解：由平衡方程1得到：F A 二 F B =丄 2 4 =4KN2危险截面在梁的中点处：1 2 1 2 M max ql2 4 4KNm 8 8 11 I z =b h 2=80 1203 =1152 10412126.3从直径为d 的圆木中截取一矩形截面梁，试根据强度曲变形，其中性层的曲率半径D d D------------ &——2 2mm 44KN观点求出所截取的矩形截面的最合理的高h 和宽b 。

4KNma 、c 、d 三点的弯曲正应力。

(h= -d , b=」d)3 3机械解：最大弯曲正应力:max-max一y max-max土木W z4KNm系数：1 2 1 2 2 1 2 3 W=1bh二b(d _b)=1(db_b)dW dt d2 -3b2h/b的最佳值应应使梁的抗弯截面系数为最大。

抗弯截面为b为自变量的函数。

6.4图示两根简支梁，其跨度、荷载及截面面积都相同。

一个是整体截面梁，另一个是由两 根方木叠置而成(二方木之间不加任何联1 3 1 3 8 4bh 3 150 2003 = 108 mm 412 12再有矩形截面梁的弯曲正应力弯曲正应力为L.T-10MP a ，许用剪应力为• ‘ = 1MPa , 试求许可荷载P 。

(P=8.1kN )解：依题给条件，对梁进行受力分析，由平衡条件，列平衡方程，做出剪力图 和弯矩图如右所示 (1)按木材弯曲正应力强度要求确定许可荷载F s S ； T = -----------------I z b ，故 9 =0, aF S240 1033 __ 2.0 A 2 150 200MPaF S S ZI z b 40 103 5.625 105108 150= 1.5 MPa6.6图示简支梁由三块木板胶合而成， l=1m,胶缝的许用剪应力为!. l-0.5MPa木材的许用系)，试画出沿截面高度的弯曲正应力分布 图，并分别计算梁中的最大弯曲正应力。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

弯曲应力6-1 求图示各梁在m－m截面上A点的正应力和危险截面上最大正应力。

题6-1图解：（a）mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ（压）MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ（b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。

解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。

试求梁内最大拉应力与最大压应力。

已知I z =10170cm 4，h 1=9.65cm ，h 2=15.35cm 。

解：A 截面：Mpa 95.371065.9101017010402831max =⨯⨯⨯⨯=--σ （拉）Mpa 37.501035.15101017010402831min -=⨯⨯⨯⨯-=--σ（压） E 截面Mpa 19.301035.15101017010202832max =⨯⨯⨯⨯=--σ （拉）Mpa 98.181065.9101017010202832min -=⨯⨯⨯⨯-=--σ （压） 6-4 一根直径为d 的钢丝绕于直径为D 的圆轴上。

（1） 求钢丝由于弯曲而产生的最大弯曲正应力（设钢丝处于弹性状态）（2） 若 d ＝lmm ，材料的屈服极限s σ=700MPa ，弹性模量E =210GPa ，求不使钢丝产生残余变形的轴径D 。

解：EJM =ρ1Dd E EJ M 324πρ== D d E d M W M ⋅===3max 32πσ cm m dE D s 303.01070010110210639==⨯⨯⨯⨯=⋅≥-σ6-5 矩形悬臂梁如图示．已知l = 4 m ，32=h b ，q =10kN/m ，许用应力[σ]=10Mpa 。

试确定此梁横截面尺寸。

解：m KN ql M ⋅=⨯⨯==80410212122max 963266322h h h h W =⨯== 910101080263h M W W M =⨯⨯==⇒=σσ cm m h 6.41416.0==cm b 7.27=6-6 20a 工字钢梁的支承和受力情况如图所示。

若[σ]＝160MPa ，试求许用载荷P 。

解：3237cm W = P 32 m KN P M ⋅=32max[][]P W M 32102371016066=⨯⨯⨯=⋅=-σ （M 图） P 32 []KN P 880.5623716023=⨯⨯= 6-7 压板的尺寸和载荷情况如图所示。

材料为 45钢，s σ＝380 MPa ，取安全系数5.1=n 。

试校核压板强度。

解：2331568)121230122030(101mm W =⨯-⨯⨯= m N M ⋅=⨯⨯⨯=-3601020101833[]σσ<=⨯==-MPa W M 6.2291015683609 6-8 由两个槽钢组成的梁受力如图示。

已知材料的许用应力[σ]＝150 MPa ，试选择槽钢号码。

解：m KN M ⋅=60max[]33363m ax400104.010*******cm m MW x =⨯=⨯⨯==-σ查表：（22a ， 332006.217cm cm W x >=）m KN ⋅60（ M 图）6-9 割刀在切割工件时，受到P ＝1kN 的切销力的作用。

割刀尺寸如图所示。

试求割刀内最大弯曲应力。

解：m N p M ⋅=⨯⨯=-I 81083m N p M ⋅=⨯⨯=-∏30103033242.706135.2mm W =⨯=I321506154mm W =⨯=∏()MPa W M 114104.7089m ax =⨯==-I I I σ()MPa W M 20010150309m ax =⨯==-∏∏∏σ6-10 图示圆木，直径为D ，需要从中切取一矩形截面梁。

试问（1）如要使所切矩形截面的抗弯强度最高，h 、b 分别为何值？（2）如要使所切矩形截面的抗弯刚度最高，h 、b 又分别为何值？解：6)(6222b D b bh W -== 0=dbdW ∴ 06322=-b D ∴322D b = 2222323D D D h =-= ∴从强度讲：D b 57735.0=∴ D h 8165.0=12)(123222b D b bh J -== 0=dbdJ 0)2()(23)(21222322=-⨯-⨯⨯+-b b D b b D ∴从刚度讲 D b 50.0=D h 866.0=6－11 T 字形截面的铸铁梁受纯弯曲如图示，欲使其最大压应力为最大拉应力的3倍，巳知h = 12cm ，t =3cm ，试确定其翼板宽度b 之值。

解：3max max ＝下上拉压y y =σσ 下上＝y y 312=h y y ＝＋下上cm y 3412＝＝下 05.4)39()233)(3(=⨯⨯--⨯=b S cm b 275.135.439=⨯⨯⨯= 6-12 图示简支梁，由No.18工字钢制成，在外载荷作用下，测得横截面A 处梁底面的纵向正应变4100.3-⨯=ε，试计算梁的最大弯曲正应力σmax 。

已知钢的弹性模量E =200GPa, a =1m 。

解：MPa E A 60100.31020049=⨯⨯⨯==-εσ 28/34/3max max ===A A M M σσ MPa A 1206022max =⨯==σσ243qa 283qa24qa （M 图）6-13 试计算图示矩形截面简支梁的1-1面上a 点和b 点的正应力和剪应力。

解：1－1截面KN Q 6364.3=m KN M ⋅=6364.3433375.210912155.712cm bh J =⨯== 283105.310375.2109106364.3--⨯⨯⨯⨯==y J M a σ MPa 03.6=82310375.2109105.7106364.3--⨯⨯⨯⨯=b σ MPa 93.12=2863105.710375.2109105.5)5.74(106364.3---⨯⨯⨯⨯⨯⨯⨯⨯==Jb QS a τ MPa 379.0=6-14 计算在均布载荷 q ＝10 kN ／m 作用下，圆截面简支梁的最大正应力和最大剪应力，并指出它们发生在何处。

解：232max 110108181⨯⨯⨯==ql M m N ⋅⨯=31025.11101021213max ⨯⨯⨯==ql Q N 3105⨯=633m ax 105321025.1-⨯⨯⨯==πσW M MPa 86.101= 在跨中点上、下边缘34105410534423max ⨯⨯⨯⨯=⨯=-πτA QMPa 46.25= 在梁端，中性轴上6-15 试计算6-12题工字钢简支梁在图示载荷下梁内的最大剪应力。

解： MPa Wqa 60832= qa 41 3185cm W =KN q 6.29123810185106066=⨯⨯⨯⨯⨯=- qa 43 KN qa Q 2.2216.294343max =⨯⨯==（Q 图） MPa Jt QS 12.22105.6104.15102.22323max =⨯⨯⨯⨯==--τ 6-16 矩形截面木梁所受载荷如图示，材料的许用应力[σ]=10Mpa 。

试选择该梁的截面尺寸，设1:2:=b hKN 19 KN 8KN 9KN 1（Q 图） （ M 图）解：KN R A 19= KN R B 29=126132h bh W == []σσ≤⨯==12101433m ax h W M cm m h 6.25256.01010121014363==⨯⨯⨯=cm b 8.12=[]ττ<=⨯⨯⨯⨯==-MPa A Q 961.0106.258.1210215.15.143max 6-17 试为图示外伸梁选择一工字形截面，材料的许用应力[σ]= 160MPa ，[τ]＝80Mpa 。

解：[]3612510160100020cm MW =⨯⨯==σ 取16I ， 3141cm W =)(8.13:cm S J =[]ττ<=⨯⨯⨯==-MPa Jt QS 181.01068.13101533故 取No16工字钢)(x Q KN 15 )(x M m KN ⋅20KN 5 m KN ⋅10KN 10（Q 图） （M 图）6-18 图示起重机安装在两根工字形钢梁上，试求起重机在移动时的最危险位置及所采用工字型钢的号码。

已知 l ＝10 m ，a ＝4 m ，d =2 m 。

起重机的重量 W ＝50 kN ，起重机的吊重P =10 kN ，钢梁材料的许用应力［σ］=160 MPa ，[τ]= 100Mpa 。

解：轻压：KN 10 ，KN 50[]x x x R 658)8(10)10(50101-=-+-= x x Rx x M ⋅-==)658()(0=dxdM 01258=-x m x 833.4= m KN M ⋅=⨯⨯-=17.140833.4)833.4658(max[]63m ax 101601017.140⨯⨯==σM W 33387610876.0cm m =⨯=-取 两个 a I 28 33438215.508cm W cm W z =>=KN 10 KN 50dm 106-19 等腰梯形截面梁，其截面高度为h 。

用应变仪测得其上边的纵向线应变611042-⨯-=ε，下边的纵向线应变621014-⨯=ε。